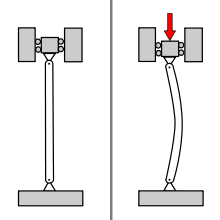
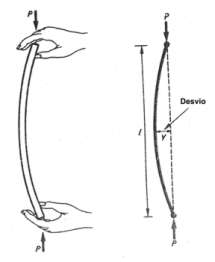
Le flambage ou flambement est un phénomène d'instabilité d'une structure qui, soumise à un effort normal de compression, a tendance à fléchir et se déformer dans une direction perpendiculaire à l'axe de compression (passage d'un état de compression à un état de flexion).
Le terme flambement est plutôt utilisé en mécanique des structures.
Résistance des matériaux
Exemple d'une règle plate:
Si les extrémités de la règle sont tenues et tirées, la rupture de la règle se produit quand les contraintes de traction deviennent supérieures à la résistance mécanique en traction du plastique.
En revanche, si les extrémités de la règle sont tenues et comprimées dans le sens de la longueur, la règle va se plier et se briser avec un effort de compression bien plus faible que celui nécessaire à la rupture en traction.
Ce phénomène est appelé flambage.
En résistance des matériaux (RDM), le flambage est un phénomène d'instabilité élastique mis en évidence lorsqu'une poutre est comprimée ; il se développe un moment de flexion parasite amplifié par les déformations et déplacements de la poutre chargée.
Ce phénomène n'est pas mis en évidence par le modèle RDM classique ou théorie des poutres car ce modèle considère que les efforts de calcul s'appliquent sur la structure non déformée (hypothèses de linéarisation externe et des petits déplacements de la mécanique des solides et de la RDM) et non sur la structure déjà en charge et déformée (théorie du second ordre).
Le flambage se produit d'autant plus facilement que la poutre est longue et de faible section. Le flambage dépend aussi du type de liaisons des extrémités de la poutre (les conditions d'appui).
Même si le terme poutre est employé ici, l'hypothèse RDM des petits déplacements doit être abandonnée pour que le modèle soit plus réaliste. Le modèle RDM doit être complété avec les hypothèses supplémentaires que les déformations restent petites mais que les déplacements peuvent être grands ; cela permet de prendre en compte les phénomènes du second ordre négligés dans le modèle RDM.
Ce modèle RDM complété n'est plus linéaire, la résolution se fait par itérations successives jusqu'à convergence éventuelle du résultat. Ce modèle met en évidence des instabilités dont la charge critique d'Euler est un exemple simple.
Comme cette formule ne fait intervenir que des termes issus du modèle RDM élastique linéaire (module d'Young et géométrie de la poutre), on dit alors que le flambement est un phénomène d'instabilité élastique. En général le flambement élastique n'est que le début d'un comportement non linéaire bien plus complexe qui une fois amorcé conduit à des déformations plastiques dans le matériau puis à la ruine de la poutre.
Pour une poutre d'inertie constante soumise à un effort normal de compression simple, la charge critique de flambage théorique est donnée par la formule d'Euler:
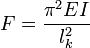
où
est le module d'Young du matériau ;
est le moment quadratique de la poutre ;
est la longueur de flambement de la poutre.
Cette charge critique est évidemment limitée par la résistance en section de la poutre (à partir d'un certain élancement, la ruine est atteinte avant l'apparition du flambage). Dans le cas réel, la ruine par flambage est atteinte encore plus précocement en raison notamment des imperfections de production et de mise en œuvre (voir ci-dessous).
Le facteur 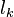 représente une longueur équivalente à celle d'une poutre rotulée-rotulée. Il s'agit de la distance séparant deux points d'inflexion de la déformée de la poutre soit la distance entre deux points de moment de flexion nul. Ainsi,
représente une longueur équivalente à celle d'une poutre rotulée-rotulée. Il s'agit de la distance séparant deux points d'inflexion de la déformée de la poutre soit la distance entre deux points de moment de flexion nul. Ainsi,
pour une poutre rotulée aux deux bouts, , la longueur de la poutre ;
pour une poutre encastrée - encastrée mobile (selon l'axe vertical), ;
pour une poutre encastrée-rotulée, (le coefficient 0,699 est une approximation) ;
pour une poutre encastrée-libre, .
Le flambage est un phénomène d'instabilité élastique lié au module d'Young et indépendant de la limite d'élasticité, utiliser un acier de limite d'élasticité supérieure pour diminuer le flambage est une erreur grave.
: 2 forces de compression opposées exercées suivant l’axe horizontal de la poutre à ses extrémités ;
L'axe vertical ;
: la ligne déformée de la poutre, appelée aussi « déformée » ;
: le moment de flexion dans la poutre à l’abscisse x ;
: la dérivée par rapport à x de la « déformée » ;
: la dérivée seconde par rapport à x de la « déformée » ;
Si , alors la solution de l'équation différentielle est , pour tout x vérifiant 0 < x < L ; la fonction est la fonction nulle. L'équation de la ligne déformée est y = 0 ; c'est à dire que la poutre est rectiligne. Il n'y a pas de flambement.
C’est donc , ce qui n’est possible que pour avec k = 0 ou -1, +1 ou -2 , +2, etc.
Calcul pratique pour des matériaux homogènes
Ce problème est sérieusement considéré dans les cas du dimensionnement de poteaux ou de piliers et de bielles en mécanique, éléments nécessairement de grande longueur et soumis à la compression.
On définit habituellement un paramètre géométrique 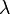 , appelé coefficient d'élancement (sans dimension) :
, appelé coefficient d'élancement (sans dimension) :
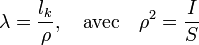
où est le rayon de giration de la poutre et la section de cette poutre.
On peut alors définir un coefficient d'élancement critique 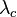 (sans dimension), qui ne dépend que des propriétés du matériau :
(sans dimension), qui ne dépend que des propriétés du matériau :
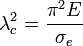
où est la limite d'élasticité du matériau, puis le coefficient d'élancement relatif (sans dimension)
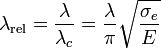
En pratique, la formule d'Euler n'est pas directement utilisée pour dimensionner une poutre. En effet, la charge critique de flambage d'Euler ne pourrait être atteinte que dans le cas idéal d'une barre parfaitement rectiligne et homogène, sans aucune imperfection géométrique et chargée sans aucune excentricité. Dans la réalité, ces imperfections ont pour conséquence de mener à un flambage précoce de la barre, sous-estimé par la formule d'Euler. Enfin, la charge ultime est évidemment bornée par la résistance de la section en compression pure (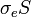 ).
).
Pour tenir compte de manière unifiée de ces différentes considérations, la pratique développée habituellement dans les normes récentes consiste à introduire un facteur de flambage 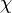 servant à réduire la résistance en section de la barre (compression simple)
servant à réduire la résistance en section de la barre (compression simple) 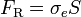 pour arriver à sa résistance globale en compression
pour arriver à sa résistance globale en compression
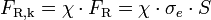 .
.
Ce facteur de flambage, issu de simulations numériques et de résultats expérimentaux, est généralement défini comme suit :
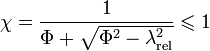
où 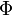 est un facteur défini selon le matériau utilisé et le type d'imperfections. À titre d'exemple, dans la norme suisse de Construction métallique (SIA 263) ce facteur s'écrit :
est un facteur défini selon le matériau utilisé et le type d'imperfections. À titre d'exemple, dans la norme suisse de Construction métallique (SIA 263) ce facteur s'écrit :
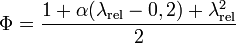
Dans cette formule, 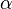 est le facteur d'imperfection du matériau ; il dépend de la direction de flambage considérée et du procédé de fabrication. On remarque que lorsque
est le facteur d'imperfection du matériau ; il dépend de la direction de flambage considérée et du procédé de fabrication. On remarque que lorsque 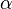 tend vers 0, la courbe de flambage
tend vers 0, la courbe de flambage 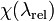 se rapproche de la courbe de flambage d'Euler
se rapproche de la courbe de flambage d'Euler 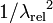 .
.
Lorsque — comme fréquemment — la poutre n'est pas soumise qu'à la compression mais également à la flexion ou à l’effort tranchant, la charge ultime se trouve encore réduite, d'une part car une partie de la résistance est mobilisée pour s'opposer à ces sollicitations, d'autre part car le moment de flexion induit une courbure préalable qui sera amplifiée par la compression. On parle alors d'interaction d'efforts et les critères de rupture sont généralement formulés sur la base de courbes ou formules d'interaction. Ils dépendent notamment des parts relatives des différentes sollicitations dans la sollicitation totale.
Poteaux en béton armé
La formule d'Euler n'est pas applicable aux poteaux et butons en béton armé : en raison de la fissuration du béton, l'inertie varie sur la longueur, ce qui conduit à des calculs complexes. Un des pionniers de ce domaine de calculs fut Pierre Faessel qui établit des abaques de calculs.
Géologie
En géologie, on trouve aussi le phénomène de flambage, mais à une échelle bien plus grande qu'en RDM. La compression d'une masse continentale importante provoque à l'échelle locale ou régionale la formation d'une chaine de montagne. À l'échelle d'un continent entier, le flambage provoque des séries de "creux" et de "bosses" secondaires.
Par exemple, la collision alpine, en Europe occidentale, est responsable de la formation ou réactivation d'autres reliefs secondaires dont l'importance diminue à mesure que l'on s'éloigne des Alpes : Massif central ("bosse") et Limagne ("creux"), la Sologne (creux), le Massif Armoricain et les Alpes Mancelles (Bosse, bien que liée aussi à l'ouverture de l'Atlantique), la Mer du Nord (creux, dont l'autre facteur explicatif est aussi l'ouverture de l'Atlantique), le Pays de Caux et le Pays de Bray (bosses), les marais et polders de la région de Calais et du Nord de la Picardie (creux), le Boulonnais, l'Artois les Ardennes et l'Eifel (Bosses), la Flandre (creux).
On pourrait décrire de la même façon le contrecoup himalayen : plateaux de ***** (creux), Altaï (bosse), lac Baïkal (creux).
挫曲(buckling)也称为屈曲,是一种不稳定的现象,是指细长件在受到压缩力时,因细长件弯曲变形而造成的结构失效。
理论上,挫曲是因为力学平衡方程序的解出现分岔(解的本质发生改变)所造成的。在受力增加到一定程度之后,物体会出现二种平衡状态,一种是纯压缩力,另一个是有侧向偏移变形的平衡状态。
挫曲的特点是在结构件中,边缘承受压缩应力的组件突然断裂,而组件失效时的压应力小于材料可以承受的终极抗压应力。挫曲的数学分析一般会设法加入方向也是轴向,但和轴有一段位移(偏心)的压应力,以产生原来理想施力时不会受现的二次弯矩。
当在一组件(例如杆件)上的压缩负荷增加,多半最后负荷会大到使组件变形不稳定。若负荷继续加大,会造成明显,甚至无法预测的变形,可能让组件完全无法承受负荷。若变形还不是灾难性的,组件仍会继续承受负载。若挫曲的组件是结构件(例如大楼)中的一部份,会由其他的组件来分担已挫曲组件原来要承受的负载。
柱的挫曲
若铁柱的细长比未超过50,视为短的铁柱,若细长比介于50到200之间,是中间长度的铁柱,其特性主要会受材料的强度极限所影响,若细长比超过200,即视为是长的铁柱,其特性主要会受材料的弹性模数影响。
短的水泥柱是指其未支撑长度的细长比小于10的水泥柱,细长比若超过10,即视为是长柱(有时也称为是细长柱)。
木材若细长比小于10,视为是短柱。中间长度木材和长木材的分界不好决定,有一种定义长木材长度下限的方式其长度需大于最小截面的K倍,K会随弹性模数影响以及和平行纤维的最大允许压应力有关,因此会随木材的品种不同而不同,在许多结构工具书中都会列出不同材料的K值。
临界乘载和弹性模数有关,和材料的抗压强度无关。
临界乘载和截面积的截面二次轴矩成正比。
临界乘载明显的受边界支撑条件的影响。边界支撑条件决定挫曲的形式,也决定挫曲时拐点的位置。细长柱变形时的拐点是在其曲率由正变负或由负变正的位置,也是内弯矩为零的位置。

 词典释义:
词典释义:
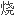
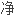 细毛, 燎除细毛
细毛, 燎除细毛
 小鸡的细毛
小鸡的细毛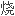 毛
毛 弯曲, 轴线挠度
弯曲, 轴线挠度 ,
, 
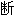 ,
,  切;
切;