En mathématiques, l'enlacement est un nombre entier défini pour deux courbes fermées de l'espace ℝ sans point double. Il décrit la façon dont ces deux courbes sont enlacées, liées l'une par rapport à l'autre. Il fut défini pour la première fois par Gauss.
Si on peut séparer les deux courbes en les déformant sans les couper, alors l'enlacement des deux courbes vaut zéro. La réciproque est fausse.
Calcul de l'enlacement
Il existe plusieurs façons de calculer l'enlacement de deux courbes et . La plus simple consiste à projeter les deux courbes sur un plan en conservant en mémoire à chaque croisement les positions relatives des deux brins (on obtient alors un diagramme de lien. On donne à chaque courbe une orientation (sens de parcours) arbitraire et on considère les croisements d'une courbe avec l'autre, en oubliant les éventuels croisements d'une courbe avec elle-même. On affecte à chaque croisement un indice comme défini ci-dessous (seules ces deux situations sont possibles) :
 |
 |
|
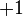 |
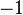 |
Et on définit alors l'enlacement comme la demi-somme des indices de tous les croisement de 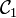 avec
avec 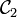 .
.
Si on change l'orientation d'une courbe, le signe de l'enlacement est changé.
Gauss a également montré qu'on peut calculer l'enlacement des deux courbes à partir d'une paramétrisation. Les points de sont parcourus par la fonction lorsque parcourt , avec . On a alors la formule
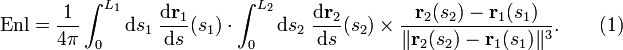
Cette formule se calcule par exemple en considérant que l'une des courbes délimite une surface et que l'autre est parcourue par un courant électrique. On obtient alors le résultat (1) à l'aide des lois de l'électromagnétisme, en calculant le courant passant à travers la surface.
Enlacement d'un ruban
On peut parler de l'enlacement d'un ruban (en) fermé en considérant les deux bords du ruban comme courbes. Dans ce cas, l'enlacement du ruban peut se décomposer en deux termes : l'entortillement de son axe et sa torsade . Le théorème de Călugăreanu-Pohl-White affirme que
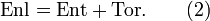
Application en biologie
L'enlacement a été utilisé pour caractériser l'enroulement des deux brins en double hélice de l'ADN. Le théorème (2) est utilisé pour caractériser l'influence des déformations géométriques de l'ADN sur le surenroulement (en).
Lien externe
(en)Eric W. Weisstein, « Călugăreanu Theorem », MathWorld
Portail des mathématiques
这样 (2,4)-环面链环的两条曲线的环绕数是 4。
在数学中,环绕数(linking number)是描述三维空间中两条闭曲线环绕的一个数值不变量。直观上,环绕数表示每一条曲线缠绕另一条曲线的次数。环绕数总是整数,但有可能取正数或负数,取决于这两条曲线的定向。
环绕数由高斯以环绕积分的形式引入。它在纽结理论、代数拓扑和微分几何的研究中是重要的对象,并在数学和科学中有许多应用,包括量子力学、电磁学以及 DNA超螺旋的研究。
定义
空间中任何两条闭曲线都恰好可以移动成如下标准位置之一。这决定了环绕数: 环绕数 -2 环绕数 -1 环绕数 0 环绕数 1 环绕数 2 环绕数 3 每条曲线在移动过程中可以穿过自身,但这两条曲线保持互相分离。
计算环绕数
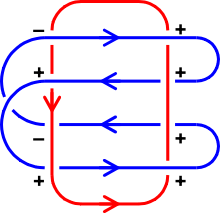
存在一个算法计算出一个链环图表的环绕数。按如下法则将每个交叉标记为“正”或“负” :

正交叉数总数减去负交叉数总数等于环绕数的两倍,即
-
环绕数
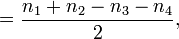
这里 n1, n2, n3, n4 分别表示四类交叉数的个数。两个和 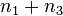 与
与  总相等。这样得到了如下另外的公式
总相等。这样得到了如下另外的公式
-
环绕数
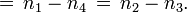
注意到  只涉及到蓝曲线被红曲线下交叉,而
只涉及到蓝曲线被红曲线下交叉,而  只涉及到上交叉。
只涉及到上交叉。
性质与例子
任何两条没有链接起来的曲线相交数为零。但环绕数为零的两条曲线仍可能是链接起来的(例如右图的怀特黑德链环(Whitehead link))。
逆转任何一条曲线的定向,环绕数改变符号;但两条曲线同时逆转定向,环绕数不变。
环绕数具有手征性:取一个链环的镜像,环绕数改变符号。我们对正环绕数的约定基于右手法则。
x-y 平面上一条定向曲线的卷绕数等于它与 z-轴(将 z-轴想象为三维球面中一条闭曲线)的环绕数。
更一般地,如果其中一条曲线是简单的,则这个分支的第一同调群同构于整数 Z。在此情形,环绕数由另一条曲线的同调类决定。
在物理学中,环绕数是拓扑量子数之一例,它与量子纠缠有关。
高斯的积分定义
给定两条不交可微曲线 ,定义从环面到单位球面高斯映射 为 取单位球面上一点 v,从而链环的正交投影到垂直于 v 的平面给出一个链环图表。观察到点 (s, t) 在高斯映射下映为 v 对应于链环图表中一个交叉,这里 在 上。并且 (s, t) 的一个邻域在高斯映射下映为 v 的一个邻域,保持或逆转定向取决于交叉的符号。从而为了计算这个对应于 v 的链环图表的环绕数,只需数高斯映射复盖 v 的带符号次数。由于 v 是一个正则值,这恰是高斯映射的度数(即 Γ 的像盖住球面的带符号次数)。环绕数的同痕不变性自动由度数在同伦下不变得到。任何其它正则值将得到相同的数,所以环绕数与任何特定的链环图表无关。 曲线 γ1 与 γ2 的环绕数的这种表述给出了用二重线积分表示的一个明确公式,即高斯环绕积分: 环绕数 这个积分求出了高斯映射像的全部带符号面积(被积函数是 Γ 的雅可比矩阵),然后除以球面的面积(等于 4π)。
推广
就像三维中环绕的闭曲线,任何两个维数为 m 与 n 的闭流形,可能在 维欧几里得空间中环绕起来。任何这样链环有一个相伴的高斯映射,其度数是环绕数的推广。
任何标架纽结(framed knot)有一个自环绕数,得自计算纽结 C 与将曲线 C 中的点沿着标架矢量稍微移动得到一条新曲线的环绕数。由铅直移动(沿着黑板标架)得到的自环绕数称为考夫曼自环绕数(Kauffman's self-linking number)。
另见
卷绕数
曲线的微分几何
链环(Link)
霍普夫不变量(Hopf invariant)
吻接数(kissing number)
翻滚数(writhe)

 词典释义:
词典释义:
 交错
交错


 搂搂抱抱
搂搂抱抱 ;
; 欲;
欲;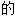 ,色
,色
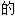 ,淫荡
,淫荡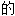 ,好色
,好色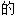 ;
; ;
;