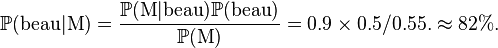Le terme probabilité possède plusieurs sens : venu historiquement du latin probabilitas, il désigne l'opposé du concept de certitude ; il est également une évaluation du caractère probable d'un événement, c'est-à-dire qu'une valeur permet de représenter son degré de certitude ; récemment, la probabilité est devenue une science mathématique et est appelée théorie des probabilités ou plus simplement probabilités; enfin une doctrine porte également le nom de probabilisme.
La probabilité d'un événement est un nombre réel compris entre 0 et 1. Plus ce nombre est grand, plus le risque, ou la chance, que l'événement se produise est grand. L'étude scientifique des probabilités est relativement récente dans l'histoire des mathématiques. L'étude des probabilités a connu de nombreux développements depuis le XVIII siècle grâce à l'étude de l'aspect aléatoire et en partie imprévisible de certains phénomènes, en particulier les jeux de hasard. Ceux-ci ont conduit les mathématiciens à développer une théorie qui a ensuite eu des implications dans des domaines aussi variés que la météorologie, la finance ou la chimie.
Historique
À l'origine, dans les traductions d'Aristote, le mot « probabilité » ne désigne pas une quantification du caractère aléatoire d'un fait mais l'idée qu'une idée est communément admise par tous. Ce n'est qu'au cours du Moyen Âge puis de la Renaissance autour des commentaires successifs et des imprécisions de traduction de l'œuvre d'Aristote que ce terme connaîtra un glissement sémantique pour finir par désigner la vraisemblance d'une idée.
L'apparition de la notion de « risque », préalable à l'étude des probabilités, n'est apparue qu'au XII siècle pour l'évaluation de contrats commerciaux avec le Traité des contrats de Pierre de Jean Olivi, et s'est développée au XVI siècle avec la généralisation des contrats d'assurance maritime. À part quelques considérations élémentaires par Girolamo Cardano au début du XVI siècle et par Galilée au début du XVII siècle, le véritable début de la théorie des probabilités date de la correspondance entre Pierre de Fermat et Blaise Pascal en 1654.
C'est dans la deuxième moitié du XVII siècle, à la suite des travaux de Blaise Pascal, Pierre de Fermat et Christian Huygens sur le problème des partis que le terme « probabilité » prend peu à peu son sens actuel avec les développements du traitement mathématique du sujet par Jakob Bernoulli.
Au XVIII siècle, Gabriel Cramer donne un cours sur la logique probabiliste qui deviendra une base à l'article probabilité de l'encyclopédie de Diderot écrite à la fin de ce même siècle. Ce n'est alors qu'au XIX siècle qu'apparaît ce qui peut être considéré comme la théorie moderne des probabilités en mathématiques.
Le calcul des probabilités prend un nouvel essor au début du XX siècle avec l'axiomatique de Kolmogorov, commence alors la théorie des probabilités. Les probabilités deviennent une science et une théorie comme branche des mathématiques.
Terminologies
Ainsi il existe plusieurs notions que nous détaillerons dans les sections suivantes :
la probabilité d'un fait caractérise la possibilité que ce fait se produise, une vraisemblance, une apparence de vérité. (définition 2 du Larousse). Le probable, la connaissance probable ou la logique probabiliste sont des termes utilisés notamment au XVIII siècle pour désigner une connaissance intermédiaire entre la certitude de la vérité et la certitude de la fausseté. Voir l'article du wiktionnaire : probable,
les probabilités d'un fait donnent le pourcentage de chance qu'un fait se produise, c'est-à-dire qu'elles donnent une ou plusieurs valeurs (ou pourcentage) de la possibilité qu'il se produise. Cette notion se rapproche de la notion mathématique de loi de probabilité (définition 1 du Larousse). Plus formellement c'est le rapport du nombre de cas favorables au nombre de cas possibles. Voir l'article : probabilités (mathématiques élémentaires),
les probabilités ou le calcul des probabilités ou la théorie des probabilités est la théorie mathématique qui étudie le caractère probable des événements (définition 1 du Larousse). Voir l'article : théorie des probabilités,
la doctrine des probabilité ou probabilisme est une doctrine de théologie morale qui enseigne qu'on peut suivre une opinion pourvu qu'elle soit probable. Voir l'article : probabilisme.
Probabilité et certitude
Le premier usage du mot probabilité apparaît en 1370 avec la traduction de l'éthique à Nicomaque d'Aristote par Oresme et désigne alors « le caractère de ce qui est probable ». Le concept de probable chez Aristote (ενδοξον, en grec) est ainsi défini dans les Topiques :
« Sont probables les opinions qui sont reçues par tous les hommes, ou par la plupart d’entre eux, ou par les sages, et parmi ces derniers, soit par tous, soit par la plupart, soit enfin par les plus notables et les plus illustres »
Ce qui rend une opinion probable chez Aristote est son caractère généralement admis; ce n'est qu'avec la traduction de Cicéron des Topiques d'Aristote, qui traduit par probabilis ou par verisimilis, que la notion de vraisemblance est associée à celle de « probabilité » ce qui aura un impact au cours du Moyen Âge puis de la Renaissance avec les commentaires successifs de l'œuvre d'Aristote.
Une phrase, situation ou proposition est vraie ou fausse. Sa probabilité est la « connaissance évidente de la vérité ou de la fausseté d'une proposition ». La notion d'incertitude est quant à elle le défaut de cette connaissance. Pour une proposition, il existe alors trois cas :
La proposition est reconnue comme vraie avec certitude,
La proposition est reconnue comme fausse avec certitude,
Elle est probable si on ne peut la reconnaître vraie ou fausse. Dans ce cas, il est possible de mesurer une certaine vraisemblance par la connaissance du nombre de conditions requises pour être reconnue vraie.
Cette représentation développée par Cramer permet de faire apparaître une manière de mesurer la notion d'incertitude ou de probable. Il donne alors la définition suivante de la probabilité :
Définition (Gabriel Cramer) — Puisque la certitude entière naît de l'assurance que l'on a de l'existence de toutes les conditions requises pour certaines vérités, et la probabilité de la connaissance qu'on a de l'existence de quelques-unes de ces conditions, on regarde la certitude comme un tout et la probabilité comme une partie. Le juste degré de probabilité d'une proposition sera donc exactement connu quand on pourra dire et prouver que cette probabilité monte à demi certitude ou au trois quarts de la certitude entière, ou seulement au tiers de la certitude, etc.
Les probabilités d'un événement
Comme précisé précédemment, la notion de probabilité permet de quantifier le hasard. La formalisation du début du XX siècle est aujourd'hui unanimement utilisée. (par exemple, voir l'ouvrage de Jacod et Protter pour cette section)
La probabilité d'un certain événement A, notée , associe une valeur entre 0 et 1 que l'événement se réalise. Lorsque , l'événement est dit presque sûr (ou quasi certain), c'est-à-dire qu'il a « toutes les chances » de se réaliser. À l'inverse si , A est dit négligeable (ou quasi impossible), c'est-à-dire qu'il a une chance nulle de se réaliser.
La probabilité d'un événement A peut s'obtenir de manière fréquentiste, notamment lorsqu'il est possible de faire une expérience plusieurs fois et de compter le nombre de succès de l'expérience. En effet, si on effectue n fois une expérience et que dans 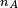 fois des cas, l'événement A est réalisé, alors, la probabilité de A est donnée par :
fois des cas, l'événement A est réalisé, alors, la probabilité de A est donnée par :
-
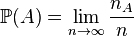 .
.
De manière plus probabiliste, lorsque le nombre de résultats possible de l'expérience est fini, la probabilité de A est définie par :
-
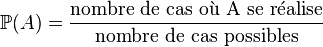 .
.
Mathématiquement, l'événement A est un sous-ensemble d'un ensemble qui représente toutes les éventualités possibles. Pour obtenir une théorie, des axiomes ont été proposés par Kolmogorov : la probabilité doit vérifier :
pour tout événement , ,
,
pour .
Grâce à cette description, plusieurs notions peuvent s'écrire de manière mathématique.
Deux événements sont dits indépendants si le fait de connaître la probabilité du premier événement ne nous aide pas pour prévoir la probabilité du second et inversement. Mathématiquement, cela s'écrit : 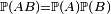 . Par exemple, la probabilité d'obtenir un as à un premier jeté de dé et d'obtenir un as au deuxième jeté de dé est la multiplication des deux probabilités et vaut 1/36.
. Par exemple, la probabilité d'obtenir un as à un premier jeté de dé et d'obtenir un as au deuxième jeté de dé est la multiplication des deux probabilités et vaut 1/36.
Il est possible de considérer la probabilité d'un événement (notons le A) conditionnellement à un autre (noté B). Lorsque les deux événements ne sont pas indépendants, le fait de connaître la probabilité de l'un influence la probabilité de l'autre par la formule : 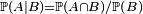 . Par exemple, la probabilité d'obtenir la somme des deux dés égale à 12 lorsque le premier dé a donné 6 vaut 1/6.
. Par exemple, la probabilité d'obtenir la somme des deux dés égale à 12 lorsque le premier dé a donné 6 vaut 1/6.
Des formules existent pour pouvoir calculer tout type de probabilité. C'est le cas de la formule de Poincaré, de la formule des probabilités totales ou du théorème de Bayes.
Théorie des probabilités
Encouragé par Pascal, Christian Huygens publie De ratiociniis in ludo aleae (raisonnements sur les jeux de dés) en 1657. Ce livre est le premier ouvrage important sur les probabilités. Il y définit la notion d'espérance et y développe plusieurs problèmes de partages de gains lors de jeux ou de tirages dans des urnes. Deux ouvrages fondateurs sont également à noter : Ars Conjectandi de Jacques Bernoulli (posthume, 1713) qui définit la notion de variable aléatoire et donne la première version de la loi des grands nombres, et Théorie de la probabilité d' Abraham de Moivre (1718) qui généralise l'usage de la combinatoire.
La théorie de la probabilité classique ne prend réellement son essor qu'avec les notions de mesure et d'ensembles mesurables qu'Émile Borel introduit en 1897. Cette notion de mesure est complétée par Henri Léon Lebesgue et sa théorie de l'intégration. La première version moderne du théorème central limite est donné par Alexandre Liapounov en 1901 et la première preuve du théorème moderne est donnée par Paul Lévy en 1910. En 1902, Andrei Markov introduit les chaînes de Markov pour entreprendre une généralisation de la loi des grands nombres pour une suite d'expériences dépendant les unes des autres. Ces chaînes de Markov connaîtront de nombreuses applications entre autres pour modéliser la diffusion ou pour l'indexation de sites internet sur Google.
Il faudra attendre 1933 pour que la théorie des probabilités sorte d'un ensemble de méthodes et d'exemples divers et devienne une véritable théorie, axiomatisée par Kolmogorov.
Kiyoshi Itô met en place une théorie et un lemme qui porte son nom dans les années 1940. Ceux-ci permettent de relier le calcul stochastique et les équations aux dérivées partielles faisant ainsi le lien entre analyse et probabilités. Le mathématicien Wolfgang Doeblin avait de son côté ébauché une théorie similaire avant de se suicider à la défaite de son bataillon en juin 1940. Ses travaux furent envoyés à l'Académie des sciences dans un pli cacheté qui ne fut ouvert qu'en 2000.
Axiomatique
Au début du XX siècle, Kolmogorov définit des axiomes mathématiques afin de pouvoir étudier le hasard. Ainsi il construit l'espace des possibles appelé univers qui contient tous les hasards possibles, il le munit d'un ensemble qui contient les sous-ensembles de l'univers appelé tribu et d'une mesure de probabilité qui permet de calculer les probabilités correspondantes. L'espace ainsi construit vérifie les trois axiomes des probabilités :
(positivité) la probabilité d'un événement est une valeur entre 0 et 1 : pour tout , ,
(masse unitaire) la probabilité de l'univers est 1 : ,
(additivité) pour toute suite dénombrable d'événements disjoints deux à deux, c'est-à-dire tels que pour tous , alors .
Variables aléatoires, lois et caractérisations
Afin de pouvoir mieux manipuler le hasard, il est commode d'utiliser une variable aléatoire. Elle peut être réelle, mais peut aussi être un multidimensionnelle ou même plus générale. Cette variable réelle est, en théorie, une application : qui à chaque aléa , associe le résultat de l'expérience : .
Cette variable possède une répartition de ces valeurs donnée par sa loi de probabilité qui est une mesure. Cette dernière peut être représentée de nombreuses manières, les plus communes sont par l'utilisation de la fonction de répartition, la densité de probabilité (si elle existe) ou la fonction de masse le cas échéant. De nombreuses propriétés des lois de probabilité, et donc des variables aléatoires, peuvent être étudiées : espérance, moments, indépendance entre plusieurs variables, etc.
Convergence et théorèmes limites
Il est possible de considérer une infinité de variables aléatoires : . Dans ce cas, y a-t-il une limite possible? La question de notion de convergence aléatoire se pose alors. Il existe plusieurs types de convergences : la convergence en loi qui est la convergence de la loi de la variable (en tant que mesure), la convergence en probabilité, la convergence presque sûre ou encore la convergence en moyenne.
De nombreux théorèmes limites existent alors. Les plus connus sont : la loi des grands nombres qui annonce que la moyenne des n premières variables aléatoires converge vers la moyenne théorique de la loi commune des variables aléatoires ; le théorème central limite qui donne la bonne renormalisation de la somme des variables aléatoires pour avoir une limite non triviale.
Calcul stochastique
Le calcul stochastique est l'étude des phénomènes qui évoluent au cours du temps de manière aléatoire. Le temps peut être modélisé de manière discrète, c'est-à-dire par les valeurs entières : , dans ce cas le phénomène est représenté par une suite (infinie) de variables aléatoires : , c'est une marche aléatoire. Le temps peut également être modélisé de manière continue c'est-à-dire par des valeurs réelles ou , il s'agit alors d'un processus stochastique .
Plusieurs propriétés sont alors liées au calcul stochastique : la propriété de Markov annonce que le mouvement futur du phénomène ne dépend que de l'état présent et non pas du mouvement passé ; la récurrence et la transience d'une chaîne de Markov assurent le retour ou le passage unique en un état donné ; une martingale est un processus tel que l'état futur est déterminé en moyenne par l'état présent, etc.
Doctrine des probabilités
La doctrine de la probabilité, autrement appelée probabilisme, est une théologie morale catholique qui s'est développée au cours du XVI siècle sous l'influence entre autres de Bartolomé de Medina et des jésuites. Avec l'apparition de la doctrine de la probabilité, ce terme connaîtra un glissement sémantique pour finir par désigner au milieu du XVII siècle le caractère vraisemblable d'une idée.
La probabilité d'une opinion désigne alors au milieu du XVII siècle la probabilité qu'une opinion soit vraie. Ce n'est qu'à partir de la fin du XVII siècle avec l'émergence de la probabilité mathématique que la notion de probabilité ne concernera plus seulement les opinions et les idées mais aussi les faits et se rapprochera de la notion de hasard que l'on connaît aujourd'hui.
Interprétation des probabilités
Lors de l'étude d'un phénomène aléatoire, il existe plusieurs façons d'aborder la notion de probabilité liée à ce phénomène.
La conception subjective de la probabilité d'un événement s'applique dans le cas où il est difficile, voire impossible, de connaître les différentes probabilités des résultats d'une expérience aléatoire. Notamment dans le cas où l'expérience ne peut se réaliser plusieurs fois dans les mêmes conditions. Les probabilités attribuées ne correspondent alors pas exactement à la réalité et leurs estimations peuvent varier selon les personnes et les situations. On parle dans ce cas de probabilité épistémique ou de probabilité bayésienne. Il s'agit d'une probabilité s'appliquant au jugement que l'on porte plus que sur l'événement lui-même. Par exemple : quelle est la probabilité de réussir à un examen? Pour connaître les chances d'obtenir une note donnée à un examen, il faut l'estimer suivant le candidat et sa situation par rapport à l'examen. Il n'est pas possible de réaliser plusieurs fois l'expérience puisqu'un examen ne peut se passer plus d'une fois dans la même configuration. Les probabilités estimées et choisies pour chaque note vérifient les axiomes de Kolmogorov mais sont subjectives.
La conception fréquentiste des probabilité d'un événement est plus historique. Elle permet d'attribuer les chances de réalisation de chaque événement par une méthode statistique, c'est-à-dire en réalisant plusieurs fois l'expérience et d'en déduire les probabilités liées aux événements. Idéalement il faudrait répéter l'expérience à l'infini pour obtenir les probabilités réelles de l'expérience, cependant, puisque ce n'est pas possible, les méthodes expérimentales donnent des probabilités empiriques. (voir la section Les probabilités d'un événement ci-dessus). Cette notion s'appelle également probabilité statistique ou probabilité a posteriori. Par exemple : un joueur possède un dé pipé dont il ne connaît pas le biais, c'est-à-dire que les valeurs du dé n'ont pas les mêmes chances d'apparaître. Une méthode possible est de réaliser un grand nombre de lancers et de compter les résultats obtenus. Les résultats sont alors approchés pour vérifier l'axiomatique de Kolmogorov.
La conception classique de la probabilité s'utilise dans le cas de situations prédéfinies considérées comme connues. Beaucoup de situations sont considérées comme aléatoires et équiprobables, c'est-à-dire que chaque événement élémentaire à la même chance d'apparaître. Cette conception est également appelée objective, probabilité mathématique ou probabilité a priori Par exemple : un dé (non pipé) est supposé équilibré, c'est-à-dire que chaque valeur a une chance sur six d'apparaître. Lors d'une distribution de cartes, chaque donne est supposée apparaître avec les mêmes chances
Une notion philosophique apparaît alors : puisque nous ne connaissons la nature et le monde autour de nous que par notre expérience et notre point de vue, nous ne le connaissons que de manière subjective et ne pouvons estimer précisément les lois objectives qui les dirigent.
Applications
Les jeux de hasard sont l'application la plus naturelle des probabilités mais de nombreux autres domaines s'appuient ou se servent des probabilités. Citons entre autres :
la statistique est un vaste domaine qui s'appuie sur les probabilités pour le traitement et l'interprétation des données.
La théorie des jeux s'appuie fortement sur la probabilité et est utile en économie et plus précisément en micro-économie.
l'estimation optimale par usage de la loi de Bayes, qui sert de fondement à une grande partie des applications de décision automatique (imagerie médicale, astronomie, reconnaissance de caractères, filtres anti-pourriel).
En physique ainsi qu'en biologie moléculaire l'étude du mouvement brownien pour de petites particules ainsi que les équations de Fokker-Planck font intervenir des concepts s'appuyant sur le calcul stochastique et la marche aléatoire
les mathématiques financières font un large usage de la théorie des probabilités pour l'étude des cours de la bourse et des produits dérivés. Citons par exemple le Modèle de Black-Scholes pour déterminer le prix de certains actifs financiers (notamment les options).
les études probabilistes de sûreté où l'on évalue la probabilité d'occurrence d'un événement indésirable. C'est devenu un outil d'évaluation des risques dans bon nombre d'installations industrielles.
Liens avec la statistique
Il existe plusieurs façons d'aborder les probabilités : le calcul a priori et le calcul a posteriori. (voir la section interprétation des probabilités ci-dessus). Le calcul des probabilités a posteriori correspond à une attribution des valeurs des probabilités inconnues par une manière statistique.
Pour estimer les probabilités, les estimateurs statistiques sont utilisés afin de mieux approcher la variable recherchée. Un estimateur est une valeur calculée à partir d'un échantillon de la population totale étudiée. Un estimateur est bien choisi, c'est-à-dire qu'il donnera une bonne estimation des valeurs recherchées, si c'est un estimateur sans biais et convergent ; autrement dit la moyenne empirique approche la moyenne théorique et l'estimateur converge vers la bonne variable aléatoire lorsque la taille de l'échantillon augmente. La méthode du maximum de vraisemblance permet de choisir un bon estimateur.
Par ces méthodes, il est possible de retrouver les paramètres inconnus d'une loi de probabilité associée au phénomène étudié.
La révision bayésienne est une autre méthode pour le calcul des probabilités a priori. Celle-ci se fait grâce au théorème de Bayes :
-
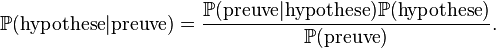
Dans cette formule, l'hypothèse représente ce que l'on suppose a priori sur le phénomène aléatoire, la preuve est une partie du phénomène que l'on connaît et que l'on peut mesurer. Ainsi 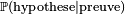 permet de mesurer la vraisemblance de l'hypothèse que l'on fixe.
permet de mesurer la vraisemblance de l'hypothèse que l'on fixe.
-
Exemple 1
La fréquence empirique permet d'estimer les probabilités. Dans un échantillon de n individus, il suffit de compter le nombre de fois où l'individu appartient à la catégorie A recherchée. En notant ce nombre parmi les n tirages, la fréquence est proche de la probabilité recherchée. Lors de 400 lancers de pièces, si il apparaît 198 fois le côté face, alors on en déduit que la probabilité d'obtenir face est . C'est un cas particulier de la loi des grands nombres.
-
Exemple 2
Une liste de valeurs est connue, elle est supposée de loi normale dont la moyenne m est connue. La question est de trouver l'écart type de la loi normale. La statistique T définie par est un estimateur de , c'est-à-dire qu'il tend vers lorsque n tend vers l'infini.
-
Exemple 3
On se demande quel temps il fera demain, la météo permet d'obtenir des informations supplémentaires. Certaines données sont alors connues : la probabilité que la météo annonce un beau temps sachant qu'il fera effectivement beau : 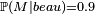 , la probabilité que la météo annonce un beau temps sachant qu'il pleuvra :
, la probabilité que la météo annonce un beau temps sachant qu'il pleuvra : 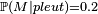 .
.
Une hypothèse est choisie : par exemple 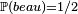 , c'est-à-dire que l'on considère, a priori, qu'il y a une chance sur deux qu'il fera beau demain.
, c'est-à-dire que l'on considère, a priori, qu'il y a une chance sur deux qu'il fera beau demain.
Il est alors possible de calculer la probabilité que la météo annonce un beau temps :  , c'est-à-dire que la météo annonce un beau temps dans 55 % des cas. La probabilité qu'il fera beau demain sachant que la météo a annoncé beau temps est alors donnée par :
, c'est-à-dire que la météo annonce un beau temps dans 55 % des cas. La probabilité qu'il fera beau demain sachant que la météo a annoncé beau temps est alors donnée par :
-
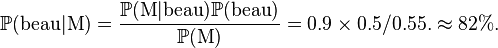
Il est alors possible de réviser une deuxième fois l'hypothèse qu'il fera beau en regardant un deuxième bulletin météo d'une source différente. On prendrait alors comme nouvelle hypothèse la probabilité d'avoir un beau temps nouvellement calculée.

 词典释义:
词典释义:
 能
能
 失败不是一定
失败不是一定 但完全是有
但完全是有 能
能 。
。 能…, 恐怕…
能…, 恐怕… 能, 大概, 或然
能, 大概, 或然 能
能 能到
能到 ……
……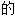 ,能……
,能……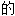
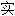
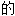 ;
; 接纳
接纳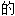 ,很像真
,很像真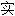
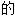 ;
; 能
能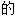 ;
; ,假设
,假设 ,推测
,推测 ;
; 能,大概,或许;
能,大概,或许; 能;
能; 能
能 ,
, 能存在
能存在 ,
, 能发生
能发生 ;
; ;
; ,不
,不 避免
避免 ,必然
,必然 ;
;
 ,
, 而易见
而易见 ,一目了然
,一目了然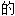 ,
,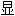 著
著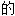 ;
; 能
能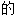 , 或然
, 或然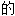 ; 概率性
; 概率性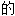 ; 嫌疑犯
; 嫌疑犯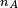 fois des cas, l'événement
fois des cas, l'événement 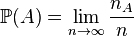 .
.
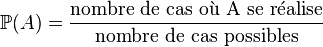 .
.
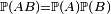 . Par exemple, la probabilité d'obtenir un as à un premier jeté de dé et d'obtenir un as au deuxième jeté de dé est la multiplication des deux probabilités et vaut 1/36.
. Par exemple, la probabilité d'obtenir un as à un premier jeté de dé et d'obtenir un as au deuxième jeté de dé est la multiplication des deux probabilités et vaut 1/36.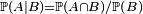 . Par exemple, la probabilité d'obtenir la somme des deux dés égale à 12 lorsque le premier dé a donné 6 vaut 1/6.
. Par exemple, la probabilité d'obtenir la somme des deux dés égale à 12 lorsque le premier dé a donné 6 vaut 1/6.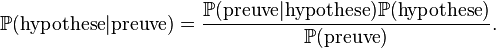
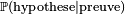 permet de mesurer la vraisemblance de l'hypothèse que l'on fixe.
permet de mesurer la vraisemblance de l'hypothèse que l'on fixe.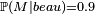 , la probabilité que la météo annonce un beau temps sachant qu'il pleuvra
, la probabilité que la météo annonce un beau temps sachant qu'il pleuvra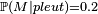 .
.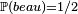 , c'est-à-dire que l'on considère, a priori, qu'il y a une chance sur deux qu'il fera beau demain.
, c'est-à-dire que l'on considère, a priori, qu'il y a une chance sur deux qu'il fera beau demain. , c'est-à-dire que la météo annonce un beau temps dans 55 % des cas. La probabilité qu'il fera beau demain sachant que la météo a annoncé beau temps est alors donnée par
, c'est-à-dire que la météo annonce un beau temps dans 55 % des cas. La probabilité qu'il fera beau demain sachant que la météo a annoncé beau temps est alors donnée par