Derrière le terme de congruence se cachent des notions semblables mais de niveaux d'abstraction différents. Historiquement, la notion de congruence sur les entiers relatifs a été introduite par Gauss vers 1801.
Sciences exactes
En arithmétique modulaire, deux entiers relatifs sont congrus modulo n s'ils ont le même reste dans la division euclidienne par n. Exemple : 7 et 10 sont congrus modulo 3, puisque leurs division par 3 donne le même reste 1. On peut donc aussi dire qu'ils sont congrus modulo n si leur différence est un multiple de n.
Dans la mesure des angles orientés, on dit que deux mesures sont congrues modulo 2π si et seulement si leur différence est un multiple de 2π. Cela caractérise deux mesures d'un même angle.
En algèbre, on parle de congruence modulo I dans un anneau commutatif (R, +, *) dont I est un idéal : x est congru à y modulo I si et seulement si x - y appartient à I. Cette congruence est une relation d'équivalence, compatible avec les opérations + et * et permet de définir un anneau quotient R/I. Les deux notions précédentes deviennent alors des cas particuliers de cette définition plus générale. de congruence modulo H dans un groupe G quand H est un sous-groupe de G. x est congru à y modulo H si et seulement si appartient à H. Cette relation est une relation d'équivalence permettant de construire un ensemble quotient qui, si H est un sous-groupe distingué, est un groupe quotient. de congruence dans un semi-groupe (G,*) pour toute relation d'équivalence compatible avec la loi *. Cette définition est alors plus large que la précédente mais on ne parle alors plus de congruence modulo ...
de congruence modulo I dans un anneau commutatif (R, +, *) dont I est un idéal : x est congru à y modulo I si et seulement si x - y appartient à I. Cette congruence est une relation d'équivalence, compatible avec les opérations + et * et permet de définir un anneau quotient R/I. Les deux notions précédentes deviennent alors des cas particuliers de cette définition plus générale.
de congruence modulo H dans un groupe G quand H est un sous-groupe de G. x est congru à y modulo H si et seulement si appartient à H. Cette relation est une relation d'équivalence permettant de construire un ensemble quotient qui, si H est un sous-groupe distingué, est un groupe quotient.
de congruence dans un semi-groupe (G,*) pour toute relation d'équivalence compatible avec la loi *. Cette définition est alors plus large que la précédente mais on ne parle alors plus de congruence modulo ...
Toujours en algèbre, deux matrices carrées sont dites congruentes si elles représentent la même forme bilinéaire dans deux bases différentes.
En géométrie riemannienne, une congruence est l'ensemble des courbes intégrales associées à un champ de vecteurs.
On trouve parfois, sous l'influence de l'anglais, le terme de congruent mis à la place de isométrique. Il s'agit alors d'une simple relation d'équivalence sur l'ensemble des figures planes.
En anatomie, on parle de congruence des surfaces articulaires. Deux surfaces sont congruentes lorsqu'il y a un emboitement parfait, c'est le cas de l'articulation coxo-fémorale. Contrairement à l'articulation du genou où les surfaces articulaires sont rendues congruentes par les ménisques.
En phylogénie, on parle de congruence entre deux arbres lorsqu'ils sont symétriques et montrent une coévolution entre deux groupes (exemple hôtes/parasites).
Sciences humaines et sociales
En psychothérapie, congruence est le terme employé par Carl Rogers pour indiquer une correspondance exacte entre l'expérience et la prise de conscience.
En géographie, la congruence est « l'adaptation réciproque ».
En sémiotique, on parle de congruence lorsque des homologies partielles peuvent être établies entre différentes couches de signification, au sein d'un système pluri-isotopique. On parle, en littérature, de congruence entre isotopies ou entre schémas narratifs, ou encore de congruence énonciative.

 词典释义:
词典释义:

 , 合适
, 合适 , 和谐
, 和谐
 , 全等
, 全等 , 相合
, 相合 , 同余
, 同余 :
:
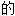 ;
;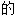 ,结构紧密
,结构紧密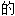 ,严密
,严密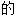 ,一致
,一致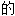 ,协调
,协调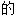 ;
;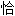
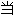
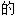 ,贴切
,贴切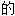 ,确切
,确切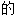 ,
,

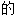 ;
;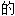 ,积极
,积极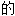 ,有创造性
,有创造性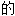 ;
;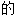 ,反对
,反对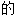 ,对立
,对立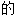 ;
;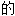 ;
; ,相异
,相异 ;
; ,自发
,自发 ,自动
,自动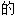 ;
;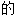 ;
;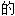 ,清晰
,清晰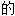 ;
; ,积极
,积极 ;
;