En géométrie, la notion générale d'angle se décline en plusieurs concepts apparentés.
Dans son sens ancien, l'angle est une figure plane, portion de plan délimitée par deux droites sécantes. C'est ainsi qu'on parle des angles d'un polygone. Cependant, l'usage est maintenant d'employer le terme « secteur angulaire » pour une telle figure. L'angle peut désigner également une portion de l'espace délimitée par deux plans (angle dièdre). La mesure de tels angles porte couramment mais abusivement le nom d'angle elle aussi.
En un sens plus abstrait, l'angle est une classe d'équivalence, c'est-à-dire un ensemble obtenu en assimilant entre eux tous les angles-figures identifiables par isométrie. L'une quelconque des figures identifiées est alors appelée représentant de l'angle. Tous ces représentants ayant même mesure, on peut parler de mesure de l'angle abstrait.
Il est possible de définir une notion d'angle orienté en géométrie euclidienne du plan, ainsi que d'étendre la notion d'angle au cadre des espaces vectoriels préhilbertiens ou des variétés riemanniennes.
Histoire
Le mot angle dérive du latin angulus, mot qui signifie « le coin ». Selon le mathématicien Carpos d'Antioche, l'angle est une quantité et l'intervalle des lignes ou des surfaces qui le comprennent ; cet intervalle est dimensionné d'une seule manière, et pourtant l'angle n'est pas une ligne pour cela.
L'angle comme figure du plan ou de l'espace
Secteur angulaire et angle
Un secteur angulaire est une figure plane obtenue par intersection ou réunion de deux demi-plans délimités par des droites sécantes ou confondues.
L'angle d'un secteur angulaire est le nombre réel positif qui mesure la proportion du plan occupée par le secteur angulaire. Les unités utilisées pour le quantifier sont le radian, le quadrant et ses subdivisions le degré, ses sous-unités et le grade. Les angles sont fréquemment notés par une lettre grecque minuscule, par exemple α, β, θ, ρ... Lorsque l'angle est au sommet d'un polygone et qu'il n'y a pas d'ambiguïté, on utilise alors le nom du sommet surmonté d'un chapeau, par exemple Â.
L'angle peut aussi s'interpréter comme l'ouverture du secteur angulaire, c'est-à-dire la « vitesse » à laquelle s'éloignent les droites l'une de l'autre lorsque l'on s'éloigne du point d'intersection. C'est la mesure de l'inclinaison d'une droite par rapport à l'autre.
Valeur d'un angle
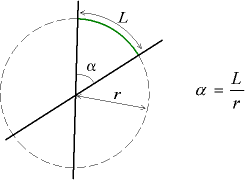
Pour évaluer cet angle, cette « proportion de surface », on prend un disque centré au point d'intersection, et on effectue le rapport entre l'aire de la portion de disque interceptée par le secteur angulaire et l'aire totale du disque. On peut montrer que cela revient également à faire le rapport entre la longueur de l'arc intercepté et la circonférence du cercle ; cette valeur inférieure à 1 est appelée nombre de tour. La valeur 1/4 (quart de tour) correspond au quadrant.
Une unité couramment utilisée est le degré, qui est le résultat de la division du quadrant en 90 parts égales. Le tour complet correspond donc à 360 degrés. La minute d'arc est un sous-multiple du degré, égale à 1/60 de degré. De même, la seconde d'arc est égale à 1/60 de la minute d'arc, soit 1/3600 de degré. On utilise plus rarement le grade, qui correspond à une subdivision centésimale du quadrant.
L'unité internationale de mesure des angles est cependant le radian, défini comme le rapport entre la longueur de l'arc intercepté et le rayon du cercle. Le tour complet correspond donc à radians.
Les angles peuvent être calculés à partir des longueurs des côtés de polygones, notamment de triangles, en utilisant la trigonométrie.
L'unité de mesure des angles utilisée principalement par les militaires est le millième. Il est l'angle sous lequel on voit 1 mètre à 1 kilomètre. 6283 millièmes correspond à 2π radians ou 360 degrés, soit 360 °/arctan(1 m/1 000 m). Autrement-dit, millième = mrad (milliradian).
« Sur le terrain », les angles peuvent être mesurés avec un appareil appelé goniomètre ; il comporte en général une règle courbe graduée en degrés, appelée rapporteur.
Nom des angles
Les angles correspondant à un nombre entier de quadrants portent un nom particulier
Valeur des angles particulier dans les diverses unités
| angle |
nombre de tours |
nombre de quadrants |
radians |
degré |
grade |
| angle plein |
1 tour |
4 quadrants |
2π rad |
360° |
400 gr |
| angle plat |
1/2 tour |
2 quadrants |
π rad |
180° |
200 gr |
| angle droit |
1/4 de tour |
1 quadrant |
π/2 rad |
90° |
100 gr |
| angle nul |
0 tour |
0 quadrant |
0 rad |
0° |
0 gr |
|
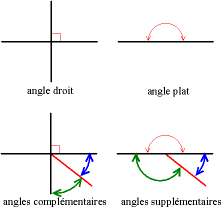
L'angle droit est obtenu en considérant deux droites qui divisent le plan en quatre secteurs égaux. De telles droites sont dites « orthogonales » ou « perpendiculaires ».
Les qualificatifs suivant sont employés pour les angles prenant des valeurs intermédiaires entre ces valeurs remarquables :
l'angle rentrant est un angle supérieur à l'angle plat ;
l'angle saillant est un angle inférieur à l'angle plat ;
l'angle obtus est compris entre 90° et 180° ;
l'angle aigu est compris entre 0° et 90°.
Pour qualifier les valeurs relatives de deux angles, on emploie les expressions suivantes :
deux angles sont complémentaires quand leur somme fait 90 ° ; si deux angles sont complémentaires, chacun est dit être le complément de l'autre ;
deux angles sont supplémentaires quand leur somme fait 180 °.
On emploie encore d'autres expressions pour qualifier la position des angles sur une figure, c'est-à-dire plus justement, la position relative de secteurs angulaires :
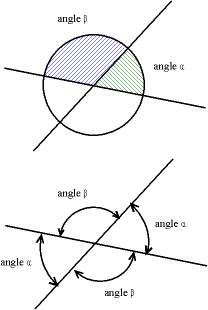
deux secteurs angulaires sont opposés par le sommet, lorsqu'ils ont le même sommet et que les côtés de l'un sont dans le prolongement de ceux de l'autre. Dans ce cas les angles correspondants sont égaux.
deux secteurs angulaires sont adjacents lorsqu'ils ont le même sommet, un côté commun, et que leur intersection est égale à ce côté commun. Les angles s'ajoutent lorsqu'on considère la réunion de ces secteurs.
les angles alternes-externes et les angles alternes-internes sont formés par deux droites coupées par une sécante. Ces angles ont la même mesure lorsque les deux droites sont parallèles.
Remarque, deux angles complémentaires ou supplémentaires ne sont pas nécessairement adjacents : Par exemple, dans un triangle ABE rectangle en B, les angles  et Ê sont complémentaires.
Par extension, on définit également les angles entre des demi-droites, des segments de droite et des vecteurs, en prolongeant les droites portant ces objets jusqu'à leur intersection. La définition par des demi-droites ou des vecteurs permet de lever l'indétermination entre les angles supplémentaires, c'est-à-dire de définir sans ambiguïté quel secteur angulaire utiliser pour définir l'inclinaison des directions.
Angle géométrique
Un angle géométrique est un objet mathématique pouvant être représenté par un secteur angulaire. On peut l'interpréter de plusieurs façons : divergence entre deux directions, directions des faces d'un objet (coin), direction visée par rapport au nord (angle donné par une boussole)…
-
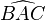 est un angle géométrique.
est un angle géométrique.
On a par ailleurs :
-
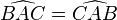
On confond fréquemment « mesure de l'angle » et « angle ». Ainsi par exemple un angle « plat » est appelé abusivement angle « égal » à 180.
Cet abus est appliqué largement dans la suite de cet article.
D'autre part un angle droit par exemple, peut être représenté par plusieurs secteurs angulaires différents, mais comme ils sont tous « superposables », ils représentent tous le même angle. En mathématiques on parle de « classe d'équivalence ».
Angles orientés dans le plan
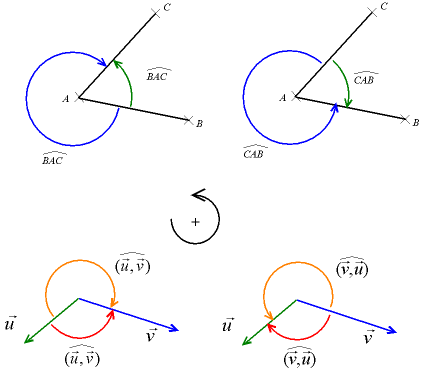
Si le plan est orienté, un même angle peut être déclaré aussi bien positif que négatif, selon le sens dans lequel on « tourne » du premier vecteur au second. Par convention, on oriente le plan dans le sens dit « trigonométrique », c'est-à-dire dans le sens inverse des aiguilles d'une montre (ou « sens anti-horaire »). Si l'on considère deux demi-droites ou vecteurs, alors l'ordre dans lequel on cite les demi-droites ou les vecteurs définit le sens de l'angle, donc son signe ; ainsi :
-
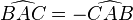
-
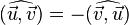
Les angles sont définis à un nombre entier de tours près. Ainsi, le plan complet peut être défini par un tour complet dans le sens positif, deux tours complets dans le sens positif, un tour complet dans le sens négatif... En radians, on dit que les angles sont définis à 2π près (« à-deux-pi-près »). Par exemple, si l'angle α est droit de sens direct, il est noté :
-
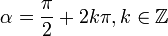
ou bien
-
![\alpha \equiv \frac{\pi}{2} [2\pi]](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/f31f734d59362ebfe8e8378214e8aa7a.png)
Cette dernière notation se lit : « alpha est congru à pi-sur-deux modulo deux-pi ».
On remarque notamment que pour deux demi-droites (ou deux vecteurs) données, le fait de choisir la « petite » ou la « grande » portion de plan importe peu, puisque α ≡ α - 2π (cf. illustration ci-dessus).
Angles orientés de vecteurs
Rotations vectorielles
Rappelons à leur sujet deux points cruciaux pour la suite :
Les isométries positives du plan sont, parmi les transformations préservant les longueurs, celles dont le déterminant vaut 1. Ce sont les rotations vectorielles planes. Elles forment le sous-groupe commutatif SO(2) du groupe orthogonal O(2) du plan.
Proposition.—Si u et v sont deux vecteurs unités distincts, il existe une unique rotation f envoyant u sur v. D'où une application T : (u, v) → f, des couples de vecteurs unitaires vers les rotations.
Un angle orienté de vecteurs est une classe d'équivalence
En disant que (u, v)R(u', v') s'il existe une rotation g telle que u'=g(u) et v'=g(v), on définit une relation d'équivalence R sur les couples de vecteurs unitaires. On appelle angle orienté de vecteurs les classes d'équivalence dans cette relation. En confondant abusivement un représentant et sa classe, on a par exemple : (-u, -v) = (u, v) par le demi-tour.
L'application T : (u, v)→ f « passe au quotient par R » et l'application S obtenue, des classes de R-équivalence vers les rotations, est bijective. Autrement dit :
Théorème — L'angle orienté de vecteurs est caractérisé par la rotation associée : T(u,v) = T(u',v') si et seulement si (u,v)R(u',v').
Démonstration
Par définition, (u,v)R(u',v') si et seulement si la rotation qui envoie u sur u' est la même que celle qui envoie v sur v', autrement dit : T(u,u')=T(v,v'). Par commutativité du groupe des rotations, ceci équivaut à T(u',v)oT(u,u')=T(v,v')oT(u',v), i.e. T(u,v)=T(u',v').
Le choix de l'une des deux orientations du plan détermine l'un des deux isomorphismes du groupe SO(2) des rotations avec le groupe U des nombres complexes de module 1. L'exponentielle complexe permet alors de définir l'angle d'une rotation à 2π près. Si f=T(u, v) est une rotation d'angle , on dira aussi que est une mesure de l'angle orienté de vecteurs (u, v). Pour être digne d'un tel nom, il manque à cette mesure le caractère additif. Avec les angles géométriques, on a des ennuis additifs quand ils sont trop grands ! Pour les angles orientés de vecteurs, il faut d'abord définir la somme...
Les angles orientés de vecteurs forment un groupe
Somme d'angles orientés
La somme est définie en tirant en arrière le long de la bijection S la composition dans SO(2). En confondant un représentant avec sa classe, cela donne :
![(u,v)+(z,t) :=S^{-1} [S(u,v) \circ S(z,t)]](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/e01798711186ccba3ae31816750e9311.png)
Le groupe des angles orientés de vecteurs est commutatif, comme SO(2).
Avec T(u, v)oT(v, w)=T(u, w) on obtient pour les angles la relation de Chasles (u, v)+(v, w)=(u, w)
L'angle plein correspond à l'identité : (u, u) = 0
(v, u)+(u, v) = (v, v) = 0 et donc (v, u) est l'opposé de (u, v)
L'angle plat est la moitié d'un plein : (-Id) o (-Id) = Id. L'angle plat s'écrit donc (u, -u).
Il y a deux angles droits, solutions de 2(u, v) = (u, –u).
Enfin une vraie mesure d'angles
Une orientation du plan étant choisie, la mesure d'un angle orienté de vecteurs est définie par :
 ,
,
où la matrice est celle de T(u, v) dans n'importe quelle base orthonormée directe.
C'est un isomorphisme du groupe des angles orientés dans le groupe additif des « réels modulo 2π » ; ainsi la mesure des angles est enfin additive !
Effet des isométries sur les angles orientés de vecteurs
Les isométries positives conservent les angles orientés de vecteurs par construction.
Les réflexions orthogonales (isométries planes indirectes) renversent les angles orientés de vecteurs : si u et v sont deux vecteurs unitaires non opposés, la réflexion sD d'axe D dirigé par u+v échange u et v et donc (u, v) en son opposé (v, u). Toute réflexion s'obtient en composant sD avec une rotation (on fait tourner l'axe) ; une telle réflexion renverse encore l'angle (u, v).
Angles dans l'espace
Deux droites sécantes sont nécessairement coplanaires, donc l'angle entre les droites est défini dans ce plan, de la même manière que ci-dessus. Pour orienter le plan, on choisit un vecteur normal au plan : le plan est alors orienté dans le sens trigonométrique lorsque le vecteur normal pointe vers l'observateur. Si l'on a défini une base dans ce plan, alors on choisit pour vecteur normal .
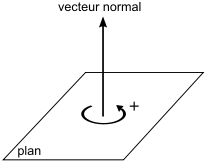
Orientation d'un plan par un vecteur normal
Pour définir l'angle entre deux plans, on considère l'angle que font leurs vecteurs normaux.
Pour définir l'angle entre un plan et une droite, on considère l'angle α entre la droite et sa projection orthogonale sur le plan, ou encore l'angle complémentaire entre la droite et la normale au plan : on retranche l'angle β entre la droite et la normale au plan de l'angle droit (α = π/2 - β en radians).
Pour définir l'angle entre deux droites quelconques de l'espace, on considère l'angle que font leurs vecteurs directeurs (dont le cosinus est égal au produit scalaire de ces vecteurs unitaires), ou encore l'angle planaire que fait une des deux droites avec une quelconque parallèle à l'autre qui la coupe. Cet angle est défini modulo les mêmes choix d'orientation évoqués ci-dessus.
On définit également les angles solides : on prend un point (parfois appelé « point d'observation ») et une surface dans l'espace (la « surface observée »), l'angle solide est la proportion de l'espace délimitée par le cône ayant pour sommet le point considéré et s'appuyant sur le contour de la surface. L'unité est le stéradian (sr en abrégé), l'espace complet fait 4π sr.
Usage
En géodésie (géographie) azimut : angle par rapport à l'axe Nord-Sud sur un plan contenant cet axe et le point visé, compté par rapport au Nord compté dans le sens des aiguilles d'une montre ; latitude : angle que fait une verticale partant d'un point et allant au centre de la Terre par rapport au plan de l'équateur ; les points ayant la même latitude forment un cercle appelé « parallèle » longitude : angle permettant de se repérer sur Terre : angle que fait le plan contenant l'axe Nord-Sud et le point considéré (appelé « plan méridien ») avec un plan de référence contenant aussi l'axe Nord-Sud ; l'intersection d'un plan méridien avec la surface de la Terre est un demi grand-cercle appelé méridien ; le méridien de référence est le méridien de Greenwich droite de hauteur : position d'un point calculé (comprenant azimuth et différence angulaire) par rapport à un point estimé pente : tangente de l'angle d'un terrain vis-à-vis de l'horizontale
azimut : angle par rapport à l'axe Nord-Sud sur un plan contenant cet axe et le point visé, compté par rapport au Nord compté dans le sens des aiguilles d'une montre ;
latitude : angle que fait une verticale partant d'un point et allant au centre de la Terre par rapport au plan de l'équateur ; les points ayant la même latitude forment un cercle appelé « parallèle »
longitude : angle permettant de se repérer sur Terre : angle que fait le plan contenant l'axe Nord-Sud et le point considéré (appelé « plan méridien ») avec un plan de référence contenant aussi l'axe Nord-Sud ; l'intersection d'un plan méridien avec la surface de la Terre est un demi grand-cercle appelé méridien ; le méridien de référence est le méridien de Greenwich
droite de hauteur : position d'un point calculé (comprenant azimuth et différence angulaire) par rapport à un point estimé
pente : tangente de l'angle d'un terrain vis-à-vis de l'horizontale
En astronomie azimut (ou azimuth) : lorsque l'on vise un point depuis le centre de la Terre, angle par rapport à l'axe Nord-Sud sur un plan contenant cet axe et le point visé, compté par rapport au Sud diamètre apparent : angle sous lequel on voit un objet ou un astre distance zénithale : angle entre la verticale et le point visé hauteur : angle entre l'horizontale et le point visé inclinaison : angle entre le plan de l'orbite d'un corps céleste et le plan de référence parallaxe : angle formé par le regard d'une personne qui fixe un point quelconque d'un objet et son changement de position nadir : angle droit vers le bas verticalement par rapport au tour de l'horizon de l'observateur zénith : angle droit vers le haut verticalement par rapport au tour de l'horizon de l'observateur
azimut (ou azimuth) : lorsque l'on vise un point depuis le centre de la Terre, angle par rapport à l'axe Nord-Sud sur un plan contenant cet axe et le point visé, compté par rapport au Sud
diamètre apparent : angle sous lequel on voit un objet ou un astre
distance zénithale : angle entre la verticale et le point visé
hauteur : angle entre l'horizontale et le point visé
inclinaison : angle entre le plan de l'orbite d'un corps céleste et le plan de référence
parallaxe : angle formé par le regard d'une personne qui fixe un point quelconque d'un objet et son changement de position
nadir : angle droit vers le bas verticalement par rapport au tour de l'horizon de l'observateur
zénith : angle droit vers le haut verticalement par rapport au tour de l'horizon de l'observateur
Par ailleurs, la notion d'angle permet de définir une unité de longueur, le parsec
En optique géométrique angle d'incidence : angle entre un vecteur et le vecteur de la surface, par exemple en réflexion et en réfraction, angle entre un rayon lumineux et la normale à la surface d'un dioptre parallaxe
angle d'incidence : angle entre un vecteur et le vecteur de la surface, par exemple en réflexion et en réfraction, angle entre un rayon lumineux et la normale à la surface d'un dioptre
parallaxe
En aérodynamique : angle d'attaque assiette
angle d'attaque
assiette
En balistique hausse
hausse
Angle mort

 词典释义:
词典释义:
 ;
;
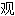 ,
,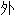 表,
表,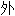 貌;
貌;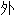 角
角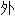 错角
错角 角
角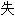 配角
配角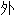 倾角
倾角 角
角 角
角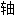
 )
) 调角
调角 角
角 倾角(车轮)
倾角(车轮) 前角
前角
 前角
前角 (轮胎)偏离角
(轮胎)偏离角 节倾角
节倾角 角, 航
角, 航 角
角 角
角 量角
量角 交角
交角 眦
眦
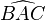 est un angle géométrique.
est un angle géométrique.
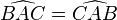
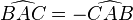
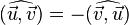
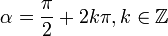
![\alpha \equiv \frac{\pi}{2} [2\pi]](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/f31f734d59362ebfe8e8378214e8aa7a.png)
![(u,v)+(z,t) :=S^{-1} [S(u,v) \circ S(z,t)]](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/e01798711186ccba3ae31816750e9311.png)
 ,
,
