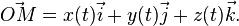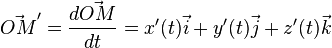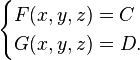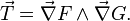En géométrie, le mot courbe, ou ligne courbe désigne certains sous-ensembles du plan, de l'espace usuel. Par exemple, les droites, les segments, les lignes polygonales et les cercles sont des courbes.
La notion générale de courbe se décline en plusieurs objets mathématiques ayant des définitions assez proches : arcs paramétrés, lignes de niveau, sous-variétés de dimension 1. Schématiquement, ces différents modes d'introduction donnent des éclairages complémentaires sur la notion générale de courbe :
Une courbe peut être décrite par un point qui se meut suivant une loi déterminée. La donnée d'une valeur du paramètre temps permet alors de repérer un point sur la courbe. Intuitivement, cela signifie que les courbes sont des objets de dimension 1 ; Une courbe peut être vue comme un domaine du plan ou de l'espace qui vérifie un nombre suffisant de conditions, lui conférant encore un caractère unidimensionnel.
Ainsi une courbe plane peut être représentée dans un repère cartésien par la donnée de lois décrivant abscisse et ordonnée en fonction du paramètre (équation paramétrique)
-

ou encore par la donnée d'une équation cartésienne, ou implicite : 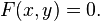
Première approche des invariants associés aux courbes
La géométrie différentielle a pour objectif d'associer aux courbes des objets mathématiques permettant de décrire le mouvement. Les plus intéressants sont ceux qui sont attachés à la courbe, indépendamment de la façon dont elle est parcourue : on définit notamment la longueur d'un arc de courbe, et les concepts de tangente à la courbe, de courbure.
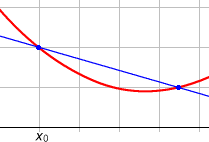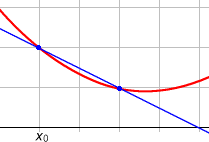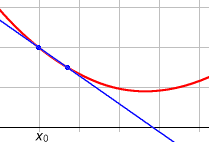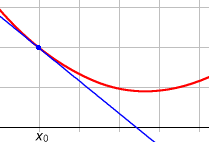
La tangente est limite des sécantes.
Tangente à la courbe
On commence par définir la droite sécante entre deux points M et N de la courbe : c'est la droite qui les relie. La tangente en M peut alors être définie comme la position limite de la sécante lorsque le point N tend vers M.
La tangente en M est également la droite « la plus proche possible » de la courbe au voisinage de M. C'est ce qui explique la proximité entre la notion géométrique de tangente à une courbe, et de dérivée d'une fonction, ou encore de développement limité à l'ordre 1 d'une fonction.
La courbe reste très souvent d'un seul côté de sa tangente, au moins au voisinage du point M. Cependant, en certains points particuliers, appelés points d'inflexion elle traverse sa tangente.
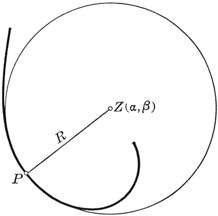
Cercle osculateur.
Cercle osculateur et courbure
On peut également définir le cercle osculateur de la courbe au point M comme le cercle « le plus proche possible » de M, au voisinage de M. On peut montrer que ce cercle embrasse mieux la courbe que ne le fait la tangente, d'où le mot osculateur (dont l'étymologie est « petite bouche »). Mais pour donner un sens précis à cette affirmation il faut introduire la notion de contact.
Le centre du cercle osculateur est appelé centre de courbure et son rayon le rayon de courbure. La courbure est, par définition, l'inverse du rayon de courbure. La courbure au point M est d'autant plus forte que la courbe effectue en M un virage serré.
Torsion d'une courbe gauche et généralisation
La tangente décrit bien le comportement de la courbe au premier ordre : la tendance globale de la courbe est d'avancer dans la direction de sa tangente. Le cercle osculateur et la courbure donnent un comportement de deuxième ordre, venant préciser l'information précédente, en donnant la tendance à tourner d'un côté ou de l'autre de la tangente.
Pour les courbes de l'espace à trois dimensions, il est possible d'aller plus loin. La courbe, à l'ordre deux, a tendance à avancer en tournant en restant dans le plan contenant le cercle osculateur (appelé plan osculateur). Une correction, d'ordre 3, vient s'ajouter, qui correspond à une tendance à s'écarter du plan osculateur. L'invariant correspondant est la torsion de la courbe. La torsion est donc ce qui fait que la courbe est non plane.
Il serait possible de poursuivre plus avant avec des courbes dans des espaces de dimension supérieure à trois, et une famille d'invariants généralisant courbure et torsion, et qui décrivent la courbe à des ordres d'approximation de plus en plus grands. Enfin, tous ces calculs, pour être réalisés, demandent la vérification d'un certain nombre de conditions de régularité des fonctions, et l'exclusion de points ayant un comportement exceptionnel.
Modes de définition d'une courbe plane
Il existe pour les courbes planes plusieurs modes d'introduction traditionnels. On se place ici dans le plan de la géométrie, muni d'un repère orthonormé . On fait l'hypothèse générale que les fonctions qui apparaissent sont dérivables. La raison de cette limitation apparaîtra un peu plus bas.
Équation paramétrique
Une courbe définie par une équation paramétrique est le lieu des points  , où
, où  et
et 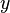 sont des fonctions d'un paramètre
sont des fonctions d'un paramètre  prenant ses valeurs dans une partie de
prenant ses valeurs dans une partie de 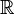
-
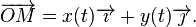
En un point où le vecteur dérivé
-
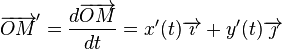
est non nul, il y a une tangente à la courbe, dirigée par ce vecteur.
L'interprétation cinématique classique est de considérer le paramètre t comme le temps, le vecteur dérivé est alors le vecteur vitesse.
Il convient alors de distinguer :
la courbe, qui est souvent appelée trajectoire, et qui est un sous-ensemble du plan ;
l'arc paramétré proprement dit qui est la courbe munie de sa « loi de temps », c'est-à-dire le couple de fonctions x(t),y(t).
Remarque : La représentation graphique d'une fonction y=f(x) peut être vue comme un cas particulier de courbe paramétrée : en prenant comme paramètre l'abscisse elle-même (t=x), on a x(t)=t, y(t)=f(t).
Équation polaire
On utilise pour ce type de courbe les coordonnées polaires. La courbe est alors définie par une fonction et ses points ont pour coordonnées polaires .
On peut facilement se ramener à une courbe paramétrée, d'équations . Mais les mathématiciens traitent ces courbes par des méthodes adaptées, en introduisant en premier lieu la notion de repère mobile.
Équation cartésienne
Étant donnée une fonction f de x et de y, on appelle courbe d'équation cartésienne f(x,y)=C l'ensemble des points M(x,y) dont les coordonnées vérifient cette équation.
On parle aussi pour cet ensemble de la ligne de niveau C de la fonction f. Si la fonction f représente une altitude, on retrouve le concept familier de courbe de niveau d'une carte de géographie.
Par exemple la ligne de niveau R>0 pour la fonction est le cercle de centre O et de rayon R.
Le théorème des fonctions implicites permet de trouver l'équation de la tangente à cette courbe en un point donné. Précisément, un point M=(x,y) appartenant à la courbe est dit régulier quand le gradient de f est non nul en ce point. Et dans ce cas, la tangente est orthogonale au vecteur gradient.
Équation intrinsèque
Il s'agit de décrire une courbe par une équation reliant exclusivement les invariants euclidiens : abscisse curviligne, rayon de courbure (ou courbure), rayon de torsion (ou torsion). Pour les courbes planes, l'invariant de torsion n'intervient pas. À la différence des systèmes précédents, de telles équations déterminent par nature les courbes indépendamment de leur orientation dans l'espace : les courbes sont donc définies à un déplacement près. Les équations les plus simples déterminent en général des courbes de type spirale.
(a donné) détermine une cycloïde ;
(a donné) détermine une clothoïde ;
(a donné) détermine une spirale logarithmique.
Définition des courbes gauches
On se place cette fois dans l'espace à trois dimensions usuel, muni d'un repère orthonormé  .
.
Équation paramétrique
L'équation paramétrique prend cette fois la forme
-
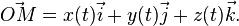
Le principe du calcul de la tangente est le même : en un point où le vecteur dérivé
-
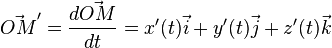
est non nul, il y a une tangente à la courbe, dirigée par ce vecteur.
Équations cartésiennes
Une équation de la forme F(x,y,z)=C définit un ensemble appelé surface de niveau de la fonction F. Sous certaines conditions, l'intersection de deux surfaces de niveau définit une courbe et permet le calcul de sa tangente.
Voici le détail de ces conditions pour l'intersection
-
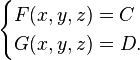
Si les fonctions F et G sont différentiables et que les vecteurs gradients de F et G en un point M de l'intersection sont des vecteurs indépendants, alors la courbe d'intersection possède une tangente dirigée par le vecteur
-
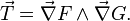
Avec les coniques, on a un exemple très classique d'introduction des courbes par intersection de surfaces : ce sont les courbes obtenues par intersection d'un cône de révolution et d'un plan.
Équation intrinsèque
Le principe est le même que pour les courbes planes, mais l'invariant de torsion peut intervenir. Par exemple, R le rayon de courbure et T le rayon de torsion, et (a, b donnés) déterminent une hélice circulaire.
Considérations topologiques
Lorsqu'on relâche l'exigence de dérivabilité des fonctions définissant les courbes, la situation peut singulièrement se compliquer.
Les trois premières étapes de la construction de la courbe de Peano.
Un exemple surprenant : la courbe de Peano
En 1890, Peano découvrit une « courbe » aux propriétés étranges :
elle est définie par une application continue de [0, 1] dans le plan ;
sa trajectoire est l'ensemble des points du carré [0, 1]×[0, 1].
L'illustration représente les premières étapes de la construction de cette courbe, qu'on range aujourd'hui dans la catégorie des fractales.
Avec cet exemple, ou en considérant d'autres constructions de courbes fractales telles que le flocon de Koch ou la courbe du dragon, la notion de dimension semble perdre de sa pertinence. Il est possible en effet que l'image du segment [0,1] par une application continue ait une dimension de Hausdorff strictement supérieure à 1, ou même une mesure de Lebesgue différente de 0.
Théorème de Jordan
Même dans le cadre très général des courbes continues, un résultat de topologie à l'énoncé apparemment élémentaire reste vérifié : une boucle délimite un intérieur et un extérieur.
Dit en termes moins vagues, si une courbe continue est fermée (les deux extrémités coïncident) et simple (la fonction est injective sur [a,b[, c'est-à-dire la courbe ne se recoupe pas elle-même) alors elle sépare le plan en deux composantes connexes, l'une bornée (l'intérieur), l'autre non bornée (l'extérieur). De plus la courbe est la frontière (au sens topologique) de chacune de ces deux parties.
Ce théorème ne connut une démonstration que tardivement (en 1905, par Oswald Veblen) après plusieurs tentatives incomplètes. Il convient de noter que la courbe de Peano n'est pas une courbe simple, même si les fonctions obtenues à chaque étape de sa construction le sont.
Exemple de nœud.
Plongement, nœud
Soit I un intervalle. L'application est appelée plongement lorsqu'elle réalise un homéomorphisme de I sur son image f(I). De même on parle de courbe fermée plongée pour une application définie sur le cercle unité et qui constitue un homéomorphisme sur son image.
Il est possible de plonger le cercle de plusieurs façons, non équivalentes, dans l'espace de dimension trois. La classification des plongements possibles constitue la théorie des nœuds.
Courbes algébriques

Un exemple de sextique du plan.
Une courbe du plan est dite algébrique si son équation cartésienne est polynomiale. Le plus grand degré (somme des degrés en x et en y) de l'équation cartésienne est appelé le degré de la courbe. Par exemple, la courbe ci-contre a pour équation cartésienne , le premier terme est de degré 2 + 4 = 6, et tous les autres termes sont de degré inférieur à 6. C'est donc une courbe de degré 6, ou sextique.
Selon son degré, une courbe algébrique du plan est :
une droite si elle est de degré 1 ;
une conique si elle est de degré 2 ;
une courbe cubique si elle est de degré 3 ;
une quartique si elle est de degré 4 ;
une quintique si elle est de degré 5 ;
etc.
Une courbe algébrique sur le corps des complexes est une surface de Riemann; dans ce cas,elle est topologiquement équivalente à un tore à g trous ; l’entier g est appelé le genre (mathématiques) de la courbe. Le genre dépend du degré et des points singuliers de la courbe. Par exemple, une courbe elliptique (qui est une cubique sans singularité) de est de genre 1, mais une cubique admettant un point singulier est de genre 0.
Lorsqu'elle est unicursale, une courbe algébrique admet une représentation paramétrique.
Dans l'espace, une équation cartésienne polynomiale en x, y et z décrit une surface algébrique. Une courbe algébrique de l'espace est alors définie comme une intersection de surfaces algébriques. Par exemple, l'intersection de deux quadriques est en général formée de deux coniques disjoints. L'étude de ces objets, et donc en particulier des courbes algébriques, est la géométrie algébrique.

 词典释义:
词典释义:
 的, 弯
的, 弯 的
的
 ,
, 
 ; 图表
; 图表
 ; [数]几何
; [数]几何
 形
形 的
的
 +e
+e
 ,圆,环
,圆,环
 ,使弯下;使倾斜
,使弯下;使倾斜 ,
, 形;
形; ;
; 的;
的; 化;
化; ,垂直
,垂直 ;
;
 的courbef
的courbef
 ; 图;
; 图; 
 图
图

 近[
近[ ]
]






 图
图







 , 航迹包
, 航迹包

 拟合
拟合
 拟合
拟合 杆
杆 图
图
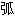 微分
微分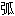 齿圆锥齿轮
齿圆锥齿轮
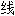 修匀
修匀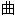
 斜率
斜率
 板; 云形规
板; 云形规 面
面
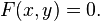


 , où
, où  et
et 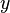 sont des fonctions d'un paramètre
sont des fonctions d'un paramètre  prenant ses valeurs dans une partie de
prenant ses valeurs dans une partie de 
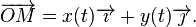
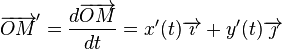
 .
.