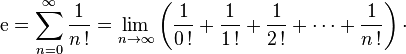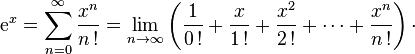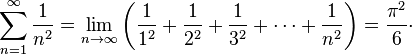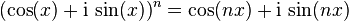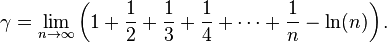Leonhard Euler ( audio), né le 15 avril 1707 à Bâle (Suisse) et mort à 76 ans le 18 septembre (7 septembre) 1783 à Saint-Pétersbourg (Empire russe), est un mathématicien et physicien suisse, qui passa la plus grande partie de sa vie dans l'Empire russe et en Allemagne. Il était notamment membre de l'Académie royale des sciences de Prusse à Berlin.

Euler fit d'importantes découvertes dans des domaines aussi variés que le calcul infinitésimal et la théorie des graphes. Il introduisit également une grande partie de la terminologie et de la notation des mathématiques modernes, en particulier pour l'analyse mathématique, comme la notion de fonction mathématique. Il est aussi connu pour ses travaux en mécanique, en dynamique des fluides, en optique et en astronomie.

Euler est considéré comme un éminent mathématicien du XVIII siècle et l'un des plus grands et des plus prolifiques de tous les temps. Une déclaration attribuée à Pierre-Simon de Laplace exprime l'influence d'Euler sur les mathématiques : « Lisez Euler, lisez Euler, c'est notre maître à tous ». Il était un fervent chrétien, croyant en l'inerrance biblique, et s'opposa avec force aux athées éminents de son temps.

Biographie

Premières années

Ancien billet de 10 francs suisses, honorant Euler

Leonhard Euler naquit à Bâle de Paul Euler, pasteur des Églises réformées et de Marguerite Brucker, fille de pasteur. Il eut deux jeunes sœurs du nom d'Anna Maria et de Maria Magdalena. Peu de temps après la naissance de Leonhard, la famille Euler déménagea de Bâle pour rejoindre la ville voisine de Riehen, où Euler passa la plus grande partie de son enfance. Paul Euler était un ami de la famille Bernoulli — Jean Bernoulli, alors considéré comme le principal mathématicien européen, pourrait être celui ayant eu la plus grande influence sur le jeune Leonhard. L'éducation officielle d'Euler commença tôt à Bâle, où il fut envoyé vivre avec sa grand-mère maternelle. À l'âge de treize ans, il s'inscrivit à l'université de Bâle, et en 1723 obtint sa maîtrise de philosophie (Magister Philosophiae), grâce à une dissertation qui comparait la philosophie de Descartes à celle de Newton. À cette époque, il recevait tous les samedis après-midi des leçons de Jean Bernoulli, qui découvrit rapidement chez son nouvel élève un incroyable talent pour les mathématiques. Euler commença alors à étudier la théologie, le grec et l'hébreu à la demande de son père, afin de devenir pasteur, mais Jean Bernoulli convainquit Paul Euler que Leonhard était destiné à devenir un grand mathématicien. En 1727, il participa au concours de l'Académie des sciences de Paris qui consistait à résoudre un problème scientifique. Cette année-là, le problème était de trouver la meilleure façon de placer les mâts d'un navire. Euler remporta la deuxième place, derrière Pierre Bouguer, qui est maintenant connu comme le « père de l'architecture navale ». Par la suite, Euler gagna ce prestigieux prix annuel douze fois dans sa carrière.

Saint-Pétersbourg

À cette époque, les deux fils de Jean Bernoulli, Daniel et Nicolas, travaillaient à l'Académie des sciences de Russie à Saint-Pétersbourg. En juillet 1726, Nicolas mourut de l'appendicite, après avoir passé un an en Russie, et quand Daniel reprit les positions de son frère en mathématiques et en physique, il recommanda que le poste en physiologie qu'il avait laissé vacant fût comblé par son ami Leonhard Euler. En novembre 1726, Euler accepta l'offre avec empressement, mais fit le voyage à Saint-Pétersbourg avec retard, après avoir postulé en vain à un poste de professeur de physique à l'université de Bâle.

Timbre de 1957 de l'ex-Union soviétique commémorant le 250 anniversaire d'Euler

Euler arriva dans la capitale russe le 17 mai 1727. Occupant d'abord un poste au département médical de l'académie, il fut ensuite affecté au département de mathématiques. Il logeait auprès de Daniel Bernoulli, avec qui il travaillait souvent en étroite collaboration. Euler maîtrisait le russe et s'installa à Saint-Pétersbourg. Il prit également un emploi additionnel de médecin dans la marine russe.

Créée par Pierre le Grand, l'Académie de Saint-Pétersbourg était destinée à améliorer l'éducation en Russie et à combler le retard scientifique qui la séparait de l'Europe occidentale. En conséquence, elle était particulièrement intéressante pour les étudiants étrangers comme Euler. L'académie possédait suffisamment de ressources financières et une bibliothèque complète tirée de la bibliothèque privée de Pierre le Grand et de la noblesse russe. Très peu d'étudiants étaient inscrits dans l'Académie, de façon à diminuer la charge des professeurs, à mettre l'accent sur la recherche et à offrir à son corps professoral à la fois le temps et la liberté d'effectuer des recherches scientifiques.

Catherine I de Russie, qui poursuivait la politique de son défunt mari, décéda le jour de l'arrivée d'Euler. La noblesse russe prit alors le pouvoir lors de l'ascension de Pierre II de Russie, âgé de douze ans. La noblesse se méfiait des chercheurs étrangers ; elle réduisit le financement et causa d'autres difficultés à Euler et à ses collègues. Leurs conditions de travail s'améliorèrent légèrement à la mort de Pierre II ; Euler put donc rapidement gravir les échelons dans l'Académie, jusqu'à devenir professeur de physique en 1731. Deux ans plus tard, Daniel Bernoulli, lassé de la censure et de l'hostilité dont il faisait l'objet à Saint-Pétersbourg, partit pour Bâle. Euler lui succéda alors à la tête du département de mathématiques.

Le 7 janvier 1734, il épousa Katharina Gsell (1707-1773), fille du peintre Georg Gsell. Le jeune couple acheta une maison sur la Neva. De leurs treize enfants, cinq seulement atteignirent l'âge adulte. Leonhard Euler, après le décès de Katharina Gsell en 1773, épouse l'année suivante une demi-sœur de celle-ci, Salomé Abigail Gsell (1723-1794), fille de Dorothea Graff (1678-1743) et de Georg Gsell (1673-1740). Dorothea Graff, fille de Maria Sibylla Merian était comme elle peintre et naturaliste, et avait accompagné sa mère dans ses expéditions au Surinam. Son mari, Georg Gsell, peintre et marchand d'art, recruté par Pierre le Grand en 1716, devint conservateur de la Kunstkamera).

Berlin

Timbre de RDA commémorant le 200 anniversaire de la mort d'Euler

Préoccupé par la persistance des troubles en Russie, Euler quitta Saint-Pétersbourg le 19 juin 1741 pour occuper un poste à l'Académie de Berlin, qui lui était proposé par Frédéric II de Prusse. Il vécut pendant vingt-cinq ans à Berlin, où il écrivit plus de 380 articles. À Berlin, il publia deux célèbres ouvrages : l'Introductio in analysin infinitorum (« Introduction à l’analyse des infiniment petits »), un texte sur les fonctions publié en 1748 et Institutiones calculi differentialis (« Traité du calcul différentiel »), publié en 1755 et traitant du calcul différentiel.

En outre, Euler fut invité à être le professeur de la princesse d'Anhalt-Dessau, la nièce de Frédéric II. Euler lui écrivit plus de 200 lettres, qui furent ensuite rassemblées dans un best-seller intitulé Lettres à une princesse d'Allemagne (en) sur divers sujets de physique et de philosophie. Cet ouvrage contient des publications d'Euler sur divers sujets se rapportant à la physique et aux mathématiques, mais également sur des sujets philosophiques. Ce livre est devenu le plus largement lu de tous ses travaux mathématiques, et il a été publié en Europe et aux États-Unis. La popularité des « Lettres » témoigne de la capacité d'Euler à communiquer efficacement sur les questions scientifiques au public, une capacité rare pour un chercheur scientifique.

Malgré l'immense contribution d'Euler au prestige de l'Académie, il fut finalement contraint de quitter Berlin, en partie à cause d'un conflit de personnalité avec Frédéric II. En effet, le monarque avait moins de considération pour Euler que pour son cercle de philosophes. Voltaire faisait partie de ceux qui étaient aux côtés de Frédéric II, et il eut une bonne place dans le cercle du roi. Euler, simple homme religieux et travailleur acharné, était très classique dans ses convictions et ses goûts. Il fut, à bien des égards, l'opposé de Voltaire. Euler avait une formation limitée en rhétorique, et avait tendance à débattre sur des questions qu'il connaissait peu, faisant de lui une cible fréquente de l'esprit de Voltaire. Frédéric II exprima également sa déception vis-à-vis des capacités d'ingénierie d'Euler :

« Je voulais avoir un jet d'eau dans mon jardin : Euler a calculé la force des roues nécessaire afin d'élever l'eau jusqu'à un réservoir, d'où elle doit redescendre à travers des canaux, pour enfin sortir de la fontaine. Mon moulin a été réalisé géométriquement mais ne peut pas élever une goutte d'eau à moins de cinquante pas du réservoir. Vanité des vanités ! Vanité de la géométrie ! »

Déclin de la vue

Portrait de 1753 par Emanuel Handmann. Cette représentation indique des problèmes de la paupière droite et un possible strabisme. L'œil gauche semble en bonne santé, mais il a plus tard été affecté par une cataracte.

La vue d'Euler empira tout au long de sa carrière en mathématiques. Trois ans après avoir souffert d'une fièvre quasi mortelle en 1735, il devint presque aveugle de l'œil droit. Euler attribua plutôt son état au travail minutieux qu'il avait effectué en cartographie pour l'Académie de Saint-Pétersbourg. La vue d'Euler de l'œil droit empira tout au long de son séjour en Allemagne, si bien que Frédéric II le surnommait « Cyclope ». Euler souffrit ensuite d'une cataracte de l'œil gauche, le rendant presque totalement aveugle. Il semble que ce mauvais état ait eu peu d'effet sur sa productivité, Euler ayant compensé son handicap par ses compétences en calcul mental et par sa mémoire eidétique. Par exemple, Euler pouvait répéter l'Énéide de Virgile, du début à la fin, sans hésitation, et pour chaque page de son édition, il pouvait citer la première ligne et la dernière. Avec l'aide de ses scribes, la productivité d'Euler dans de nombreux domaines d'étude augmenta en fait. Ainsi, il produisit en moyenne un document de mathématiques par semaine au cours de l'année 1775.

Retour en Russie

La tombe de Leonhard Euler au monastère Alexandre-Nevski.

La situation en Russie s'était grandement améliorée depuis l'accession au trône de Catherine II de Russie ; en 1766, Euler accepta une invitation à revenir à l'Académie de Saint-Pétersbourg. C'est ainsi qu'il passa le reste de sa vie en Russie. Son second séjour dans le pays fut cependant marqué par la tragédie. Un incendie à Saint-Pétersbourg en 1771 lui coûta son domicile, et faillit lui ôter la vie. En 1773, il perdit son épouse de 40 ans. Trois ans après la mort de sa femme, Euler se remaria avec la demi-sœur de celle-ci, Salomé Abigail Gsell (1723-1794). Ce mariage allait durer jusqu'à sa mort.

Le 18 septembre 1783, Euler décéda à Saint-Pétersbourg d'une hémorragie intra-cérébrale et fut enterré avec son épouse au cimetière luthérien de Smolensk sur l'île Vassilievski (au XX siècle le cimetière a été fermé, les restes d'Euler ont été transférés au cimetière Saint-Lazare du monastère Alexandre-Nevski). Son éloge funèbre fut écrit pour l'Académie française par le mathématicien et philosophe français Nicolas de Condorcet. Le récit de sa vie, avec une liste de ses œuvres, fut écrit par Nikolaus von Fuss, le beau-fils d'Euler et le secrétaire de l'Académie des sciences de Russie. Condorcet écrit dans son Éloge : « … il cessa de calculer et de vivre ».

Contributions aux mathématiques

Leonhard Euler a travaillé dans presque tous les domaines des mathématiques : la géométrie, le calcul infinitésimal, la trigonométrie, l'algèbre et la théorie des nombres. Il est une figure capitale de l'histoire des mathématiques : s'ils étaient imprimés, ses écrits, dont beaucoup sont d'un intérêt fondamental, pourraient occuper entre quarante et soixante ouvrages. Le nom d'Euler est associé à un grand nombre de sujets.

Notation mathématique

Euler a introduit et popularisé plusieurs conventions de notation par le biais de ses nombreux ouvrages largement diffusés. Plus particulièrement, il a introduit la notion de fonction et a été le premier à écrire pour désigner la fonction appliquée à l'argument , en 1734. Il a également introduit la notation moderne des fonctions trigonométriques, la lettre e pour la base du logarithme naturel (également connue sous le nom de nombre d'Euler) en 1727, la lettre grecque Σ pour désigner une somme en 1755 et la lettre i pour représenter l'unité imaginaire, en 1777. L'utilisation de la lettre grecque π pour désigner le rapport de la circonférence d'un cercle à son diamètre a également été popularisée par Euler, mais celui-ci n'est pas à l'origine de la notation.

Analyse

Le développement du calcul infinitésimal a été au premier plan des recherches mathématiques du XVIII siècle, et la famille Bernoulli — amis d'Euler — est à l'origine de nombreux progrès dans ce domaine. Grâce à leur influence, l'étude du calcul infinitésimal est devenu l'un des axes principaux du travail d'Euler. Bien que certaines des démonstrations d'Euler ne soient pas acceptables au regard des normes modernes de rigueur mathématique, ses idées ont tout de même conduit à de grandes avancées.

Euler est bien connu dans le domaine de l'analyse pour son usage fréquent des séries numériques et des séries entières. Il a notamment montré que le nombre est la somme de la série de terme général :

Il a trouvé le « développement en série entière » de la fonction exponentielle :

et celui de la fonction arc tangente.

Sa ténacité à utiliser les développements en séries lui a permis de résoudre le fameux problème de Bâle en 1735 :

Euler est pleinement conscient de la nécessité de démontrer rigoureusement les résultats de convergence dont il se sert, mais cela ne l'empêche pas d'écrire également des formules « paradoxales » telle que , de définir des règles d'emploi et de calcul avec de telles séries divergentes, et de les utiliser pour obtenir des résultats inattendus concernant, par exemple, la fonction zêta.

Une interprétation géométrique de la formule d'Euler

Euler a introduit l'utilisation de la fonction exponentielle et des logarithmes dans les démonstrations en analyse. Il a découvert des moyens d'exprimer différentes fonctions logarithmiques en utilisant les séries entières, et il a étendu la notion de logarithme aux nombres négatifs et aux nombres complexes. Il a également défini la fonction exponentielle pour les nombres complexes, et a découvert la relation qui la lie aux fonctions trigonométriques :

pour tout réel ,

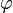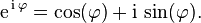
Un cas particulier de cette « formule d'Euler », obtenu en donnant à la valeur est

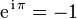, qu'on préfère souvent écrire :

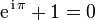
formule connue sous le nom d'identité d'Euler, et qualifiée de « formule la plus remarquable des mathématiques » par Richard Feynman, car elle réunit en seulement 7 caractères l'addition, la multiplication, l'exponentiation, l'égalité et les constantes remarquables 0, 1, , et . En 1988, les lecteurs de The Mathematical Intelligencer l'ont désignée comme « la plus belle formule mathématique de tous les temps ». Au total, le nom d'Euler figurait dans trois des cinq formules arrivées en tête de ce vote.

La formule de De Moivre

est une conséquence directe de la formule d'Euler.

En outre, Euler a contribué à la théorie des fonctions transcendantes avec l'introduction de la fonction bêta et de la fonction gamma. Il a également introduit une nouvelle méthode pour résoudre les équations quartiques. Il a aussi trouvé une façon de calculer des intégrales avec des limites complexes, préfigurant le développement moderne de l'analyse complexe, et a inventé le calcul des variations, qui inclut l'un de ses résultats les plus célèbres, nommé l'équation d'Euler-Lagrange.

Euler fut le pionnier de l'utilisation de méthodes d'analyse pour résoudre des problèmes de la théorie des nombres. Ce faisant, il a réuni deux branches différentes des mathématiques et introduit un nouveau champ d'étude : la théorie analytique des nombres. Euler a aussi introduit la théorie des séries hypergéométriques, des fonctions hyperboliques et la théorie analytique des fractions continues. Par exemple, il a prouvé l'infinité des nombres premiers en utilisant la divergence de la série harmonique, et il a utilisé les méthodes analytiques pour avoir une meilleure compréhension de la répartition des nombres premiers. Les travaux d'Euler dans ce domaine ont contribué à l'élaboration du théorème des nombres premiers.

Théorie des nombres

L'intérêt d'Euler dans la théorie des nombres peut être attribué à l'influence de Christian Goldbach, son ami à l'Académie de Saint-Pétersbourg. Un grand nombre des premiers travaux d'Euler en théorie des nombres est fondé sur les travaux de Pierre de Fermat. Euler a développé quelques idées de Fermat, et a réfuté certaines de ses conjectures.

Euler a fait le lien entre la distribution des nombres premiers et l'analyse. Il a démontré que la série des inverses des nombres premiers diverge. Pour ce faire, il a découvert le lien entre la fonction zêta de Riemann et les nombres premiers.

Euler a démontré les identités de Newton, le petit théorème de Fermat, le théorème des deux carrés de Fermat, et il a également travaillé sur le théorème des quatre carrés de Lagrange. Il a aussi défini la fonction qui associe à tout entier le nombre d'entiers positifs inférieurs à et qui sont premiers avec En utilisant les propriétés de cette « indicatrice », il a généralisé le petit théorème de Fermat pour aboutir à ce qui est maintenant connu sous le nom de théorème d'Euler. Il a contribué de manière significative à la recherche sur les nombres parfaits, qui ont fasciné les mathématiciens depuis Euclide. Euler a également conjecturé la loi de réciprocité quadratique. Cet énoncé est considéré comme un théorème fondamental de la théorie des nombres, et en cela Euler a ouvert la voie aux travaux de Carl Friedrich Gauss.

En 1772, Euler a démontré que 2 147 483 **7 est un nombre de Mersenne premier. Il est resté le plus grand nombre premier connu jusqu'en 1867.

Géométrie

Comme dans les autres domaines des mathématiques, les contributions d'Euler à la géométrie sont exceptionnelles : angles d'Euler, droite d'Euler, cercle d'Euler, relation entre cercle inscrit et circonscrit, etc.

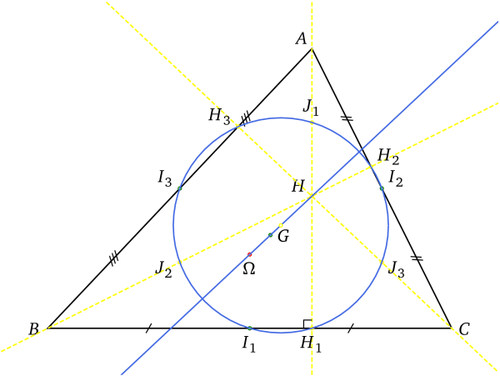
À titre d'exemple, il a montré que, pour tout triangle, les neuf points suivants :

les pieds des trois hauteurs (H1 H2 H3 dans le diagramme)

les milieux des trois côtés (I1 I2 I3 dans le diagramme)

les milieux de chacun des segments reliant l'orthocentre aux sommets du triangle (J1 J2 J3 dans le diagramme)

sont situés sur un même cercle. Ce « cercle des neuf points » est encore appelé « cercle d'Euler » associé au triangle.

Il a démontré aussi que, dans tout triangle, l'orthocentre, le centre du cercle circonscrit, le centre de gravité et le centre du cercle des neuf points sont alignés. La droite qui les porte est appelée « droite d'Euler » associée au triangle.

Théorie des graphes

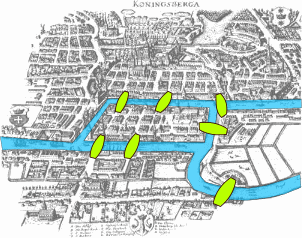
En 1736, Euler résolut le problème des sept ponts de Königsberg. La ville de Königsberg, en Prusse, est traversée par la rivière Pregolia, qui entoure deux grandes îles reliées entre elles et aux deux rives par sept ponts. Le problème était de savoir s'il est possible de suivre un chemin qui emprunte chaque pont une fois et une seule et revienne au point de départ. Euler a établi que, pour que ce soit possible, il aurait fallu que chacune des quatre zones géographiques (les deux îles et les deux rives) soit atteinte par un nombre pair de ponts — en termes modernes : que chacun des quatre « sommets » du « graphe » soit adjacent à un nombre pair d'« arêtes » (un graphe ayant cette propriété est dit « eulérien »). La résolution de ce problème est considérée comme le premier théorème de la théorie des graphes.

Euler a également établi la formule liant le nombre de sommets, d'arêtes et de faces d'un polyèdre convexe, et donc d'un graphe planaire. La constante de cette formule est maintenant connue comme la caractéristique d'Euler pour un graphe (ou pour un autre objet mathématique), et est liée au genre de l'objet. L'étude et la généralisation de cette formule, notamment par Cauchy et L'Huillier, est à l'origine de la topologie.

En outre, Leonhard Euler est le premier à avoir étudié le problème du cavalier, en 1759. Il publiera ses recherches sur la question dans « Solution d'une question curieuse qui ne paraît soumise à aucune analyse ».

Mathématiques appliquées

Certains des plus grands succès d'Euler ont été dans la résolution des problèmes analytiques dans des domaines autres que les mathématiques et dans la description de nombreuses applications des nombres de Bernoulli, des séries de Fourier, des diagrammes de Venn, des nombres d'Euler, des constantes e et π, des fractions continues et des intégrales. Il a développé des outils qui rendent plus faciles à appliquer certains problèmes physiques. Il a fait progresser le domaine de l'amélioration de l'approximation numérique d'intégrales, en inventant ce qui est maintenant connu sous le nom de méthode d'Euler. Euler a également démontré, en même temps que l'écossais Colin Maclaurin — mais bien indépendamment — la formule d'Euler-Maclaurin. Il a aussi facilité l'utilisation des équations différentielles, en particulier en introduisant la constante d'Euler-Mascheroni :

Un des domaines les moins communs qui intéressaient Euler était l'application des idées mathématiques à la musique. En 1739, il écrivit Tentamen novae theoriae musicae, dans l'espoir de finalement intégrer la théorie musicale aux mathématiques. Cette partie de son travail, cependant, n'a pas reçu une grande attention et a été décrite comme trop mathématique pour les musiciens mais aussi trop musicale pour les mathématiciens. On y trouve cependant le tout premier exemple de théorie des graphes avec une disposition des notes couramment utilisée de nos jours en analyse musicale, le Tonnetz, mieux développé dans De harmoniae veris principiis per speculum musicum repraesentatis en 1774.

Autres sciences

Leonhard Euler a également contribué à d'autres sciences, comme certains domaines des sciences physiques, en étudiant par exemple le mouvement de la Lune.

Physique et astronomie

Euler a contribué à l'élaboration de la théorie d'Euler-Bernoulli, qui est un modèle utilisé dans le domaine de la résistance des matériaux. En dehors de l'application avec succès de ses outils d'analyse aux problèmes liés à la mécanique newtonienne, Euler a également appliqué ses techniques à des problèmes d'astronomie. Ses travaux dans cette science ont été reconnus par un certain nombre de prix décernés par l'Académie de Paris au cours de sa carrière. Ses réalisations comprennent la détermination avec une grande précision des orbites des comètes et des autres corps célestes, mais aussi la compréhension de la nature des comètes, et le calcul de la parallaxe du Soleil. Ses calculs ont également contribué à l'élaboration de tables précises de longitudes.

En dynamique des fluides, Euler fut le premier à poser les équations désormais connues sous le nom d'équations d'Euler des fluides parfaits, dans « Mémoires de l'Académie royale des sciences et des belles lettres de Berlin » (1757). Elles permettent le calcul de nombreux écoulements, comme la circulation sanguine, l'aérodynamique des automobiles et des avions, l'hydraulique, l'océanographie, la météorologie ou la grande tache rouge de Jupiter.

En outre, Euler a fait d'importantes contributions en optique. Il a exprimé son désaccord avec la théorie corpusculaire de la lumière de Newton dans Opticks, qui était alors la théorie dominante. Ses documents des années 1740 sur l'optique ont contribué à faire en sorte que la théorie ondulatoire de la lumière proposée par Christian Huygens devienne la théorie la plus largement répandue, au moins jusqu'au développement de la théorie quantique de la lumière.

Logique

Il est aussi crédité pour avoir, avec l'aide des courbes fermées, illustré le raisonnement syllogistique, en 1768. Ces schémas sont désormais connus sous le nom de diagrammes d'Euler. Ainsi, le diagramme de gauche illustre le syllogisme suivant :

Illustration d'un syllogisme de la deuxième figure par un diagramme d'Euler. Aucun prêtre n'est un singe. Or, les chimpanzés sont des singes. Donc, les chimpanzés ne sont pas prêtres.

Philosophie personnelle et croyances religieuses

Leonhard Euler et son ami Daniel Bernoulli ont été des adversaires de la Monadologie de Leibniz et de la philosophie de Christian Wolff. Euler a insisté sur le fait que la connaissance est fondée en partie sur la base de lois quantitatives précises. Les tendances religieuses d'Euler pourraient aussi avoir eu une incidence sur son aversion de la doctrine, il est allé jusqu'à qualifier les idées de Wolff de « sauvages et athées ».

Beaucoup de ce qui est connu des croyances religieuses d'Euler peut être déduit de ses Lettres à une princesse d'Allemagne sur divers sujets de physique et de philosophie et d'un ouvrage antérieur, Rettung der Göttlichen Offenbahrung Gegen die Einwürfe der Freygeister. Ces écrits montrent qu'Euler était un fervent chrétien qui estimait que la Bible avait été inspirée.

Une anecdote rapportée par Dieudonné Thiébault met en scène les croyances religieuses d'Euler. Le philosophe français Denis Diderot, en visite à Saint-Pétersbourg en 1773-1774, avait accepté, à la demande de l'impératrice Catherine II, de voir la preuve de l'existence de Dieu qu'Euler prétendait pouvoir produire. Les deux hommes se rencontrèrent donc et Euler, sur un ton d'une parfaite conviction annonça « Monsieur, (a + b)/n = x ; donc Dieu existe, répondez ! » . Le désarroi de Diderot, pour qui, (selon l'anecdote) les mathématiques étaient incompréhensibles, provoqua les rires de la cour. Gêné, il demanda à quitter la Russie. Il est plus que probable que l'anecdote soit apocryphe et Thiébault ne prétend pas le contraire. De toute évidence, ce dernier n'était pas présent, ses mémoires sont tardifs, la formule soi-disant donnée par Euler n'a aucun sens et Diderot n'était pas étranger aux mathématiques – comme en atteste la réputation qu'il s'était faite avec ses Mémoires sur différents sujets de mathématiques entre autres.

Publications

La couverture de Methodus inveniendi lineas curvas, écrit par Euler

Leonhard Euler a beaucoup écrit. Ses ouvrages les plus connus sont :

Éléments d'algèbre (en) — Cet ouvrage d'algèbre élémentaire commence par une discussion sur la nature des nombres et donne une introduction à l'algèbre, incluant les formules pour les solutions d'équations polynomiales. Écrit en 1765 en allemand sous le titre Vollständige Anleitung zur Algebra, traduction en russe publiée en 1770 par l'Académie des sciences de Saint-Pétersbourg, puis : 1 éd. en allemand en 1770, en 2 volumes ; vol. 1 : E387, vol. 2 : E388 ou ; traduit en français : en 1774 par Jean III Bernoulli, en 1807 par Jean-Guillaume Garnier : vol. 1 et 2 ; traduit en anglais (à partir des versions en français) : en 1797 par Francis Horner (2 éd. : Johnson, 1810), incluant la traduction des Additions de 1774 par Lagrange, aperçu sur Google Livres, en 1822 par John Hewlett, éd. Longman, aperçu sur Google Livres, en 1824 par Charles Tayler.

1 éd. en allemand en 1770, en 2 volumes ; vol. 1 : E387, vol. 2 : E388 ou ;

traduit en français : en 1774 par Jean III Bernoulli, en 1807 par Jean-Guillaume Garnier : vol. 1 et 2 ;

en 1774 par Jean III Bernoulli,

en 1807 par Jean-Guillaume Garnier : vol. 1 et 2 ;

traduit en anglais (à partir des versions en français) : en 1797 par Francis Horner (2 éd. : Johnson, 1810), incluant la traduction des Additions de 1774 par Lagrange, aperçu sur Google Livres, en 1822 par John Hewlett, éd. Longman, aperçu sur Google Livres, en 1824 par Charles Tayler.

en 1797 par Francis Horner (2 éd. : Johnson, 1810), incluant la traduction des Additions de 1774 par Lagrange, aperçu sur Google Livres,

en 1822 par John Hewlett, éd. Longman, aperçu sur Google Livres,

en 1824 par Charles Tayler.

Introductio in analysin infinitorum, Marcum-Michaelem Bousquet & socios, 1748, Livre I : (ISBN 0387968245), Livre II : (ISBN 0387971327)

Lettres à une Princesse d'Allemagne, Barthelemy Chirol, Genève, 1775

Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici latissimo sensu accepti, 1744 ; le titre latin se traduit par « Une méthode pour trouver des lignes courbes jouissant de propriétés de maximum ou de minimum, ou la solution de problèmes isopérimétrique dans le sens le plus large ».

Une collection définitive des travaux d'Euler, nommée Opera Omnia, a été publiée en 1911 par la Commission Euler (de) de l'Académie suisse des sciences naturelles.

Hommages et distinctions

Euler est représenté sur la sixième série des billets suisses de 10 francs, sur de nombreux timbres postaux suisses, allemands et russes.

L'astéroïde (2002) Euler a été nommé en son honneur.

Euler est également honoré par l'Église luthérienne dans son calendrier des saints, le 24 mai.

莱昂哈德·欧拉（Leonhard Euler，**旧译欧拉，1707年4月15日－1783年9月18日）是一位瑞士数学家和物理学家，近代数学先驱之一，他一生大部分时间在俄国和普鲁士度过。

欧拉在数学的多个领域，包括微积分和图论都做出过重大发现。他引进的许多数学术语和书写格式，例如函数的记法"f(x)"，一直沿用至今。此外，他还在力学、光学和天文学等学科有突出的贡献。

欧拉是18世纪杰出的数学家，同时也是有史以来最伟大的数学家之一。他也是一位多产作者，其学术著作约有60-80册。法国数学家皮埃尔-西蒙·拉普拉斯曾这样评价欧拉对于数学的贡献：“读欧拉的著作吧，在任何意义上，他都是我们的大师”。

生平

早年 第六版10元瑞士法郎正面的欧拉肖像 欧拉出生于瑞士巴塞尔的一个牧师家庭，父亲保罗·欧拉（Paul Euler）是基督教加尔文宗的牧师，保罗·欧拉早年在巴塞尔大学学习神学，后娶了一位牧师的女儿玛格丽特·布鲁克（Marguerite Brucker），也就是欧拉的母亲。欧拉是他们6个孩子中的长子。在欧拉出生后不久，他们全家就从巴塞尔搬迁至郊外的里恩,在那里欧拉度过了他童年的大部分时光。 欧拉最早是从他的父亲那里接触到一些数学，后来欧拉搬回巴塞尔和他的外祖母住在一起，并在那里开始了他的正式学业，在中学时期，由于欧拉所在的学校并不教授数学，他便私下里从一位大学生那里学习。 欧拉13岁时进入了巴塞尔大学，主修哲学和法律，但在每周星期六下午便跟当时欧洲最优秀的数学家约翰·伯努利（Johann Bernoulli）学习数学 。欧拉于1723年取得了他的哲学硕士学位，学位论文的内容是笛卡尔哲学和牛顿哲学的比较研究。之后，欧拉遵从了他父亲的意愿进入了神学系，学习神学，希腊语和希伯来语（欧拉的父亲希望欧拉成为一名牧师），但最终约翰·伯努利说服欧拉的父亲允许欧拉学习数学，并使他相信欧拉注定能成为一位伟大的数学家。1726年，欧拉完成了他的博士学位论文De Sono，内容是研究声音的传播。1727年，欧拉参加了法国科学院主办的有奖征文竞赛，当年的问题是找出船上的桅杆的最优放置方法。结果他得了二等奖，一等奖为被誉为“舰船建造学之父”的皮埃尔·布格（Pierre Bouguer）所获得，不过欧拉随后在他一生中一共12次赢得该奖项一等奖。 在圣彼得堡 这一时期，约翰·伯努利的两个儿子——丹尼尔·伯努利和尼古拉·伯努利（Nicolas Bernoulli）——在位于俄国圣彼得堡的俄国皇家科学院工作，在尼古拉因阑尾炎于1726年7月去世后（此时距他来到俄国仅一年），丹尼尔便接替了他在数学/物理学所的职位，同时推荐欧拉来接替他自己在生理学所空出的职位。欧拉于1726年11月欣然接受了邀请，但并没有立即动身前往圣彼得堡，而是先申请巴塞尔大学的物理学教授，不过没有成功。 前苏联于1957年发行的邮票，纪念欧拉诞辰250周年。文本内容为：欧拉，伟大的数学家和学者，诞辰250周年。 欧拉于1727年5月17日抵达圣彼得堡，在丹尼尔等人的请求下，科学院将欧拉指派到数学/物理学所工作，而不是起初的生理学所。欧拉与丹尼尔保持着密切的合作关系，并且与丹尼尔住在一起。在1727年至1730年间，欧拉还担任了俄国海军医官的职务。 俄国皇家科学院由彼得大帝于1724年创建，在彼得大帝和他的继任者凯瑟琳女皇主政时期，科学院是一个对外国学者具有吸引力的地方。科学院有充足的资金来源和一个规模庞大的综合图书馆，并且只招收非常少的学生，以减轻教授们的教学负担。科学院还非常重视研究，给予教授们充分的时间及自由，让他们探究科学问题 。 凯瑟琳女皇，同时也是科学院的资助者，于欧拉到达圣彼得堡的当天去世。其后彼得二世继位，彼得二世是个软弱的君主，实际权力由俄国贵族掌握。贵族们对科学院的外国科学家心存戒心，于是他们切断了对欧拉及其同事们的财政资助，并且在其它方面找他们的麻烦。 情况在彼得二世去世（1730年）后有所好转，欧拉在科学院的地位迅速得到提升，并于1731年获得物理学教授的职位。两年后，由于受不了在圣彼得堡受到的种种审查和敌视，丹尼尔·伯努利返回了巴塞尔，欧拉于是接替丹尼尔成为数学所所长 。1735年，欧拉还在科学院地理所担任职务，协助编制俄国第一张全境地图。 1734年1月7日，欧拉迎娶了科学院附属中学的美术教师，瑞士人乔治·葛塞尔（Georg Gsell）的女儿，柯黛琳娜·葛塞尔（Katharina Gsell，1707-1773） ，两人共育有13个子女，其中仅有5个活到成年 。 在柏林 前东德发行的欧拉逝世200周年纪念邮票。其中展示了欧拉平面图公式 . 考虑到俄国持续的**，欧拉在1741年6月19日离开了圣彼得堡，到柏林科学院就职，职位由腓特烈二世提供。他在柏林生活了25年，并写下了不止380篇文章。在柏林，他出版了他最有名的两部作品：关于函数方面的文章《无穷小分析引论》，出版于1748年；另一部是关于微分的《微积分概论》， 出版于1755年。 在1755年，他成为瑞典皇家科学院的外籍成员。 视力恶化 在欧拉的数学生涯中，他的视力一直在恶化。在1735年一次几乎致命的发热后的三年，他的右眼近乎失明，但他把这归咎于他为圣彼得堡科学院进行的辛苦的地图学工作。视力在他在德国期间也持续恶化，以至于弗雷德里克把他誉为“独眼巨人”。欧拉的原本正常的左眼后来又遭受了白内障的困扰。在他于1766年被查出有白内障的几个星期后，导致了他的近乎完全失明。即便如此，病痛似乎并未影响到欧拉的学术生产力，这大概归因于他的心算能力和超群的记忆力。比如，欧拉可以从头到尾不犹豫地背诵维吉尔的史诗《埃涅阿斯纪》，并能指出他所背诵的那个版本的每一页的第一行和最后一行是什幺。在书记员的帮助下，欧拉在多个领域的研究其实变得更加高产了。在1775年，他平均每周就完成一篇数学论文。 其他 莱昂哈德·欧拉 欧拉**时曾研读神学，他一生虔诚、笃信上帝，并不能容许任何诋毁上帝的言论在他面前发表。有一个广泛流传的传说说到，欧拉在叶卡捷琳娜二世的宫廷里，挑战当时造访宫廷的无神论者德尼·狄德罗：“先生，，所以上帝存在，请回答！”不懂数学的德尼完全不知怎么应对，只好投降。但是由于狄德罗事实上也是一位有作为的数学家，这个传说有可能属于虚构。 欧拉是史上发表论文数第二多的数学家，全集共计75卷；他的纪录一直到了20世纪才被保罗·埃尔德什打破。后者发表的论文达1525篇，著作有32部。欧拉在他的时代，产量之多，无人能及。欧拉实际上支配了18世纪至现在的数学；对于当时新数学分支微积分，他推导出了很多结果。很多数学的分枝，也是由欧拉所创或因而有了极大的进展。 在1765年至1771年据说是因欧拉双眼直接观察太阳，双眼先后失明。尽管人生最后7年，欧拉的双目完全失明，他还是以惊人的速度产出了生平一半的著作。 1783年9月18日，晚餐后，欧拉一边喝着茶，一边和小孙女玩耍，突然之间，烟斗从他手中掉了下来。他说了一声：“我的烟斗”，并弯腰去捡，结果再也没有站起来，他抱着头说了一句：“我死了”。「欧拉停止了计算和生命」。后面这句经常被数学史家引用的话，出自法国哲学家兼数学家孔多塞之口：「...il cessa de calculer et de vivre」（he ceased to calculate and to live）。

成就

欧拉的数学符号引进和推广，并通过他的许多教科书广为流传。最为著名的，是他引进了“函数”的概念，并且第一个将函数的写为f(x)，以表示一个以x为自变量的函数。他还介绍了三角函数现代符号，为自然对数的底（现在也称为欧拉数），对求和希腊字母Σ和字母i字母E来表示虚数单位。(该使用希腊字母π来表示一个圆的周长和直径之比也由欧拉普及，但它并不是由他发明。) 欧拉创建了弹性体的力矩定律：作用在弹性细长杆上的力矩正比于物质的弹性和通过质心轴和垂直于两者的截面的转动惯量。 他还直接从牛顿运动定律出发，创建了流体力学里的欧拉方程。这些方程组在形式上等价于粘度为0的纳维-斯托克斯方程。人们对这些方程的主要兴趣在于它们能被用来研究冲击波。 他对微分方程理论作出了重要贡献。他还是欧拉近似法的创始人，这些计算法被用于计算力学中。此中最有名的被称为欧拉方法。 在数论里他引入了欧拉函数。自然数的欧拉函数被定义为小于并且与互质的自然数的个数。例如，，因为有四个自然数1，3，5和7与8互质。 在计算机领域中广泛使用的RSA公钥密码算法也正是以欧拉函数为基础的。 在分析领域，是欧拉综合了莱布尼兹的微分与牛顿的流数。 他在1735年由于解决了长期悬而未决的贝塞尔问题而获得名声： 其中是黎曼函数。 欧拉将虚数的幂定义为如下公式 这就是欧拉公式，它成为指数函数的中心。在初等分析中，从本质上来说，要幺是指数函数的变种，要幺是多项式，两者必居其一。被理乍得·费曼称为“最卓越的数学公式”的则是欧拉公式的一个简单推论（通常被称为欧拉恒等式）： 或 他在1735年定义了微分方程中的欧拉-马斯刻若尼常数，也是欧拉-麦克劳林求和公式的发现者之一，这一公式在计算难于计算的积分、求和与级数的时候极为有效： 欧拉还发现了公式的 V - e + f = 2 的数量与顶点(Vertex, V)，边(edge, e)和面(face, f)的凸多面体，因此，对一个平面图形。此公式中的常数是现在被称为欧拉示性数的图形（或其他数学对象），是有关属的对象。研究和推广这一公式，特别是通过柯西和欧莱雅Huillier，是在原点的拓扑结构。 欧拉在1736年解决了柯尼斯堡七桥问题，并且发表了论文《关于位置几何问题的解法》（Solutio problematis ad geometriam situs pertinentis），对一笔画问题进行了阐述，是最早运用图论和拓扑学的典范。 在1739年，欧拉写下了《音乐新理论的尝试（Tentamen novae theoriae musicae）》，书中试图把数学和音乐结合起来。一位传记作家写道：这是一部“为精通数学的音乐家和精通音乐的数学家而写的”著作。 在经济学方面，欧拉证明，如果产品的每个要素正好用于支付它自身的边际产量，在固定规模报酬的情形下，总收入和产出将完全耗尽。 在几何学和代数拓扑学方面，欧拉公式给出了单连通多面体的边、顶点和面之间存在的关系： 其中，F为给定多面体的面数之和，E为边数之和，V为顶点数之和。这个定理也可用于平面图。对非平面图，欧拉公式可以推广为：如果一个图可以被嵌入一个流形，则： 欧拉之墓 其中χ为此流形的欧拉示性数，在流形的连续变形下是不变量。单连通流形（例如球面或平面）的欧拉特征值是2。对任意的平面图，欧拉公式可以推广为：，其中为图中连通分支数。 数独是欧拉发明的拉丁方的概念，在当时并不流行，直到20世纪由平凡日本上班族锻治真起带起流行。

《欧拉全集》

纪念

欧拉是第六系列瑞士10法郎的钞票以及德国、俄罗斯邮票的主角。在2002年，小行星2002被命名为欧拉。基督教新教-路德教派将圣徒日历上五月二十四日定为纪念欧拉的日子。欧拉是一位虔诚的基督教徒，相信圣经是正确而没有错误的，并且极力地反对那些拥有无神论思想的人们。 日内瓦大学在智利拉西拉天文台创建的口径1.2米望远镜命名为莱昂哈德·欧拉望远镜。 2013年4月15日Google以doodle纪念欧拉306周年诞辰，展示了欧拉角、欧拉公式、欧拉恒等式、欧拉示性数和七桥问题等。

引述评价

“读欧拉的原着吧：在任何意义上，他都是我们的大师。”—拉普拉斯