Un chiffre est un signe, ou symbole, auquel est associée une valeur numérique et dont la fonction est de représenter les nombres ou écrire un numéro. Par extension de sens, le mot « chiffre » est aussi communément utilisé, au singulier comme au pluriel, avec le sens de « nombre ». D'autre part, en dehors du sens numérique ou mathématique, le chiffre est un arrangement de deux ou de plusieurs lettres initiales de noms, entrelacées l'une dans l'autre.
Étymologie
Le mot « chiffre » (chiffre, Philippe de Commynes, 1486), qui a probablement subi l'influence du picard pour la modification de la consonne initiale, provient de l'ancien français cifre (cifre, Gauthier de Coincy, 1220), d'après l'italien cifra, issu du latin médiéval cifra, lui-même emprunté à l'arabe sifr (الصِّفْر ʾaṣ-ṣifr), utilisé pour « zéro » et signifiant « le vide », le « rien », terme formé sur le modèle du sanskrit sunya, signifiant « vide ».
Synonymie partielle entre « chiffre » et « nombre »
Si les termes « chiffre » et « nombre » sont parfois confondus, ils ne sont cependant pas équivalents. À titre de comparaison, les chiffres jouent le même rôle par rapport aux nombres que les lettres par rapport aux mots. À l'écrit, les nombres sont représentés par une juxtaposition de chiffres, de même que les mots sont représentés par une juxtaposition de lettres. Ainsi, 13 (treize) est un nombre qui, en base 10, s'écrit avec les chiffres « 1 » et « 3 ». Mais, de même qu'un mot peut être constitué d'une seule lettre, tel le mot « a » (verbe « avoir » conjugué à la troisième personne du singulier au présent de l'indicatif), un chiffre seul peut représenter un nombre. Par exemple, en base 10 toujours, le nombre 4 (quatre) s'écrit avec uniquement le chiffre « 4 ».
Toutefois, dans un contexte non spécifiquement mathématique, le mot « chiffre » est utilisé dans de nombreuses expressions avec le sens de « nombre ». Par exemple, le Dictionnaire de l'Académie française indique comme seconde définition de « chiffre » : « Le nombre que figurent les chiffres ; le montant total. Le chiffre de la population d'un pays, le nombre de ses habitants. COMMERCE. Chiffre d'affaires, montant des recettes d'un exercice annuel. ». En effet, en démographie, on parle, des « chiffres de la population » et non des « nombres de la population » (voir Chiffres de population française, Chiffres de population de la France, etc.) ; et, en économie, de « chiffre d'affaires », et non de « nombre d'affaires ». Le mot « chiffre » est également parfois utilisé dans le langage courant pour désigner une proportion.
Signes et mode d'utilisation
Un nombre s'écrit comme une séquence de chiffres qui peut être de différentes longueurs. Le système unaire n'utilise qu'un seul chiffre, en forme de simple bâton et représentant la valeur 1, qui peut être répété indéfiniment pour exprimer tous les entiers naturels de façon additive. Mais il existe de nombreux systèmes de numération plus élaborés, mettant en jeu des chiffres représentant différentes valeurs. Les chiffres mis à contribution varient selon les cultures. En voici quelques exemples.
| Valeur |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
10 000 |
100 000 |
1 000 000 |
| Hiéroglyphes égyptiens |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ou |
|
| Chiffres romains |
|
Ⅰ |
|
|
|
Ⅴ |
|
|
|
|
Ⅹ |
|
|
|
Ⅼ |
|
|
|
|
Ⅽ |
|
|
|
Ⅾ |
|
|
|
|
Ⅿ |
|
|
|
| Chiffres hébreux |
|
א |
ב |
ג |
ד |
ה |
ו |
ז |
ח |
ט |
י |
כ |
ל |
מ |
נ |
ס |
ע |
פ |
צ |
ק |
ר |
ש |
ת |
ת״ק ou ך |
ת״ר ou ם |
ת״ש ou ן |
ת״ת ou ף |
תת״ק ou ץ |
|
|
|
|
| Sinogrammes |
〇 |
一 |
二 |
三 |
四 |
五 |
六 |
七 |
八 |
九 |
十 |
|
|
|
|
|
|
|
|
百 |
|
|
|
|
|
|
|
|
千 |
万 |
|
|
| Chiffres dits « arabes » |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ainsi que le montrent ces exemples, tous les systèmes de numération ne disposent pas d'un chiffre zéro. Par conséquent, ils ne permettent pas tous de représenter le nombre nul.
Par ailleurs, dans certaines écritures, il existe, en plus de ceux représentant des valeurs entières, des chiffres représentant des fractions de l'unité. Ainsi, il existe un signe tibétain pour la demi-unité, et des chiffres peuvent exprimer diverses fractions de l'unité dans de nombreuses cultures indiennes.
Le nombre de chiffres d'une numération est étroitement lié au système de numération, c'est-à-dire au mode d'utilisation de ces chiffres. Pour les systèmes additifs et hybrides, la limite du nombre de chiffres disponibles rend les nombres difficiles à représenter au-delà d'une certaines borne. Seuls les systèmes positionnels permettent de représenter aisément tous les nombres à l'aide d'un nombre limité de chiffres.
Systèmes additifs
Les systèmes additifs nécessitent, pour une base β, des chiffres pour représentant les puissances successives de β. C'est la somme de la valeur de chacun des chiffres détermine la valeur du nombre. La numération égyptienne, décimale, a ainsi des chiffres de valeur 1, 10, 100, 1000, 10 000, 100 000, 1 000 000.
Pour éviter les succession trop importantes, des chiffres de valeur intermédiaire sont parfois utilisés. C'est le cas pour la numération romaine, qui utilise des chiffres de valeur 1, 5, 10, 50, 100, 500, 1000. Cette dernière connait aussi une variante additive et soustractive, introduisant ainsi une notion d'ordre nécessaire pour interpréter la valeur d‘un nombre selon la position de ses chiffres, en leur conférant une valeur soit positive soit négative, en fonction de la comparaison de leur taille avec celle des chiffres suivants (sans que cela permette pour autant d'exprimer les nombres négatifs ou nuls).
Les numérations alphabétiques, quant à elles, utilisent des chiffres pour les différents multiples des puissances de β. Ainsi, la numération hébraïque, par exemple, utilise des chiffres pour les unités (1, 2, 3, ..., 9), dizaines (10, 20, 30, ..., 90) et centaines (100, 200, 300, ..., 900). La numération alphabétique grecque utilise des chiffres pour les mêmes valeurs, et poursuit avec les milliers (1000, 2000, 3000, ..., 9000).
Systèmes hybrides
Les systèmes hybrides nécessitent, pour une base β, des chiffres allant de 1 à β-1, plus des chiffres pour représenter les puissances successives β. Ces systèmes sont multiplicatifs et additifs : chaque chiffre utilisé représentant une puissances de β est, au besoin, précédé d'un chiffre représentant une unité (à partir de 2). La valeur du nombre est alors égal à la somme des nombres et produits de nombres en présence.
Systèmes positionnels
Les systèmes positionnels utilisent, en principe, β chiffres, de 0 à β-1, pour une base β. Le nombre de chiffres peut néanmoins être plus réduit.
Certaines numérations se passent du chiffre 0. Un simple espace palie alors à l'absence de zéro positionnel. Cela engendre toutefois des risques de mauvaises interprétations du nombre, en particulier pour les nombres se terminant par cet espace ou pour ceux nécessitant plusieurs espaces contigus.
Une base auxiliaire peut être utilisée. C'est le cas de la numération mésopotamienne, sexagésimale, qui utilise une base auxiliaire décimale. Cette numération utilise ainsi des chiffres pour les unités et pour les dizaines.
Comme le suggère la dénomination, dans un système de numération positionnel, une combinaison de chiffres représente un nombre différent selon la position qu'occupent ces chiffres. Dans une séquence de chiffres, les positions successives ont une valeur égale aux puissances successives de la base. La valeur totale d'un nombre est calculée en multipliant chacun des chiffres par la valeur de sa position, et en additionnant les résultats.
Par exemple, dans la séquence 153, le chiffre 3 occupe la première position qui, quelle que soit la base β, a pour valeur β=1. Le chiffre 5 occupe la deuxième position, qui a pour valeur β = β. Et le chiffre 1 occupe la troisième position, qui a pour valeur β.
Dans le cas d'une base dix, 153 vaut :
-
(3 × 10) + (5 × 10) + (1 × 10)
-
= (3 × 1) + (5 × 10) + (1 × 100)
-
= 3 + 50 + 100 = 153.
Enfin, pour des raisons de lisibilité, les chiffres peuvent être séparés par petits groupes au-delà d'un certain seuil. Le système de numération indo-arabe fait souvent intervenir, selon ce principe, un séparateur de positions. Le symbole utilisé pour cela est purement conventionnel ; la convention, et donc le symbole employé, varie d'ailleurs selon les pays.
Histoire
Des origines au Moyen-Âge
Le plus ancien système de numération de l'humanité est le système unaire, qui n'utilise qu'un seul chiffre, en forme de bâton, se répétant autant de fois que nécessaire pour représenter un nombre. Ce système a notamment donné naissance à de nombreux systèmes additifs, certains groupes de chiffres ayant été remplacés par de nouveaux signes afin rendre les nombres plus lisibles. Aussi, divers systèmes additifs ont été utilisés au cours de l'Antiquité, comme celui de la numération romaine. Avec les conquêtes romaines, les chiffres romains se sont alors répandus dans une large partie de l'Europe. Ils étaient ensuite communs au Moyen Âge, et leur usage perdure aujourd'hui, puisqu'ils sont couramment employés pour noter les siècles, pour la numérotation des titres de sections des textes, ou pour représenter les heures en horlogerie ou sur les cadrans solaires.
Les chiffres indo-arabes
Les chiffres arabes font partie des écritures de type logographique. C'est-à-dire que le symbole « 1 » se prononce de façon différente dans chaque langue, mais représente le même élément abstrait et reste donc compréhensible sous sa forme écrite.
Ces chiffres doivent leur nom au fait qu'ils proviennent des Arabes. L'ouvrage d'Al-Khawarizmi Traité du système de numération des Indiens (rendu accessible aux lettrés non-arabisants par ses traductions en latin, dont De numero indorum) laisse penser qu'ils seraient originaires d'Inde. Le zéro (représenté par un point) était utilisé comme marqueur de position vide par les astronomes babyloniens, mais ceux-ci n'avaient pas fait la démarche de le considérer comme chiffre à part entière.
Le concept du zéro, en tant que symbole numérique à parité avec les autres, qu'élément neutre de l'addition et élément absorbant de la multiplication, est en revanche présent dans les textes mathématiques indiens, en particulier l'analyse du problème de l'échiquier et des grains de blé.
Les chiffres de 1 à 9 ont été inventés en Inde. Ils apparaissent dans des inscriptions de Nana Ghât au III siècle av. J.-C. La numération de position avec un zéro (un simple point à l'origine), a été développée au cours du V siècle. Dans un traité de cosmologie en sanskrit de 458, on voit apparaître le nombre 14 236 713 écrit en toutes lettres. On y trouve aussi le mot « sunya » (le vide), qui représente le zéro. C'est à ce jour le document le plus ancien faisant référence à cette numération.
Au X siècle, le moine occitan Gerbert d'Aurillac s'initie à la nouvelle numération et, grâce aux chaires qu'il occupe dans divers établissements religieux d'Europe, commence à le faire connaître aux lettrés d'Occident. Élu pape en 999 sous le nom de Sylvestre II, il en retire l'autorité nécessaire pour faire adopter à la chrétienté la numération indo-arabe malgré la réticence du milieu des clercs, utilisant pour leur part l'abaque, et qui voient cette simplification menacer une partie de leur métier.
Les dix chiffres indiens ont été adoptés dans le monde arabo-musulman, puis dans le monde chrétien. De nos jours, on écrit ces chiffres ainsi
Au Moyen-Orient : ٠, ١, ٢, ٣, ٤, ٥, ٦, ٧, ٨ et ٩.
Au Maghreb et en Occident : 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9.
Mathématiques
En mathématiques, on utilise ordinairement les chiffres arabes, dont l'appellation est ambigüe puisque leur tracé a connu des évolutions en Europe après leur emprunt aux Arabes, et que les Arabes disposent de chiffres qui diffèrent de ceux-là.
Ces dix chiffres sont ceux du système décimal employé par défaut : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Le nombre de chiffres utilisés dépend de la base. En effet, n chiffres sont nécessaires pour représenter tous les entiers dans une base n fixe.
Si n est inférieur à 10, on utilise généralement les n premiers chiffres, à partir de 0. Par exemple, dans le système binaire, on n'emploie que deux chiffres : 0 et 1. Ce système est souvent utilisé pour représenter des valeurs telles que « vrai » et « faux », « marche » et « arrêt ». Il convient notamment pour représenter le fonctionnement de l'électronique numérique utilisée dans les ordinateurs, d'où son usage en informatique et en électronique.
Si n est strictement supérieur à 10 et inférieur à 36, on utilise les chiffres de 0 à 9, et, par convention, on poursuit avec (n−10) lettres de l'alphabet latin à partir de A. Ainsi, les chiffres du système hexadécimal sont 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, leur valeur allant, dans l'ordre, de 0 à 15. Ce système est surtout utilisé en informatique.
Si n est strictement supérieur à 36, on utilise une base dix auxiliaire : les chiffres sont représentés par un nombre en base 10, et sont dissociés les uns des autres par un séparateur de position.
Généralement, le signe des nombres n'est pas indiqué par les chiffres eux-mêmes, mais par l'adjonction d'un signe supplémentaire, soit +, soit −. Cependant, les chiffres exprimant une valeur positive, le nombre représenté, sans indication supplémentaire de signe, est également positif. De ce fait, le signe + est rarement employé.
Cependant, il existe aussi des systèmes balancés, employant des chiffres signés. Par exemple, le système trinaire balancé utilise les chiffres 1, 0, 1, valant, respectivement, -1, 0, 1. Il est adapté pour représenter les booléens dont les valeurs sont « vrai », « faux » et « indéterminé », et est pratique pour l'informatique, car il évite l'ajout d'un chiffre supplémentaire pour indiquer le signe d'un nombre. Dans un tel système, les nombres positifs et négatifs bénéficient de la même représentation.
Un système de numération n'implique pas nécessairement l'utilisation du chiffre zéro. La numération bijective en base k permet notamment de représenter tous les entiers sans faire appel à ce dernier.
Il existe aussi des systèmes pour lesquels certains nombres peuvent être représentés par plusieurs séquences de chiffres différentes. Dans le système de numération d'Avizienis, par exemple, tous les nombres n'ont pas une représentation unique.
D'autre part, des chiffres supplémentaires sont aussi utilisés pour exprimer des nombres de certains ensembles de nombres. Par exemple, pour noter les nombres complexes, un chiffre est représenté par la lettre i (chiffre dit « imaginaire », parfois noté j dans les formules utilisées dans d'autres sciences comme l'électricité, l'électromagnétisme et le traitement du signal) et s'emploie comme une quantité multiplicative, combinable par des opérations arithmétiques simples pour exprimer le nombre complexe quelconque. Dans d'autre cas, on lui préfère une notation algébrique sous forme de couple (aussi utilisée pour noter les coordonnées).
Enfin, il existe des représentations des nombres pour lesquelles le nombre de chiffres nécessaires n'est pas limité. C'est le cas, par exemple de la suite des exposants dans la décomposition d'un nombre entier sous forme de produit de puissances de nombre premiers : il est alors nécessaire d'utiliser un séparateur entre les chiffres qui eux-mêmes sont des nombres entiers qui sont exprimés sous forme positionnelle dans une base fixe.

 词典释义:
词典释义:
 字
字 字
字
 学, 算术
学, 算术 目, 总
目, 总 , 总额
, 总额

 政策
政策 ]
] 
 码;译电处
码;译电处 码写
码写 )
) 码
码 字, 字母组合
字, 字母组合
 码
码 图案
图案 家用布巾
家用布巾 字
字 增长
增长 ;
;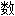 目,
目,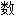 量
量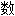 ;
;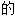 ,升高
,升高 ,上行
,上行 ;
; ,预测
,预测 ;
;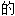 ,年度
,年度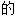 ;
;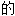 ,有含义
,有含义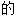 ,意味深长
,意味深长 ;
; ,
,  字;
字;  额;
额;  码
码
 字
字 额
额 字
字 字
字