En analyse, le nombre dérivé en un « point » (réel) x d'une fonction f à variable et valeurs réelles est le coefficient directeur de la tangente au graphe de f au point (x, f(x)). C'est le coefficient directeur de l'approximation affine de f en x ; ce nombre n'est donc défini que si cette tangente — ou cette approximation — existe.

La dérivée d'une fonction f est une fonction qui, à tout nombre pour lequel f admet un nombre dérivé, associe ce nombre dérivé. La dérivée en un point d'une fonction de plusieurs variables réelles, ou à valeurs vectorielles (en), est plus couramment appelée différentielle de la fonction en ce point, et n'est pas traitée ici.

La notion de nombre dérivé a vu le jour au XVII siècle dans les écrits de Leibniz et de Newton qui le nomme fluxion et qui le définit comme « le quotient ultime de deux accroissements évanescents ».

La dérivée de la fonction f {\displaystyle f\,} est notée en mathématiques f ′ {\displaystyle f'\,} ou d f d x {\displaystyle {\frac {{\mathrm {d} }f}{{\mathrm {d} }x}}} . On utilise aussi des notations spécifiques (surtout en physique) pour désigner la dérivée par rapport au temps qui s'écrit avec un point surmontant la lettre ( f ˙ {\displaystyle {\dot {f}}} ), la dérivée seconde s'écrivant alors grâce à un tréma surmontant la lettre. Cette notation est appelée « notation de Newton ». On utilise dans le même esprit, les notations prime et seconde pour noter la dérivée par rapport à l'espace.

La notion de dérivée est une notion fondamentale en analyse. Elle permet d'étudier les variations d'une fonction, de construire des tangentes à une courbe et de résoudre des problèmes d'optimisation.

En sciences, lorsqu'une grandeur est fonction du temps, la dérivée de cette grandeur donne la vitesse instantanée de variation de cette grandeur, et la dérivée de la dérivée donne l'accélération. Par exemple, la vitesse instantanée d'un mobile est la valeur à cet instant de la dérivée de sa position par rapport au temps, et son accélération est la valeur à cet instant de la dérivée par rapport au temps, de sa vitesse.

On généralise la notion de dérivée en étendant celle-ci au champ complexe et on parle alors de dérivée complexe. Pour une fonction de plusieurs variables réelles, on parle de la dérivée partielle par rapport à l'une de ses variables.

Il existe aussi une définition purement algébrique de la dérivée. On en trouve un exemple dans l'article polynôme formel.

Approche intuitive

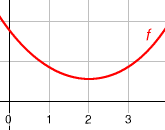
En 0, la courbe est décroissante, donc le coefficient directeur de la tangente à la courbe en ce point est négatif, et donc, le nombre dérivé y est négatif (il vaut -1). En 1, la courbe est toujours décroissante, mais la pente y est moindre (-0,5). En 2, la courbe est parfaitement horizontale, donc la dérivée est nulle (0). En 3, la courbe est croissante, donc le nombre dérivé y est positif (0,5).

Pour approcher cette notion de manière intuitive, commençons par nous donner une courbe représentative d'une fonction continue dans un repère cartésien, c'est-à-dire tracée d'un seul trait de crayon, et bien « lisse » ; on dira là que la fonction associée est dérivable.

Quel que soit le point que l'on choisit sur la courbe, on pourra alors tracer ce qu'on appelle une tangente, c'est-à-dire une droite qui épouse localement la direction de cette courbe. Si l'on trace la courbe et sa tangente et que l'on s'approche en zoomant suffisamment, on aura de plus en plus de mal à distinguer la courbe de sa tangente. Si la courbe « monte » (c'est-à-dire si la fonction associée est croissante), la tangente sera également montante ; inversement, si la fonction est décroissante, la tangente sera descendante.

Si on se donne une abscisse x 0 {\displaystyle x_{0}} pour laquelle la fonction f {\displaystyle f\,} est dérivable, on appelle nombre dérivé de f {\displaystyle f\,} en x 0 {\displaystyle x_{0}} le coefficient directeur de la tangente à la courbe au point d'abscisse x 0 {\displaystyle x_{0}} . Ce réel donne de précieuses informations sur le comportement local d'une fonction : c'est la mesure algébrique de la vitesse à laquelle cette fonction change lorsque sa variable change.

Ainsi, si le nombre dérivé d'une fonction est positif sur un intervalle, cette fonction sera croissante sur ce même intervalle. Inversement, s'il est négatif, elle sera décroissante. Lorsque le nombre dérivé est nul en un point, la courbe admet une tangente horizontale en ce point (pour plus de détails, voir Fonction monotone#Monotonie et signe de la dérivée).

Approche historique

Gottfried Wilhelm von Leibniz

Dès la seconde moitié du XVII siècle, le domaine mathématique de l'analyse numérique connut une avancée prodigieuse grâce aux travaux de Newton et de Leibniz en matière de calcul différentiel et intégral, traitant notamment de la notion d'infiniment petit et de son rapport avec les sommes dites intégrales.

C'est cependant Blaise Pascal qui, dans la première moitié du XVII siècle, a le premier mené des études sur la notion de tangente à une courbe - lui-même les appelait « touchantes ». Le marquis de l'Hospital contribuera à diffuser le calcul différentiel de Leibniz à la fin du XVII siècle grâce à son livre sur l'analyse des infiniment petits. Wallis, mathématicien anglais (surtout connu pour la suite d'intégrales qui porte son nom) contribua également à l'essor de l'analyse différentielle.

Jean Le Rond d'Alembert.

Néanmoins cette théorie tout juste éclose n'est pas encore, à l'époque, pourvue de toute la rigueur mathématique qu'elle aurait exigée, et notamment la notion d'infiniment petit introduite par Newton, qui tient plus de l'intuitif, et qui pourrait engendrer des erreurs dès lors que l'on ne s'entend pas bien sur ce qui est ou non négligeable. C'est au XVIII siècle que d'Alembert introduit la définition plus rigoureuse du nombre dérivé en tant que limite du taux d'accroissement - sous une forme semblable à celle qui est utilisée et enseignée de nos jours. Cependant, à l'époque de d'Alembert, c'est la notion de limite qui pose problème : R {\displaystyle \mathbb {R} } n'est pas encore construit formellement (voir Construction des nombres réels). C'est seulement avec les travaux de Weierstrass au milieu du XIX siècle que le concept de dérivée sera entièrement formalisé.

C'est à Lagrange (fin du XVIII siècle) que l'on doit la notation f ′ ( x ) {\displaystyle f'(x)} , aujourd'hui usuelle, pour désigner le nombre dérivé de f {\displaystyle f} en x {\displaystyle x} . C'est aussi à lui qu'on doit le nom de « dérivée » pour désigner ce concept mathématique.

Définition formelle

Soit f {\displaystyle f\,} une fonction réelle à valeurs réelles définie sur une réunion quelconque d'intervalles non triviaux, et x 0 {\displaystyle x\,_{0}} appartenant à l'intérieur de l'ensemble de définition D f {\displaystyle {\mathcal {D}}_{f}} .

Pour tout ${\displaystyle h\in \mathbb {R} ^{*}}$ tel que ${\displaystyle [x_{0},x_{0}+h]\subset {\mathcal {D}}_{f}}$, on appelle taux d'accroissement de ${\displaystyle f\,}$ en ${\displaystyle x\,_{0}}$ et avec un pas de ${\displaystyle h\,}$ la quantité :

${\displaystyle t_{x_{0}}(h)={f(x_{0}+h)-f(x_{0}) \over h}}$

Il s'agit du coefficient directeur de la droite reliant les points de coordonnées ( x 0 , f ( x 0 ) ) {\displaystyle (x_{0},f(x_{0}))} et ( x 0 + h , f ( x 0 + h ) ) {\displaystyle (x_{0}+h,f(x_{0}+h))} . Si t x 0 ( h ) {\displaystyle t_{x_{0}}(h)} admet une limite finie lorsque h {\displaystyle h\,} tend vers 0, on dit que f {\displaystyle f} est dérivable en x 0 {\displaystyle x_{0}} , auquel cas le nombre dérivé de f {\displaystyle f\,} en x 0 {\displaystyle x_{0}} est égal à la limite de ce taux d'accroissement. On note alors :

${\displaystyle f'(x_{0})=\lim _{h\to 0 \atop h\neq 0}t_{x_{0}}(h)=\lim _{h\to 0 \atop h\neq 0}{f(x_{0}+h)-f(x_{0}) \over h}}$

Ou, de manière équivalente :

${\displaystyle f'(x_{0})=\lim _{x\to x_{0} \atop x\neq x_{0}}{f(x)-f(x_{0}) \over x-x_{0}}}$

Une fonction pour laquelle le taux d'accroissement en un point admet une limite finie (qui est le nombre dérivé) est dite dérivable en ce point.

Ce calcul de limite revient graphiquement à rechercher la pente de la tangente à la courbe en ce point. Ainsi, le nombre dérivé d'une fonction en un point, s'il existe, est égal à la pente de la tangente à la courbe représentative de la fonction en ce point.

La dérivation peut aussi être définie pour des fonctions d'une variable réelle à valeurs dans d'autres ensembles que ${\displaystyle \mathbb {R} }$.

Par exemple, une fonction f {\displaystyle f\,} d'une variable réelle, à valeurs dans R n {\displaystyle \mathbb {R} ^{n}} , est dérivable en x 0 {\displaystyle x\,_{0}} si et seulement si toutes ses coordonnées sont dérivables en x 0 {\displaystyle x\,_{0}} ; et sa dérivée est la fonction dont les coordonnées sont les dérivées des coordonnées de f {\displaystyle f\,} . C'est un cas particulier de fonctions de variable vectorielle et à valeur dans un espace vectoriel normé ou métrique.

Dérivabilité et lien avec la continuité

Typiquement, une fonction est dérivable si elle ne présente pas « d'aspérité », de rupture de pente ni de partie « verticale ».

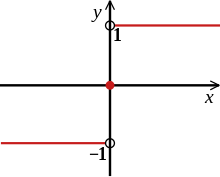
Fonction signe.

Une fonction qui n'est pas continue en un point n'y est pas dérivable : comme la fonction fait un saut, on ne peut pas définir de tangente, la limite du taux de variation est infini (la pente de la courbe est verticale). C'est le cas par exemple de la fonction signe sgn(x) en 0 :

à gauche de 0 (-∞ < x < 0), sgn(x) = -1 ;

en 0 : sgn(0) = 0 ;

à droite de 0 (0 < x < +∞), sgn(x) = +1 ;

le taux de variation pour une largeur h vaut donc

(1 - (-1))/h

et tend vers +∞ quand h tend vers 0. Par contre, on peut définir une dérivée à gauche — dérivée partout nulle (tangente horizontale) sur ]-∞ ; 0[ — et une dérivée à droite — dérivée également nulle sur ]0 ; +∞[.

Fonction valeur absolue.

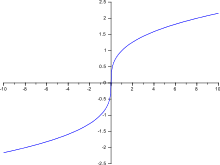
Fonction racine cubique.

Si une fonction est dérivable en un point alors elle est continue en ce point, mais la réciproque est fausse.

Par exemple : la fonction ${\displaystyle x\mapsto |x|}$ est continue mais n'est pas dérivable en 0 :

à gauche, la pente vaut -1 ;

à droite, la pente vaut +1 ;

il y a une tangente à gauche et une tangente à droite différentes, la pente en 0 n'est pas définie ; le taux de variation n'a pas de limite définie. C'est le cas général pour les courbes présentant un point anguleux.

Il en est de même de la fonction racine cubique, qui a une tangente verticale en x = 0 : le taux de variation a une limite infinie.

Fonction dérivée

La dérivabilité est a priori une notion locale (dérivabilité en un point), mais si une fonction est dérivable en tout point d'un intervalle, on peut définir sa fonction dérivée sur l'intervalle en question. La fonction dérivée de f {\displaystyle f} , souvent notée f ′ {\displaystyle f'\,} (prononcer « f {\displaystyle f} prime ») est définie sur D f {\displaystyle {\mathfrak {D}}_{f}} et le domaine de dérivabilité de f {\displaystyle f} (ensemble des points de R {\displaystyle \mathbb {R} } en lesquels f {\displaystyle f} est dérivable) est défini par :

${\displaystyle f'\colon {\mathfrak {D}}_{f}\rightarrow \mathbb {R} ,\quad x\mapsto f'(x)}$

C'est la fonction qui prend en tout point de ${\displaystyle {\mathfrak {D}}_{f}}$ la valeur du nombre dérivé de ${\displaystyle f\,}$ en ce point.

Ainsi, lorsque la fonction dérivable f {\displaystyle f} est croissante, la fonction dérivée f ′ {\displaystyle f'\,} est positive. f ′ {\displaystyle f'\,} s'annule aux points où f {\displaystyle f} admet des tangentes horizontales.

Les fonctions dérivées sont utilisées notamment dans l'étude des fonctions réelles et dans les équations différentielles. La seule fonction (à une constante multiplicative près) égale à sa dérivée est la fonction exponentielle de base e {\displaystyle e} (celle-ci est solution de y ′ = y {\displaystyle y'=y} , cf. article détaillé).

Notations

Il existe différentes notations pour exprimer la valeur de la dérivée d'une fonction ${\displaystyle f}$ en un point ${\displaystyle a}$. On distingue :

la notation de Lagrange : f ′ ( a ) {\displaystyle f'\left(a\right)} ;

la notation de Leibniz : d f d x ( a ) {\displaystyle {\frac {{\mathrm {d} }f}{{\mathrm {d} }x}}(a)} ou d f d x | x = a {\displaystyle \left.{\frac {{\mathrm {d} }f}{{\mathrm {d} }x}}\right|_{x=a}} ou même, moins rigoureusement, d ( f ( a ) ) d x {\displaystyle {\frac {{\mathrm {d} }\left(f(a)\right)}{{\mathrm {d} }x}}} ;

la notation d'Isaac Newton : f ˙ ( a ) {\displaystyle {\dot {f}}(a)} qui est plutôt utilisée en physique pour désigner une dérivée par rapport au temps (on parle alors de calcul des fluxions) ;

la notation d'Euler : D x f ( a ) {\displaystyle D_{x}f(a)} .

Dérivées usuelles et règles de dérivation

f ′ {\displaystyle f'\,} peut souvent se calculer directement à partir d'une expression de f {\displaystyle f\,} , lorsqu'il s'agit d'une fonction « simple », en utilisant la table des dérivées usuelles. Pour des fonctions qui s'expriment comme combinaison linéaire de fonctions simples, comme produit, quotient ou composée, on utilise un petit nombre de règles algébriques déduites de la définition donnée plus haut. Les règles les plus couramment utilisées sont les suivantes :

Nom Règle Conditions Linéarité ( a f ) ′ = a f ′ {\displaystyle (af)^{\prime }=af'} Quels que soient la fonction dérivable f {\displaystyle f\,} et le réel a. Linéarité ( f + g ) ′ = f ′ + g ′ {\displaystyle (f+g)^{\prime }=f'+g'} Quelles que soient les fonctions dérivables f {\displaystyle f\,} et g {\displaystyle g\,} . Produit ( f g ) ′ = f ′ g + f g ′ {\displaystyle (fg)^{\prime }=f'g+fg'} Quelles que soient les fonctions dérivables f {\displaystyle f\,} et g {\displaystyle g\,} . Inverse ( 1 g ) ′ = − g ′ g 2 {\displaystyle \left({1 \over g}\right)'={-g' \over g^{2}}} Quelle que soit la fonction dérivable g {\displaystyle g\,} qui ne s'annule pas (cas particulier f =1 de la ligne suivante) Quotient ( f g ) ′ = f ′ g − f g ′ g 2 {\displaystyle \left({f \over g}\right)'={f'g-fg' \over g^{2}}} Quelles que soient la fonction dérivable f {\displaystyle f\,} et la fonction dérivable g {\displaystyle g\,} qui ne s'annule pas Composée ( g ∘ f ) ′ = ( g ′ ∘ f ) ⋅ f ′ {\displaystyle (g\circ f)'=(g'\circ f)\cdot f'} Quelles que soient les fonctions dérivables (et composables) f {\displaystyle f\,} et g {\displaystyle g\,} Réciproque ( f − 1 ) ′ = 1 f ′ ∘ f − 1 {\displaystyle (f^{-1})'={\frac {1}{f'\circ f^{-1}}}} Quelle que soit la fonction f {\displaystyle f\,} bijective de réciproque f − 1 {\displaystyle f^{-1}\,} , dérivable de dérivée ne s'annulant en aucun point

En particulier, voici les règles courantes se déduisant de la dérivée de composées :

Nom	Règle	Conditions
Puissance	${\displaystyle (f^{\alpha })^{\prime }=\alpha f^{\alpha -1}f'}$	Quel que soit ${\displaystyle \alpha \in \mathbb {Z} }$, et même quel que soit ${\displaystyle \alpha \in \mathbb {R} }$ si f est positive
Racine	${\displaystyle \left({\sqrt {f}}\right)'={f' \over 2{\sqrt {f}}}}$	Quelle que soit la fonction dérivable ${\displaystyle f\,}$ strictement positive (cas particulier α=1/2 de la ligne précédente)
Exponentielle	${\displaystyle ({\mbox{e}}^{f})^{\prime }={\mbox{e}}^{f}\cdot f'}$	Quelle que soit ${\displaystyle f\,}$ dérivable
Logarithme	${\displaystyle (\log _{b}f)^{\prime }={f' \over f\cdot \ln b}}$	Quelle que soit la fonction dérivable ${\displaystyle f\,}$ strictement positive
Logarithme	${\displaystyle (\ln f)^{\prime }={f' \over f}}$	Quelle que soit la fonction dérivable ${\displaystyle f\,}$ strictement positive (cas b=e de la ligne précédente)

Dérivation numérique

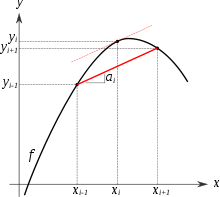
Principe de la dérivation numérique

Dans le cas d'une courbe expérimentale, on ne possède pas de fonction analytique pour la décrire, mais d'une série de valeurs (x_i , y_i ). On a donc recours à une dérivation numérique, qui consiste simplement à approcher la valeur de la dérivée en un point i calculer le taux de variation entre les points précédent et suivant :

${\displaystyle f'(x_{i})\simeq {\frac {y_{i+1y_{i-1}}{x_{i+1x_{i-1}}}}$

Graphiquement, cela revient à remplacer la tangente par la corde. Ceci peut se justifier par le théorème des accroissements finis : on sait qu'il existe un point de l'intervalle [xi-1 , xi+1] pour lequel la dérivée est la pente de la corde, et si l'intervalle est petit, alors ce point est proche du milieu xi . Cette méthode est automatisable sur les calculatrices programmables et les ordinateurs.

Là, Il faut se poser la question de la précision des résultats. Une mise en informatique « naïve » de la méthode de calcul peut mener à des résultats de précision médiocre dans certains cas.

Dans un ordinateur, la précision des nombres est limitée par le mode de représentation. Si l'on utilise la double précision selon la norme IEEE 754, les nombres ont environ 16 chiffres significatifs. On a donc une précision relative de l'ordre de 10 (en fait, 2). Notons r cette valeur : r = 10. Les calculatrices de poche admettent typiquement 10 chiffres significatifs, soit r = 10.

Supposons que la différence y_{i + 1} - y_{i - 1} soit inférieure à r, alors le calculateur fera une erreur grossière sur le calcul et le résultat sera médiocre ; voire, si la différence est très faible, il ne « verra pas » de différence entre les deux valeurs, et le résultat sera 0. Si par exemple on veut avoir la dérivée autour de 2 de la fonction ƒ(x) = x, en prenant un écart de 10 entre les points :

x₁ = 1,999 999 999 999 9 ; x₂ = 2 ; x₃ = 2,000 000 000 000 1

δ = y₃ - y₁ = x₃ - x₁ ≈ 8·10

On voit que la différence entre les nombres, 8·10, est proche de r. On va donc avoir une erreur d'arrondi. De fait, le calcul nous donne sur un ordinateur

ƒ'(2) ≈ 3,997

alors que le résultat exact est

ƒ'(2) = 2×2 = 4

soit une erreur de 0,3 %. Sur une calculatrice, le résultat est ƒ'(2) ≈ 0…

Le point critique est le choix de l'écart h entre les valeurs de x. Une valeur de l'ordre de r {\displaystyle {\sqrt {r}}} convient dans de nombreux cas. Il nous manque encore quelques éléments pour cette étude ; le problème est abordé dans la section Précision de la dérivée numérique ci-dessous.

Donc :

pour un ordinateur calculant en double précision, on peut prendre un écart de 10 entre les points ;

pour une calculatrice avec 10 chiffres significatifs, on peut prendre un écart de 10 entre les points.

Dérivation graphique

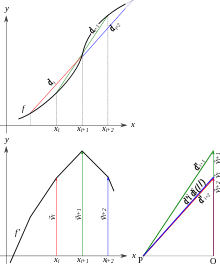
Dérivation graphique : on convertit la pente des droites en utilisant un pôle

On peut également effectuer une dérivation graphique, sans utiliser de calcul. On approche les tangentes par les cordes comme pour la méthode numérique. Puis, on tire des parallèles à ces droites passant par un point nommé pôle P. On considère l'intersection de ces droites avec la verticale passant par O, le segment [OP] étant horizontal. La hauteur v_i des segments ainsi délimités est proportionnelle à la pente a_i :

${\displaystyle v_{i}=\mathrm {OP} \times a_{i}}$

on peut donc reporter cette hauteur sur le graphique et obtenir une approximation de la courbe dérivée. L'échelle de l'axe des y est donc de OP:1.

Dérivée d'ordre n

La dérivée seconde, notée ƒ", est la dérivée de la dérivée de ƒ, lorsqu'elle existe :

${\displaystyle f''=(f')'}$

et la dérivée troisième est la dérivée de la dérivée seconde, lorsqu'elle existe :

${\displaystyle f'''=(f'')'}$.

De manière générale, on définit la dérivée d'ordre n {\displaystyle n} pour une fonction n {\displaystyle n} fois dérivable par récurrence :

${\displaystyle {\frac {{\mathrm {d} }^{n+1}f}{{\mathrm {d} }x^{n+1}}}={\frac {\mathrm {d} }{{\mathrm {d} }x}}{\frac {{\mathrm {d} }^{n}f}{{\mathrm {d} }x^{n}}}}$

${\displaystyle {\frac {{\mathrm {d} }^{n}f}{{\mathrm {d} }x^{n}}}}$ est également notée ${\displaystyle f^{(n)}}$.

Formule de Leibniz

Si f {\displaystyle f} et g {\displaystyle g} sont des fonctions n {\displaystyle n} fois dérivables, alors, par application de la règle du produit :

${\displaystyle (fg)^{(n)}=\sum _{k=0}^{n}{n \choose k}f^{(k)}g^{(n-k)}}$.

En particulier pour ${\displaystyle n=2}$,

${\displaystyle (fg)''=f''g+2f'g'+fg''~}$

On notera l'analogie avec la formule du binôme de Newton. Cela provient de la bilinéarité de l'opérateur dérivation.

Propriétés des fonctions dérivables

Théorème de Rolle

Soient ${\displaystyle a}$ et ${\displaystyle b}$ deux réels tels que ${\displaystyle a<b}$. Si ${\displaystyle f}$ est continue sur ${\displaystyle [a,b]}$, dérivable sur ${\displaystyle ]a,b[}$, et si ${\displaystyle f(a)=f(b)}$, alors il existe (au moins) un réel ${\displaystyle c}$ dans ${\displaystyle ]a,b[}$ tel que :

${\displaystyle f'(c)=0~}$ .

Théorème des accroissements finis

Énoncé

Si une fonction ${\displaystyle f}$ est continue sur ${\displaystyle [a,b]}$, avec ${\displaystyle a\neq b}$, et dérivable sur ${\displaystyle {]a,b[}}$, alors il existe un point ${\displaystyle x_{0}}$ de ${\displaystyle {]a,b[}}$ tel que le nombre dérivé de ${\displaystyle f}$ en ce point soit le taux de variation entre ${\displaystyle a}$ et ${\displaystyle b}$

${\displaystyle f'(x_{0})={\frac {f(b)-f(a)}{b-a}}}$

En particulier, si f ( a ) = f ( b ) {\displaystyle f(a)=f(b)} , on retrouve le théorème de Rolle, qui sert aussi à démontrer le résultat plus général (voir l'article détaillé), c'est pourquoi on le rencontre souvent sous le nom de lemme de Rolle. Cette propriété est utilisée en cinématique pour déterminer une approximation du vecteur vitesse à partir d'un relevé de point.

Théorème de Darboux

Si f est dérivable, sa fonction dérivée f' n'est pas nécessairement continue. Cependant f' possède la propriété des valeurs intermédiaires. Ceci constitue le théorème de Darboux, qui peut se formuler de deux façons équivalentes : si f dérivable est définie sur I intervalle de R, f'(I) est un intervalle, ou : si f'(a)<f'(b), pour tout t de [f'(a),f'(b)], il existe c tel que f'(c)=t.

Dérivées de fonctions liées

Beaucoup de problèmes font intervenir plusieurs variables qui sont liées entre elles et qui varient en fonction du temps. La variation de l'une de ces variables donnera une variation correspondante des autres variables. Le lien entre ces variations dépendra des relations qui existent entre les variables.

Exemple : Un homme s'éloigne d'une tour de 60 m de hauteur à raison de 8 km/h soit environ 2,2 m/s. A quelle vitesse s'éloigne t-il du sommet de cette tour lorsqu'il est à 80 m du pied de la tour? On sait par relation de Pythagore que la distance entre le piéton et le sommet est alors de 100 m. y et x, distances du piéton au sommet de la tour et au pied de celle-ci sont des fonctions du temps liées par la relation de Pythagore : y 2 = x 2 + 60 2 {\displaystyle y^{2}=x^{2}+60^{2}} implique y 2 ( t ) = x 2 ( t ) + 60 2 {\displaystyle y^{2}(t)=x^{2}(t)+60^{2}} En dérivant les 2 membres de cette égalité, nous obtenons : 2 y d y d t = 2 x d x d t {\displaystyle 2y{\frac {{\mathrm {d} }y}{{\mathrm {d} }t}}=2x{\frac {{\mathrm {d} }x}{{\mathrm {d} }t}}} implique d y d t = x y d x d t {\displaystyle {\frac {{\mathrm {d} }y}{{\mathrm {d} }t}}={\frac {x}{y}}{\frac {{\mathrm {d} }x}{{\mathrm {d} }t}}} : la vitesse par rapport au sommet de la tour vaut le rapport entre la distance au sol entre le piéton et le pied de la tour et la distance entre le piéton et le sommet de la tour multiplié par la vitesse du piéton. Lorsque le piéton est à 80 m du pied de la tour : d y d t = 80 100 d x d t = 8 10 d x d t {\displaystyle {\frac {{\mathrm {d} }y}{{\mathrm {d} }t}}={\frac {80}{100}}{\frac {{\mathrm {d} }x}{{\mathrm {d} }t}}={\frac {8}{10}}{\frac {{\mathrm {d} }x}{{\mathrm {d} }t}}} , ce qui revient à dire que la vitesse par rapport au sommet de la tour vaut 8 10 ⋅ 8 k m h = 6 , 4 k m h {\displaystyle {\tfrac {8}{10}}\cdot 8\;{\rm {{\tfrac {km}{h}}=6,{}4\;{\tfrac {km}{h}}}}} . L'expression précédente permet en outre d'exprimer en fonction du temps la vitesse mesurée du sommet de la tour : si l'on note v ( t ) {\displaystyle v(t)} celle-ci et v {\displaystyle v} la vitesse constante de déplacement horizontal exprimées en m/s, on a les égalités x ( t ) = v t {\displaystyle x(t)=vt} , y ( t ) = 60 2 + v 2 t 2 {\displaystyle y(t)={\sqrt {60^{2}+v^{2}t^{2}}}} et v ( t ) = v t 60 2 + v 2 t 2 v {\displaystyle v(t)={\frac {vt}{\sqrt {60^{2}+v^{2}t^{2}}}}v}

Analyse d'une fonction dérivée

En trouvant les valeurs de x pour lesquelles la dérivée vaut 0 ou n'existe pas, on trouve les nombres critiques de la fonction. Les nombres critiques de f permettent de trouver implicitement ses maxima et ses minima. En effectuant le test de la dérivée première, on construit un tableau de variation ; si le signe de la fonction dérivée passe du plus au moins devant un nombre critique, on a un maximum et si le signe de la fonction dérivée passe du moins au plus devant le nombre critique, on a un minimum. De plus, lorsque le signe de la dérivée première est positif, la fonction est croissante ; s'il est négatif, elle est décroissante. On ne conclut rien, si au point critique la fonction dérivée ne change pas de signe. En dérivant la dérivée première, on a la dérivée seconde. En effectuant le test de la dérivée seconde, on trouve les nombres critiques de la dérivée première pour les placer dans le même tableau ; lorsqu'on observe un changement de signe de la dérivée seconde devant ce ou ces nombres critiques, on dit qu'on a un (ou des) point(s) d'inflexion. Les points d'inflexion marquent un changement de la concavité de la fonction. Un signe positif de la dérivée seconde signifie que la fonction est convexe et un signe négatif de la dérivée seconde signifie que la fonction est concave. Connaissant les changements de concavité et les extrema de la fonction, on peut alors tracer une esquisse de sa représentation graphique.

Dérivée et optimisation

Méthode pour optimiser un rendement à l'aide du calcul différentiel:

Mathématisation Définitions et dessin : on définit les variables inconnues et on les représente sur un schéma. Écrire la fonction objectif à deux variables et préciser si on recherche un maximum ou un minimum dans la situation donnée. Trouver la relation entre les deux variables. Écrire la fonction objectif à une variable et préciser le domaine de la fonction.

Définitions et dessin : on définit les variables inconnues et on les représente sur un schéma.

Écrire la fonction objectif à deux variables et préciser si on recherche un maximum ou un minimum dans la situation donnée.

Trouver la relation entre les deux variables.

Écrire la fonction objectif à une variable et préciser le domaine de la fonction.

Analyse Dériver la fonction pour obtenir la dérivée première. Trouver les nombres critiques de la fonction, où la dérivée première vaut zéro ou n'existe pas dans les intervalles du domaine. Effectuer le test de la dérivée première ou le test de la dérivée seconde pour déterminer le maximum ou le minimum recherché de la situation.

Dériver la fonction pour obtenir la dérivée première.

Trouver les nombres critiques de la fonction, où la dérivée première vaut zéro ou n'existe pas dans les intervalles du domaine.

Effectuer le test de la dérivée première ou le test de la dérivée seconde pour déterminer le maximum ou le minimum recherché de la situation.

On formule la réponse de façon concise par rapport à la question.

Dérivée algébrique

Les algébristes donnent un sens un peu différent au terme dérivée. Ils l'appliquent à une structure B appelée A-algèbre associative unitaire et commutative. Une application D, de B dans B est appelée une dérivation si :

L'application D est A-linéaire.

b1 et b2 étant deux éléments de B, la dérivée de b1.b2 est égale à la somme du produit de la dérivée de b1 et de b2 et du produit de b1 avec la dérivée de b2 : D ( b 1 ⋅ b 2 ) = D ( b 1 ) ⋅ b 2 + b 1 ⋅ D ( b 2 ) {\displaystyle D(b_{1}\cdot b_{2})=D(b_{1})\cdot b_{2}+b_{1}\cdot D(b_{2})} (en particulier, la dérivée de l'élément 1B neutre de B pour la multiplication est nulle).

Un exemple de dérivation définie de cette manière est donné dans l'article détaillé.

Précision de la dérivée numérique

On peut approcher la fonction ƒ par un polynôme appelé développement limité :

${\displaystyle f(x+h)=f(x)+f'(x)\cdot h+{\frac {f''(x)}{2}}\cdot h^{2}+\mathrm {O} (h^{2})}$

il en vient une approximation de la dérivée :

${\displaystyle f'(x)\simeq {\frac {f(x+h)-f(x)}{h}}\frac {f''(x)}{2}}\cdot h\simeq {\frac {f(x+h)-f(x)}{h}}}$

Ce faisant, on commet une erreur de troncature du second ordre

${\displaystyle \mathrm {E_{t}} =\left|{\frac {f''(x)}{2}}\right|h}$

Par ailleurs, l'ordinateur commet une erreur d'arrondi : la précision relative étant r, la précision absolue sur ƒ(x) est |ƒ(x)|r, et donc l'erreur induite sur la dérivée

${\displaystyle \mathrm {E_{a}} ={\frac {|f(x)|r}{h}}}$

L'erreur totale vaut donc

${\displaystyle \mathrm {E} =\mathrm {E_{t}} +\mathrm {E_{a}} =\left|{\frac {f''(x)}{2}}\right|h+{\frac {|f(x)|r}{h}}}$ Cette fonction est convexe, et admet un minimum en

${\displaystyle {\bar {h}}={\sqrt {\frac {2r|f(x)|}{|f''(x)|}}}}$

Cela dépend donc du rapport entre la valeur de ƒ et la courbure ƒ". Pour les zones où la fonction ƒ est « modérée » — c'est-à-dire que ƒ/ƒ" est de l'ordre de l'unité —, on peut retenir

${\displaystyle {\bar {h}}\simeq {\sqrt {r}}}$.

一个实值函数的图像曲线。函数在一点的导数等于它的图像上这一点处之切线的斜率。

导数（英语：Derivative）是微积分学中重要的基础概念。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。导数的本质是通过极限的概念对函数进行局部的线性逼近。当函数的自变量在一点上产生一个增量时，函数输出值的增量与自变量增量的比值在趋于0时的极限如果存在，即为在处的导数，记作、或。例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。

导数是函数的局部性质。不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。如果函数的自变量和取值都是实数的话，那幺函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。

对于可导的函数，也是一个函数，称作的导函数。寻找已知的函数在某点的导数或其导函数的过程称为求导。反之，已知导函数也可以倒过来求原来的函数，即不定积分。微积分基本定理说明了求原函数与积分是等价的。求导和积分是一对互逆的操作，它们都是微积分学中最为基础的概念。

定义

一般定义 设有定义域和取值都在实数域中的函数 。若 在点 的某个邻域内有定义，则当自变量 在 处取得增量 （点 仍在该邻域内）时，相应地函数 取得增量 ；如果 与 之比当 时的极限存在，则称函数 在点 处可导，并称这个极限为函数 在点 处的导数，记为 ，即： 也可记作 、 、 或 。 对于一般的函数，如果不使用增量的概念，函数 在点 处的导数也可以定义为：当定义域内的变量 趋近于 时， 的极限。也就是说， 几何意义 当函数定义域和取值都在实数域中的时候，导数可以表示函数的曲线上的切线斜率。如右图所示，设为曲线上的一个定点，为曲线上的一个动点。当沿曲线逐渐趋向于点时，并且割线的极限位置存在，则称为曲线在处的切线。 若曲线为一函数的图像，那幺割线（蓝色）的斜率为： 当处的切线（红色），即的极限位置存在时，此时，，则的斜率为： 上式与一般定义中的导数定义完全相同，也就是说，因此，导数的几何意义即曲线在点处切线的斜率。 导数、导函数与微分算子 若函数 在其定义域包含的某区间 内每一个点都可导，那幺也可以说函数 在区间 内可导，这时对于 内每一个确定的 值，都对应着 的一个确定的导数值，如此一来就构成了一个新的函数，这个函数称作原来函数 的导函数，记作：、 或者 。值得注意的是，导数是一个数，是指函数 在点 处导函数的函数值。但在不至于混淆的情况下，通常也可以说导函数为导数。 由于对每一个可导的函数 ，都有它的导函数 存在，我们还可以定义将函数映射到其导函数的算子。这个算子称为微分算子，一般记作 或 。例如： 由于微分算子的输出值仍然是函数，可以继续求出它在某一点的取值。比如说对于函数 ， 所以，。 导数与微分 微分也是一种线性描述函数在一点附近变化的方式。微分和导数是两个不同的概念。但是，对一元函数来说，可微与可导是完全等价的。可微的函数，其微分等于导数乘以自变量的微分，换句话说，函数的微分与自变量的微分之商等于该函数的导数。因此，导数也叫做微商。函数的微分又可记作。

历史

导数和积分的发现是微积分发明的关键一步。十七世纪以来，光学透镜的设计以及炮弹弹道轨迹的计算促使欧洲的数学家对曲线的切线进行研究。1630年代，法国数学家吉尔·德·罗伯瓦尔作出了最初的尝试。与此同时，同是法国人的费马在计算切线时已经使用了无穷小量的概念。 如右图，费马考虑曲线 在 处的切线。他声称，对于切线，有以下的关系成立： 对上式变形后得到： 对于具体的函数 ，比如 ，费马计算 的值，并将 设为0，就得到 ，从而确定切线的斜率。可以看出，费马的方法实质上已经是求导。费马还给出了 为多项式时切线的公式。英国的巴罗、荷兰的于德（Johnann Van Waveren Hudde）和瓦隆的斯卢兹（René Francoiss Walther de Sluze）继续了费马的工作。然而，费马和巴罗等人并没有将求导归纳为一种独立的工具，只是给出了具体的计算技巧。 十七世纪六十年代，英国人伊萨克·牛顿提出了“流数”的概念。牛顿在写于1671年的《流数法与无穷级数》中对流数的解释是：“我把时间看作是连续的流动或增长，而其他的量则随着时间而连续增长。我从时间流动性出发，把所有其他量的增长速度称为流数。”也就是说，流数就是导数。牛顿将无穷小的时间间隔定义为“瞬”（moment），而一个量的增量则是流数与瞬的乘积。求导数时，牛顿将自变量和因变量两边展开，同时除以瞬，再将剩下的项中含有瞬的项忽略掉。而在他的第三篇微积分论文中，牛顿使用了新的概念：最初比和最后比。他说： “ 随我们的意愿，流数可以任意地接近于在尽可能小的等间隔时段中产生的增量，精确地说，它们是最初增量的最初的比，它们也能用和它们成比例的任何线段来表示。 ” 相比于牛顿，德国数学家莱布尼兹使用了更清晰的记号来描述导数（见导数的记法一节）。他利用了巴罗的“微分三角形”概念，将自变量和因变量的增量记为 和 。他把 理解为“比任何给定的长度都要小”，而 则是 移动时 “瞬刻的增长”。而导数则是两者之间的比例。他还研究了函数之和、差、积、商的求导法则。 伊萨克·牛顿爵士 牛顿和莱布尼兹的差别在于，牛顿将无穷小量作为求流数或导数的工具，而莱布尼兹则用无穷小量的比值来表示导数。这与二人的哲学思想差异有关。 微积分的理论面世后，遭到了有关无穷小量定义的攻击与质疑。导数的定义自然也包括在内。莱布尼兹和牛顿对无穷小量的认识都是模糊的。不仅如此，莱布尼兹甚至引入了 和 ，称其为“未消失的量”，用以进行求导前部的计算。在完成计算后再用“消失的量” 和 来代替它们，并假定前两者之比等于后两者之比，认为这是一个不容置疑的真理。 许多数学家，包括伯努利兄弟、泰勒、麦克劳林、达朗贝尔、拉格朗日和欧拉都想要对微积分的严密性辩护或将微积分严密化。但受限于对无穷小量的认识，十八世纪的数学家并没有做出太大的成果。微积分的强烈抨击者，英国的乔治·贝克莱主教在攻击无穷小量时认为，流数实际上是“消失的量的鬼魂”，是0与0之比。欧拉承认后者，并认为0与0之比可以是有限值。拉格朗日则假定函数都可以展开为幂级数，并在此基础上定义导数。 十九世纪后，随着对函数连续性和极限的更深刻认识，微积分终于趋于严谨。波尔查诺是首先将导数定义为函数值的改变量与自变量增量之比在自变量增量无限接近0时趋向的量。波尔查诺强调导数不是0与0之比，而是前面的比值趋向的数。柯西在他的著作《无穷小分析教程概论》中也使用了同样的定义，并定义 为导数与 的乘积。这样，导数和微分的概念得到了统一。

导数的记法

从微积分发轫至如今，不同的数学家都曾使用过不同的记号来表示函数的导数。部分记号至今仍然使用，成为现代的通用记法。 牛顿的记法 作为微积分的发明人之一，牛顿在1704年著作中将导数用函数符号上方的点来表示。例如 的导数就记作，而二阶导数则记为。他以后的数学家也会将用来表示函数的微分。牛顿的记法中没有明确自变量，因此 对 的导数在牛顿的著作中也会被记成，因为这可以理解为两个函数 和 对于另一个变量 的导数比。而这个导数比（使用莱布尼兹的记号）： 牛顿的记号多见于物理学或与之有关的方面，如微分方程中。以及直到现在，使用函数符号上加一点来表示某一变量的变化率（即对时间的导数）依然常见于各类物理学教材中（如使用来表示加速度等）。注意到对于高阶的导数，这种记法就无法表示了。 莱布尼兹的记法 戈特弗里德·威廉·莱布尼茨 莱布尼兹在他的研究中分别使用 和 来表示函数自变量和应变量（输出值）的有限变化量，而使用 和 来表示“无限小”的变化量（即所谓的“无穷小量”）。如果将函数记为的话，那幺在莱布尼兹的记法下，其导数记为： 、、 或 这个记法最早出现在莱布尼兹1684年的论文中，莱布尼兹在之前的文章中会将 记成 ，把 记成 。莱布尼兹记法的好处是明确了自变量和应变量。要注意的是记号是一个整体，也是，而可以看成一个整体，也可以不严谨地看成和的比值。此外， 表示的是导函数，在某一点 的导数则记为： 对于更高阶的导数（比如说n阶，见高阶导数一节），莱布尼兹的记法是： 、 或 这种记法是在1695年出现的。这里的分子和分母不再具有单独的意义。莱布尼兹的记法中使用 来表示微分算子，比如说二阶的导数 就可以看成： 莱布尼兹记法的另一个好处是便于记忆导数计算的法则。例如链式法则（见导数的计算一节）应用莱布尼兹的记法就是： 可以想象为右边是两个分式的乘积，消去之后就变成左边。 由于牛顿和莱布尼兹之间关于微积分创始人称号的持久纠纷，在十八世纪早期的很长时间里，英国数学界与欧洲大陆的数学界分别采用牛顿和莱布尼兹的记号，泾渭分明。这种情况直到十八世纪后期才开始改变，随着拉格朗日记法的出现而变得多样化起来。 拉格朗日的记法 另一种现今常见的记法是十八世纪拉格朗日于1797年率先使用的，以在函数的右上角加上一短撇作为导数的记号。函数 的导数就记作 或 。二阶和三阶导数记为、 和 、。如果需要处理更高阶的导数，则用括号内的求导阶数n来代替短撇，记为：、。当十九世纪的数学家柯西处理微分学时，他认为莱布尼兹的记法“模糊不便”，而采用更为“紧凑”的记法，将 记为。这种记法可说是拉格朗日记法的变种。后来这种记法曾继续被精简为。 其它记法 十九世纪以前，尽管大部分数学家会选择采用牛顿、莱布尼兹或拉格朗日的记号来表示导数，但也有很多的数学家希望使用自己的方法来记录。在不同数学家的著作中可以看到各种主流记法的混合或变体。数学家之间关于什幺样的记法最为简便和严谨也是各执一词。同时，由于函数的微分、导数、偏导数以及无穷小量等概念尚未成熟，记号的不统一更增加了数学家之间相互理解的难度。十九世纪初期的德国数学家马尔丹·欧姆采用来表示导数，而同时期的雅可比则采用来表示偏导数。同时许多数学家采用、或 表示偏导数。 用大写字母表示导数从十八世纪末就开始。1800年，法国数学家路易斯·弗朗索瓦·安托内·阿伯加斯特（Louis François Antoine Arbogast）使用表示函数 的m阶导数或全微分。而其后本杰明·佩尔斯（Benjamin Peirce）也使用表示 对 的导数。而柯西也采用类似的记号，用表示函数 对 的m阶偏导数。

函数可导的条件

如果一个函数的定义域为全体实数，即函数在上都有定义，那幺该函数是不是在定义域上处处可导呢？答案是否定的。函数在定义域中一点可导需要一定的条件。首先，要使函数在一点可导，那幺函数一定要在这一点处连续。换言之，函数若在某点可导，则必然在该点处连续。这个结论来自于连续性的定义。 证明： 设函数上一点，函数在这一点可导，即存在，其中 所以： 即函数在处连续。 符号函数（sgn函数）是一个不连续的函数在断点处不可导的例子： 首先注意到这个函数在处不连续。作为验证，可以求出函数在处附近的变化率，根据函数可导的条件再进行判断： 该函数在左侧附近的变化率为： 当时，上面的比值趋于正无穷大发散，不存在，故这个符号函数在处不可导。 然而，连续性并不能保证可导性。即使函数在一点上连续，也不一定就在这一点可导。事实上，存在着在每一点都连续，但又在每一点都不可导的“病态函数”。1931年，斯特凡·巴拿赫甚至证明，事实上“绝大多数”的连续函数都属于这种病态函数（至少在一点可导的连续函数在所有连续函数中是贫集）。在连续而不可导的函数里，一种常见的情况是，函数在某一点连续，并且可以定义它的左导数和右导数： 左导数： 右导数： 然而左导数和右导数并不相等，因而函数在该处不可导。实际上，若函数导数存在，则必然可以推出左右导数相等，这是由极限的性质（极限存在则左右极限相等）得来： 下面以绝对值函数作为例子： 该函数在处的左导数为： 该函数在处的右导数为： 绝对值函数在处的左右导数皆存在，但由于左右导数不相等，故绝对值函数在处不可导。 如果函数在一点的左右导数都存在并且相等，那幺函数在该处可导。

导数与函数的性质

通过认识可导函数的导数，可以推断出不少函数本身的性质。 单调性 x变化时函数（蓝色曲线）的切线变化。函数的导数值就是切线的斜率，绿色代表其值为正，红色代表其值为负，黑色代表值为零。 根据微积分基本定理，对于可导的函数，有： 如果函数的导函数在某一区间内恒大于零（或恒小于零），那幺函数在这一区间内单调递增（或单调递减），这种区间也称为函数的单调区间。导函数等于零的点称为函数的驻点（或极值可疑点），在这类点上函数可能会取得极大值或极小值。进一步判断则需要知道导函数在附近的符号。对于满足 的一点 ，如果存在 使得 在区间 上都大于等于零，而在区间 上都小于等于零，那幺 是一个极大值点，反之则为极小值点。而如果存在 使得 在区间 上都大于等于零或都小于等于零，那幺称这个点为拐点。 如果函数在 处的二阶导数 存在，极值点也可以用它的正负性判断（已确定）。如果，那幺 是一个极小值点，反之为极大值点。 凹凸性 可导函数的凹凸性与其导数的单调性有关。如果函数的导函数在某个区间上单调递增，那幺这个区间上函数是向下凸的，反之则是向上凸的。如果二阶导函数存在，也可以用它的正负性判断，如果在某个区间上 恒大于零，则这个区间上函数是向下凸的，反之这个区间上函数是向上凸的。

导数的计算

常见的多项式函数就是基本函数之一。如果，其中是非零实数，那幺导函数。函数的定义域可以是整个实数域，但导函数的定义域则不一定与之相同。例如当 时：

底数为的指数函数 的导数还是自身： 而一般的指数函数 的导数还需要乘以一个系数：

三角函数的导数仍然是三角函数，或者由三角函数构成:

反三角函数的导数则是无理分式:

求导的线性性：对函数的线性组合求导，等于先对其中每个部分求导后再取线性组合。

两个函数的乘积的导函数，等于其中一个的导函数乘以另一者，加上另一者的导函数与其的乘积

两个函数的商的导函数也是一个分式。其中分子是分子函数的导函数乘以分母函数减去分母函数的导函数乘以分子函数后的差，而其分母是分母函数的平方。

复合函数的求导法则：如果有复合函数 ，那幺

高阶导数

（莱布尼兹公式）

多元函数的导数

矢量值函数的导数 当函数 的取值不再是实数，而是一般的中的矢量时，仍然可能对其求导。这时的函数值是：。每个 都是一个实数值的函数。具体的例子如二维或者三维空间里的参数方程。因此，对 求导实际上是对每个分量函数 求导。 这也符合定义 设为的一组基，那幺对函数： 其导函数为： 偏导数 如果有函数 其自变量不是单个实数，而是多于一个元素，例如： 这时可以把其中一个元素（比如 ）看做参数，那幺 可以看做是关于另一个元素的参数函数： 也就是说，对于某个确定的 ，函数 就是一个关于 的函数。在 固定的情况下，可以计算这个函数 关于 的导数。 这个表达式对于所有的 都对。这种导数称为偏导数，一般记作： 这里的符号 ∂ 是字母 的圆体变体，一般读作 的首音节或读“偏”，以便与 区别。 更一般地来说，一个多元函数 在点 处对 的偏导数定义为： 上面的极限中，除了 外所有的自变元都是固定的，这就确定了一个一元函数： 因此，按定义有： 偏导数的实质仍然是一元函数的导数。 多变量函数的一个重要的例子，是从（例如 或 ）映射到上的标量值函数 。在这种情况下， 关于每一个变量 都有偏导数。在点 ，这些偏导数定义了一个矢量： 。 这个矢量称为 在点 的梯度。如果 在定义域中的每一个点都是可微的，那幺梯度便是一个矢量值函数 ，它把点 映射到矢量 。这样，梯度便决定了一个矢量场。 方向导数 方向导数是比偏导数更加广泛的概念。导数的本质是函数值增量与自变量增量之比的极限。在多元函数 中，可以选定一个确定的方向（以这个方向上的单位矢量 表示），并考虑函数在这个方向上的增量： 这个增量为关于 的一元函数。函数 的方向导数定义为这个增量与 的比值在 趋于0时的极限，记为。 方向导数表示了函数从某点开始在某个方向上的变化率。 在中，如果将矢量 选为正规基 之中的一个，如，那幺方向导数就是关于 的偏导数。

推广

导数的概念创建在变量为实数之上，但也可以推广到更加广泛的意义上。推广的导数本质上仍旧是函数在局部一点上的线性逼近。 复变量导数 对于变量为复数的函数，也可以定义导数的概念。假设有复变函数。如果 在某一点 及附近有定义，并且极限： 存在，那幺就说函数 在 可导。其中 表示 的模长趋向于0。如果将复变量 视作 ，那幺 可以视作一个上的函数。如果作为复变函数的 可导，那幺作为上函数的 的偏导数也存在，但反之则不然。只有当柯西-黎曼条件满足的时候才能保证复变函数的复可导性。 弱微分 在分布理论里，弱微分的概念使得对更多严格意义上无法求导的函数也可以定义导函数。设是一个局部勒贝格可积（比如说在中）的函数，称是的一个弱微分，如果对所有的测试函数，都有： 成立。其中测试函数是指紧支撑的光滑函数。弱微分包括了强微分，也就是通常意义上的导数。 次导数 过的直线（红）在函数（蓝）下方，它的斜率是函数的次导数 在凸分析，也就是对凸函数的研究中，可以定义凸函数的次导数。次导数的概念是导数的几何意义的推广。由于函数是凸的，过它的图像上每一点总可以作一条直线，使得函数的图像在直线上方。这种直线的斜率称为函数在这点的次导数。如果函数在某点可导，那幺次导数只有一个，等于其导数。如果函数像绝对值函数一样在零点有突然的转折，那幺次导数可能不止一个。比如过零点而斜率在之间的直线都在绝对值函数下方，因此之间的每个数都是绝对值函数在零点的次导数。 非整数阶导数 早在十九世纪，在数学家明确了求导与积分的互逆关系以后，就出现了负阶次导数的记号：（表示求n次积分）。而非整数阶导数的概念则进一步将其推广。比如，半微分算子表示其作用于函数上两次以后的效果将等于一次求导： 定义非整数阶导数的方法不止一种，最常用的非整数阶导数定义为黎曼-刘维尔定义： 设，函数 的s阶积分为： 而对，函数 的阶导数为： 加托导数和弗雷歇导数 方向导数在无穷维矢量空间如巴拿赫空间和弗雷歇空间上可以推广为加托导数和弗雷歇导数。二者都经常用于形式化泛函导数的概念，常见于物理学，特别是量子场论。 导子 微分代数中有导子的概念。导子是具备了微分算子的某些特征的运算子，例如矢量场的李导数，或非交换代数中的交换子。给定一个环或域 上的一个代数 ， 上的一个-导子 是一个从 射到自身的-线性映射（线性自同态），并满足导数的乘积法则： 所有-导子构成了 上线性自同态集 的子空间。

导数的应用

物理学、几何学、工程科学、经济学等学科中的一些重要概念都可以用导数来表示。如，导数可以表示运动物体的瞬时速度和加速度，也可以表示曲线在一点的斜率。 边际和弹性 经济学中，所谓边际和弹性的概念与导数紧密相关。比如边际成本就是产量增加一个单位所带来的成本的增加，若将其连续化，得到的便是成本函数的导数。又如需求的弹性是指价格变化一个单位时，需求量的变化，连续化后相应的也是需求函数关于价格的导数。