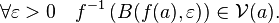En mathématiques, la continuité est une propriété topologique d'une fonction. En première approche, une fonction f est continue si, à des variations infinitésimales de la variable x, correspondent des variations infinitésimales de la valeur f(x).
La continuité est associée à la notion de continuum dont l'origine est géométrique. Dans un continuum géométrique, comme le plan ou l'espace, un point peut se déplacer continument pour s'approcher à une précision arbitraire d'un autre point. La notion de continuité est définie de manière rigoureuse en mathématiques.
Le premier exemple de fonctions continues concerne des fonctions réelles définies sur un intervalle et dont le graphe peut se tracer sans lever le crayon. Cette première approche donne une idée de la notion (la fonction ne saute pas) mais n'est pas suffisante pour la définir, d'autant plus que certains graphes de fonctions pourtant continues ne peuvent pas se tracer de cette manière, telles par exemple des courbes ayant des propriétés fractales comme l'escalier de Cantor.
Historiquement définie pour des fonctions de la variable réelle, la notion de continuité se généralise à des fonctions entre espaces métriques ou entre espaces topologiques, sous une forme locale et sous une forme globale.
L'étude des fonctions continues se révèle fructueuse pour les propriétés qu'elles possèdent (propriété de convergence au sens où « lim(f(x)) = f(lim(x)) », théorème des valeurs intermédiaires, théorème des bornes, intégrabilité…).
Définition pour les fonctions réelles
Définition — Soient I un intervalle réel, une fonction définie sur I à valeurs réelles et . La fonction f est dite continue en a si :
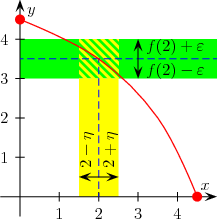
Exemple d'une fonction continue sur un intervalle
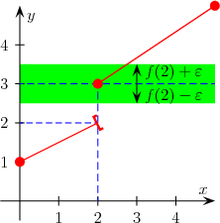
Exemple d'une fonction non continue en 2
:
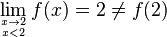
ƒ n'est pas continue à gauche en 2.
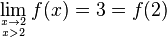 f
f est continue à droite en 2.
Ainsi f est continue en a si et seulement si la limite de f en a existe (elle vaut alors nécessairement f(a)).
Cela veut dire que si l'on se fixe un seuil ε, on peut trouver un intervalle autour de a tel que f(x) soit à une distance inférieure à ε de f(a).
Si la continuité est valable uniquement à droite (pour x > a), on dit que f est continue à droite en a. De même à gauche pour a. Dire que f est continue en a revient à dire qu'elle l'est à droite et à gauche en a.
La fonction f est dite continue (sur I) si elle est continue en tout point a de I. Une fonction qui présente des « sauts » est discontinue. La notion de saut est illustrée sur la figure ci-contre, elle correspond à l'existence d'une limite à droite et d'une limite à gauche qui n'ont pas toutes les deux la même valeur que f(a).
Commentaire
C'est l'idée du seuil ε fixé à l'avance qui est importante. Cette définition est le fruit des efforts des mathématiciens du XIX siècle pour rendre rigoureuse la notion intuitive de continuité. En analyse non standard, une approche plus intuitive est possible : on dira que f est continue en a si f(x) – f(a) est infiniment petit quand x – a est infiniment petit. Tout repose alors sur une définition rigoureuse des infiniment petits et cette définition ne s'applique qu'aux fonctions dites standards.
La définition globale de la continuité dans le cadre des espaces topologiques (voir plus bas) permet elle aussi de s'affranchir des ε, mais ceci au prix du formalisme de la topologie générale.
Exemples
Une grande partie des fonctions usuelles sont continues sur leur domaine de définition : fonctions polynômes, rationnelles, exponentielles, logarithmes, hyperboliques, trigonométriques, racine n-ième, puissance n-ième, valeur absolue.
La fonction partie entière sur les réels est discontinue : on « lève le crayon » en arrivant à chaque entier.
Une fonction réelle dérivable en un point est continue en ce point. (La réciproque est fausse : cf. § « Des erreurs à éviter ».)
Il existe des fonctions définies sur ℝ qui ne sont continues en aucun point : c'est le cas de la fonction indicatrice de ℚ, appelée la fonction de Dirichlet, qui vaut 1 en tout point rationnel et 0 ailleurs. Intuitivement, on voit bien que, pour tracer cette fonction, il faudrait « lever le crayon » une infinité de fois par intervalle, et surtout aucune ligne de longueur non nulle ne peut être tracée.
Cet exemple « pathologique » se généralise : pour tout ensemble Fσ (c'est-à-dire toute réunion d'une suite de fermés) d'un intervalle fermé non trivial I de ℝ, il existe une application de I dans ℝ dont les points de discontinuité sont exactement les éléments de cet ensemble (c'est en fait une caractérisation des Fσ).
Propriétés
La notion de continuité sur un intervalle pour les fonctions réelles
est utile pour prouver l'existence de solutions à des équations de la forme f(x) = m (voir théorème des valeurs intermédiaires) ;
simplifie le calcul de limites car .
La composée de fonctions continues est une fonction continue. La composée d'une fonction continue et d'une suite convergente est une suite convergente.
Les propriétés de stabilité de la continuité par combinaison linéaire (i.e. pour tous α, β réels et f, g fonctions réelles continues, la fonction αf + βg est continue) et par produit de deux fonctions font de l'ensemble des fonctions continues une algèbre sur le corps des réels.
Des erreurs à éviter
Une fonction dérivable en un point est continue en ce point mais la réciproque est fausse. Par exemple les fonctions racine carrée et valeur absolue sont continues en 0 mais non dérivables en ce point (voir l'article « Dérivabilité »).
Des fonctions telles que f : x ↦ 1/x ou tan(x) sont bel et bien continues. L'erreur consistant à dire que f n'est pas continue en 0 est renforcée par l'absence de précision sur son domaine de définition : la continuité en un point situé hors du domaine de définition n'a pas de sens. Dans le cas de f, tant qu'une valeur n'est pas précisée pour f(0), on doit supposer que le domaine de définition considéré est ℝ*. Ainsi, dire que f est ou n'est pas continue en 0 n'a aucun sens ; on peut seulement dire qu'elle n'est pas prolongeable par continuité en une fonction continue en 0.
Dans l'histoire, la continuité d'une fonction était pensée comme « ne pouvant pas passer d'une valeur à une autre sans passer par toutes les valeurs intermédiaires » (propriété souvent appelée PVI pour « propriété des valeurs intermédiaires ») mais on sait aujourd'hui qu'il n'y a pas équivalence entre les deux : la fonction f : x ↦ sin(1/x) prolongée par 1 en 0 vérifie bien la propriété des valeurs intermédiaires et est pourtant discontinue en zéro.
Définition dans le cas des espaces métriques
La droite réelle est un espace métrique, la distance usuelle sur R étant celle qui à deux nombres associe la valeur absolue de leur différence. La définition ci-dessus se généralise donc naturellement :
Définition
Définition — Soient (E, d) et (E', d') deux espaces métriques, ƒ une application de E dans E' et a un point de E.
On dit que l'application ƒ est continue au point a si :
-
![\forall \varepsilon > 0 \quad \exists \eta > 0 \quad \forall x \in E \quad \Big[d(x,a)<\eta \Rightarrow d'(f(x),f(a))<\varepsilon\Big].](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/f1509b69e63ae1cb25fe5c745038c2fb.png)
À nouveau, ƒ est ainsi continue en a si et seulement si la limite de ƒ en a existe (elle vaut alors nécessairement ƒ(a)).
Exemples
Toute application uniformément continue entre deux espaces métriques — en particulier toute application lipschitzienne — est continue.
Une application linéaire d'un espace vectoriel normé vers un autre est continue si et seulement si elle est bornée sur la boule unité (et elle est alors lipschitzienne).
C'est toujours le cas si l'espace de départ est de dimension finie, mais le cas non borné se présente en dimension infinie : considérons comme application linéaire la dérivation sur l'espace ℝ[X] des polynômes réels, en choisissant, comme norme d'un polynôme, la somme des valeurs absolues de ses coefficients. Tous les monômes X sont de norme 1. Pourtant leurs polynômes dérivés sont de la forme nX, donc de norme n avec n arbitrairement grand. Donc la famille des dérivées n'est pas bornée, et la dérivation n'est pas une application continue.
Définition générale (espaces topologiques)
On donne deux définitions équivalentes dans le cas des espaces topologiques.
Définition locale
On peut faire reposer la définition locale (c'est-à-dire pour un point) de la continuité sur la notion de limite :
Définition — Soient E et F deux espaces topologiques, f une application de E dans F et a un point de E.
La fonction f est dite continue au point a si f(a) est une limite de f en ce point.
Si F est séparé comme tout espace métrique, ou même seulement T1, il suffit pour cela qu'il existe une limite de f en ce point.
La notion de seuil utilisée pour les fonctions réelles est généralisée par la notion de voisinage : désigne l'ensemble des voisinages de a, et ceux de f(a). On démontre alors :
Théorème — La fonction f est continue au point a si et seulement si l'image réciproque de tout voisinage W de f(a) est un voisinage de a, ce qui s'écrit : Il suffit pour cela que cette propriété soit vérifiée pour tout W d'une base de voisinages de f(a), par exemple pour tout W ouvert contenant f(a).
La fonction f est dite continue sur E (ou simplement : continue) si elle est continue en tout point de E. Elle est dite continue sur une partie A de E si sa restriction à A (muni de la topologie induite) est continue (il suffit pour cela que f soit continue en tout point de A).
Caractérisations globales
On peut déduire de la définition locale trois caractérisations équivalentes des applications qui sont continues (en tout point de l'espace de départ).
La première d'entre elles est qu'une application est continue si et seulement si l'image réciproque de tout ouvert de l'espace d'arrivée est un ouvert de l'espace de départ. La suivante, analogue, s'écrit en termes de fermés. L'avant-dernière utilise les notions d'adhérence et d'image directe et la dernière celles d'adhérence et d'image réciproque.
Le lien avec la notion intuitive est le suivant : quand une fonction « saute », cela signifie que des points très proches de l'espace de départ, se retrouvent sur des points très éloignés à l'arrivée. Or pour une application continue, ces sauts sont impossibles, car si l'on considère un point du départ et son image à l'arrivée, on sait que tout un voisinage de ce point de départ doit arriver au voisinage du point d'arrivée.
f est continue en tout point de E
pour tout ouvert O de F, f(O) est un ouvert de E ;
pour tout fermé G de F, f(G) est un fermé de E ;
pour toute partie A de E , f( A ) est inclus dans f(A) ;
pour toute partie B de F, f(B) est inclus dans f( B ).
1 ⇔ 2 : d'après la définition locale, f est continue en a ssi pour tout ouvert O de F tel que a appartienne à f(O), f(O) est voisinage de a. Donc f est continue en tout point ssi pour tout ouvert O de F, f(O) est voisinage de chacun de ses points, c'est-à-dire est ouvert.
2 ⇔ 3 : par passage aux complémentaires.
3 ⇒ 5 : en posant G = B.
5 ⇒ 4 : en posant B = f(A) et en utilisant le fait que A est inclus dans f (f(A)).
4 ⇒ 3 : en posant A = f (G) et en utilisant le fait que f(f (G)) est inclus dans G.
Les caractérisations 2 et 3 sont souvent utilisées, a contrario, pour montrer qu'un certain ensemble est ouvert (ou fermé) en faisant intervenir une application qu'on sait déjà être continue. Par exemple : Dans R, l'hyperbole d'équation xy = 1 est fermée, comme image réciproque du singleton {1} par l'application continue « produit » : R → R, (x, y) ↦ xy. Le graphe d'une application continue f : E → F est fermé dans E×F dès que F est séparé. Deux applications continues à valeurs dans un espace séparé qui coïncident sur une partie dense sont égales.
Dans R, l'hyperbole d'équation xy = 1 est fermée, comme image réciproque du singleton {1} par l'application continue « produit » : R → R, (x, y) ↦ xy.
Le graphe d'une application continue f : E → F est fermé dans E×F dès que F est séparé.
Deux applications continues à valeurs dans un espace séparé qui coïncident sur une partie dense sont égales.
Dans les caractérisations 4 et 5, les inclusions réciproques sont fausses en général. Par exemple si f est l'application continue de R dans R qui à x associe 1 si x ≤ 1 et 1/x si x ≥ 1, 0 n'appartient pas à f(R) alors qu'il appartient à f(R), et n'appartient pas à f (]0, 1[) alors qu'il appartient à f (]0, 1[).
D'après ce théorème, toute restriction-corestriction d'une application continue est continue (pour les topologies induites).
Ce théorème permet aussi de montrer que si E est une réunion d'ouverts tels que la restriction de f à chacun de ces ouverts soit continue alors f est continue, et de même si E est réunion d'un nombre fini de fermés tels que la restriction de f à chacun de ces fermés soit continue. Pour une réunion (même finie) de « parties quelconques », on n'a aucun résultat de ce genre.
Exemples
Une application constante d'un espace topologique dans un autre est continue. En effet, l'image réciproque de toute partie est soit l'ensemble vide, soit l'ensemble de départ tout entier.
Toute application dont l'espace de départ est muni de la topologie discrète, ou l'espace d'arrivée de la topologie grossière, est continue.
L'application identité, d'un ensemble muni d'une certaine topologie vers le même ensemble muni d'une autre topologie, est continue si et seulement si la topologie sur l'ensemble de départ est plus fine que celle sur l'ensemble d'arrivée. La bijection réciproque n'est alors pas continue, sauf si les deux topologies sont égales.
Soient A une partie d'un espace topologique X, et 1A sa fonction caractéristique : de X dans ℝ (ou, par corestriction, de X dans la paire {0, 1} munie de la topologie discrète), les points de X en lesquels 1A est discontinue sont les points de la frontière de A ; de X dans l'espace de Sierpiński (la paire {0, 1} munie de la topologie { ∅, {1}, {0, 1} }), les points de X en lesquels 1A est discontinue sont alors seulement les points de A non intérieurs à A.
de X dans ℝ (ou, par corestriction, de X dans la paire {0, 1} munie de la topologie discrète), les points de X en lesquels 1A est discontinue sont les points de la frontière de A ;
de X dans l'espace de Sierpiński (la paire {0, 1} munie de la topologie { ∅, {1}, {0, 1} }), les points de X en lesquels 1A est discontinue sont alors seulement les points de A non intérieurs à A.
Équivalence de la définition métrique et topologique
Un espace métrique (E, d) possède une topologie associée τ. Pour tout point a de E, les boules ouvertes de centre a et de rayons strictement positifs forment une base de voisinage de a pour cette topologie. Si τ' désigne la topologie associée à un espace métrique (E', d'), alors :
Propriété — Une fonction f de (E, d) dans (E', d') est continue en un point de E si et seulement si elle est continue en ce point, considérée comme une fonction de (E, τ) dans (E', τ').
En effet, la fonction est continue en a du point de vue topologique si et seulement si (en utilisant les d'-boules formant une base de voisinages de f(a)) : 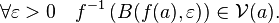 En utilisant les d-boules formant une base de voisinages de a, cette condition se réécrit :
En utilisant les d-boules formant une base de voisinages de a, cette condition se réécrit :  ou encore :
ou encore :  ce qui correspond exactement à la définition de la continuité formalisée par les distances.
ce qui correspond exactement à la définition de la continuité formalisée par les distances.
Notion de continuité dans l'histoire
La continuité n'a pas toujours été définie de la façon précédente.
Euler dans son Introductio in analysin infinitorum définit la fonction continue comme une fonction définie par une seule expression analytique finie ou infinie (série entière) et appelle fonctions discontinues ou mixtes celles possédant plusieurs expressions analytiques suivant les intervalles. Sylvestre Lacroix (1810) appelle fonction continue une fonction dont toutes les valeurs sont définies à partir d'une même loi ou dépendent d'une même équation. Cette notion de continuité s'appelle la continuité eulérienne et est plus restrictive que la définition actuelle. Par exemple, la fonction définie pour tout réel négatif par f(x) = x et tout réel positif par f(x) = x est continue au sens actuel et mixte (discontinue) au sens d'Euler.
La définition que nous utilisons aujourd'hui est celle donné par Bernard Bolzano dans sa théorie des fonctions : « La fonction f(x) varie suivant la loi de continuité pour la valeur x si la différence |f(x + w) – f(x)| peut-être rendue plus petite que toute valeur donnée. » (Prague 1816).
Augustin Louis Cauchy dans son Cours d'analyse de l'école royale polytechnique, définit la continuité en x par : f est continue en x si la valeur numérique de la différence f(x + a) – f(x) décroit indéfiniment avec celle de a, utilisant ainsi les notions des infiniment petits.
Une autre définition de la continuité, inspirée de celle de Cauchy est de dire que f est continue en a si pour tout suite (xn) convergeant vers a, la suite f(xn) converge vers f(a). Cette définition de la continuité par les suites n'est équivalente à la définition moderne que sur un espace séquentiel.
Malgré cette définition formelle, l'utilisation de la continuité reste au début du XIX siècle grandement intuitive quand on voit Cauchy tenir le raisonnement suivant, pour démontrer le théorème des valeurs intermédiaires : « La fonction f étant continue entre les points x0 et x, la courbe qui a pour équation y = f(x) sera continue entre les points (x0, f(x0)) et (x, f(x)) et la droite d'équation y = b qui passera entre les ordonnées f(x0) et f(x) ne peut que rencontrer dans l'intervalle la courbe mentionnée. »
Il existe aussi une notion de continuité plus forte : la continuité uniforme dans laquelle la distance |f(x) – f(x')| peut être rendue aussi petite que l'on veut pour n'importe quel couple (x, x') tels que la distance | x – x' | soit suffisamment faible. Contrairement à la continuité classique (continuité en un point a fixé), la continuité uniforme assure que la majoration est vraie sans avoir besoin de fixer a. Cette notion fut précisée par Edouard Heine en 1872.

 词典释义:
词典释义:
 ,
, 逐;
逐; ,坚贞
,坚贞 ;
;
 ;
; , 继续音
, 继续音
 adj. f 【电】直流电
adj. f 【电】直流电
 引
引 引弓, 持续
引弓, 持续 引钳
引钳 引
引

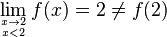
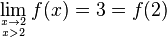
![\forall \varepsilon > 0 \quad \exists \eta > 0 \quad \forall x \in E \quad \Big[d(x,a)<\eta \Rightarrow d'(f(x),f(a))<\varepsilon\Big].](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/f1509b69e63ae1cb25fe5c745038c2fb.png)