Le monocorde est un instrument de musique constitué d'une caisse de résonance et d'une corde unique séparée en deux parties par un chevalet mobile. Il sert en particulier à comprendre les rapports de hauteurs entre les intervalles musicaux .
Histoire
Boèce attribue l'invention du monocorde en tant qu'instrument expérimental à Pythagore, mais il existait probablement avant en Égypte.
Pythagore a fait la démonstration que la hauteur , du son est inversement proportionnelle à la longueur de la corde. De cette expérience, Pythagore tire les conclusions suivantes :
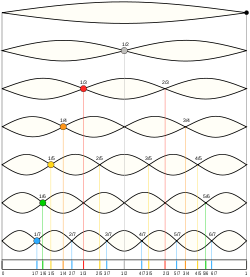
En plaçant le chevalet au milieu de la corde tendue — donc, en divisant celle-ci en deux —, la corde en question donne l'octave supérieure du son initial. On obtient cette même note des deux côtés du chevalet.
De la même façon, en plaçant le chevalet au tiers de la corde — donc, en divisant celle-ci en trois —, la corde en question donne alors le redoublement de la quinte supérieure du son initial (autrement dit, la « douzième supérieure »). De l'autre côté du chevalet, avec une longueur de , on obtient "tout naturellement" la quinte supérieure du son initial.
Théorie
En divisant la corde en intervalles égaux de 2 à 6 on obtient les principaux accords purs :
par 2 : c'est l'octave supérieure par rapport à la corde entière (rapport 2/1) ;
par 3 : c'est la quinte (rapport 3/2) ;
par 4 : c'est la quarte (rapport 4/3) ;
par 5 : c'est la tierce majeure (rapport 5/4) ;
par 6 : c'est la tierce mineure (rapport 6/5).
Soit 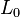 la longueur de la corde, et
la longueur de la corde, et  sa fréquence ; Pythagore a donc remarqué que
sa fréquence ; Pythagore a donc remarqué que 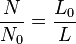 .
.
On remarque aussi que 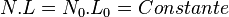
Comme 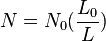 , la pratique arithmétique grecque fait noter les nombres rationnels plus grands que 1 comme 1 + X.
, la pratique arithmétique grecque fait noter les nombres rationnels plus grands que 1 comme 1 + X.
En posant 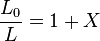 , on obtient
, on obtient 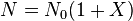
d'où on déduit 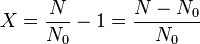 , la notation revient donc à nommer X, depuis X = 0 pour le do à X=1 pour le do de l'octave supérieur.
, la notation revient donc à nommer X, depuis X = 0 pour le do à X=1 pour le do de l'octave supérieur.
On déduit aussi :
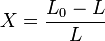 et
et 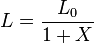
Pour un 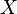 donné, on voit que la corde est partagée en deux longueurs :
donné, on voit que la corde est partagée en deux longueurs : 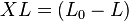 et
et 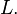
Or 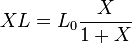
Par exemple, si la corde à vide donne un Do, le Sol a pour fréquence N = No ( 1 + 1/2 ). Il se joue donc avec la frette au [(1/2/(1+1/2)]=1/3 de la longueur ).
Les sept notes de la gamme correspondaient à des rationnels "simples" et approximatifs d'une assonance.
Le tableau ci-après donne les valeurs X, encadrant 1+1/2 == 1+5/10( qu'on pourra réduire aisément) et les écarts (rapport de fréquences de deux notes consécutives) ; il apparaît que ces écarts ne sont évidemment pas constants, et il y a un problème à régler simplement l'écart entre les notes ( l'écart musical  , irrationnel, conduira à la crise majeure des mathématiques, appelée crise pythagoricienne).
, irrationnel, conduira à la crise majeure des mathématiques, appelée crise pythagoricienne).
| Note | do | ré | mi | fa | sol | la | si | do | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X | 0 | 1/8 | 1/4 | 1/3 | 1/2 | 2/3 | 7/8 | 1 | ||||||||
| 1 + X | 1 | 1 + 1/8 | 1 + 2/8 | 1 + 3/9 | 1 + 5/10 | 2 - 3/9 | 2 - 1/8 | 2 | ||||||||
| Rapport | 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2 | ||||||||
| Ecarts | 9/8 | 10/9 | 9/8 | 10/9 | 9/8 | |||||||||||
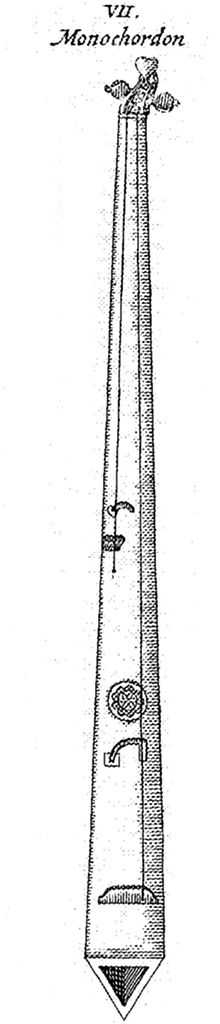
Variétés actuelles de monocordes
Đàn bầu (ou đàn độc huyền)
Duxianqin
Ichigenkin
Monocorde à clavier
单弦乐器,或称独弦琴,是一类弦乐器和实验室仪器,一般只有一根弦,但有些称为「单弦乐器」(monochord)的乐器会有超过一根弦。一个 monochord是一种古老的的音乐和科学实验室仪器。 “monochord”一词来自希腊文和,字面意思是“一个弦。”很多单弦乐器除了有一个开弦外,还一个可移动的弦柱。
种类
独弦琴 中国独弦琴 京族独弦琴(弹匏) 日本一弦琴(一弦琴)
中国独弦琴
京族独弦琴(弹匏)
日本一弦琴(一弦琴)
迪德里一弦(diddley bow)
艾克塔拉(ektara)
拨铃波琴(Berimbau)
独弦押琴(海号独弦琴、Tromba marina)

 词典释义:
词典释义:

 琴,一
琴,一 琴
琴

 塞绳,
塞绳, 软
软

 的
的
 琴,
琴,
 琴
琴 〉
〉 调的,不变的
调的,不变的
 ,
,

 调的歌
调的歌 调的;
调的;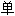 塞绳,
塞绳,  软
软