L'intrication quantique (ou enchevêtrement quantique) est un phénomène observé en mécanique quantique dans lequel l'état quantique de deux objets doit être décrit globalement, sans pouvoir séparer un objet de l'autre, bien qu'ils puissent être spatialement séparés. Lorsque des objets quantiques sont placés dans un état intriqué (ou état enchevêtré), il existe des corrélations entre les propriétés physiques observées de ces objets qui ne seraient pas présentes si ces propriétés étaient locales. En conséquence, même s'ils sont séparés par de grandes distances spatiales, deux objets intriqués O1 et O2 ne sont pas indépendants et il faut considérer {O1+O2} comme un système unique.
L'intrication quantique a un grand potentiel d'applications dans les domaines de l'information quantique, tels que la cryptographie quantique, la téléportation quantique ou l'ordinateur quantique. En même temps, elle est au cœur des discussions philosophiques sur l'interprétation de la mécanique quantique. Les corrélations prédites par la mécanique quantique, et observées dans les expériences, montrent que la nature n'obéit pas au principe du « réalisme local » cher à Einstein, selon lequel les propriétés observées d'un système, bien définies avant toute mesure, sont attribuables à ce système et ne peuvent changer que par interaction avec un autre système.
Historique
Le caractère surprenant des états intriqués a pour la première fois été souligné par Einstein, Podolsky et Rosen dans un article de 1935 qui tentait de montrer que la mécanique quantique était incomplète. Dans cet article, les auteurs décrivent une expérience de pensée qui restera connue comme le paradoxe EPR.
Définition
Il est plus aisé de définir ce qu'est un état non intriqué, ou séparable, que de définir directement ce qu'est un état intriqué.
État pur
Dans le cas où le système global {S1+S2} peut être décrit par un vecteur d'état, son état est un vecteur de l'espace de Hilbert . Certains états peuvent s'écrire sous la forme d'un produit tensoriel entre un état de S1 et un état de S2 :
-
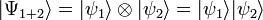
Ces états sont appelés états séparables ou factorisables. Le système S1 est dans un état quantique clairement identifié, 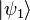 , qui n'est pas altéré par les mesures effectuées sur S2.
, qui n'est pas altéré par les mesures effectuées sur S2.
Un état intriqué est par définition un état non séparable, qui s'écrit en général sous la forme
-
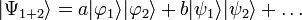
C'est donc une superposition d'états d'un système biparti. Pour illustrer la différence entre états séparables et intriqués, supposons par exemple que forme une base de l'espace , et une base de l'espace . L'état :
-
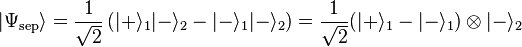
est un état séparable, puisqu'il peut être factorisé comme indiqué ci-dessus, tandis que l'état :
-
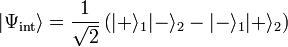
est un état intriqué.
Démonstration Si était un état factorisable, on devrait pouvoir l'écrire sous la forme générale : où , , et sont quatre nombres complexes. Dans le second membre, le premier terme représenterait l'état du sous-système S1 dans l'espace , et le second terme représenterait l'état du sous-système S2 dans l'espace . On obtient alors le système suivant : Pour que l'équation (1) soit vérifiée, il est nécessaire soit que , ce qui est incompatible avec (3), soit que , ce qui est incompatible avec (4). Le système ci-dessus n'a donc pas de solution, montrant que l'état n'est pas factorisable.
Par suite, il existe des états a priori légitimes d'un système global {S1 + S2} qui ne peuvent pas s'écrire sous la forme du produit tensoriel d'un état d'un sous-système S1 par un état d'un sous-système S2 ; pour de tels états intriqués, il est donc impossible de parler de « l'état de S1 » : seul le système global {S1 + S2} a un état défini, état défini par le premier membre de la relation ci-dessus. En un sens, il n'est plus possible de séparer conceptuellement les deux systèmes.
La principale caractéristique de l'état est qu'il y a corrélation parfaite des mesures réalisées sur S1 avec les mesures réalisées sur S2. Ainsi, supposons que l'on mesure l'état de S1 dans la base « +/– » et que l'on trouve « + » (ce qui peut arriver aléatoirement dans 50 % des cas). Le système total {S1+S2} est alors projeté dans l'état , de sorte que la mesure de S2 donnera "–" avec certitude, même si les deux mesures sont séparées par un intervalle de genre espace dans l'espace-temps. Einstein décrivait ce phénomène comme une « action surnaturelle à distance », car tout se passe comme si la mesure effectuée sur S1 à un instant donné avait un effet absolument instantané sur le résultat de la mesure effectuée sur S2 même si les deux événements ne sont pas reliés causalement, c'est-à-dire même si une information partant de S1 et se déplaçant à la vitesse de la lumière n'a pas le temps d'informer S2 du résultat de la mesure sur S1. De fait, un système intriqué forme absolument un tout, qui ne peut pas être séparé en deux systèmes indépendants tant qu'il reste intriqué, quelle que soit l'étendue spatiale de ce système. Voir ci-dessous les conséquences philosophiques que cela peut avoir, ainsi que l'article relatif au paradoxe EPR et celui relatif à l'expérience d'Aspect au cours de laquelle des états intriqués d'un système de deux photons ont été produits en laboratoire pour la première fois, chaque photon représentant l'un des deux sous-systèmes S1 et S2 du système global {S1 + S2} constitué par l'ensemble des deux photons.
État mixte
Expérimentalement, il n'est pas possible de préparer un état quantique bien déterminé avec une reproductibilité de 100 %. Pour tenir compte de cette préparation imparfaite, on décrit l'état du système par une matrice densité, qui pondère chaque état pur par la probabilité de produire cet état : . On peut donc se demander quelle est la définition d'un état séparable décrit par une matrice densité. Un premier choix serait de définir les états séparables comme étant ceux qui s'écrivent :
-
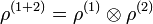 .
.
Ces états sont effectivement séparables, car il n'y a aucune corrélation entre les mesures faites sur S1 et celles faites sur S2, mais la définition peut être étendue, et l'écriture la plus générale pour la matrice densité d'un état séparable est :
-
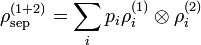 ,
,
où 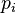 est une loi de probabilité (
est une loi de probabilité (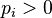 et
et 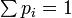 ).
).
Cette définition présente l'avantage d'inclure les systèmes corrélés classiquement dans les états séparables. Supposons par exemple une expérience qui produise deux particules simultanément, et aléatoirement une fois sur deux un état , et une fois sur deux un état . L'état ainsi produit est représenté par la matrice . Alternativement, on peut imaginer un physicien facétieux qui envoie chaque jour deux lettres, l'une contenant un signe « + » et l'autre contenant un signe « – », à deux de ses collègues (1 et 2), mais en faisant correspondre aléatoirement les lettres et les adresses. Les mesures réalisées sur S1 seront parfaitement corrélées à celles réalisées sur S2 : si la mesure donne « + » pour un système, on est sûr que la mesure de l'autre système donnera « – ». Cependant, ces corrélations ne sont pas de nature quantiques : elles existent dès la production des deux particules et ne proviennent pas du fait que l'on mesure l'état du système. En particulier, si l'on changeait de base de mesure en utilisant une observable ne commutant pas avec l'observable « signe », on s'apercevrait que l'état ainsi produit ne viole pas les inégalités de Bell. Les résultats sont donc différents de ceux obtenus avec l'état intriqué décrit précédemment.
Dans le formalisme de la matrice densité, un état intriqué est simplement défini comme un état qui n'est pas séparable. Dans le cas général, même lorsque l'on connaît la matrice densité d'un système, il est difficile de dire si l'état obtenu est intriqué ou séparable. Une condition nécessaire est de regarder si la « transposée partielle » de la matrice densité est positive. Pour les dimensions 2 et 3, cette condition est également suffisante.
Implications philosophiques
Les états intriqués prévus par la mécanique quantique ont, depuis, été observés en laboratoire et leur comportement correspond à celui que prévoit la théorie. Cela fait d'elle une théorie physique non-locale.
Par contre, on démontre que les états intriqués ne peuvent pas être utilisés pour transmettre une information quelconque d'un point à un autre de l'espace-temps plus rapidement qu'avec de la lumière. La raison est que le résultat de la mesure relatif à la première particule est toujours aléatoire, dans le cas des états intriqués comme dans le cas des états non-intriqués : il est donc impossible de « transmettre » quelque information que ce soit, puisque la modification de l'état de l'autre particule, pour instantanée qu'elle soit, conduit à un résultat de la mesure relatif à la seconde particule qui est toujours aussi aléatoire que celui relatif à la première particule ; les corrélations entre les mesures des deux particules resteront indétectables tant que les résultats des mesures ne seront pas comparés, ce qui implique nécessairement un échange d'information classique, respectueux de la relativité. Par suite, la mécanique quantique est bien également parfaitement compatible avec le principe de causalité.
Entropie et mesure
Dans un état maximalement intriqué, il y a corrélation complète de l'état de S1 avec celui de S2, de sorte que l'entropie de (S1 union S2) est simplement celle de S2 ou de S1. Il y a sous-additivité complète.
ER = EPR
Juan Maldacena et Leonard Susskind, deux physiciens américains, ont imaginé une théorie reliant deux phénomènes découverts tout deux par Einstein : les « ponts d'Einstein-Rosen » (ou trous de ver) et l'intrication quantique. D'après les deux scientifiques, éloigner deux particules intriquées reviendrait en fait à creuser un pont ER autour d'une seule et même particule qui manifesterait ses propriétés à plusieurs endroits de l'espace-temps.
Cette théorie apporte un éclairage sur un problème appelé paradoxe EPR qui met en évidence la non-localité de la mécanique quantique, et l'oppose au principe de localité qui est le fondement de la théorie de la relativité. Cependant, cette correspondance ER/EPR n'est démontrée que dans un modèle d'univers très simplifié, où la gravité est générée en l'absence de masse.
Réalisation pratique d'un état intriqué
Les candidats technologiques d'intricats sont nombreux :
Le premier système historiquement étudié est la paire de photons EPR, étudiée par Alain Aspect, puis par l'équipe genevoise de Nicolas Gisin.
Un atome de Rydberg couplé à une cavité microonde réalise un autre système intriqué expérimentalement performant. Les calculs sont conduits en toute précision ; mais la décohérence n'y est pas nulle ; sa complexité expérimentale ne permet pas d'espoir technologique sérieux.
Un état intriqué a également été démontré pour des chaînes d'ions piégés dans un piège de Paul et pour des spins nucléaires sur une molécule en solution.
Le quantronium de Saclay est aussi un système où l'intrication a été observée.
Les systèmes utilisant des boîtes quantiques
Les systèmes utilisant la spintronique
Codes correcteurs d'erreurs
L'informatique quantique a beaucoup progressé depuis que l'on sait réaliser des intricats de faible décohérence : il est devenu pensable de prévoir l'avenir d'un futur ordinateur quantique. Les mathématiciens (Shor, Kitaev...) ont fondé le calcul quantique, qui est en train de révolutionner au début du XXI siècle le calcul de la complexité algorithmique et ont montré que l'on pouvait restaurer leur pureté par l'intermédiaire de codes correcteurs d'erreurs qui pallieraient la décohérence.
Ces codes sont en 2009 sujets à d'intenses recherches. L'avenir de l'information quantique leur est directement liée, et avec elle, le monde de l'informatique quantique.

 词典释义:
词典释义:
 ,二元
,二元 ;
;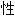 ;
;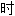 存
存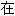 ;
;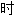
 ;
;
 ,
,
 ;
; ;
;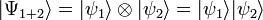
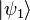 , qui n'est pas altéré par les mesures effectuées sur S2.
, qui n'est pas altéré par les mesures effectuées sur S2.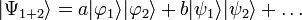
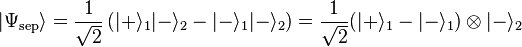
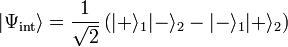
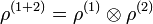 .
.
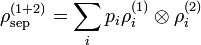 ,
,
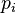 est une loi de probabilité (
est une loi de probabilité (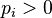 et
et 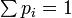 ).
).