Chaque rangée est une permutation des trois billes de couleur.
En mathématiques, la notion de permutation exprime l'idée de réarrangement d'objets discernables. Une permutation d'objets distincts rangés dans un certain ordre correspond à un changement de l'ordre de succession de ces objets.
La permutation est une des notions fondamentales en combinatoire, c'est-à-dire pour des problèmes de dénombrement et de probabilités discrètes. Elle sert ainsi à définir et à étudier le carré magique, le carré latin, le sudoku, ou le Rubik's Cube. Les permutations servent également à fonder la théorie des groupes, celle des déterminants, à définir la notion générale de symétrie, etc.
Définition et exemples
Définition
Une permutation d'un ensemble X est une bijection de X sur lui-même.
Notamment, une permutation de n éléments (où n est un entier naturel) est une bijection d'un ensemble fini de cardinal n sur lui-même.
Exemples
Une permutation de l'alphabet de 26 lettres est un mot de 26 lettres contenant chaque lettre une fois et une seule ; et il est clair que cette définition reste valable pour n'importe quel alphabet de n lettres, avec des mots de longueur n.
Il y a beaucoup d'ordres différents (720) dans lesquels six cloches, de différentes notes, peuvent être sonnées les unes après les autres. Si les cloches sont numérotées de 1 à 6, alors chaque ordre possible peut être représenté par une liste de 6 nombres, sans répétition, par exemple (3, 2, 6, 5, 1, 4).
De la même façon, six livres posés sur un rayonnage et numérotés de 1 à 6, peuvent être permutés de différentes manières : rangement par ordre alphabétique, ordre alphabétique inverse, ordre de préférence, ou ordre choisi « au hasard ». Chacun de ces réarrangements peut être vu comme une bijection de l'ensemble des six livres, ou de façon identique, une bijection de l'ensemble {1, 2, … ,6} sur lui-même. En effet, si l'ordre final des livres est 3,2,6,5,1,4, on peut définir l'application f : « est remplacé par » ainsi
-
1 est remplacé par 3 soit f(1)=3
-
2 est remplacé par 2 soit f(2)=2
-
3 est remplacé par 6 soit f(3)=6
-
4 est remplacé par 5 soit f(4)=5
-
5 est remplacé par 1 soit f(5)=1
-
6 est remplacé par 4 soit f(6)=4
Finalement, les objets effectivement permutés comptent peu : la permutation peut être ramenée à une permutation de nombres : les numéros des livres ou les numéros de cloches.
Supposons que n personnes s'assoient sur n chaises différentes numérotées de 1 à n disposées sur une même rangée. Nous pouvons considérer un placement de ces n personnes sur les chaises, comme une bijection de l'ensemble des n personnes sur lui-même, indiquant la façon dont les personnes sont placées les unes par rapport aux autres sur les chaises.
Une permutation de n éléments est aussi appelée permutation sans répétition de ces éléments. Signalons qu'autrefois, une permutation était appelée substitution.
Dénombrement des permutations
Soit X un ensemble fini à n éléments. Le problème est de compter les permutations de X, c'est-à-dire les bijections de X dans lui-même. Comme pour les exemples précédents, on peut toujours numéroter les éléments de X de 1 à n. Dénombrer les permutations de X revient à dénombrer tous les réarrangements possibles de la liste, c'est-à-dire tous les n-uplets formés d'entiers de 1 à n dans un certain ordre.
Il est possible de donner une liste de tous ces réarrangements, sous forme d'une représentation arborescente : il y a n choix pour le premier terme de la liste. Puis pour chacun de ces premiers choix, il y a n–1 possibilités pour le deuxième choix, n–2 pour le troisième, ainsi de suite. Finalement il y a n! (factorielle de n) choix possibles pour constituer une liste. Cette méthode permet d'énumérer une et une seule fois chaque permutation.
Si X est un ensemble fini de cardinal n, alors l'ensemble des permutations de X est fini, de cardinal n!.
Lorsque n=0, le résultat reste encore valable puisqu'il existe une seule application de l'ensemble vide dans lui-même et qu'elle est bijective.
Il est possible de dénombrer plus généralement les p-arrangements de n éléments, ou encore les applications injectives d'un ensemble de cardinal fini p dans un ensemble de cardinal fini n. Ce nombre d'arrangements se note An et le cas des permutations apparaît comme le cas particulier n=p.
Notation des permutations
Soit X un ensemble fini, de n éléments. Quitte à effectuer une numérotation, permuter les éléments de X revient à permuter les entiers de 1 à n. La notation traditionnelle des permutations place les éléments qui vont être permutés dans l'ordre naturel sur une première ligne, et les images en correspondance, sur une deuxième ligne. Par exemple
-
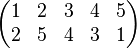
est l'application 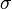 définie par
définie par
-
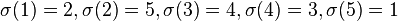 ,
,
ou schématiquement
-
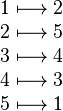 .
.
Toutefois, la notation la plus pratique est la forme « canonique » (voir ci-dessous). Sous cette forme, la permutation précédente s'écrit :
-
(1 2 5)(3 4),
ce qui signifie 1 donne 2 (c.-à-d., 2 est l'image de 1) qui donne 5 qui donne 1 ; 3 donne 4 qui donne 3. Cette écriture correspond à la décomposition sous la forme d'une composition de permutations circulaires de supports disjoints.
Le support d'une permutation σ est l'ensemble des éléments x tels que σ(x) est différent de x. La permutation σ se restreint donc en l'identité sur le complémentaire de son support, et en une permutation sans point fixe sur son support.
Permutations particulières
Identité :
La permutation de X qui envoie chaque élément sur lui-même est l'application identité de X.
Transposition :
Une permutation qui échange deux éléments distincts i et j en laissant tous les autres inchangés est appelée transposition. On utilise fréquemment une notation allégée pour désigner cette permutation : (i j). Il convient de remarquer qu'avec ce choix de notations, (i j)=(j i). Une transposition élémentaire échange deux éléments voisins, (i i+1).
Permutation circulaire :
Plus généralement, on définit les permutations circulaires ou cycles. Le p-cycle associé aux éléments distincts a1, … , ap (pris dans cet ordre) envoie l'élément a1 sur a2, puis a2 sur a3 etc. et enfin ap sur a1. Tous les autres éléments restent inchangés. Un tel cycle se note habituellement sous la forme (a1 … ap). Là encore, (a1 … ap)=(a2 … ap a1)=…
Propriétés algébriques
Composition de permutations
Les permutations de X sont définies comme des applications de X dans X, il est donc possible de définir leur produit de composition, qui se note ∘ (mais ce signe est le plus souvent omis). Précisément, pour deux permutations σ et σ', appliquer σ' puis σ revient à appliquer une permutation σ"=σ∘σ' appelée le produit de σ et σ'.
La notation des permutations est bien adaptée au calcul du produit de composition. Ainsi en prenant par exemple
-
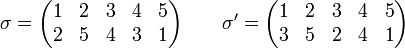
Le calcul du produit peut être présenté sur trois lignes. La première et la deuxième ligne présentent l'effet de la première permutation 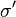 , puis on fait correspondre aux éléments de la deuxième ligne leur image par
, puis on fait correspondre aux éléments de la deuxième ligne leur image par 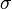 .
.
-
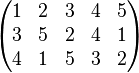
Soit, finalement, en rayant la ligne de calcul intermédiaire
-
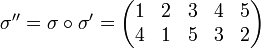
Il est à rappeler que la loi de composition n'est pas commutative (dès que l'ensemble X a au moins 3 éléments) mais deux permutations de supports disjoints commutent.
Structure de groupe
Soient n éléments distincts dans un certain ordre. Appliquer une permutation σ revient à en modifier l'ordre. Revenir à l'ordre initial se fait aussi par une permutation ; celle-ci est notée σ. Plus généralement, cette application σ, est la bijection réciproque de σ, puisqu'appliquer σ puis σ, ou σ puis σ, revient à appliquer la permutation identique. La permutation σ s'appelle la permutation réciproque ou permutation inverse de σ.
Soit X un ensemble quelconque. L'ensemble S(X) des permutations de X est un groupe pour la loi de composition ∘, appelé groupe symétrique de X. Dans le cas particulier où X={1, …, n} avec n entier naturel, cet ensemble se note Sn.
Si nous considérons un ensemble fini X de cardinal n (formé d'éléments qui ne sont pas nécessairement des entiers), nous pouvons numéroter les éléments de X et identifier les permutations des éléments de X avec les permutations des n premiers entiers.
Décompositions des permutations
Décomposition en produit de transpositions
Toute permutation de support fini peut être décomposée en un produit de transpositions. Par exemple, cela signifie qu'on peut, par des échanges deux à deux, modifier à volonté l'ordre des cartes d'un paquet.
Comme deux transpositions (i j) et (k l) concernant quatre éléments différents commutent, une telle décomposition n'est pas unique. De plus, une transposition est une involution, on peut donc également ajouter un échange de deux cartes, puis l'échange des deux mêmes cartes. En revanche on démontre que la parité du nombre de transpositions nécessaire reste la même. Ceci permet de définir la parité et la signature d'une permutation.
Une permutation paire est une permutation qui peut être exprimée comme le produit d'un nombre pair de transpositions. Une définition équivalente est que sa décomposition en cycles disjoints donne un nombre pair (éventuellement nul) de cycles de longueurs paires. Une permutation impaire est une permutation qui peut être exprimée comme produit d'un nombre impair de transpositions.
La permutation identique est une permutation paire car elle peut être considérée comme le produit de 0 transposition, selon la convention sur le produit vide.
La permutation circulaire (1 2 … p) est le produit des transpositions (1 p)(1 p-1)…(1 3)(1 2). La décomposition en produits de cycles disjoints (voir ci-dessous) implique donc la décomposition en produit de transpositions.
La transposition (i j) est la composition des transpositions élémentaires (i i+1)(i+1 i+2)…(j-1 j)(j-2 j-1)…(i i+1) ce qui montre que toute permutation est décomposable en un produit de transpositions élémentaires. C'est un outil utile pour visualiser une permutation.
Algorithme de décomposition
Voici l'étape générale d'un algorithme de décomposition d'une permutation σ de support fini {1,…,n}.
si la permutation est l'identité elle est produit de 0 transposition.
sinon il est possible de considérer le premier point non fixe par σ
-
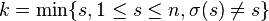
Alors en appelant τ la transposition qui échange k et σ(k), on forme σ1=τ∘σ et on reprend l'algorithme avec σ1.
On forme ainsi des permutations σ1, σ2 etc. obtenues en multipliant σ par une succession de transpositions τ1, τ2 etc., jusqu'à atteindre la permutation identique. Alors il vient
-
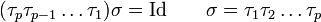
La validité de l'algorithme se justifie en remarquant que la position du premier point non fixe augmente strictement à chaque étape, jusqu'à ce que tous les points soient fixes. L'algorithme se conclut après au plus n–1 opérations, puisque si les n–1 premiers points sont fixes, ils le sont tous.
Ainsi il est possible d'affirmer plus précisément que toute permutation peut s'écrire comme produit d'au plus n–1 transpositions. En outre, le nombre minimum de transpositions nécessaires pour écrire une permutation donnée est exactement celui obtenu avec cet algorithme.
L'algorithme ci-dessus correspond à l'algorithme de décomposition en produit de cycles disjoints suivi de l'écriture de chaque cycle comme un produit de transpositions. Le nombre minimum de transpositions nécessaires est donc égal à n–p, où p est le nombre de cycles disjoints (en comptant les points fixes comme cycles de longueur 1).
Décomposition en produit de cycles à supports disjoints
Orbite d'un élément
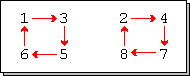
les deux cycles de la permutation σ
L'orbite d'un élément selon une permutation σ est l'ensemble de ses images successives obtenues par applications répétées de σ. Ainsi en introduisant la permutation σ
-

L'élément 1 a pour images successivement 3,5,6 puis de nouveau 1,3,5 etc. L'orbite de 1 est donc l'ensemble {1,3,5,6}. L'orbite de 3 est également l'ensemble {1,3,5,6}, mais l'orbite de 2 est {2,4,7,8}.
Plus généralement, pour une permutation quelconque, les orbites sont disjointes et forment une partition de l'ensemble {1,2,…,n}. En restriction à une orbite donnée de taille p, la permutation se comporte comme une permutation circulaire des p éléments.
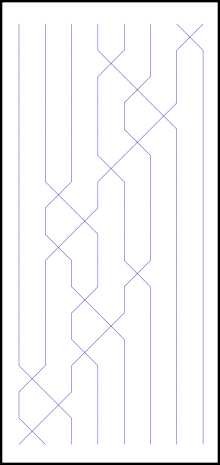
Le diagramme de la permutation σ comme produit de transpositions élémentaires se lit de haut en bas.
Décomposition
Pour décrire la permutation, il suffit de prendre un élément dans chaque orbite et de donner l'ordre de succession de ses images par itération de σ. Ainsi toujours avec le même exemple, la permutation σ peut s'écrire sous la forme d'une succession des deux cycles (1 3 5 6) et (2 4 7 8). L'ordre des cycles n'importe pas mais l'ordre des éléments à l'intérieur d'un cycle doit être respecté jusqu'à l'obtention d'un cycle complet. Ainsi, la même permutation peut être écrite par exemple
-
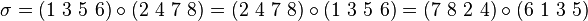
Dans cette notation on omet souvent le symbole de composition ∘ pour alléger l'écriture.
La décomposition « canonique » d'une permutation en « produit » de cycles s'obtient en plaçant d'abord le plus petit nombre en première position dans chaque cycle et en ordonnant les cycles selon leur premier élément. Cette notation omet souvent les points fixes, c'est-à-dire les éléments qui sont leur propre image par la permutation; ainsi la permutation (1 3)(2)(4 5) s'écrit simplement (1 3)(4 5), puisqu'un cycle d'un seul élément n'a aucun effet.
Si, au contraire, on place le plus petit nombre en dernière position dans chaque cycle, sans omettre les points fixes, on obtient une suite de nombres, liée aux nombres de Stirling, qui permet l'analyse combinatoire du nombre de cycles et de la taille des cycles d'une permutation : c'est la correspondance fondamentale de Foata.
Applications
De nombreuses propriétés de la permutation σ peuvent se lire facilement sur la décomposition en cycles disjoints :
la signature de σ est le produit des signatures : elle vaut (-1)=(-1), où p est le nombre de cycles disjoints (en comptant les points fixes comme cycles de longueur 1) et q est le nombre de cycles de longueur paire.
l'ordre de σ (en tant qu'élément du groupe symétrique) est le plus petit entier k>0 tel que σ est l'identité. Il est égal au PPCM des longueurs des cycles.
le théorème des restes chinois est clairement illustré par les puissances de σ. Il est plus facile à énoncer quand les longueurs des cycles sont premières entre elles : dans ce cas, l'ordre de σ est le produit des longueurs des cycles et le groupe engendré par les puissances de σ est isomorphe à ℤ/nℤ qui lui-même est décomposable en produit des ℤ/niℤ, chaque cycle avançant à son rythme pour ne retomber en phase qu'au produit.
la conjuguée d'une permutation π par une permutation σ est la permutation σ∘π∘σ. On peut aisément calculer cette permutation, en remplaçant chaque élément i dans la décomposition en cycles disjoints de π par σ(i).
Articles connexes
Permutation avec répétition
Permutation aléatoire
Matrice de permutation
Nombre de Stirling
Théorème de réarrangement de Riemann
Code de Lehmer
Correspondance fondamentale de Foata
Matrice de Costas
Portail des mathématiques

 词典释义:
词典释义:
 ,对
,对
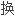 ,转
,转
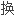

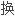
 ;
;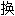 ;
;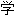 】
】

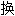
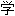 】排列;
】排列;

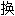
 ; 对
; 对 ; 开-关; 轮值; 排列
; 开-关; 轮值; 排列 排列;
排列; 

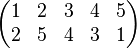
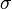 définie par
définie par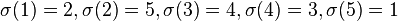 ,
,
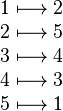 .
.
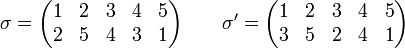
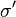 , puis on fait correspondre aux éléments de la deuxième ligne leur image par
, puis on fait correspondre aux éléments de la deuxième ligne leur image par 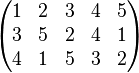
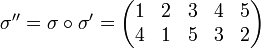
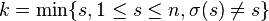
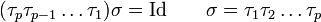



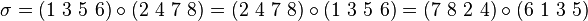

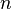 个元素的有限集可以一一对应到集合
个元素的有限集可以一一对应到集合 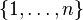 ,有限集的置换可以化约到形如 {1, ..., n} 的集合之置换。此时有两种表示法。
,有限集的置换可以化约到形如 {1, ..., n} 的集合之置换。此时有两种表示法。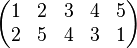
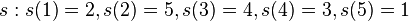 。
。 。对任一元素
。对任一元素  ,由于集合有限而
,由于集合有限而 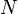 使得
使得 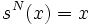 ,故可将置换
,故可将置换 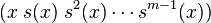 ,其中
,其中 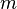 是满足
是满足 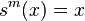 的最小正整数。
的最小正整数。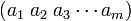 与
与

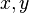 或给出同一个轮换,或给出不交的轮换。
或给出同一个轮换,或给出不交的轮换。 理解为一类特殊的置换:仅须定义置换
理解为一类特殊的置换:仅须定义置换 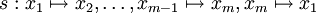 ,而在其它元素上定义为恒等映射。不交的轮换在函数合成的意义下可相交换。
,而在其它元素上定义为恒等映射。不交的轮换在函数合成的意义下可相交换。