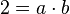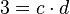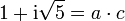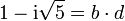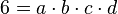En mathématiques, et plus particulièrement en algèbre, un idéal est un sous-ensemble remarquable d'un anneau : c'est un sous-groupe du groupe additif de l'anneau et qui est de plus stable par multiplication par les éléments de l'anneau. À certains égards, les idéaux s'apparentent donc aux sous-espaces vectoriels — qui sont des sous-groupes additifs stables par une multiplication externe ; à d'autres égards, ils se comportent comme les sous-groupes distingués — ce sont des sous-groupes additifs à partir desquels on peut construire une structure d'anneau quotient.
Apparus à la fin du XIX siècle en théorie algébrique des nombres pour généraliser à des entiers algébriques la décomposition en facteurs premiers des entiers, les idéaux ont rapidement joué un rôle central en algèbre et en géométrie algébrique, en particulier à la suite des travaux d'Emmy Noether isolant l'importance des conditions de chaîne. Au-delà de l'algèbre ils interviennent de façon centrale dans les développements du XX siècle de certains chapitres d'analyse fonctionnelle, notamment l'étude des algèbres de Banach et l'analyse harmonique commutative.
En algèbre commutative deux types d'idéaux sont omniprésents : les idéaux maximaux et, sans doute encore davantage, les idéaux premiers. Dans l'anneau des entiers relatifs, tant les idéaux maximaux que les idéaux premiers (non nuls) sont les pZ, où p est un nombre premier ; dans les anneaux commutatifs plus abstraits ces familles d'idéaux généralisent la notion de nombre premier.
En théorie des anneaux non commutatifs, il faut prendre garde à l'existence juxtaposée de deux concepts distincts d'idéaux : les idéaux à gauche (ou à droite), qui sont des sous-modules, et les idéaux bilatères, ceux par lesquels on peut quotienter. Alors que la structure des anneaux non commutatifs les plus généraux peut être extrêmement complexe, on a plus de prise sur ceux vérifiant les conditions de finitude découvertes par Emmy Noether et Emil Artin, à savoir des conditions de chaîne sur leurs idéaux à gauche ou à droite.
Définitions
Deux notions d'idéaux coexistent, qui coïncident dans le cas d'un anneau commutatif mais jouent des rôles bien différents sans hypothèse de commutativité de la multiplication.
Les idéaux comme sous-modules : idéaux à gauche et à droite
Une partie I d'un anneau A est appelée un idéal à gauche (respectivement à droite) de A lorsque :
I est un sous-groupe additif de A.
Pour tout a de A et tout x de I, ax ∈ I (resp. xa ∈ I). Autrement dit, on demande à I d'être stable sous multiplication à gauche (resp. à droite) par tout élément de A, même ceux qui ne sont pas dans I.
En utilisant le langage des modules, on peut définir plus brièvement un idéal à gauche (resp. à droite) comme un sous-module pour la structure de A-module à gauche (resp. à droite) sur A.
On appelle ensuite idéal bilatère de A (ou idéal tout court lorsqu'il n'y a pas de risque de confusion) toute partie de A qui est simultanément un idéal à gauche et un idéal à droite. Lorsque l'anneau est commutatif, ces notions se confondent toutes mais elles jouent des rôles très dissemblables en algèbre non commutative. De fait, bien qu'intervenant occasionnellement en théorie non commutative (ainsi dans la définition des anneaux simples), les idéaux bilatères sont dans ce contexte difficiles à manipuler, et de ce fait moins omniprésents que les idéaux à gauche ou à droite. On peut remarquer que les idéaux bilatères sont les sous-structures pour la structure de A-A-bimodule sur A.
Les idéaux comme noyaux : idéaux bilatères et anneaux-quotients
En répétant ce qui vient d'être dit pour se focaliser sur les seuls idéaux bilatères, on peut réécrire explicitement leur définition :
Une partie I d'un anneau A est appelée un idéal bilatère de A (ou idéal quand on ne craint pas de confusion, notamment en algèbre commutative) lorsque :
I est un sous-groupe additif de A ;
Pour tout a de A et tout x de I, ax ∈ I et xa ∈ I. Autrement dit, on demande à I d'être stable sous multiplication par tout élément de A (que ce soit à gauche ou à droite), même ceux qui ne sont pas dans I.
Un intérêt spécifique aux idéaux bilatères vient de ce qu'il est possible d'en donner une autre description, qui les lie au concept d'anneau quotient. Étant donné un idéal bilatère I d'un anneau A, le groupe quotient A / I peut être muni d'une structure d'anneau, pour laquelle la projection canonique est un morphisme d'anneaux, de noyau I. Réciproquement, tout noyau est un idéal bilatère. On peut synthétiser ces informations par l'énoncé suivant :
Un sous-ensemble I d'un anneau A est un idéal (bilatère) si et seulement s'il existe un morphisme d'anneaux dont A est l'anneau de départ et dont le noyau est I.
Certaines propriétés des idéaux bilatères peuvent être lues à travers la structure de l'anneau quotient : ainsi dans un anneau commutatif, un idéal bilatère est maximal si et seulement si l'anneau quotient est un corps.
Exemples d'idéaux
Si A est un anneau, {0} et A sont des idéaux de A, appelés idéaux triviaux. On appelle idéal propre un idéal différent de A.
Exemples en algèbre commutative
Les seuls idéaux dans un corps commutatif K sont les idéaux triviaux. Cette propriété caractérise les corps parmi les anneaux commutatifs.
Les idéaux de l'anneau Z des entiers relatifs sont les parties de la forme kZ, pour n'importe quel entier k. Le quotient Z/kZ est l'anneau des entiers modulo k.
Dans l'anneau K[X] des polynômes à coefficients dans un corps commutatif K, les idéaux sont les parties de la forme P(X)K[X], pour n'importe quel polynôme P(X). Si ce polynôme est irréductible, l'anneau quotient est un corps, appelé corps de rupture de P(X).
Exemples en algèbre non commutative
Les seuls idéaux à gauche dans un corps gauche sont les idéaux triviaux. Cette propriété caractérise les corps gauches parmi les anneaux non commutatifs.
Soit E un espace vectoriel de dimension finie (supérieure ou égale à 2) sur un corps (commutatif ou non). L'anneau des endomorphismes de E n'a pas d'autre idéal bilatère que les deux idéaux triviaux. En revanche, il possède des idéaux à gauche et à droite non triviaux ; pour tout sous-espace F de E, l'ensemble des endomorphismes de noyau contenant F est un idéal à gauche, tandis que l'ensemble des endomorphismes d'image contenue dans F est un idéal à droite.
Propriétés élémentaires
Inversibles et idéaux
Un idéal (à gauche, à droite ou bilatère) contient au moins un élément inversible si et seulement s'il est égal à l'anneau tout entier.
Morphismes et idéaux
Soit A et B deux anneaux et φ un morphisme d'anneaux de A dans B. Alors:
L'image réciproque d'un idéal à gauche (resp. à droite, resp. bilatère) de B sous φ est un idéal à gauche (resp. à droite, resp. bilatère) de A. On peut ainsi expliquer pourquoi un noyau est un idéal bilatère : c'est qu'il est l'image réciproque de l'idéal bilatère nul.
En ce qui concerne l'image directe d'un idéal de A, on peut seulement conclure que c'est un idéal (de même nature) du sous-anneau φ(A). Si φ n'est pas surjectif, rien n'oblige que ce soit un idéal de B : qu'on songe à φ l'inclusion canonique de A = ℤ dans B = ℚ. Alors φ(I) n'est un idéal de ℚ que si I est l'idéal nul.
Lorsque φ est surjectif, la situation est toutefois particulièrement simple :
Soit φ morphisme d'anneaux surjectif de A vers B. L'application est une bijection entre l'ensemble des idéaux à gauche (resp. à droite, resp. bilatères) de A contenant Ker(φ) et l'ensemble des idéaux à gauche (resp. à droite, resp. bilatères) de B. Sa bijection réciproque est .
Intersection d'idéaux
L'intersection de deux idéaux à gauche (resp. à droite, resp. bilatères), ou plus généralement d'une famille d'idéaux, est un idéal du même type.
Idéal engendré par un ensemble
Si P est une partie d'un anneau A, on appelle idéal à gauche (resp. à droite, resp. bilatère) engendré par P l'intersection de tous les idéaux à gauche (resp. à droite, resp. bilatères) de A contenant P. C'est donc le plus petit idéal contenant P.
On peut le décrire comme suit, les sommes étant à comprendre comme indexées par un ensemble fini :
pour l'idéal à gauche engendré noté ici (P)g :
-
 ;
;
pour l'idéal à droite engendré noté ici (P)d :
-
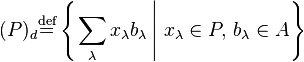 ;
;
pour l'idéal bilatère engendré noté ici (P) :
-
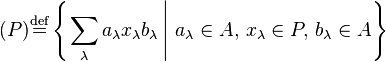 .
.
Un cas important est celui où P a un seul élément x. On parle alors de l'idéal principal (à gauche, à droite ou bilatère) engendré par x.
Somme d'idéaux
Si I et J sont deux idéaux à gauche (resp. à droite, resp. bilatères) d'un anneau A, on appelle somme de I et J l'ensemble des x + y où x parcourt I et y parcourt J.
C'est à son tour un idéal du même type. Lorsqu'on interprète les idéaux comme sous-modules, leur somme en tant qu'idéaux est le même idéal que leur somme en tant que sous-modules. La somme peut aussi être définie comme l'idéal du même type engendré par la réunion I ∪ J.
Pour l'intersection et la somme, l'ensemble des idéaux à gauche (resp. à droite, resp. bilatères) d'un anneau A est un treillis.
Plus généralement, pour une famille quelconque d'idéaux à gauche (resp. à droite, resp. bilatères)  , la somme de la famille, notée
, la somme de la famille, notée 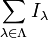 est l'ensemble des sommes
est l'ensemble des sommes 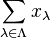 ne contenant qu'un nombre fini de termes et où
ne contenant qu'un nombre fini de termes et où 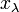 varie dans
varie dans 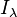 . Cet ensemble est lui aussi un idéal du même type, et c'est aussi l'idéal de ce type engendré par la réunion des
. Cet ensemble est lui aussi un idéal du même type, et c'est aussi l'idéal de ce type engendré par la réunion des  .
.
Idéaux de type fini, conditions de chaîne
Idéaux de type fini
On a déjà mentionné plus haut l’appellation d'idéal principal pour un idéal (à gauche, à droite ou bilatère) qui peut être engendré par un seul élément.
On définit plus généralement un idéal de type fini comme un idéal (à gauche, à droite ou bilatère) qui peut être engendré par une partie finie.
Conditions de chaîne sur les idéaux : anneaux noethériens et artiniens
Dans cette section on entend par « suite stationnaire » d'idéaux une suite d'idéaux 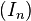 constante à partir d'un certain rang (c'est-à-dire pour laquelle il existe un n tel que
constante à partir d'un certain rang (c'est-à-dire pour laquelle il existe un n tel que 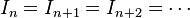 ).
).
On appelle anneau noethérien à gauche (resp. à droite) un anneau dans lequel toute suite d'idéaux à gauche (resp. à droite) croissante pour l'inclusion est stationnaire. On dit aussi qu'il vérifie la « condition de chaîne ascendante » sur les idéaux du type considéré. Cette propriété est reliée à la notion d'idéal de type fini par l'énoncé suivant, à la démonstration assez simple :
Un anneau est noethérien à gauche (resp. à droite) si et seulement si tous ses idéaux à gauche (resp. à droite) sont de type fini.
On appelle anneau artinien à gauche (en) (resp. à droite) un anneau dans lequel toute suite d'idéaux à gauche (resp. à droite) décroissante pour l'inclusion est stationnaire. On dit aussi qu'il vérifie la « condition de chaîne descendante » sur les idéaux du type considéré.
Un théorème de Hopkins et Levitzki (en), à la démonstration fort substantielle, a le corollaire suivant :
Tout anneau artinien à gauche est noethérien à gauche.
Idéaux en algèbre commutative
Les notions détaillées dans cette section admettent des généralisations en algèbre non commutative. Dans cet article d'introduction elles sont présentées dans le seul contexte d'un anneau commutatif, contexte où elles sont particulièrement pertinentes.
Produit d'idéaux
Si I et J sont deux idéaux d'un anneau commutatif, on appelle idéal produit de I et J l'idéal noté IJ engendré par l'ensemble des produits xy, où x parcourt I et y parcourt J. Il est donc égal à l'ensemble des sommes finies 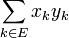 où E est un ensemble fini,
où E est un ensemble fini, 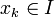 et
et 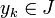 .
.
Exemple : dans l'anneau Z, le produit des idéaux 2Z et 3Z est l'idéal 6Z – donc égal à leur intersection ; en revanche le produit de l'idéal 2Z par lui-même est l'idéal 4Z.
On a toujours 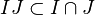 mais l'inclusion peut être stricte comme le montre l'exemple précédent.
mais l'inclusion peut être stricte comme le montre l'exemple précédent.
Quotient d'idéaux
Si I et J sont deux idéaux d'un anneau commutatif A, on appelle idéal quotient de I par J l'ensemble noté  défini par :
défini par :
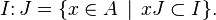
C'est un idéal de A.
Radical d'un idéal
Si est un idéal d'un anneau commutatif , on appelle radical de l'ensemble noté formé des éléments de pour lesquels il existe un entier naturel tel que . C'est un idéal de .
Idéaux premiers et idéaux maximaux
Les notions d'idéal premier et d'idéal maximal, particulièrement la première, jouent en théorie générale des anneaux un rôle similaire à celui des nombres premiers en arithmétique sur les entiers. Dans l'anneau Z des entiers relatifs, les idéaux maximaux sont exactement les pZ où p est un nombre premier ; s'y ajoute un et un seul idéal premier non maximal, l'idéal {0}.
Un idéal P d'un anneau commutatif A est appelé un idéal premier lorsque P est une partie stricte de A et, pour tous x, y de A, quand le produit xy est dans P, alors x appartient à P ou y appartient à P. Cette condition équivaut à demander à l'anneau-quotient A/P d'être intègre.
Un idéal M d'un anneau commutatif A est appelé un idéal maximal lorsqu'il existe exactement deux idéaux contenant M, à savoir A et M lui-même. Cette condition équivaut à demander à l'anneau-quotient A/M d'être un corps commutatif.
Décompositions d'un idéal
La théorie de la décomposition en facteurs premiers des entiers se reproduit dans une large classe d'anneaux commutatifs, les anneaux factoriels. Pour vaste que soit cette classe, les anneaux non factoriels sont monnaie courante, et des généralisations plus techniques de la décomposition en facteurs premiers se sont avérées des plus utiles. Même dans un cadre factoriel d'ailleurs, la décomposition d'idéaux premiers non principaux concerne aussi des idéaux non principaux sur lesquels la factorisation des éléments n'a pas de prise, et apporte donc un éclairage supplémentaire.
Décomposition d'un idéal en idéaux primaires, idéaux irréductibles
En « théorie additive » des idéaux, l'opération prépondérante est l'intersection : une décomposition d'un idéal sera une écriture de celui-ci comme intersection d'idéaux d'un type fondamental. Elle n'est pas sans parenté avec la décomposition d'un entier en facteurs entiers primaires.
Une première étape dans cette voie peut être de décomposer l'idéal en intersection d'idéaux irréductibles, où on définit un idéal irréductible comme un idéal propre I qu'on ne peut pas décomposer comme intersection de deux idéaux différents de I. Tout idéal premier est irréductible et, dans un anneau noethérien, tout idéal est intersection finie d'idéaux irréductibles.
On définit ensuite un idéal primaire I comme un idéal propre d'un anneau commutatif A vérifiant la propriété suivante : pour tous a et b de A tels que ab ∈ I, si a ∉ I alors il existe un entier naturel n tel que b ∈ I. En termes d'anneaux quotients, I est ainsi primaire si et seulement si tout diviseur de zéro dans l'anneau A / I est nilpotent.
Dans un anneau noethérien tout idéal irréductible est primaire.
On déduit de ce qui précède le théorème de Lasker-Noether :
Dans un anneau noethérien, tout idéal peut se représenter comme intersection finie d'idéaux primaires.
Il n'y a pas unicité de la représentation, même si on exige qu'elle soit minimale, mais on dispose d'énoncés qui assurent que deux représentations distinctes ne sont pas trop éloignées l'une de l'autre.
Théorie multiplicative des idéaux, anneaux de Dedekind
En exigeant davantage de l'anneau, on peut aller plus loin et décomposer un idéal par une écriture se rapprochant davantage de la factorisation des entiers en facteurs premiers ; on devra alors rechercher une écriture comme produit d'idéaux et non plus comme intersection : dans Z l'idéal pZ peut s'écrire comme produit de pZ par lui-même, mais ne pourrait pas être représenté comme une intersection d'idéaux tous différents de lui-même.
Dans un premier temps, limiter la dimension de l'anneau qu'on étudie garantit que la représentation en intersection d'idéaux primaires est aussi une représentation comme produit :
Soit A un anneau intègre noethérien de dimension 1 (c'est-à-dire où tout idéal premier non nul est maximal). Tout idéal de A peut être représenté comme produit d'idéaux primaires.
Dans un second temps, si l'anneau est en outre intégralement clos, ses idéaux primaires sont exactement les puissances d'idéaux premiers. Ceci conduit à introduire les anneaux de Dedekind, qui sont les anneaux intègres noethériens de dimension 1 intégralement clos, et mène au résultat suivant, où on a en outre unicité de la décomposition :
Soit A un anneau de Dedekind. Tout idéal de A peut être représenté de façon unique (à l'ordre des facteurs près) comme produit d'idéaux premiers.
Exemples
Dans ces exemples on note (a) l'idéal principal engendré par a, et (a,b) l'idéal engendré par a et b.
Dans Z, les décompositions des idéaux reproduisent les décompositions des entiers en facteurs primaires ou premiers. Par exemple : (180) = (4) ∩ (9) ∩ (5) = (2) (3) (5).
Dans un anneau de Dedekind non factoriel, comme Z[i√5], où l'élément 6 admet deux décompositions distinctes en irréductibles, soit 6 = 2 . 3 = (1 + i√5).(1 – i√5), les décompositions de l'idéal principal (6) font intervenir des idéaux non principaux : (6) = (2) ∩ (3, 2 + i√5) ∩ (3, 2 – i√5) = (2, 1 + i√5) (3, 2 + i√5) (3, 2 – i√5).
Dans l'anneau k[X,Y] (de dimension de Krull 2), l'idéal non primaire (X,XY)=(X) ∩ (X,Y) = (X) ∩ (X,Y) admet deux décompositions minimales distinctes comme intersection d'idéaux primaires. L'idéal primaire (X,Y) ne peut pas être représenté comme un produit d'idéaux premiers.
Dans l'anneau non intégralement clos k[T,T], l'idéal primaire (T) ne peut pas être décrit comme produit d'idéaux premiers.
L'ensemble des idéaux premiers
Effets du quotient et de la localisation
On a signalé en début d'article que le passage au quotient d'un anneau A par un idéal bilatère I induit une bijection entre les idéaux de A contenant I et les idéaux de A / I. Cette bijection respecte le caractère premier des idéaux.
Soit I idéal d'un anneau commutatif A. La projection canonique met en bijection l'ensemble des idéaux premiers de A contenant I et l'ensemble des idéaux premiers de A / I.
Les idéaux contenus dans I peuvent pour leur part être isolés des autres par le procédé de localisation. On a alors l'énoncé suivant :
Soit I idéal premier d'un anneau commutatif A. La localisation met en bijection l'ensemble des idéaux premiers de A contenus dans I et l'ensemble des idéaux premiers de l'anneau localisé AI.
Dimension de Krull
La structure ordonnée par l'inclusion de l'ensemble des idéaux premiers est à la source d'une des définitions possibles de la dimension d'un anneau, cohérente avec l'intuition géométrique pour les anneaux qui interviennent en géométrie algébrique. La dimension de Krull d'un anneau commutatif A est définie comme le plus grand n pour lequel il existe une chaîne strictement croissante d'idéaux premiers de A de la forme :
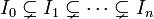
Topologie sur le spectre et spectre maximal
L'ensemble des idéaux premiers d'un anneau commutatif A est appelé le spectre premier de A. Il est possible de le munir d'une topologie, dite de Zariski, qui généralise la topologie de Zariski d'un ensemble algébrique. Une fois cette topologie définie, l'espace topologique Spec(A) peut être équipé d'un faisceau d'anneaux, localisés de A. L'objet est alors à la base de la définition des schémas, qui généralisent les variétés algébriques.
Si le spectre premier, parce que sa construction est fonctorielle, est particulièrement adapté à la géométrie algébrique, le spectre maximal, ensemble des idéaux maximaux, est souvent sollicité en analyse fonctionnelle, particulièrement en théorie des algèbres de Banach commutatives unitaires. Il peut être muni d'une topologie séparée. La transformation de Gelfand (en) permet alors, lorsqu'elle est injective, d'interpréter les éléments de l'algèbre de Banach comme des fonctions sur le spectre de l'algèbre.
Aspect historique
La théorie des idéaux est relativement récente puisqu'elle fut créée par Richard Dedekind vers la fin du XIX siècle. À cette époque, une partie de la communauté mathématique s'intéressait aux nombres algébriques et plus particulièrement aux entiers algébriques.
La question était de savoir si les entiers algébriques se comportent comme les entiers relatifs, en particulier la décomposition en facteurs premiers de manière unique. Il semblait bien, dès le début du XIX siècle, que cela n'était pas toujours le cas : 6 par exemple pouvant se décomposer dans l'anneau Z[i√5] sous la forme 2 × 3 ou sous la forme (1 + i√5)(1 – i√5).
Ernst Kummer pressent alors que cela va dépendre des nombres en question et invente la notion de nombres complexes idéaux.
L'idée est de rendre unique la décomposition en facteurs premiers en ajoutant artificiellement d'autres nombres (de la même manière qu'on ajoute i aux nombres réels tel que 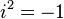 afin de disposer de nombres aux carrés négatifs). Dans l'exemple ci-dessus, on va « inventer » quatre nombres « idéaux » a, b, c et d tels que :
afin de disposer de nombres aux carrés négatifs). Dans l'exemple ci-dessus, on va « inventer » quatre nombres « idéaux » a, b, c et d tels que :
-
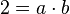
-
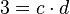
-
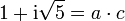
-
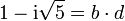
Ainsi, 6 se décomposera alors de manière unique en :
-
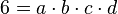
C'est Dedekind qui reprend en 1871 la notion de nombre idéal (en) de Kummer et qui crée la notion d'idéal dans un anneau. Il s'intéresse principalement aux anneaux d'entiers algébriques, qui sont intègres. C'est dans ce domaine que se trouvent les résultats les plus intéressants sur les idéaux. Il crée sur l'ensemble des idéaux d'un anneau intègre des opérations semblables à l'addition et la multiplication dans les entiers relatifs.
La théorie des idéaux a permis une avancée significative dans l'algèbre générale, mais aussi dans l'étude des courbes algébriques (géométrie algébrique).
Quelques notions homonymes
Dans d'autres contextes mathématiques, divers objets sont aussi appelés idéaux, chacun apparenté ou analogue en un certain sens aux idéaux d'anneaux traités dans cet article :
En algèbre commutative, les idéaux fractionnaires sont de proches parents des idéaux et interviennent notamment dans l'étude des anneaux de Dedekind ;
On peut définir de façon très analogue un idéal dans une algèbre, même non associative. On parle notamment d'idéal d'une algèbre de Lie.
Dans un treillis, il existe un concept d'idéal du treillis, dont la définition présente une grande analogie formelle avec celle d'un idéal d'un anneau.
Sources
1 2 3 4 Nicolas Bourbaki, Algèbre - Chapitres 1 à 3, Hermann, 1970, p. 98-99
↑ C'est par exemple le choix fait dans (en) Carl Faith, Algebra. I, rings, modules and categories, Berlin, Springer-Verlag, 1973 (ISBN 978-0-387-05551-0), p. 123
↑ (en) Louis Rowen, Ring theory, vol. 1, Boston, Academic Press, 1988, 1 éd. (ISBN 978-0-12-599841-3, LCCN 87014536), p. 21. Si les idéaux bilatères sont relativement peu présents dans l'arsenal théorique de l'algèbre non commutative, ils n'en demeurent pas moins essentiels comme mode de construction d'exemples par passage au quotient ; voir en ce sens plusieurs des exemples au chapitre I de (en) T. Y. Lam, A First Course in Noncommutative Rings, New York, Springer-Verlag, coll. « GTM » (n 131), 1991, 1 éd. (ISBN 978-0-387-97523-8, LCCN 91006893, lire en ligne).
↑ L. Rowen, op. cit., p. 16
↑ Roger Godement, Cours d'Algèbre, Hermann, 1966, 2 éd., p. 148 pour un exemple d'ouvrage qui définit les idéaux bilatères sans référence préalable aux idéaux à gauche et à droite.
↑ Cet énoncé est utilisé comme définition d'un idéal bilatère par Carl Faith, op. cit., p. 113
↑ Annette Paugam, Agrégation de mathématiques. Questions délicates en algèbre et en géométrie, Dunod (ISBN 978-2-10-051378-9), p. 92 et 156-158 (y compris pour l'exemple des idéaux maximaux)
1 2 Louis Rowen, op. cit., p. 7-8
1 2 David Dummit et Richard Foote, Abstract algebra, Prentice-Hall, 1991, p. 250-251
↑ David Dummit et Richard Foote, op. cit., p. 250 pour les idéaux bilatères. Pour les idéaux à gauche ou à droite, les sources consultées se bornent à renvoyer implicitement à la notion de sous-module de type fini.
↑ (en) J.C. McConnell et J.C. Robson, Noncommutative Noetherian Rings, Providence, AMS, coll. « Graduate Studies in Mathematics » (n 30), 2001 (ISBN 978-0-8218-2169-5, LCCN 00034990, lire en ligne), p. 2 (pour l'ensemble de la section jusqu'à cette note).
↑ Lam 1991, p. 21. Lam qualifie le théorème de « hautement non trivial » ("highly non trivial").
↑ Grillet fait remarquer qu'il y a un heurt de notations, l'ensemble de ces produits (qui n'est pas un sous-groupe en général) pouvant en principe être lui aussi noté IJ. Cette confusion n'est pas gênante en pratique, cet ensemble de produits étant rarement évoqué en tant que tel.
1 2 Serge Lang, Algèbre [détail des éditions], p. 99-100 dans l'édition Dunod
↑ La définition est formellement la même si on note additivement l'opération Sup et multiplicativement l'opération Inf du treillis, cf. (en) Pierre-Antoine Grillet, Abstract Algebra, New York, Springer-Verlag, 2007, 2 éd. (ISBN 978-0-387-71567-4, LCCN 2007928732), p. 552
En outre, la section d'histoire a été écrite en utilisant Jacques Bouveresse, Jean Itard et Émile Sallé, Histoire des mathématiques[détail des éditions].
Portail de l’algèbre

 词典释义:
词典释义:
 :
: 世界
世界
 , 完善
, 完善 , 圆满
, 圆满 ; <口>十全十美:
; <口>十全十美: 解决方法
解决方法 典范
典范 满足; 理想:
满足; 理想: 是…
是… 女人
女人 解决办法
解决办法 ,完善
,完善 ;
; ,享有特殊利益
,享有特殊利益 ;
; ,必要
,必要 ;
; ,恩惠
,恩惠 ;
; ,完善
,完善 ,完美
,完美 ;
; ,最
,最 宜
宜 ,最令人满意
,最令人满意 ,最有利
,最有利 ;
; , 无法回避
, 无法回避 ;
; 合
合 ,
,

 ,
,
 ;
;
 ,
, 本
本 ;
; ,充足
,充足 ,足够
,足够 ;
; , 完美
, 完美
 ;
;
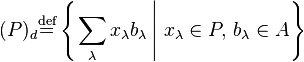 ;
;
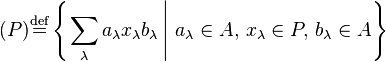 .
.
 , la somme de la famille, notée
, la somme de la famille, notée 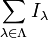 est l'ensemble des sommes
est l'ensemble des sommes 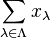 ne contenant qu'un nombre fini de termes et où
ne contenant qu'un nombre fini de termes et où 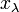 varie dans
varie dans 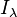 . Cet ensemble est lui aussi un idéal du même type, et c'est aussi l'idéal de ce type engendré par la réunion des
. Cet ensemble est lui aussi un idéal du même type, et c'est aussi l'idéal de ce type engendré par la réunion des  .
.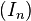 constante à partir d'un certain rang (c'est-à-dire pour laquelle il existe un n tel que
constante à partir d'un certain rang (c'est-à-dire pour laquelle il existe un n tel que 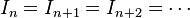 ).
).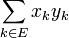 où E est un ensemble fini,
où E est un ensemble fini, 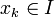 et
et 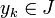 .
.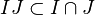 mais l'inclusion peut être stricte comme le montre l'exemple précédent.
mais l'inclusion peut être stricte comme le montre l'exemple précédent. défini par
défini par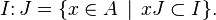
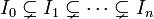
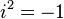 afin de disposer de nombres aux carrés négatifs). Dans l'exemple ci-dessus, on va « inventer » quatre nombres « idéaux » a, b, c et d tels que
afin de disposer de nombres aux carrés négatifs). Dans l'exemple ci-dessus, on va « inventer » quatre nombres « idéaux » a, b, c et d tels que