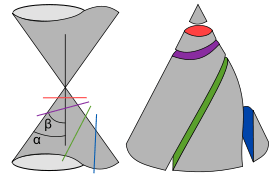
Différentes coniques obtenues comme intersection d'un cône de révolution et d'un plan selon l'inclinaison de celui-ci: cercle (rouge), ellipse (violet), parabole (vert), partie inférieure d'une hyperbole (bleue).
En mathématiques, et plus précisément en géométrie, les coniques constituent une famille très utilisée de courbes planes algébriques. Elles tirent leur nom du fait qu'elles ont d'abord été définies comme l'intersection d'un cône de révolution avec un plan. Parmi les coniques non dégénérées, on compte la parabole, l'ellipse et l'hyperbole.
Les coniques peuvent être définies de plusieurs façons différentes globalement semblables pour les courbes de base : comme intersection de cône, par foyer, directrice, et excentricité ou par une propriété bifocale.
Leur équation générale les relie à l'étude des formes quadratiques.
Les intersections de cône par un plan pouvant être vues comme des projections coniques d'un cercle sur un plan, l'étude des coniques en géométrie projective permet d'obtenir des résultats puissants et donne lieu à l'étude des coniques projectives.
Définitions métriques
Intersection d'un cône par un plan
On obtient une conique en prenant l'intersection d'un plan avec un cône dont la courbe directrice est un cercle. On peut, dans l'étude, se limiter à l'intersection d'un plan avec un cône de révolution.
Selon les positions relatives du plan de coupe et du cône de révolution, on obtient différents types de coniques :
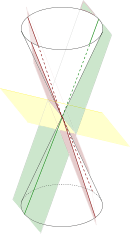
Exemples de coniques dégénérée
Des coniques propres, quand le plan de coupe ne passe pas par le sommet du cône. On distingue trois sortes de coniques propres en fonction de l'angle d’inclinaison du plan de coupe avec l’axe du cône : si cet angle d'inclinaison est inférieur à l'angle d'ouverture (angle formé par l'axe du cône et une génératrice), l'intersection est une hyperbole ; si cet angle d'inclinaison est égal à l'angle d'ouverture du cône, l'intersection est une parabole ; si cet angle d'inclinaison est supérieur à l'angle d'ouverture du cône, l'intersection est une ellipse; dans le cas maximal où l'angle d'inclinaison du plan de coupe est droit, cette ellipse est même un cercle.
si cet angle d'inclinaison est inférieur à l'angle d'ouverture (angle formé par l'axe du cône et une génératrice), l'intersection est une hyperbole ;
si cet angle d'inclinaison est égal à l'angle d'ouverture du cône, l'intersection est une parabole ;
si cet angle d'inclinaison est supérieur à l'angle d'ouverture du cône, l'intersection est une ellipse;
dans le cas maximal où l'angle d'inclinaison du plan de coupe est droit, cette ellipse est même un cercle.
Des coniques dégénérées (en), quand le plan contient le sommet du cône. Là encore, on distingue trois sortes de coniques dégénérées en fonction de l'angle d’inclinaison du plan de coupe avec l’axe du cône : si cet angle d'inclinaison est inférieur à l'angle d'ouverture du cône, l'intersection est réduite à un couple de droites sécantes (deux génératrices du cône). si cet angle d'inclinaison est égal à l'angle d'ouverture du cône, l'intersection est réduite à une seule droite (une des génératrices du cône là où le plan de coupe et le cône sont tangents) ; si cet angle d'inclinaison est supérieur à l'angle d'ouverture du cône, l'intersection est réduite à un seul point (le sommet du cône).
si cet angle d'inclinaison est inférieur à l'angle d'ouverture du cône, l'intersection est réduite à un couple de droites sécantes (deux génératrices du cône).
si cet angle d'inclinaison est égal à l'angle d'ouverture du cône, l'intersection est réduite à une seule droite (une des génératrices du cône là où le plan de coupe et le cône sont tangents) ;
si cet angle d'inclinaison est supérieur à l'angle d'ouverture du cône, l'intersection est réduite à un seul point (le sommet du cône).
Définition par foyer, directrice et excentricité
La définition par foyer et directrice des coniques est encore appelée définition monofocale de ces coniques.
Définition
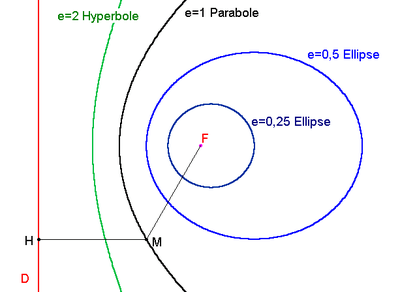
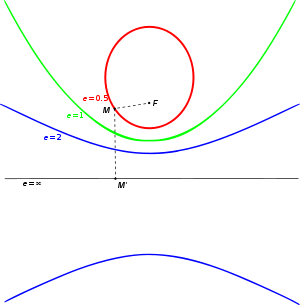
Quatre coniques ayant même foyer et même directrice
Dans un plan (p), on considère une droite (D) et un point F non situé sur (D). Soit  un réel strictement positif.
un réel strictement positif.
On appelle conique de droite directrice (D), de foyer F et d'excentricité  l'ensemble des points M du plan (p) vérifiant :
l'ensemble des points M du plan (p) vérifiant :
-
![[1]\qquad \mathrm{d}(\mathrm{M}, \mathrm{F}) = e \mathrm{d}(\mathrm{M},(\mathrm{D}))](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/51fb7f7a6002bf390ad18ad81fb13a33.png)
où
mesure la distance du point M au point F
et
mesure la distance du point M à la droite (D)
Le paramètre e définit la forme de la conique, c'est-à-dire que deux coniques ayant même excentricité sont image l'une de l'autre par une similitude.
si e < 1, on obtient une courbe fermée et bornée (ellipse);
si e=1, on obtient une courbe ouverte et infinie (parabole);
si e > 1 on obtient une courbe possédant deux branches symétriques par rapport au point d'intersection de leurs asymptotes communes (hyperbole)
Toutes ces courbes possèdent comme axe de symétrie la droite passant par F et perpendiculaire à (D) appelé axe principal de la conique.
Équations cartésiennes
On note K le projeté orthogonal du point F sur la droite (D) et h la distance de K à F (le produit p = eh s'appelle le paramètre de la conique depuis Pierre Hérigone).
Pour tout point 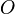 de l'axe principal, on peut construire le repère orthonormal
de l'axe principal, on peut construire le repère orthonormal 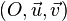 où
où 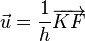 dans lequel
dans lequel 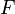 a pour abscisse
a pour abscisse  .
.
Pour un point M de coordonnées 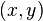 on peut exprimer les distances précédentes à l'aide des deux formules suivantes :
on peut exprimer les distances précédentes à l'aide des deux formules suivantes : ![[2] \qquad \mathrm{d}(\mathrm{M}, \mathrm{F}) = \sqrt{ (x-\alpha)^2 + (y-0)^2 }](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/29fc85239e21112f77d3dc512421c4f3.png)
![[3] \qquad \mathrm{d}(\mathrm{M}, (\mathrm{D})) = \sqrt{ (x-\alpha + h)^2 }](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/70a073a5a2093c70cf6b98cb2530b9a7.png) ce qui implique en élevant [1] au carré et en utilisant [2] et [3] :
ce qui implique en élevant [1] au carré et en utilisant [2] et [3] : ![[4] \qquad (x-\alpha)^2 + y^2 = e^{2}(x - \alpha + h)^2](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/f173d922ba81efbe79fbfa853dddad8f.png) soit après réduction :
soit après réduction : ![[5] \qquad x^2(1-e^2) + y^2 =2Bx +C](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/47be4880bc714891258936030523b4f4.png) où
où 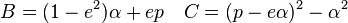
Un choix judicieux de O permet de simplifier cette équation
Centre du repère au sommet de la conique
En prenant 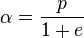 , le coefficient C s'annule et
, le coefficient C s'annule et 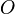 est un point de la conique appelé sommet. L'équation s'écrit:
est un point de la conique appelé sommet. L'équation s'écrit: 
En particulier, dans le cas où e =1, on retrouve l'équation caractéristique de la parabole:
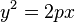
Centre du repère au centre de la conique
Dans le cas où e est différent de 1, pour 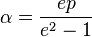 , le coefficient B s'annule et le point
, le coefficient B s'annule et le point  est centre de symétrie de la conique. L'équation s'écrit :
est centre de symétrie de la conique. L'équation s'écrit : 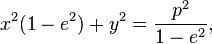 dans laquelle on retrouve en posant
dans laquelle on retrouve en posant 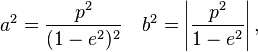 les équations caractéristiques suivantes :
les équations caractéristiques suivantes :
pour e < 1 - cas de l'ellipse
pour e > 1 - cas de l'hyperbole
Cas particulier du cercle
Dans les équations précédentes, on trouve l'équation d'un cercle de rayon r dans le cas où e = 0 et p=r. On considère alors le cercle comme un cas particulier d'ellipse d'excentricité nulle, dont le foyer est situé au centre du cercle et dont la directrice est envoyée à l'infini.
Équation polaire
Dans le repère d'origine F et de direction 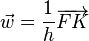 , une telle conique a pour équation polaire :
, une telle conique a pour équation polaire : 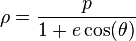
Réciproquement, toute courbe dont l'équation polaire dans un repère 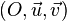 est :
est : 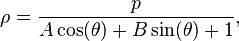 où p est un réel non nul, et (A,B) un couple de réels différent de (0,0), est une conique de foyer O, d'excentricité
où p est un réel non nul, et (A,B) un couple de réels différent de (0,0), est une conique de foyer O, d'excentricité 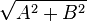 et d'axe la droite d'équation Ay=Bx.
et d'axe la droite d'équation Ay=Bx.
Cette forme d'équation polaire est utile dans l'étude de la trajectoire des planètes.
Définition bifocale
L'ellipse peut être définie comme le lieu des points dont la somme des distances à deux points fixes, appelés foyers de l'ellipse, est constante et égale à une valeur fixée. Cette définition reste valable dans le cas du cercle, pour lequel les foyers sont confondus.
L'hyperbole peut être définie comme le lieu des points dont la valeur absolue de la différence des distances à deux points fixes, appelés foyers de l'hyperbole, est constante et égale à une valeur fixée.
La parabole n'a pas de définition bifocale.
Cette propriété bifocale correspond à une autre définition d'une conique par un point et une courbe directrice : l’ensemble des centres des cercles passant par un point fixe F et tangent à, soit un cercle fixe (C) ne passant pas par F, soit une droite fixe (D) ne contenant pas F, est une conique de foyer F et de courbe directrice (C) ou (D).
Si F est intérieur à (C), la courbe est une ellipse ; si F est extérieur à (C) la courbe est une hyperbole ; si la directrice est une droite, la courbe est une parabole.
En notant F' le centre du cercle (C) et 2a son rayon (a > 0), on obtient en effet :
dans le cas de l'ellipse, le cercle centré en M est tangent intérieurement à (C), et le point M vérifie MF + MF' = 2a ;
dans le cas de l'hyperbole, le cercle (C) est tangent au cercle centré en M, soit intérieurement, et le point M vérifie MF - MF' = 2a, soit extérieurement, et le point M vérifie MF' - MF = 2a. On regroupe les deux cas par la condition |MF - MF'| = 2a.
Les points F et F' sont les foyers de la conique.
Quant à la parabole, on retrouve, pour le cercle centré en M passant par F et tangent à (D), l'égalité MF= d(M,(D)).
Liens entre les définitions
Définition monofocale et définition bifocale
Les paraboles admettent un et un seul couple foyer/directrice au sens de la définition monofocale, et l'excentricité correspondante vaut 1.
Ellipses et hyperboles admettent exactement deux couples foyer/directrice au sens de la définition monofocale, et ceux-ci correspondent à une même valeur de l'excentricité. Ils sont symétriques par rapport au centre de l'ellipse ou au point d'intersection des asymptotes de l'hyperbole. Ces foyers sont les points intervenant dans la définition bifocale.
Définition géométrique, foyers et directrices
Les foyers et les directrices des coniques peuvent être déterminés géométriquement dans le cadre de la définition des coniques comme intersection d'un cône et d'un plan ne passant pas par le centre de celui-ci.
Il existe, selon l'orientation du plan par rapport à l'axe du cône, une (cas des paraboles) ou deux (cas des ellipses et des hyperboles) sphères tangentes à la fois au plan et au cône; ce sont des sphères centrées sur l'axe, situées dans un même demi-cône (cas des ellipses) ou dans des demi-cônes opposés (cas des hyperboles).
Chacune de ces sphères définit l'un des foyers de la conique (c'est le point de tangence de la sphère et du plan) ainsi que la droite directrice associée (c'est l'intersection du plan de la conique et du plan contenant le cercle de tangence de la sphère et du cône) ; c'est le théorème de Dandelin.
Définition algébrique
Dans un espace affine muni d'un repère, on appelle conique tout ensemble de points M(x, y) vérifiant une égalité de la forme
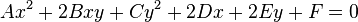
où A, B, C, D, E, F sont des constantes telles que (A,B,C) ≠ (0,0,0).
L'ensemble des coniques est stable par transformation affine ou par changement de repère.
Équation réduite en géométrie euclidienne
Une conique étant donnée, avec son équation dans un repère quelconque, on cherche à déterminer un repère orthonormal dans lequel l'équation de la conique serait aussi simple que possible. On se place d'emblée dans le cas où l'équation est donnée dans un repère orthonormal, si ce n'est pas le cas, on peut s'y ramener par changement de base. On peut également éliminer le terme en xy en changeant de base par rotation.
En effet, les équations de changement de base, pour une rotation d'angle θ, sont : 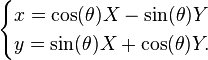
Le coefficient devant XY s'écrit alors : 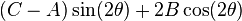 et si B est non nul, ce coefficient s'annule lorsque 2θ est un argument de C - A - 2Bi
et si B est non nul, ce coefficient s'annule lorsque 2θ est un argument de C - A - 2Bi
On suppose désormais que la conique a pour équation :

et l'on distingue trois éventualités.
Si A1C1 > 0
Un changement d'origine en prenant O1(− D1/A1,− E1/C1) permet d'éliminer les termes en x et y. La conique a pour équation dans ce nouveau repère : 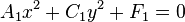 Trois cas se présentent alors :
Trois cas se présentent alors :
si F1 est de signe opposé à A1 et C1, en posant a = − F1/A1 et b = − F1/C1, on obtient l'équation réduite d'une ellipse;
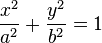
si F1 est nul, la conique est réduite à un point: O1;
si F1 est de même signe que A1 et C1, la conique est vide.
Si A1C1 < 0
Le même changement de repère conduit à l'équation : 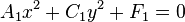 et l'on peut même, en permutant éventuellement les vecteurs de la base, supposer que C1F1 ≥ 0. Deux cas se présentent alors :
et l'on peut même, en permutant éventuellement les vecteurs de la base, supposer que C1F1 ≥ 0. Deux cas se présentent alors :
si F1 est non nul, en posant a = − F1/A1 et b = F1/C1, on obtient l'équation réduite d'une hyperbole;
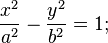
si F1 est nul, en posant a = |1/A1| et b = | 1/C1|, la conique est la réunion de deux droites sécantes d'équations : bx ± ay = 0.
Si A1C1 = 0
On peut, en permutant éventuellement les vecteurs de la base, supposer que A1 est nul et C1 non nul. Un changement d'origine en prenant O1(0,− E1/C1) conduit à l'équation 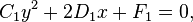 et deux cas se présentent :
et deux cas se présentent :
Si D1 est non nul, le changement d'origine en prenant O2(− F1/(2D1),0) permet d'éliminer le terme constant. Ensuite, en posant p = − D1/C1, on obtient l'équation réduite d'une parabole
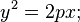
Si D1 est nul, l'équation se réduit à
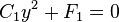
si F1 est de signe opposé à C1, en posant p = − F1/C1 la conique est la réunion de deux droites parallèles d'équations y = ± p
si F1 est nul, la conique se réduit à une droite d'équation y = 0
si F1 est de même signe que C1, la conique est vide
Ces équations réduites permettent de mettre en évidence les orbites des coniques pour les isométries : toutes les coniques d'une même classe avec les mêmes paramètres sont isométriques.
Classification affine
On se place dans le cadre d'un plan affine réel muni d'un repère et on considère l'ensemble des fonctions f définies pour tout point M(x, y) par 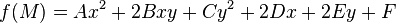 où A, B, C, D, E, F sont des constantes réelles telles que (A,B,C) ≠ (0,0,0).
où A, B, C, D, E, F sont des constantes réelles telles que (A,B,C) ≠ (0,0,0).
On note Cf la conique d'équation f(M) = 0. La question qui se pose est de savoir quel est l'effet des transformations affines sur la conique Cf, plus exactement de déterminer son orbite pour les transformations affines. Pour deux coniques Cf1 et Cf2, on observe que s'il existe une transformation affine et un réel λ non nul tels que f1 o φ = λf2, alors φ ( Cf2) = Cf1. On dit alors que f1 et f2 sont affinement équivalentes. Le but de la classification affine est de ranger les fonctions f en classe d'équivalence.
On définit pour cela
On obtient les écritures matricielles de f suivantes 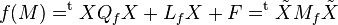
On démontre ensuite que f1 et f2 sont affinement équivalentes si et seulement si Qf1 et Qf2 ont même signature (à l'ordre près) ainsi que Mf1 et Mf2. De plus la signature de Qf (à l'ordre près) caractérise le signe de son déterminant AC -B. On obtient alors une classification des coniques en fonction des signatures de ces deux matrices:
| Signature de Qf |
signe de AC -B |
Signature de Mf |
Det(Mf) |
Équation type |
Classe de conique |
| (2,0) |
positif |
(3,0) |
non nul |
X + Y + 1 = 0 |
Vide |
| (2,1) |
non nul |
X + Y - 1 = 0 |
Ellipse |
| (2,0) |
nul |
X + Y = 0 |
Un point |
| (1,1) |
négatif |
(1,2) |
non nul |
X - Y - 1 = 0 |
Hyperbole |
| (1,1) |
nul |
X - Y = 0 |
Deux droites sécantes |
| (1,0) |
nul |
(2,1) |
non nul |
X -Y = 0 |
Parabole |
| (2,0) |
nul |
X +1 = 0 |
Vide |
| (1,1) |
nul |
X - 1 = 0 |
Deux droites parallèles |
| (1,0) |
nul |
X= 0 |
Une droite |
Quand le déterminant de Mf est nul, on dit que la conique est dégénérée.
Géométrie projective
En géométrie projective, les coniques sont encore les courbes planes algébriques du second degré, c'est-à-dire les courbes planes caractérisées dans un certain repère projectif par une équation polynomiale homogène de degré 2. Une telle équation a pour forme (voir coordonnées homogènes)
-

avec A, B et C non tous nuls.
Les coordonnées (X, Y,Z) d'un point dans un repère de l'espace projectif ne sont pas toutes nulles, et deux triplets de coordonnées proportionnelles définissent le même point. On travaille plus précisément dans le plan projectif réel P(E), où E est l'espace vectoriel réel de dimension 3. Une conique projective réelle est une courbe qui possède une équation polynomiale homogène du second degré dans un repère projectif de P(E).
Même pour les coniques réelles (les coefficients A, B, C, D, E, F ci-dessus sont réels), il peut être utile de considérer le complexifié P(EC) de P(E), qui est le plan projectif complexe. Un repère de P(E) est aussi un repère de P(EC), les coordonnées étant complexes. Les points réels sont ceux de P(E), les points imaginaires ceux de P(EC) qui ne sont pas dans P(E). Les points imaginaires sont ceux qui ont au moins une coordonnée non réelle dans un repère de P(E) (ceci ne dépend pas du repère). Sauf précision, les points de la conique sont les points réels qui satisfont l'équation, mais on peut parler des points imaginaires d'une conique réelle.
Les coordonnées homogènes sont les coordonnées dans la base de E déterminée par le repère projectif choisi. On voit alors qu'une conique de P(E) est définie par une forme quadratique sur E. Plus précisément la conique (Cq) de P(E) associée à une forme quadratique q de E est l'ensemble des points de P(E) déterminés par des vecteurs non nuls u de E tels que q(u)=0. Deux formes quadratiques proportionnelles définissent la même conique.
Une conique est dite propre si elle est associée à une forme quadratique non dégénérée, dégénérée sinon. Une forme quadratique dégénérée est soit le carré d'une forme linéaire, soit la somme ou la différence de carrés de formes linéaires. Elle se factorise donc toujours comme produit de deux formes linéaires (éventuellement complexes). Les noyaux de ses formes linéaires sont des plans qui définissent des droites projectives (éventuellement complexes). Une conique dégénérée réelle non vide (sur l'espace réel) est donc soit une droite, soit la réunion de deux droites (éventuellement complexes).
L'image d'une conique par une homographie est encore une conique, puisque celle-ci correspond à une transformation linéaire f sur E, si la conique est associée à la forme quadratique q, l'image de celle-ci est associée à la forme quadratique q o f.
Classification projective des coniques réelles
La classification projective des coniques est la classification à homographie près : deux coniques sont dans la même classe si l'une est image de l'autre par une homographie. Elle se déduit donc de la classification des formes quadratiques, sachant que deux coniques proportionnelles (opposées en particulier) définissent la même conique. La classification projective des coniques réelles s'obtient alors directement à partir de celle des formes quadratiques réelles donnée par la loi d'inertie de Sylvester. Autrement dit, l'orbite d'une conique réelle sous l'action du groupe projectif linéaire (en) PGL(3,R) est caractérisée par la signature de la forme quadratique.
Comme deux formes quadratiques opposées sont associées à la même conique, on peut toujours supposer que le premier terme de la signature est supérieur ou égal au second.
Par diagonalisation des formes quadratiques, par exemple par réduction de Gauss, on obtient une écriture de celle-ci comme somme et/ou différence de carrés qui est déterminée par la signature. La conique est alors l'image par transformation projective d'une conique de l'équation réduite indiquée dans le même repère, ou, de façon équivalente, il existe un repère dans lequel l'équation de la conique est l'équation indiquée.
| Forme quadratique |
Conique |
| rang |
Signature |
Équation type |
Classe |
| 3 |
(3,0) |
X + Y + Z = 0 |
Conique propre imaginaire, vide sur le plan projectif réel |
| 3 |
(2,1) |
X + Y - Z = 0 |
Conique propre réelle |
| 2 |
(2,0) |
X + Y = 0 |
Conique dégénérée en un seul point réel (deux droites sécantes complexes) |
| 2 |
(1,1) |
X - Y = 0 |
Conique dégénérée en deux droites sécantes (réelles) |
| 1 |
(1,0) |
X = 0 |
Conique dégénérée en une droite double (réelle) |
| Le rang de la forme quadratique est précisé mais se déduit de la signature ; on parle également de rang pour la conique associée. |
En particulier, il n'y a à homographie près qu'une seule conique projective réelle non dégénérée non vide, celle qui a pour équation dans un certain repère projectif X+Y-Z=0 (signature (2,1) ou (1,2)). Cette équation est celle d'un cône à base elliptique de sommet l'origine dans l'espace vectoriel E.
Coniques projectives et affines
Un plan affine peut toujours être plongé dans un espace vectoriel E de dimension 3, comme plan affine ne passant pas par l'origine. Un repère de E peut être choisi de façon que le plan affine soit identifié au plan affine d'équation Z = 1 dans ce repère. Ce plan affine apparait alors également comme la partie du plan projectif P(E) formée des points de coordonnées homogènes (X:Y:1), donc par homogénéité ceux de coordonnées (X:Y: Z) avec Z ≠ 0. Les points de coordonnées (X;Y:0) forment alors une droite projective, qui est la droite à l'infini associée au plan affine.
La restriction de la conique projective d'équation
-

au plan affine Z = 1, a pour équation, en choisissant le repère affine déduit du repère projectif
-
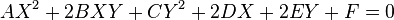
et on a bien l'équation d'une conique affine, et par l'opération inverse, en homogénéisant l'équation de la conique affine, celle-ci apparaît comme la restriction au plan affine d'une conique projective.
L'intersection de la conique projective avec la droite à l'infini associée au plan affine a pour équation
-
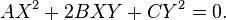
Le trinôme AX + 2BXY + CY est la forme quadratique à l'infini de la conique affine. Le nombre de solutions de l'équation à homogénéïté près est le nombre de point à l'infini de la conique. Celui-ci est 0, 1, ou 2, suivant le signe de B -AC, discriminant (réduit) de l'équation (en Y/X ou X/Y suivant que l'on cherche des solutions telles que X est non nul ou Y est non nul).
On retrouve alors la classification affine à partir de la classification projective et du nombre de points à l'infini : les critères sont les mêmes, signature de la forme quadratique donnée par l'équation homogénéisée, le discriminant est l'opposé du déterminant de la forme quadratique à l'infini. En particulier une ellipse (B -AC < 0) n'a pas de point à l'infini, une parabole (B -AC = 0) a un seul point double à l'infini, c'est-à-dire qu'elle est tangente à la droite à l'infini, une hyperbole (B -AC > 0) a deux points à l'infini.
Cas barycentrique
En géométrie analytique barycentrique, les coniques sont toujours les courbes planes algébriques du second ordre, c'est-à-dire les courbes planes dont les points ont des coordonnées barycentriques λ, μ et ν qui vérifient une équation polynomiale homogène du second degré de la forme :
-
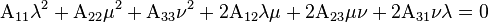
On peut identifier cette équation à la précédente, en posant :
-
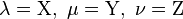
On obtient alors, à un coefficient multiplicatif près :
-
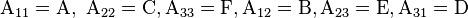
Propriétés d'incidence
Intersection d'une conique avec une droite
Conique passant par cinq points
Histoire
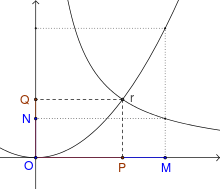
Problème de Ménechme: OM et ON étant donnés, il faut placer OP et OQ tels que OM/OP=OP/OQ=OQ/ON. Cette série d'égalités est équivalente à OP² = OM.OQ (1) et OP.OQ = OM.ON (2). Ces deux conditions placent le point r, quatrième point du rectangle POQr, à l'intersection d'une parabole (1) et d'une hyperbole (2)
L'étude des coniques remonte, en Grèce, au moins jusqu'au IV siècle av. J.-C. quand Ménechme recherchant une double moyenne proportionnelle entre deux segments, la trouve comme l'intersection de deux courbes, une parabole et une hyperbole. Ménechme ne donne pas de nom à ses courbes. Elles furent également étudiées par Euclide et Aristée. Pour eux, un cône est obtenu comme rotation d'un triangle (ABC) rectangle en B autour d'un côté de l'angle droit AB, l'hypoténuse est appelée génératrice du cône. Le cône est dit rectangle si l'angle de sommet A est égal à 45°, acutangle (respectivement obtusangle) si l'angle de sommet A est inférieur (respectivement supérieur) à 45°. Pour Aristée, une conique est obtenue par intersection d'un cône avec un plan perpendiculaire à une génératrice. Si le cône est rectangle, la section (parabole) est appelée une section rectangle, si le cône est acutangle, la section (ellipse) est appelée section acutangle et si le cône est obtusangle, la section (hyperbole) est appelée section obtusangle du cône. Pour Apollonius de Perge, le cône est généré par un cercle, un point non situé dans le plan du cercle et une faisceau de droites passant par le point et s'appuyant sur le cercle (le cône n'est donc pas nécessairement droit). Il parle de surface conique et envisage les deux nappes du cône. Une conique est l'intersection d'un plan avec le cône, il est donc un des premiers à voir que l'hyperbole est formée de deux parties : une section et sa section opposée.
![Dans cette ellipse de centre O, les cordes MM', NN' et TT' sont ordonnées. Le segment [SS'] qui passe par le milieu de ces cordes est le diamètre associé aux cordes ordonnées. Les longueurs Sm, Sn et SO sont des abscisses et les longueurs mM, nN et OT sont des ordonnées. Le segment SP est le côté droit de l'ellipse associé à ce diamètre. Il est tel que SP=2OT²/OS.](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/EllipseDiametre.svg.png)
Dans cette ellipse de centre O, les cordes MM', NN' et TT' sont ordonnées. Le segment [SS'] qui passe par le milieu de ces cordes est le diamètre associé aux cordes ordonnées. Les longueurs Sm, Sn et SO sont des abscisses et les longueurs mM, nN et OT sont des ordonnées. Le segment SP est le côté droit de l'ellipse associé à ce diamètre. Il est tel que SP=2OT²/OS.
C'est également dans ses écrits que l'on trouve les termes d’abscisse et d’ordonnée : il remarque que dans une conique, des cordes parallèles ont des milieux alignés. La droite passant par ces milieux est appelée un diamètre, les segments parallèles sont appelés segment ordonnés et les segments découpés sur un diamètre par les ordonnées sont les abscisa (découpées).
Il caractérise également les coniques par une égalité d'aire : l'aire du carré s'appuyant sur une ordonnée est fonction de l'aire d'un rectangle s'appuyant sur l'abscisse. Il définit une longueur constante qu'il appelle le côté droit et qui portera plus tard le nom de paramètre (mesuré à côté) et s'en sert pour exprimer la relation d'aire :
dans une section parallèle à une génératrice du cône, l'aire du carré s'appuyant sur l'ordonnée est égale à l'aire du rectangle construit sur l'abscisse et de hauteur le côté droit. Il donne à cette courbe le nom de parabole (application simple);
dans une section traversant le cône, l'aire du carré s'appuyant sur l'ordonnée est inférieure à l'aire de ce rectangle. La courbe obtenue porte alors le nom d'ellipse (ajustement par défaut);
dans une section recoupant le cône dans l'autre nappe, l'aire du carré s'appuyant sur l'ordonnée est supérieure à l'aire de ce rectangle. La courbe porte alors le nom d'hyperbole (ajustement par excès).
Il précise par une construction la relation exacte entre l'aire du carré et l'aire d'un rectangle s'appuyant sur l'abscisse.
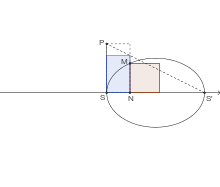
Égalité d'aire, dans une ellipse, entre le carré mené sur l'ordonnée et le rectangle bleu mené sur l'abscisse. Ce rectangle est plus petit que le rectangle de hauteur SP (paramètre de l'ellipse) d'où le nom de ellipse (ajustement par défaut) donné à la courbe par Apollonios
|
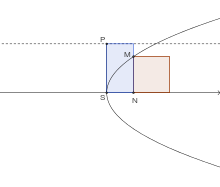
Égalité d'aire, dans une parabole, entre le carré mené sur l'ordonnée et le rectangle bleu mené sur l'abscisse. Ce rectangle est égal au rectangle de hauteur SP (paramètre de la parabole) d'où le nom de parabole (ajustement exact) donné à la courbe par Apollonios
|
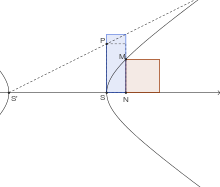
Égalité d'aire, dans une hyperbole, entre le carré mené sur l'ordonnée et le rectangle bleu mené sur l'abscisse. Ce rectangle est plus grand que le rectangle de hauteur SP (paramètre de l'hyperbole) d'où le nom de hyperbole (ajustement par excès) donné à la courbe par Apollonios
|
Cette propriété est illustrée par les équations de coniques dans un repère orthonormé (S, u, v) où S est un sommet de la conique et u le vecteur unitaire de l'axe principal orientant la demi-droite [S, u) vers l'intérieur de la conique : 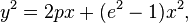
où p=eh dans le cas des coniques à foyer et directrice et où p = R dans le cas du cercle pour e=0. On voit en effet que l'aire du carré est égale à l'aire du rectangle dans le cas de la parabole (e=1), excède celle du rectangle dans le cas de l'hyperbole (e>1) et est en déficit par rapport à celle du rectangle dans le cas de l'ellipse (e < 1).
Il étudie également les asymptotes de l'hyperbole, les tangentes, les propriétés des foyers et les intersections de coniques
Apollonius accorde peu de place à la définition par foyer et directrice qui est plus spécialement étudiée par Pappus. C'est également Pappus qui montre comment déterminer les éléments remarquables d'une ellipse (centre et diamètre) lorsque 5 points sont connus. Les propriétés optiques des coniques sont utilisées dans les problèmes de réflexions notamment dans l'étude des miroirs ardents. Les quadratures (c'est-à-dire les calculs d'aire de surfaces délimitées par des coniques sont étudiées par Archimède qui entreprend la quadrature de la parabole, du cercle et montre la relation entre l'aire de l'ellipse et l'aire de son cercle directeur.
Les écrits d'Apollonius sont ensuite traduits en arabeet les coniques et leurs intersections sont exploitées pour théoriser la classification des équations de degré trois. Les mathématiciens de langue arabe élaborent des procédés mécaniques de tracés de coniques en continu (méthode du jardinier et sa variante pour l'hyperbole d'Ibn Sahl, compas parfait d'al Quhi). Ils exploitent les propriétés géométriques des coniques dans des problèmes optiques de réflexion et de réfraction.
Au XVII siècle, on assiste en Europe à un renouveau dans l'étude des coniques. La géométrie algébrique de René Descartes permet un traitement algébrique de ces courbes avec leur représentations paramétriques, travail entrepris pas Descartes, Pierre de Fermat, Isaac Newton qui démontre la relation entre les coniques et les trajectoires des planètes observée par Johannes Kepler, le marquis de l'Hospital et, au siècle suivant, par Leonhard Euler.
Mais le bond le plus important est lié aux avancées de la géométrie projective avec les travaux de Girard Desargues sur les involutions et les polaires de points par rapport à des coniques. Blaise Pascal démontre son théorème sur un hexagramme construit sur une conique. D'autres mathématiciens s'intéressent à ce sujet : Grégoire de Saint-Vincent qui entreprend le calcul d'aire sous l'hyperbole origine de la fonction logarithme, Jean de Witt s'intéresse aux tracés continus de coniques, Philippe de La Hire écrit une Nouvelle méthode en géométrie pour les sections et superficies coniques et Sectione Conicae faisant une recension des propriétés des coniques et présentant des démonstrations claires utilisant des propriétés projectives, des rapports harmoniques et des propriétés sur pôles et polaires.
Le XIX siècle voit l'avènement de la géométrie projective et de l'étude projective des coniques avec les écrits de Jean-Victor Poncelet, Michel Chasles qui énonce le théorème récemment découvert par Dandelin et Adolphe Quetelet, Jakob Steiner et Georg von Staudt.
L'étude des coniques est associée à celle des formes quadratiques avec les travaux d'Adrien-Marie Legendre, Carl Friedrich Gauss, Leonhard Euler, Augustin Louis Cauchy, Carl Jacobi, James J. Sylvester et Julius Plücker.

 词典释义:
词典释义:
 , 圆锥形
, 圆锥形


 曲线
曲线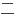
 曲线
曲线 ,圆筒形
,圆筒形 ;
; ,球形
,球形 ;
; ,隆起
,隆起 ,凸状
,凸状 ;
;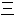
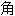 形
形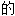 ,
,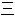
 ;
; ,矩形
,矩形 ;
; ,正方
,正方 ,四方
,四方 ;
; ,立方形
,立方形 ;
; ;
;
 ;
; ,管形
,管形 ,管状
,管状 ;
; ; 锥状
; 锥状 coniquef
coniquef
 曲线
曲线
 曲线
曲线 轴
轴 膜
膜 度铣刀
度铣刀 度铣刀
度铣刀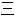 棱锥体
棱锥体

 un réel strictement positif.
un réel strictement positif.![[1]\qquad \mathrm{d}(\mathrm{M}, \mathrm{F}) = e \mathrm{d}(\mathrm{M},(\mathrm{D}))](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/51fb7f7a6002bf390ad18ad81fb13a33.png)

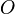 de l'axe principal, on peut construire le repère orthonormal
de l'axe principal, on peut construire le repère orthonormal 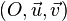 où
où 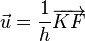 dans lequel
dans lequel 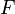 a pour abscisse
a pour abscisse 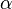 .
.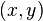 on peut exprimer les distances précédentes à l'aide des deux formules suivantes
on peut exprimer les distances précédentes à l'aide des deux formules suivantes![[2] \qquad \mathrm{d}(\mathrm{M}, \mathrm{F}) = \sqrt{ (x-\alpha)^2 + (y-0)^2 }](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/29fc85239e21112f77d3dc512421c4f3.png)
![[3] \qquad \mathrm{d}(\mathrm{M}, (\mathrm{D})) = \sqrt{ (x-\alpha + h)^2 }](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/70a073a5a2093c70cf6b98cb2530b9a7.png)
![[4] \qquad (x-\alpha)^2 + y^2 = e^{2}(x - \alpha + h)^2](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/f173d922ba81efbe79fbfa853dddad8f.png)
![[5] \qquad x^2(1-e^2) + y^2 =2Bx +C](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/47be4880bc714891258936030523b4f4.png)
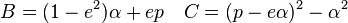
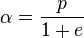 , le coefficient C s'annule et
, le coefficient C s'annule et 
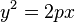
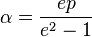 , le coefficient B s'annule et le point
, le coefficient B s'annule et le point 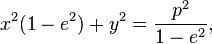
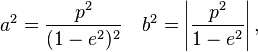
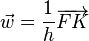 , une telle conique a pour équation polaire
, une telle conique a pour équation polaire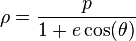
 est
est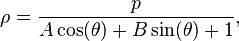
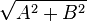 et d'axe la droite d'équation Ay=Bx.
et d'axe la droite d'équation Ay=Bx.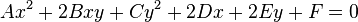
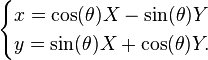
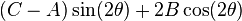

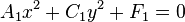
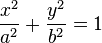
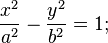
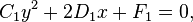
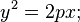
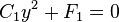
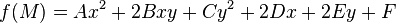
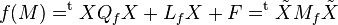

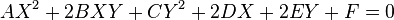
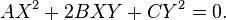
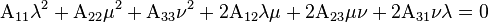
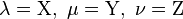
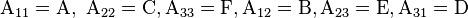

![Dans cette ellipse de centre O, les cordes MM', NN' et TT' sont ordonnées. Le segment [SS'] qui passe par le milieu de ces cordes est le diamètre associé aux cordes ordonnées. Les longueurs Sm, Sn et SO sont des abscisses et les longueurs mM, nN et OT sont des ordonnées. Le segment SP est le côté droit de l'ellipse associé à ce diamètre. Il est tel que SP=2OT²/OS.](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/EllipseDiametre.svg.png)



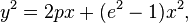
 ,这里的
,这里的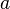 是椭圆的半长轴,或双曲线的半实轴。从中心到焦点的距离是
是椭圆的半长轴,或双曲线的半实轴。从中心到焦点的距离是 。
。 越接近于1,半短轴就越小。
越接近于1,半短轴就越小。