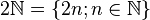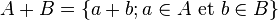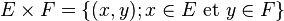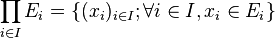Un ensemble désigne intuitivement une collection d’objets (les éléments de l'ensemble), « une multitude qui peut être comprise comme un tout » (au sens d'omnis).
Dans une approche axiomatique, la théorie des ensembles est une théorie de l'appartenance (un élément d'un ensemble est dit « appartenir » à cet ensemble). Le mot ensemble désigne alors un objet du domaine de cette théorie, dont les axiomes régissent les propriétés. La théorie des ensembles est utilisée pour fonder les mathématiques, et dans cette approche tout objet mathématique est in fine un ensemble.
Mais la notion d'ensemble est aussi une notion de base qui intervient dans à peu près tous les domaines des mathématiques.
Origines
La formulation en reviendrait au mathématicien Georg Cantor, qui énonçait : « Par ensemble, nous entendons toute collection M d'objets m de notre intuition ou de notre pensée, définis et distincts, ces objets étant appelés les éléments de M ». Ceci était particulièrement novateur, s'agissant d'ensembles éventuellement infinis (ce sont ces derniers qui intéressaient Cantor).
Ce qui est en jeu au premier chef dans la notion d'ensemble, c'est la relation d’appartenance : un élément appartient à un ensemble. Ce sont les propriétés de cette relation que Zermelo, puis d'autres, ont axiomatisées en théorie des ensembles. Il est assez remarquable que l'on puisse s'en contenter pour une théorie qui peut potentiellement formaliser les mathématiques. Mais ce n'était pas l'intention de Cantor, et il n'avait pas non plus axiomatisé sa théorie.
L'objet de cet article est de donner une approche intuitive de la notion d'ensemble, telle qu'elle est indiquée dans l'article théorie naïve des ensembles.
Ensembles, éléments et appartenance
Un ensemble peut être vu comme une sorte de sac virtuel entourant ses éléments, ce que modélisent bien les diagrammes de Venn. Souvent (ce n'est pas toujours possible), on essaye de le distinguer typographiquement de ses éléments, par exemple en utilisant une lettre latine majuscule, par exemple « E » ou « A », pour représenter l'ensemble, et des minuscules, telles que « x » ou « n », pour ses éléments.
Les éléments peuvent être de n’importe quelle nature : nombres, points géométriques, droites, fonctions, autres ensembles… On donne donc volontiers des exemples d'ensembles en dehors du monde mathématique. Par exemple : lundi est un élément de l’ensemble des jours de la semaine ; une bibliothèque est un ensemble de livres, etc.
Un même objet peut être élément de plusieurs ensembles : 4 est un élément de l'ensemble des nombres entiers, ainsi que de l’ensemble des nombres pairs (forcément entiers). Ces deux derniers ensembles sont infinis, ils ont une infinité d’éléments.
L'appartenance d'un élément, noté par exemple x, à un ensemble, noté par exemple A, s’écrit : x ∈ A.
Cet énoncé peut se lire :
« x appartient à A »,
« x est élément de A »,
« x est dans A »,
« A a pour élément x »,
« A possède x »,
ou parfois « A contient x » (il y a ambiguïté cependant dans ce dernier cas, A contient x peut signifier que x est un sous-ensemble de A, c’est-à-dire que x est un ensemble et que tous ses éléments appartiennent à A, ce qui est très différent de « x appartient à A »).
Le symbole « ∈ », dérive de la lettre grecque ε (epsilon) introduite par Giuseppe Peano dès 1889. Pour Peano « x ε A » se lit « x est un A », par exemple « x ε N » se lit « x est un entier positif ou nul». Le ε renvoie à l'initiale du mot « est » (en latin, langue de l'article de Peano de 1889 !), en français, ou en italien (« è »). Bertrand Russell reprend les notations de Peano en 1903 dans les Principles of Mathematics, ouvrage qui va participer à leur diffusion, et où est utilisée la forme arrondie vieillie du epsilon : « ϵ », en usage dans l'édition mathématique anglo-saxonne.
Comme souvent pour les relations, on barre ce symbole pour indiquer sa négation, la non-appartenance d’un objet à un ensemble :
-
« z ∉ A » signifie « z n’appartient pas à A ».
Égalité de deux ensembles
En mathématiques – et pas seulement en mathématiques d'ailleurs –, on considère que deux objets sont égaux quand ils ont les mêmes propriétés, que l'on ne peut donc les distinguer l'un de l'autre – c'est la définition de l'égalité de Leibniz. Dire quand deux objets sont égaux, c'est-à-dire quand deux expressions désignent en fait le même objet, c'est donc donner une information sur ce que sont ces objets. En théorie des ensembles on décide qu'un ensemble est complètement caractérisé par ses éléments, son extension, alors qu'il peut avoir plusieurs définitions. Par exemple, il n'y a pas lieu de distinguer l'ensemble des entiers différents d'eux-mêmes et l'ensemble des entiers supérieurs à tous les nombres premiers : ces deux ensembles sont tous les deux vides, donc égaux – ils ont bien les mêmes éléments –, même s'ils ont des définitions différentes, et sont vides pour des raisons très différentes.
On dira donc que deux ensembles A et B sont égaux (on le notera comme d'habitude A = B) quand ils ont exactement les mêmes éléments. Cette propriété est connue sous le nom d'extensionnalité :
(Extensionnalité) A = B si et seulement si ∀x (x ∈ A ⇔ x ∈ B)
où « ⇔ » désigne l'équivalence logique. Deux ensembles qui ont les mêmes éléments sont bien identiques : tout ce qui peut être dit de l'un peut être dit de l'autre. Si nous nous représentons les deux ensembles comme des sacs étiquetés chacun par leur nom, s’ils sont égaux, alors il s’agit en fait d’un seul et même sac avec deux étiquettes. Par contre, les propriétés d’un ensemble ne dépendent absolument pas de la nature ou de la forme du sac, seulement de son contenu.
Ainsi un ensemble est complètement déterminé par ses éléments. Quand un ensemble est fini, il est donc possible de le définir en donnant la liste de ses éléments, que l'on note traditionnellement entre accolades. Par exemple l'ensemble auxquels appartiennent les éléments 2, 3, et 5, et seulement ces éléments, est noté {2, 3, 5}. L'ensemble est défini en extension.
Mais on ne peut procéder ainsi en toute généralité, on ne pourrait définir ainsi un ensemble infini. Même si quelques artifices de notation qui ressemblent à la notation en extension sont possibles (voir ci-après), la façon la plus générale de définir un ensemble est de donner une propriété caractéristique des éléments de cet ensemble. Par exemple, on pourra définir l'ensemble des nombres premiers par une propriété caractéristique de ceux-ci : être différent de 1 et avoir pour seuls diviseurs 1 et lui-même. On parle de définition en compréhension. L’ensemble {2, 3, 5} peut être défini en compréhension comme l’ensemble de tous les nombres premiers inférieurs à 6. La définition en extension des ensembles finis peut être vue comme un cas particulier simple de définition en compréhension : par exemple l'ensemble {2, 3, 5} est caractérisé par la propriété, pour un nombre entier, d'être égal à 2 ou à 3 ou à 5.
Ensembles finis
Quand on parle d'ensembles finis, c'est en un sens intuitif, sans avoir vraiment défini cette notion. Un ensemble est fini quand on peut compter ses éléments à l'aide d'entiers tous plus petits qu'un entier donné.
Les ensembles finis peuvent être définis en extension, par la liste de leurs éléments, et décrits comme tels ; on place la liste des éléments d'un ensemble entre accolades, comme on l'a déjà vu pour l'ensemble {2, 3, 5}. Par exemple, l'ensemble des jours de la semaine peut être représenté par { lundi, mardi, mercredi, jeudi, vendredi, samedi, dimanche }.
La notation d'un ensemble en extension n'est pas unique : un même ensemble peut être noté en extension de façon différentes.
L’ordre des éléments est sans importance, par exemple { 1, 2 } = { 2, 1 }.
La répétition d’éléments entre les accolades ne modifie pas l’ensemble :
-
toujours avec le même exemple, { 1, 2, 2 } = { 1, 1, 1, 2 } = { 1, 2 }.
À cause de la propriété d'extensionnalité, il n'est pas question de distinguer des ensembles par le nombre de répétitions d'un même élément à ces ensembles : un élément appartient ou n'appartient pas à un ensemble, il ne peut appartenir à un ensemble une, deux, ou trois fois…
On pourrait imposer que la notation se fasse sans répétitions, ce serait assez malcommode dès qu'interviennent des variables : on ne pourrait noter un ensemble en extension sans devoir supposer que ses éléments sont distincts.
Il peut arriver que l'on ait besoin d'ensemble « avec répétition », dans le cas fini, il s'agit plus justement, de suites finies à l'ordre des éléments près, on définit alors la notion de multiensemble fini (qui peut se définir à partir de la notion de suite finie).
Les ensembles réduits à un seul élément sont appelés singletons. Par exemple l'ensemble qui contient pour seul élément 0 est appelé « singleton 0 » et noté {0}.
Les ensembles qui ont exactement deux éléments sont appelées paires, la paire des éléments 1 et 2, notée {1,2}, ne doit pas être confondue avec le couple (1,2), qui a un ordre déterminé.
Quand on axiomatise la théorie des ensembles, les paires (et singletons) jouent un rôle particulier, voir l'article Axiome de la paire.
Par extensionnalité, il n'y a qu'un seul ensemble sans éléments, l'ensemble vide, que l'on note ∅ ou { }.
Définition d’un ensemble en compréhension
Un ensemble peut être défini en compréhension, c’est-à-dire qu'on le définit par une propriété caractéristique parmi les éléments d'un ensemble donné. Ainsi l'ensemble des entiers naturels pairs est clairement défini en compréhension, par la propriété « être pair » parmi les entiers naturels. On peut utiliser la notation d'un ensemble en compréhension, par exemple pour l'ensemble des entiers naturels pairs, on écrira (ℕ désignant l'ensemble des entiers naturels) :
.
On définira de la même façon (ℤ désignant l'ensemble des entiers relatifs) :
l'ensemble des entiers relatifs compris entre -7 et 23 ;
l'ensemble des carrés parfaits non nuls.
La formulation générale est :
-
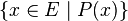
Cette construction a besoin d'un ensemble déjà existant E et d'une propriété P définie sur tous les éléments de E. Elle permet donc de construire des sous-ensembles mais pas la réunion d'une famille d'ensembles, ni l'ensemble des parties d'un ensemble, ni même les ensembles finis définis par la liste de leurs éléments comme au paragraphe précédent. On pourrait pourtant écrire, par exemple pour l'ensemble des parties P(E) = { A | A ⊂ E }
Il n'est pas pour autant possible de définir un ensemble par n'importe quelle propriété, et lever entièrement la restriction de la compréhension. Si c'était le cas on pourrait définir l'ensemble {x | x ∉ x}, ce qui conduit à une contradiction (c'est le paradoxe de Russell). La restriction de la compréhension à un ensemble connu protège contre ce genre de paradoxes, elle correspond directement au schéma d'axiomes de compréhension de la théorie de Zermelo. Cette restriction ne peut se lever que dans des cas particuliers précis, qui correspondent à d'autres axiomes de la théorie de Zermelo (axiome de la paire, axiome de la réunion, axiome de l'ensemble des parties).
On n'a pas dit ce que l'on entendait par « propriété » ou « condition ». Malgré la restriction précédente, on ne peut tout autoriser, sous peine d'autres paradoxes comme le paradoxe de Richard ou le paradoxe de Berry, qui fait intervenir, par exemple, « l'ensemble des entiers naturels définissables en moins de quinze mots français ». Il est nécessaire de préciser le langage dans lequel on peut définir ces conditions. En particulier ce langage doit être défini a priori, et ne peut être étendu qu'à l'aide de définitions qui sont soit de simples abréviations, soit résultent de preuves d'existence et d'unicité.
Ensemble défini comme image directe
Pour noter l'ensemble des carrés parfaits non nuls (voir exemple au paragraphe précédent) on peut utiliser la notation plus concise :
-

dont la forme générale est :
-
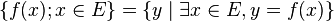
Elle représente l'ensemble des images d'un ensemble E par une application f. L'ensemble obtenu s'appelle image directe de E par f. Il s'agit d'une variante de la notation en compréhension ci-dessus. Elle se déduit de celle-ci, en utilisant la définition d'une fonction, si F est l'ensemble d'arrivée de la fonction f :
-
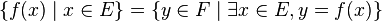 .
.
De cette notation dérivent d'autres notations faciles à comprendre
-
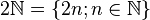
-
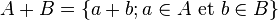
-
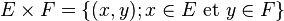
-
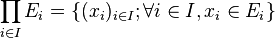
Ces notations ont leur avantage et leur inconvénient. D'un côté, elles facilitent une compréhension immédiate des ensembles considérés et rendent accessibles à l'intuition des objets plus compliqués. D'un autre côté, ces notations masquent un quantificateur existentiel indispensable dès lors que l'on veut utiliser cet ensemble.
Autres notations
Il existe d'autres notations commodes, en particulier pour les ensembles de nombres, et plus généralement pour les ensembles totalement ordonnés.
On peut utiliser des points de suspension, pour des notations inspirées de la notation en extension pour des ensembles de cardinalité infinie, ou finie mais non déterminée. Par exemple, l’ensemble des entiers naturels peut se noter par : ℕ = { 0, 1, 2, 3, … }. S'il est clair par ailleurs que n désigne un entier naturel, {1, 2, … , n}, voire {1, … , n} désigne en général l'ensemble des entiers supérieurs ou égaux à 1 et inférieurs ou égaux à n. De même on peut écrire ℤ = { … , –3, –2, –1, 0, 1, 2, 3, … }. Quand il y a un procédé itératif simple pour engendrer les éléments de l'ensemble, on peut se risquer à des notations comme {0, 2, 4, 6, … } pour l'ensemble des entiers naturels pairs, etc. On peut bien sûr utiliser ces notations pour des ensembles ayant « beaucoup » d'éléments, {1, 2, … , 1000} plutôt que d'écrire les mille premiers nombres entiers non nuls, ou encore { 3, 5, … , 21 } plutôt que { 3, 5, 7, 9, 11, 13, 15, 17, 19, 21 }.
Toutes ces notations ne sont pas systématiques, ni universelles, et pour les dernières au moins, pas très rigoureuses. On peut encore signaler, la notation, rigoureuse celle-ci, de certains sous-ensembles de la droite réelle, les intervalles.
Par abus de notation, parfois on ne note pas la variable dans la définition en compréhension, mais seulement la propriété. Ainsi on note un ensemble en plaçant entre accolades la nature, ou une propriété caractéristique, des objets qui lui appartiennent. Par exemple la notation {chiens} désigne l’ensemble de tous les chiens ; pour prendre un exemple plus mathématique, on pourrait écrire parfois {pairs} pour l'ensemble des nombres pairs.

 词典释义:
词典释义:
 , 一起, 一块儿
, 一起, 一块儿
 。
。 居
居 时, 一齐
时, 一齐 时讲话,让皮埃尔讲。
时讲话,让皮埃尔讲。 时, 一致, 统一, 协调;
时, 一致, 统一, 协调;  协调。
协调。 常
常 天气。
天气。 期里一起调情
期里一起调情
 集
集 相交集
相交集 可约集
可约集 形集
形集 构集
构集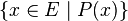

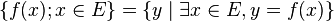
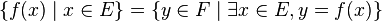 .
.