hyperbolique是什么意思_hyperbolique的常见用法_近义词

词典释义

a.
1. 【修辞】

expression hyperbolique

表达方式

2. 【数学】双

线

, 双

性

fonctions hyperboliques双

函数

近义、反义、派生词

近义词：

ampoulé, boursouflé, déclamatoire, emphatique, grandiloquent, pompeux, être exagéré, dithyrambique, outrancier, outré

反义词：

mesuré, simple

联想词

elliptique 椭圆

; géométrique

何

; algébrique 代数

; convexe 凸出

，隆起

，凸状

; sphérique 球状

，球

; linéaire 线

，线状

，线条

，用线条表现

; mathématique 数学

; conique 圆锥

，锥

n.f.【数学】圆锥

线, 二次

线; symétrique 匀称

; cubique 立方体

，立方

; cyclique 周期性

，循环

;

当代法汉科技词典

hyperbolique adj. 双[线]

fonction hyperbolique 双函数

fonction hyperbolique inverse 反双函数

involution hyperbolique 双对合

navigation hyperbolique 双线航行

paraboloïde hyperbolique 马鞍面

ultra hyperbolique adj. 超双

短语搭配

fonctions hyperboliques双曲函数

expression hyperbolique夸张的表达方式

involution hyperbolique双曲对合

compliment hyperbolique过分的颂扬

paraboloïde hyperbolique双曲抛物面;马鞍形面

navigation hyperbolique双曲线航行

conchoïde hyperbolique双曲蚌线

ultra hyperbolique超双曲的

fonction hyperbolique双曲函数

un style hyperbolique夸张的风格

法语百科

Une demi-droite passant par l'origine intersecte l'hyperbole d'équation x2 – y2 = 1 au point (cosha, sinha), où a est le double de l'aire algébrique de la surface délimitée par la demi-droite, l'hyperbole et l'axe des x. Voir aussi une version animée de ce schéma, avec une comparaison avec les fonctions trigonométriques.

Une demi-droite passant par l'origine intersecte l'hyperbole d'équation x – y = 1 au point (cosha, sinha), où a est le double de l'aire algébrique de la surface délimitée par la demi-droite, l'hyperbole et l'axe des x. Voir aussi une version animée de ce schéma, avec une comparaison avec les fonctions trigonométriques.

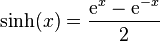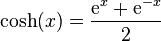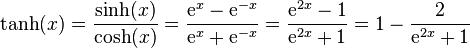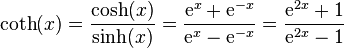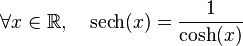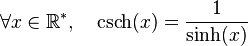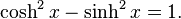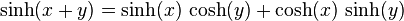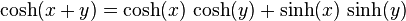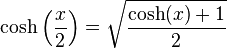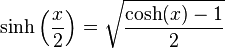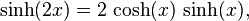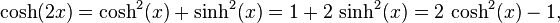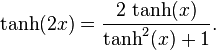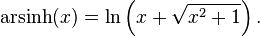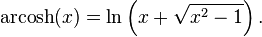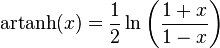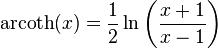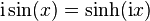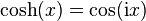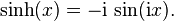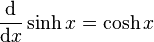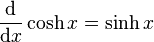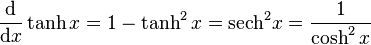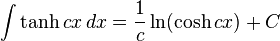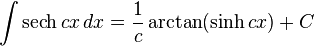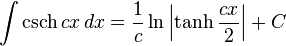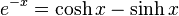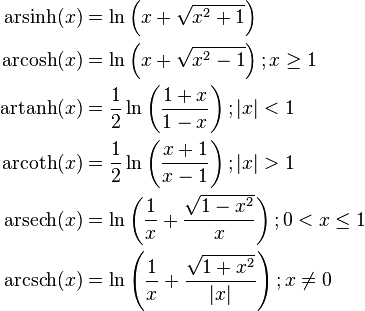
En mathématiques, on appelle fonctions hyperboliques les fonctions cosinus hyperbolique, sinus hyperbolique et tangente hyperbolique. Les noms « sinus », « cosinus » et « tangente » proviennent de leur ressemblance avec les fonctions trigonométriques (dites « circulaires » car en relation avec le cercle unité x + y = 1) et le terme « hyperbolique » provient de leur relation avec l'hyperbole d'équation x – y = 1.

Elles sont utilisées en analyse pour le calcul intégral, la résolution des équations différentielles mais aussi en géométrie hyperbolique.

Histoire

Les fonctions hyperboliques ont été inventées par le jésuite Vincenzo Riccati dans les années 1760 alors qu'il cherchait, avec son collègue Saladini, à calculer l'aire sous l'hyperbole d'équation x – y = 1. La méthode géométrique qu'il employa alors était très similaire à celle que l'on peut utiliser pour calculer l'aire d'un cercle d'équation x + y = 1. Le calcul de l'aire du cercle fait intervenir les fonctions trigonométriques classiques que Riccati nommait cosinus et sinus circulaires. Par analogie, il appela alors les fonctions qu'il venait de créer cosinus et sinus hyperboliques. Ce fut un choix heureux, car cette ressemblance ne s'arrête pas à la méthode de calcul d'aire mais aussi à toutes les formules trigonométriques. Cependant, pourtant au fait du travail de son contemporain Euler, il n'utilisa pas la fonction exponentielle pour les définir mais seulement des considérations géométriques. L'autre grand mathématicien ayant étudié les fonctions hyperboliques est Jean-Henri Lambert, qui en fit une étude complète en 1770. Cette quasi simultanéité fait que l'on attribue parfois à Lambert la paternité des fonctions hyperboliques, bien que les écrits de Riccati lui soient antérieurs de quelques années.

Définitions

Les fonctions hyperboliques sont analogues aux fonctions trigonométriques ou fonctions circulaires. Ce sont les fonctions :

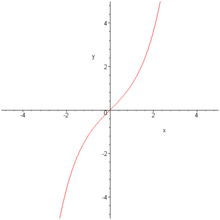
Sinus hyperbolique

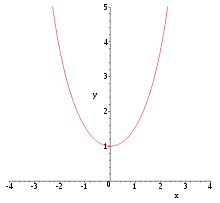
Cosinus hyperbolique

Tangente hyperbolique

Sinus hyperbolique

Définie comme étant la partie impaire de la fonction exponentielle, c’est-à-dire par :

\operatorname{sinh}(x) = \frac{{\rm e}^{x}\rm e}^{-x}}2

sinh — ou sh — est une bijection de classe C de ℝ dans ℝ strictement croissante, et impaire. Sa dérivée est le cosinus hyperbolique. Son application réciproque est l'argument sinus hyperbolique.

Cosinus hyperbolique

Définie comme étant la partie paire de la fonction exponentielle, c’est-à-dire par :

\operatorname{cosh}(x) = \frac{{\rm e}^x+{\rm e}^{-x}}2

cosh — ou ch — est une application de ℝ dans [1, +∞[ strictement croissante sur ℝ, et paire. cosh est de classe C sur ℝ et sa dérivée est le sinus hyperbolique. Sa restriction à ℝ est une bijection à valeurs dans [1, +∞[ dont l'application réciproque est l'argument cosinus hyperbolique.

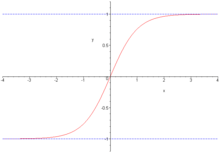
Tangente hyperbolique

Définie par :

\operatorname{tanh}(x) = \frac{\operatorname{sinh}(x)}{\operatorname{cosh}(x)} = \frac{{\rm e}^x\rm e}^{-x}}{{\rm e}^x+{\rm e}^{-x}}=\frac{{\rm e}^{2x1}{{\rm e}^{2x}+1}=1-\frac 2{{\rm e}^{2x}+1}

tanh — ou th — est une bijection de classe C de ℝ dans ]–1, 1[ strictement croissante, et impaire. Sa dérivée est . Son application réciproque est l'argument tangente hyperbolique.

Cotangente hyperbolique

Définie par :

\coth(x) = \frac{\operatorname{cosh}(x)}{\operatorname{sinh}(x)} = \frac{{\rm e}^x+{\rm e}^{-x}}{{\rm e}^x\rm e}^{-x}}=\frac{{\rm e}^{2x}+1}{{\rm e}^{2x1}

coth est une bijection de classe C de ℝ* dans ]–∞, –1[∪]1, +∞[. Sa dérivée est . Son application réciproque est l'argument cotangente hyperbolique.

Sécante hyperbolique

Définie par :

\forall x \in \R,\quad\operatorname{sech}(x) = \frac{1}{\operatorname{cosh}(x)}

Cosécante hyperbolique

Définie par :

\forall x \in \R^*,\quad\operatorname{csch}(x) = \frac{1}{\operatorname{sinh}(x)}

Tableau de variations

Les fonctions sinh, tanh, et coth sont impaires et la fonction cosh est paire, on peut donc réduire leur domaine d'étude à $[0, +\infty[$ .

x	0		+ $\infty$
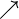cosh x	1	$\nearrow$	+ $\infty$
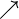sinh x	0	$\nearrow$	+ $\infty$
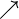tanh x	0	$\nearrow$	+1
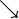coth x	+ $\infty$	$\searrow$	+1

Propriétés

Par construction, 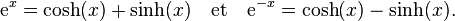${\rm e}^x= \operatorname{cosh}(x) + \operatorname{sinh}(x)\quad{\rm et}\quad{\rm e}^{-x} = \operatorname{cosh}(x) - \operatorname{sinh}(x).$

On en déduit la formule suivante :

\operatorname{cosh}^2x - \operatorname{sinh}^2x = 1.

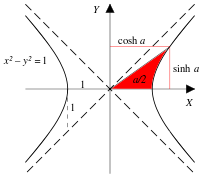
De même que les points (cosx, sinx) décrivent un cercle lorsque x parcourt ℝ, les points (coshx, shx) décrivent une branche d'hyperbole.

Le paramètre x ne peut pas être interprété comme un angle, ni comme une longueur d'arc ; les fonctions hyperboliques sont périodiques, mais de période imaginaire pure.

La fonction cosh admet 1 pour minimum, en 0.

La fonction sinh est impaire et ainsi sinh(0) = 0.

Les fonctions hyperboliques satisfont à des relations, très ressemblantes aux identités trigonométriques. En fait, la règle d'Osborn dit que l'on peut convertir n'importe quelle identité trigonométrique en une identité hyperbolique en la développant complètement à l'aide de puissances entières de sinus et cosinus, changeant sin en sinh et cos en cosh, et remplaçant le signe de chaque terme qui contient un produit de deux sinus en son opposé.

Cela nous permet d'obtenir par exemple, les formules d'addition et de soustraction :

\operatorname{sinh}(x + y) = \operatorname{sinh}(x)\, \operatorname{cosh}(y) + \operatorname{cosh}(x)\, \operatorname{sinh}(y)

\operatorname{cosh}(x + y) = \operatorname{cosh}(x)\, \operatorname{cosh}(y) + \operatorname{sinh}(x)\, \operatorname{sinh}(y)

\operatorname{sinh}(x - y) = \operatorname{sinh}(x)\, \operatorname{cosh}(y) - \operatorname{cosh}(x)\, \operatorname{sinh}(y)

\operatorname{cosh}(x - y) = \operatorname{cosh}(x)\, \operatorname{cosh}(y) - \operatorname{sinh}(x)\, \operatorname{sinh}(y)

et des « formules d'angle moitié » (la deuxième étant valide si x est positif ou nul) :

\operatorname{cosh}\left(\frac{x}{2}\right) = \sqrt{\frac{\operatorname{cosh}(x) + 1}{2}}

\operatorname{sinh}\left(\frac{x}{2}\right) = \sqrt{\frac{\operatorname{cosh}(x)-1}{2}}

De ces expressions on déduit les formules suivantes relatives à la tangente hyperbolique : 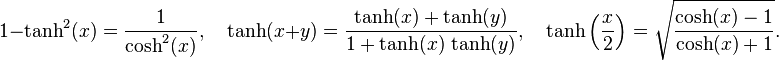$1 - \operatorname{tanh}^2(x) = \frac{1}{\operatorname{cosh}^2(x)},\quad\operatorname{tanh}(x+y) = \frac{\operatorname{tanh}(x)+\operatorname{tanh}(y)}{1+\operatorname{tanh}(x)\,\operatorname{tanh}(y)},\quad\operatorname{tanh}\left(\frac{x}{2}\right) = \sqrt{\frac{\operatorname{cosh}(x) - 1}{\operatorname{cosh}(x)+1}}.$

On a de même :

\operatorname{sinh}(2 x) = 2\, \operatorname{cosh}(x)\,\operatorname{sinh}(x),

\operatorname{cosh}(2 x) = \operatorname{cosh}^2(x) + \operatorname{sinh}^2(x) = 1 + 2\,\operatorname{sinh}^2(x) = 2\, \operatorname{cosh}^2(x) - 1,

\operatorname{tanh}(2 x) = \frac{2\, \operatorname{tanh}(x)}{\operatorname{tanh}^2(x) + 1}.

La fonction cosinus hyperbolique est convexe. Elle intervient dans la définition de la chaînette, laquelle correspond à la forme que prend un câble suspendu à ses extrémités et soumis à son propre poids.

Puisque la fonction exponentielle peut être prolongée à l'ensemble des nombres complexes, nous pouvons aussi étendre les définitions des fonctions hyperboliques à l'ensemble des nombres complexes. Les fonctions sinus hyperbolique et cosinus hyperbolique sont alors holomorphes et même entières.

Applications réciproques

Argument sinus hyperbolique

arsinh — ou argsh — est l'application réciproque de sinh. C'est une bijection de ℝ dans ℝ, impaire et strictement croissante. arsinh est dérivable sur ℝ et sa dérivée est . arsinh admet la forme logarithmique suivante :

\operatorname{arsinh}(x) = \ln\left(x + \sqrt{x^2 +1 }\right).

Argument cosinus hyperbolique

$arcosh$ — ou $argch$ — est l'application réciproque de la restriction de $cosh$ dans ℝ. C'est une bijection de $[1, +\infty[$ dans ℝ, strictement croissante. $arcosh$ est dérivable sur $]1, +\infty[$ et sa dérivée est 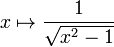$x \mapsto \frac{1}{\sqrt{x^2-1}}$ . $arcosh$ admet une forme logarithmique :

\operatorname{arcosh}(x) = \ln\left(x + \sqrt{x^2 -1}\right).

Argument tangente hyperbolique

$artanh$ — ou $argth$ — est l'application réciproque de $tanh$ . C'est une bijection de $]-1, 1[$ dans ℝ, impaire, strictement croissante. $artanh$ est dérivable sur $]-1, 1[$ et sa dérivée est $x \mapsto \tfrac{1}{1-x^2}$ . $artanh$ admet une forme logarithmique :

\operatorname{artanh}(x) = \frac{1}{2}\ln\left(\frac{1+x}{1-x}\right)

Argument cotangente hyperbolique

$arcoth$ — ou $argcoth$ — est l'application réciproque de $coth$ . C'est une bijection de $]-\infty, -1[\cup]1, +\infty[$ dans ℝ*. $arcoth$ est dérivable sur $]-\infty, -1[\cup]1, +\infty[$ et sa dérivée est $x \mapsto \tfrac{1}{1-x^2}$ . $arcoth$ admet une forme logarithmique :

\operatorname{arcoth}(x) = \frac{1}{2}\ln\left(\frac{x+1}{x-1}\right)

Démonstrations de ces résultats

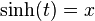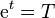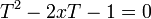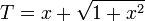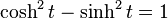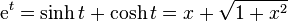Le calcul explicite de ces formes logarithmiques revient à résoudre, par exemple, l'équation $\operatorname{sinh} (t)= x$ ; posant ${\rm e}^t=T$ , on est amené à l'équation du second degré $T^2-2xT-1=0$ , dont la seule solution positive est $T=x+\sqrt {1+x^2}$ , mais il peut être plus simple de remarquer que, puisque $\operatorname{cosh}^2t-\operatorname{sinh}^2t=1$ , on aura ${\rm e}^t=\operatorname{sinh} t+\operatorname{cosh} t= x+\sqrt {1+x^2}$ .

Relations entre fonctions hyperboliques et fonctions circulaires

Des formules d'Euler, on déduit immédiatement :

\cos(x) = \operatorname{cosh}(\mathrm i x)

\mathrm i\sin(x) = \operatorname{sinh}(\mathrm i x)

Ou encore:

\operatorname{cosh}(x) = \cos(\mathrm i x)

\operatorname{sinh}(x) = -\mathrm i\,\sin(\mathrm i x).

D'autres relations entre fonctions hyperboliques et circulaires sont données par la fonction de Gudermann ou Gudermannien. Elles ont été dégagées par le mathématicien Christoph Gudermann. Le Gudermannien θ de t peut être défini par sinh t = tan θ. On en déduit de nombreuses relations entre les fonctions trigonométrique de θ et les fonctions hyperboliques de t.

中文百科

射线出原点交单位双曲线

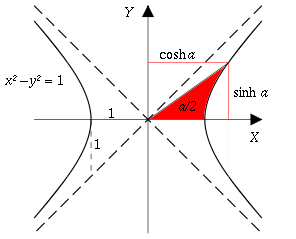
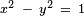\scriptstyle x^2\ -\ y^2\ =\ 1

于点

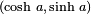\scriptstyle (\cosh\,a,\,\sinh\,a)

，这里的

\scriptstyle a

是射线、双曲线和

\scriptstyle x

轴围成的面积的二倍。对于双曲在线位于x轴下方的点，这个面积被认为是负值。

在数学中，双曲函数是一类与常见的三角函数（也叫圆函数）类似的函数。最基本的双曲函数是双曲正弦函数和双曲余弦函数，从它们可以导出双曲正切函数等，其推导也类似于三角函数的推导。双曲函数的反函数称为反双曲函数。

双曲函数的定义域是实数，其自变量的值叫做双曲角。双曲函数出现于某些重要的线性微分方程的解中，譬如说定义悬链线和拉普拉斯方程。

基本定义

历史

虚数圆角定义

双曲角经常定义得如同虚数圆角。实际上，如果x是实数而i = −1，则所以双曲函数cosh和sinh可以通过圆函数来定义。这些恒等式不是从圆或旋转得来的，它们应当以无穷级数的方式来理解。特别是，可以将指数函数表达为由偶次项和奇次项组成，前者形成cosh函数，后者形成了sinh函数。cos函数的无穷级数可从cosh得出，通过把它变为交错级数，而sin函数可来自将sinh变为交错级数。上面的恒等式使用虚数i，从三角函数的级数的项中去掉交错因子(−1)，来恢复为指数函数的那两部份级数。双曲函数可以通过虚数圆角定义为：这些复数形式的定义得出自欧拉公式。

与三角函数的模拟

正弦同样是从x轴到曲线的半弦。

余弦同样是从y轴到曲线的半弦（图中的余弦是长方形的另一条边）。

正切同样是过x轴上单位点（1,0）在曲在线的切线到终边的长度。

余切同样是从y轴与过终边和曲线交点的切线与y轴的交点和曲线连接之长度。

正割同样是在一个有正切和单位长的直角三角形上，但边不一样。

余割同样是y轴与过终边和曲线交点的切线与y轴的交点和原点之距离。

角的量值可以从0到无限大，但α实际上只会介于0到（360度）之间，其余是α的同界角，再绕着圆旋转，故三角函数可以有周期。双曲角的量值可以从0到无限大，但α实际上不会超过（45度），故无法如三角函数一样有周期性。

恒等式

加法公式：

二倍角公式：

半角公式：

三倍角公式：

差角公式：

双曲函数的导数

\frac{\mathrm{d}}{\mathrm{d}x}\sinh x = \cosh x \,

\frac{\mathrm{d}}{\mathrm{d}x}\cosh x = \sinh x \,

\frac{\mathrm{d}}{\mathrm{d}x}\tanh x = 1 - \tanh^2 x = \hbox{sech}^2 x = \frac{1}{\cosh^2 x} \,

双曲函数的泰勒展开式

双曲函数也可以以泰勒级数展开: （罗朗级数）（罗朗级数）其中是第n项伯努利数是第n项欧拉数

双曲函数的积分

\int\sinh cx\,dx = \frac{1}{c}\cosh cx + C

\int\cosh cx\,dx = \frac{1}{c}\sinh cx + C

\int \tanh cx\,dx = \frac{1}{c}\ln(\cosh cx) + C

\int \coth cx\,dx = \frac{1}{c}\ln(\sinh cx) + C

\int \operatorname{sech} cx\,dx = \frac{1}{c}\arctan (\sinh cx) + C

\int \operatorname{csch} cx\,dx = \frac{1}{c}\ln\left|\tanh\frac{cx}{2}\right| + C

与指数函数的关系

从双曲正弦和余弦的定义，可以得出如下恒等式:

e^x = \cosh x + \sinh x

和

e^{-x} = \cosh x - \sinh x

复数的双曲函数

因为指数函数可以定义为任何复数参数，也可以扩展双曲函数的定义为复数参数。函数sinh z和cosh z是全纯函数。指数函数与三角函数的关系由欧拉公式给出：所以: 因此，双曲函数是关于虚部有周期的，周期为 (对双曲正切和余切是).

反双曲函数

反双曲函数是双曲函数的反函数。它们的定义为：

\begin{align} \operatorname {arsinh} (x) &= \ln \left(x + \sqrt{x^{2} + 1} \right) \\ \operatorname {arcosh} (x) &= \ln \left(x + \sqrt{x^{2} - 1} \right); x \ge 1 \\ \operatorname {artanh} (x) &= \frac{1}{2}\ln \left( \frac{1 + x}{1 - x} \right); \left| x \right| < 1 \\ \operatorname {arcoth} (x) &= \frac{1}{2}\ln \left( \frac{x + 1}{x - 1} \right); \left| x \right| > 1 \\ \operatorname {arsech} (x) &= \ln \left( \frac{1}{x} + \frac{\sqrt{1 - x^{2}}}{x} \right); 0 < x \le 1 \\ \operatorname {arcsch} (x) &= \ln \left( \frac{1}{x} + \frac{\sqrt{1 + x^{2}}}{\left| x \right|} \right); x \ne 0 \end{align}

法法词典

hyperbolique adjectif ( même forme au masculin et au féminin, pluriel hyperboliques )

1. linguistique : en rhétorique caractérisé par l'emphase et l'exagération

les envolées hyperboliques d'un orateur
2. mathématiques : en géométrie que l'on peut représenter par une hyperbole géométrique

l'orbite hyperbolique d'une comète