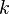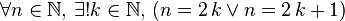Heureusement, moi je sais faire des bateaux en papier et on a pris les feuilles du livre d'arithmétique.
幸好我会用纸叠小船,我们从算术书上撕下来一些纸。
[小淘气尼古拉绝版故事 Le Petit Nicolas]
Le photographe était là, aussi, avec son appareil et la maîtresse lui a dit qu'il fallait faire vite, sinon, nous allions rater notre cours d'arithmétique.
摄影师守着他的相机也在操场上,老师对他说,尽量快些,否则就要错过算术课了。
[小淘气尼古拉绝版故事 Le Petit Nicolas]
Agnan, qui est le premier de la classe et le chouchou de la maîtresse, a dit que ce serait dommage de ne pas avoir arithmétique, parce qu'il aimait ça et qu'il avait bien fait tous ses problèmes.
阿尼昂,既是班上的第一名也是老师的宠儿。他说,如果不能上算术课,那就太遗憾了,这可是他最喜欢的课,而且,他可以解出所有的算术题。
[小淘气尼古拉绝版故事 Le Petit Nicolas]
Alceste m'a répondu que cet après-midi on avait arithmétique, alors j'ai dit «bon» et nous ne sommes pas allés à l'école.
亚斯特说可是今天下午有算术课,我回答:“好吧”,结果我们就没去上学。
[小淘气尼古拉绝版故事 Le Petit Nicolas]
«Vous allez me conjuguer le verbe: je ne dois pas être grossier envers un camarade qui est chargé de me surveiller et qui veut me faire faire des problèmes d'arithmétique.»
“请您给我做下面这个动词变位:我不应该对负责看管我的并且想要帮我解决算术题的同学粗鲁地讲话” 。
[小淘气尼古拉绝版故事 Le Petit Nicolas]
Sa femme, grande, forte, résolue, avec la voix haute et la décision rapide, était l'ordre et l'arithmétique de la maison de commerce, qu'il animait par son activité joyeuse.
他的妻子,高大,强壮,沉着,大嗓子,而且主意又快又坚决,在那个被他的兴高采烈的活动力所鼓舞的店里,简直是一种权威。
[莫泊桑短篇小说精选集]
Il écrivait bien, et savait parfaitement l’arithmétique. L’anabaptiste Jacques en fit son teneur de livres.
他笔下很来得,又精通算术。雅各派他当账房。
[憨第德 Candide]
Un jour, après les cours, il m'a demandé de rester dans la classe et a écrit une dizaine de suites arithmétiques sur le tableau noir.
有一天下课后他把我留下,在黑板上写了十几个数列。
[《三体》法语版]
Il s'est fait virer de son stage d'arithmétique avancée.
他被高级算术实习解雇了。
[Groom 第二季]
Et la phrase se comprend sur une construction arithmétique et financière : régler son compte, c’est d’abord régler ses dettes.
这句话可以从算术和金融结构上理解:结清账目首先是清偿债务。
[Les mots de l'actualité - 2017年合集]
Le photographe était là, aussi, avec son appareil et la maitresse lui a dit qu’il fallait faire vite, sinon, nous allions rater notre cours d’arithmétique.
照相师也已经到了,带着他的照相机。班主任提醒他,拍照得快一点,否则我们会耽误上算术课。
Agnan, qui est le premier de la classe et le chouchou de la maîtresse, a dit que ce serait dommage de ne pas avoir arithmétique, parce qu'il aimait ça et qu'il avait bien fait tous ses problèmes.
阿南是我们班排名第一也是老师最喜欢的学生,他说如果赶不上算术课就太可惜了,因为他喜欢算术课而且他把算术难题都解决了。
Agnan, qui est le premier de la classe et le chouchou de la maitresse, a dit que ce serait dommage de ne pas avoir arithmétique, parce qu’il aimait ca et qu’il avait bien fait tous ses problèmes.
AGNAN,是我们班上的第一名,也是班主任老师的心肝宝贝,他说如果耽误了算术课的话,那就太可惜了。因为,他做好了全部的回家作业。
Le photographe était là, aussi, avec son appareil et la maîtresse lui a dit qu'il fallait faire vite, sinon, nous allions rater notre cours d'arithmétique.
摄影师也带着他的照相机到了,他对老师说要大家快一点,要不然我们会赶不上算术课。
Sa femme, grande, forte, résolue, avec la voix haute et la décision rapide, était l'ordre et l'arithmétique de la maison de commerce, qu'il animait par son activité joyeuse.
他的妻子,高大,强壮,沉着,大嗓子,而且主意又快又坚决,在那个被他的兴高采烈的活动力所鼓舞的店里,简直是一种权威。
La maitresse a dit qu’elle nous donnait un dernier avertissement, après ce serait l’arithmétique, alors, on s’est dit qu’il fallait se tenir tranquilles et on a commencé à s’installer.
班主任老师说她最后一次警告我们,否则的话,就上算术课去。
Il est le der en arithmétique!
他的算术是倒数第一!
L'alinéa 1 b), qui fait référence à la correction d'erreurs purement arithmétiques, ne vise pas par exemple un prix soumissionné anormalement bas semblant résulter d'un malentendu ou d'autres erreurs non apparentes dans l'offre.
第(1)(b)款提到纠正纯属计算上的错误,这里既不是指疑为误解造成的异常低价竞标,也不是指从投标书表面来看并不明显的其他错误。”
Il ne faut pas oublier non plus que l'arithmétique de la proposition du groupe du consensus, qui insiste notamment sur la possibilité de réélection pour tous les sièges non permanents et sur la présence permanente des régions, pourrait en fait signifier que les petits pays auraient moins de chances d'être élus, alors que la proposition du Groupe des Quatre leur offre nettement plus de chances, même si elles sont encore limitées.
我们也不要忘记,按照联合一致谋共识方案,尤其是方案着重强调所有非常任理事国可连任和常任,实际上可能意味着小国当选的机会更少,而四国集团方案明显增加小国当选的机会,虽然幅度不是很大。
Je souhaitais simplement faire remarquer la coïncidence arithmétique frappante.
我仅仅指出算术上的这种惊人吻合。
Il a également été dit qu'il faudrait de l'efficacité, mais, encore une fois, comme je l'ai dit plus tôt, l'efficacité n'est pas une constante arithmétique.
另外,还有人说,应该促进效力,但我要再次指出,正如我在前面所说的那样,效力并不是一个算术常项。
Voilà ce qui rend cet organe efficace - pas l'arithmétique, pas la gestion.
使本组织具有效力的正是这种行事方式,不是数字游戏,也不是管理阶层。
L'efficacité n'est pas une notion d'arithmétique ou de gestion; elle est fonction de décisions optimales et justes.
效率不是一个算术或管理概念;它取决于最佳和公正的决定。
En outre, si un maintien de la présence est proposé - je ne suis pas très bon pour citer les statistiques, et probablement pas aussi bon en mathématiques que les membres du mouvement Unis pour un consensus - alors, la conséquence arithmétique sur les autres sièges serait bien pire, même sur ce seul plan arithmétique, que ne l'est la proposition du Groupe des quatre.
此外,如果提议持续存在——我不太善于印证统计数字,也许不如“团结某共识”成员精通数学——那么,对其他席位的算术影响将糟得多,甚至在算术上要比四国集团的建议更糟。
L'UNRWA déclare que la recommandation est acceptée, tout en soulignant que les différences arithmétiques dans les chiffres totaux étaient principalement des différences dues à l'arrondissement des chiffres, et que d'autres résultaient de la modification de la présentation de certaines sections des états financiers et des notes par rapport à l'exercice biennal précédent.
近东救济工程处表示同意这项建议,不过,值得一提的是总数上的算术差别大部分是四舍五入的结果,其余差别是前两年期财务报表和附注某些部分列报方式变化所致。
Aux fins du présent rapport, on entend par évaluation quantitative l'attribution, la comparaison et la manipulation arithmétique de valeurs numériques qu'il s'agisse de valeurs monétaires, de notes, de ratios, de pourcentages ou autres, pour tirer des conclusions.
就本报告来说,量化评价可以界定为指派、比较和计算数值,无论是货币、得分、比例和百分比还是其他类型,以推断出关于所考虑事项的一些结果。
6 Dans le cadre des stratégies nationales de lutte contre la pauvreté, il convient que les États donnent également la priorité à la fourniture de services essentiels aux plus pauvres et à l'investissement dans les ressources humaines, en garantissant l'accès universel à l'éducation primaire, aux soins de santé de base, au renforcement des capacités en matière de bonnes pratiques, à une eau potable propre, à des équipements d'assainissement adéquats et à la justice et en appuyant les programmes d'alphabétisation, d'arithmétique élémentaires et de bonnes pratiques d'hygiène.
6 在其减贫战略中,各国还应优先向最贫困者提供基本服务和人力资源投资,确保人人获得初级教育、基本保健、优秀作业方面的能力建设、清洁饮用水、适当卫生和声张正义,支持扫盲、基本计算能力和良好卫生习惯等计划。
Des commentateurs ont noté que des pourcentages fixes ou d'autres “méthodes arithmétiques” peuvent être arbitraires et mettent en doute leur efficacité, en particulier dans la mesure où ces méthodes peuvent être faussées par des offres dont le prix est élevé par rapport à la moyenne.
有些人在发表评论时指出,任何固定的百分比比例或其他“数学方法”都可能是武断的做法,并对这些做法的效能提出疑问,特别是这些做法可能因投标相对于均价偏高而有所扭曲。
Le secrétariat n'a connaissance d'aucun système qui autorise le rejet d'une offre susceptible d'être anormalement basse sans évaluation (en d'autres termes, le recours à des méthodes arithmétiques ou statistiques pour écarter ce type d'offre n'est pas permis).
秘书处发现,没有一个国家的制度允许未经评标就否决一项可能的低价竞标(即不准许使用数学或统计方法取消低价竞标的资格)。
Les principales méthodes utilisées à cette fin sont des techniques arithmétiques ou statistiques qui permettent de repérer les offres qui sortent de la fourchette normale de prix (“analyse statistique”) en utilisant les informations sur le marché pour déterminer des prix de référence à des fins de comparaison et en analysant la structure du prix des fournisseurs (“analyse des prix”), et en se demandant si une offre particulière semble présenter un risque au stade de l'exécution (“analyse du risque”).
主要识别方法是使用数字或统计学方法查明正常价格范围之外的出价(“统计学分析”),一方面使用市场信息确定比较分析的参考价格并对供应商的价格结构进行分析(“价格分析”),另一方面分析某一投标是否会造成履约风险(“风险分析”)。

 词典释义:
词典释义:
 一清二楚的。〈引申义〉这
一清二楚的。〈引申义〉这 合乎逻辑的。
合乎逻辑的。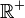 l'ensemble des nombres positifs de
l'ensemble des nombres positifs de 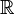 . De même on notera
. De même on notera 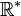 l'ensemble
l'ensemble 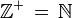 et que
et que 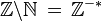 (il s'agit de
(il s'agit de 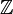 « privé de »
« privé de » 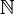 .).
.).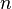 pair est un multiple de 2 et peut être noté
pair est un multiple de 2 et peut être noté 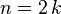 , avec
, avec 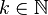 . Un nombre
. Un nombre 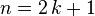 , avec
, avec