Le périmètre du carré vaut ici 8.
Selon Homère, le périmètre de Troie était de 10 200 pas. (Photo des remparts supposés de Troie.)
Le périmètre d'une figure plane est la longueur du bord de cette figure (la longueur du contour de la figure). Le calcul du périmètre sert par exemple à déterminer la quantité de grillage nécessaire à la clôture d'un terrain, le nombre de briques ou de pierres pour la construction d'un mur, etc.
Pour tout polygone, le périmètre vaut la somme des longueurs des côtés du polygone. Il existe des formules simples pour le calcul du périmètre des figures de base, mais le problème devient beaucoup plus ardu pour des figures plus complexes : il fait appel à des calculs d'intégrales ou de limites. Dans ce cas, une méthode consiste à approcher la figure complexe par d'autres, plus simples et mieux connues, pour obtenir une approximation du périmètre voulu.
La question de savoir, pour un périmètre donné, quelle est la surface dont l'aire est maximale (ou isopérimétrie) a été posée très tôt et sa réponse seulement démontrée au XIX siècle.
Le périmètre désigne aussi parfois la courbe qui est le bord d'une surface, plutôt que sa mesure. Le mot périmètre (du grec ancien : περίμετρος) est composé du préfixe péri- qui signifie « autour » et du suffixe -mètre : « mesure ».
Figures de base
Polygone
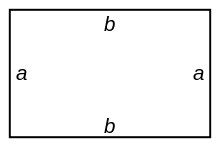
Un rectangle de largeur a et de longueur b.
Le cas des polygones est fondamental, non seulement par sa simplicité, mais aussi parce que de nombreux périmètres sont calculés, en valeur approchée, par une suite de polygones tendant vers ces courbes. Le premier mathématicien connu pour avoir utilisé ce raisonnement fut Archimède qui approcha le périmètre d'un cercle en l'encadrant par celui de polygones réguliers.
Le périmètre d'un polygone est égal à la somme des longueurs de ses côtés.
En particulier, un rectangle de dimensions a et b a pour périmètre 2(a + b). Un polygone équilatéral est un polygone dont tous les côtés ont la même longueur (un losange est un polygone équilatéral à quatre côtés). Pour calculer le périmètre d'un polygone équilatéral, il suffit de multiplier cette longueur par le nombre de côtés.
Un polygone régulier est souvent défini par son nombre de côtés et son rayon, c'est-à-dire la distance constante qui sépare son centre de chacun des sommets. Il est possible de calculer la longueur du côté par un raisonnement de trigonométrie. Si R est le rayon d'un polygone régulier et n le nombre de ses côtés, son périmètre est :
-
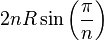 .
.
Ces méthodes sont résumées dans le tableau ci-dessous.
Périmètre de polygones Polygone Formule Variables Triangle a, b et c sont les longueurs des côtés du triangle. Parallélogramme a et b sont les longueurs de deux côtés consécutifs. Polygone équilatéral n est le nombre de côtés et a la longueur de chaque côté. Polygone quelconque où est la longueur du (1, 2, 3… n) côté d'un polygone à n côtés. Polygone régulier convexe n est le nombre de côtés et R la distance entre le centre du polygone régulier et chacun des sommets.
Circonférence d'un cercle
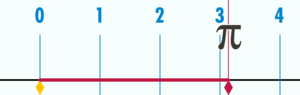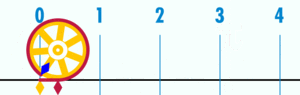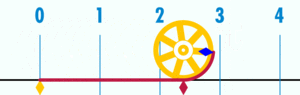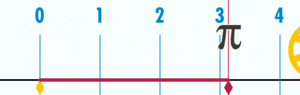
Si le diamètre du cercle est 1, sa circonférence est π.
Le périmètre d'un cercle est proportionnel à son diamètre. C'est-à-dire qu'il existe une constante π (le p grec de périmètre) telle que, quel que soit un cercle de diamètre D et de périmètre P,
-
P = π D.
L'usage du compas ayant favorisé l'utilisation du rayon R du cercle plutôt que de son diamètre, cette formule devient :
- P = 2 π R.
Ces deux formules sont parfaitement équivalentes puisque, pour tout cercle, D = 2 R.
Il suffit, pour calculer le périmètre d'un cercle, de connaître son rayon ou son diamètre et le nombre π. Le problème est que ce nombre n'est pas rationnel (on ne peut pas l'écrire sous la forme d'un quotient de deux entiers) ni même algébrique (il n'est pas la racine d'un polynôme à coefficients entiers). Obtenir une valeur approchée de π aussi précise qu'on le souhaite n'est donc pas évident. La recherche des décimales de π mobilise des connaissances en analyse, algorithmique et informatique.
Le périmètre d'un cercle est souvent appelé circonférence, parfois longueur, le mot périmètre concernant plutôt le disque.
Perception du périmètre

Plus on découpe, plus l'aire diminue et le périmètre augmente.
La citadelle de Neuf-Brisach a un périmètre compliqué. Pour en faire le tour, mieux vaut suivre son enveloppe convexe.
Le périmètre est, avec l'aire, l'une des deux mesures principales des figures géométriques. Il est fréquent de confondre ces deux notions ou de croire que, plus l'une est grande, plus l'autre l'est aussi. En effet l'agrandissement (ou la réduction) d'une figure géométrique fait croître (ou décroître) simultanément son aire et son périmètre. Par exemple, si un terrain est représenté sur une carte à l'échelle 1:10 000, le périmètre réel du terrain peut être calculé en multipliant le périmètre de la représentation par 10 000 et l'aire en multipliant celle de la représentation par 10 000. Il n'existe cependant aucun lien direct entre l'aire et le périmètre d'une figure quelconque. Par exemple, un rectangle possédant une aire égale à un mètre carré peut avoir comme dimensions, en mètres : 0,5 et 2 (donc un périmètre égal à 5 m) mais aussi 0,001 et 1000 (donc un périmètre de plus de 2 000 m). Proclus (V siècle) rapporte que des paysans grecs se sont partagés « équitablement » des champs suivant leurs périmètres, mais avec des aires différentes. Or, la production d'un champ est proportionnelle à l'aire, non au périmètre : certains paysans naïfs ont pu obtenir des champs avec de longs périmètres, mais une aire (et donc une récolte) médiocre.
Lorsqu'on ôte une partie d'une figure, son aire diminue (on a aussi « ôté » une aire). Mais il n'en est pas toujours de même du périmètre. Dans le cas de figure très « découpées », à la confusion aire/périmètre s'ajoute celle avec l'enveloppe convexe de la figure plutôt que son tour au sens strict. L'enveloppe convexe d'une figure est semblable à un élastique qui entourerait cette figure. Sur l'animation ci-contre à gauche, toutes les figures ont la même enveloppe convexe : le grand hexagone initial.
Isopérimétrie

Des yeux à la surface d'un bouillon.
L'isopérimétrie traite, en particulier, la question de trouver la surface la plus vaste possible, pour un périmètre donné. La réponse est intuitive, c'est le disque. Ceci explique pourquoi, notamment, les yeux à la surface d'un bouillon ont une forme circulaire.
Ce problème, d'apparence anodin, fait appel à des théories sophistiquées pour obtenir une démonstration rigoureuse. On simplifie parfois le problème isopérimétrique en limitant les surfaces autorisées. Par exemple on cherche le quadrilatère ou le triangle d'aire la plus vaste possible, toujours pour un périmètre donné. Les solutions respectives sont le carré et le triangle équilatéral. De manière générale, le polygone à n sommets ayant la plus grande surface, à périmètre donné, est celui qui se rapproche le plus du cercle, c'est le polygone régulier.
L'isopérimétrie ne se limite pas à ces questions. On recherche aussi une zone d'aire la plus vaste possible pour un périmètre donné, avec des géométries différentes. Par exemple, dans le cas d'un demi-plan, la réponse est le demi-disque.
Ce concept donne naissance à une famille de théorèmes, dit isopérimétriques, à des majorations dites inégalités isopérimétriques, ainsi qu'à un rapport, appelé quotient isopérimétrique. L'inégalité isopérimétrique indique qu'une surface de périmètre p et d'aire a vérifie la majoration suivante :
-
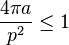
Le terme de gauche, est appelé quotient isopérimétrique, il est égal à 1 si, et seulement si la surface est un disque.
Si l'origine de cette question date d'au moins 2 900 ans, ce n'est qu'en 1895, à l'aide de méthodes dérivées du théorème de Minkowski que la question est définitivement résolue sous sa forme antique. Ces méthodes permettent de démontrer le théorème isopérimétrique et de le généraliser à des dimensions supérieures dans le cas d'une géométrie euclidienne.
Voir l'article isopérimétrie pour les aspects élémentaires de cette question. Des éléments de réponse, faisant usage d'outils mathématiques plus sophistiqués, sont proposés dans l'article Théorème isopérimétrique.
Courbe rectifiable
Mis à part les cas des polygones et des cercles, le périmètre de la plupart des surfaces est malaisé à calculer : il fait intervenir une intégrale qui ne s'exprime pas souvent au moyen de fonctions élémentaires (polynômes, sinus, etc.)
Un exemple : l'ellipse
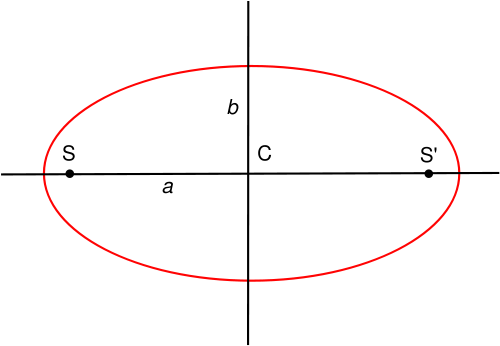
Une ellipse.
L'ellipse peut paraître simple : il ne s'agit après tout que d'un « cercle écrasé ».
Soit une ellipse de demi-grand axe a et de demi-petit axe b.
L'aire est aisée à calculer : 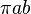 .
.
Mais le périmètre P de l'ellipse ne peut être obtenu qu'à l'aide d'une intégrale elliptique :
-
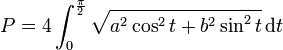
qui s'exprime sous forme de série, en notant e l'excentricité de l'ellipse (formule de J.H.Lambert(1772)):
-
![P = 2\pi a \left[{1 - \left({1\over 2}\right)^2e^2 - \left({1\cdot 3\over 2\cdot 4}\right)^2{e^4\over 3} - \left({1\cdot 3\cdot 5\over 2\cdot 4\cdot 6}\right)^2{e^6\over5} - \cdots}\right]](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/87be10004db90cdd3d8d01d679874e59.png) où
où
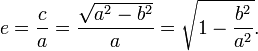
La difficulté de ces calculs a conduit à développer des approximations. La deuxième proposée, plus précise, est l'œuvre de Ramanujan :
-
![P \approx \pi\sqrt {2(a^2 + b^2)}\approx \pi \left[3(a+b) - \sqrt{(3a+b)(a+3b)}\right]](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/4ccbf3ea72ece2952**93234538d6340.png)
Courbe rectifiable
Le problème du calcul d'un périmètre est plus ardu si la frontière est courbe et non plus polygonale.
Il est toujours possible d'approcher la longueur d'une courbe par celle d'un polygone d'approximation. La longueur du polygone d'approximation est la somme des longueurs de ses côtés. Lorsque le pas, c'est-à-dire la longueur maximale entre deux sommets consécutifs du polygone, tend vers zéro, la limite supérieure de la longueur du polygone tend vers la longueur de la courbe. Si la longueur de la courbe est finie, celle-ci est dite rectifiable. Ce raisonnement permet de calculer des valeurs approchées de nombreuses courbes.
Une valeur exacte est possible lorsque la courbe est paramétrée par une fonction continûment dérivable. Alors la courbe est rectifiable. Si la courbe est un arc paramétré par une fonction f définie sur un intervalle [c;d], alors sa longueur est :
-
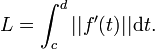
En particulier, si f(t) = (x(t) ; y(t)) et si les coordonnées s'expriment dans une base orthonormale, la longueur L de la courbe est donnée par :
-
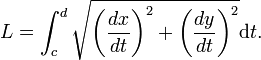
Cette formule permet d'établir celle donnée plus haut, pour le périmètre de l'ellipse ( x(t)=a cos t, y(t)=b sin t, I=]0, π/4[ ).
Il est également possible d'utiliser les coordonnées polaires (θ, r(θ)) où r est une fonction continûment dérivable de θ définie sur un intervalle [θ1;θ2]. Dans ce cas :
-
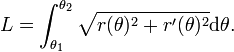
Courbes fractales
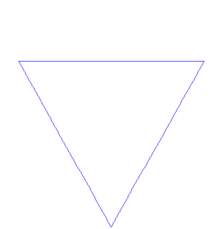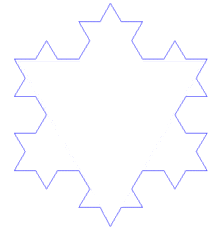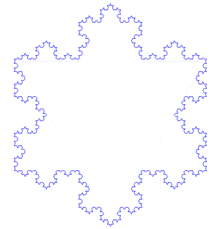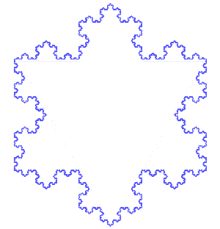
Construction du « flocon ».
Un exemple : Le flocon de von Koch
Le flocon de Koch est construit par une suite de polygones à la fois très simple et aux propriétés étonnantes.
On part d'un triangle équilatéral.
On partage chaque côté de la figure en trois segments de même longueur. On construit, sur chaque segment central et à l'extérieur de la figure précédente, un triangle équilatéral.
On répète le procédé de l'étape 2 indéfiniment.
À chaque itération, le polygone obtenu possède un périmètre égal à 4/3 de celui du précédent, la suite des périmètres obtenus tend vers l'infini. Pourtant, tous ces polygones sont inclus dans le cercle circonscrit au premier triangle, et ont une aire finie.
Fractales et dimension de Hausdorff
Si plusieurs surfaces ont des périmètres infinis, il est toutefois possible que certaines aient un « plus long périmètre » que d'autres. La dimension de Hausdorff introduite en 1918, permet de les comparer en étendant encore la notion de longueur, et donc celle de périmètre.
Fragments d'histoire
Aire et périmètre
Des plans tracés sur des tablettes d'argile et datant d'Ur III (fin du III millénaire av. J.‑C.) comportent des mentions de longueurs de terrains, qui sont découpés en triangles et quadrilatères afin de faciliter les calculs. Mais les aires de polygones, notamment les surfaces des champs, étaient calculées à partir des périmètres, même si certains scribes semblent s'être rendu compte que ces raisonnements pouvaient être faux. Cette façon de mesurer des villes ou des régions par leur périmètre est utilisée par Homère pour Troie ou encore par Hérodote :
« aussi donnait-on autrefois le nom d'Égypte à la Thébaïde, dont la circonférence est de six mille cent vingt stades. »
Dès 1800 av. J.-C., les problèmes de géométrie au sujet de périmètres sont attestés. Un problème classique trouvé sur de nombreuses tablettes consistait à trouver les dimensions d'un rectangle, connaissant son aire et son périmètre :
Exemple de problème babylonien — Un champ rectangulaire possède une aire de 96 et un périmètre de 40. Quelles sont les longueur et largeur du champ ?
La légende veut que Didon, vers 800 av. J.-C., cherchant une terre pour fonder une nouvelle cité pour son peuple, obtint d'un roi qu'il lui en cède « autant qu'il en pourrait tenir dans la peau d'un bœuf ». Didon découpa une peau de bœuf en très fines lanières et choisit une péninsule : avec les lanières, elle sépara la péninsule du continent et put ainsi délimiter un vaste terrain. Carthage était née. La légende de Didon peut avoir une origine didactique, car elle montre qu'aire et périmètre ne sont pas liés, elle est également une première approche du problème d'isopérimétrie.
La fondation de Rome est également une question de périmètre : Romulus trace, avec sa charrue, le périmètre circulaire de sa future ville. Le mot latin Urbs (la Ville, qui désigne Rome et a donné en français les mots urbain, urbaniser) serait une déformation d'une expression signifiant « tracer le périmètre ». Une racine indo-européenne signifiant pourtour, périmètre, clôture en serait à l'origine.
Le problème de l'isopérimétrie est très ancien, comme l'atteste la légende de Didon, et ses différentes réponses (polygone régulier, demi-disque dans un demi-plan, cercle) étaient connues dès l'antiquité grecque, bien qu'il ait fallu attendre le XIX siècle pour qu'une démonstration rigoureuse soit élaborée.
Circonférence du cercle
Les Babyloniens liaient l'aire A et le périmètre P d'un cercle suivant un algorithme de calcul équivalent à la formule ce qui donne une approximation de π égale à 3. Même lorsqu'ils connaissaient le diamètre d'un cercle, les scribes passaient toujours par le calcul de son périmètre (en multipliant le diamètre par 3) pour ensuite obtenir son aire. La dimension usuelle pour un cercle était toujours son périmètre, jamais son diamètre ni son rayon. Cela montre que, pour les anciens, un cercle était plutôt vu comme une circonférence plutôt que comme une courbe définie par un centre et un rayon. La procédure pour calculer l'aire d'un disque à partir de son diamètre était la suivante, utilisée, dans cet exemple, pour déterminer le volume d'une bûche cylindrique dont le diamètre était 1 + 2/3 :
Méthode babylonienne — Triple 1 + 2/3, le dessus de la bûche, et 5, la circonférence de la bûche, viendra. Prends le carré de 5 et 25 viendra. Multiplie 25 par 1/12, la constante, et 2 + 1/12, l'aire, viendra.
L'approximation de π par 3 est également utilisée dans la Bible :
« Il fit la mer de fonte. Elle avait dix coudées d’un bord à l’autre, une forme entièrement ronde, cinq coudées de hauteur, et une circonférence que mesurait un cordon de trente coudées. »
et le Talmud :
« Ce qui a trois palmes de tour est large d'une palme. »

Encadrement de cercles par des polygones réguliers. Archimède, pour ses calculs, utilisa des polygones réguliers à 6, 12, 24, 48 et 96 côtés.
Archimède énonça et démontra, dans son traité De la mesure du cercle :
Approximation de π par Archimède — Le quotient du périmètre de tout cercle par son diamètre est plus petit que  mais plus grand que
mais plus grand que 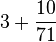 .
.
Ce qui donne un encadrement de π (qui est le quotient du périmètre de tout cercle par son diamètre). Pour parvenir à ce résultat, Archimède encadra le cercle par deux polygones réguliers dont il calcula les périmètres. Son résultat utilise des polygones réguliers à 96 côtés.
En 1424, Al-Kachi, dans son Traité sur le cercle, calcule une valeur approchée de π en encadrant le cercle entre deux polygones réguliers à 805 306 368 côtés avec seize décimales exactes. Son objectif était de déterminer une valeur approchée de π suffisamment précise pour pouvoir calculer non seulement la circonférence de la Terre, mais aussi celle de l'Univers. Son traité commence ainsi :
« Louange à Allah, qui connaît le rapport du diamètre à la circonférence [...] et paix à Mahomet, l'Élu, qui est le centre du cercle des prophètes. »
La méthode d'Archimède a été reprise en 1579 par François Viète et en 1593 par Adrien Romain pour calculer de douze à quinze décimales de π.
D'autres mathématiciens ont calculé des valeurs approchées de π en utilisant des calculs d'aires puis, à partir du XVII siècle, les techniques du calcul infinitésimal.
Longueur d'une courbe
La question du calcul de la longueur d'une courbe prend, au XVII siècle le nom de rectification d'une courbe. Elle est en général considérée comme impossible à résoudre, ce que Descartes exprime par : « ... la proportion qui est entre les droites et les courbes n'étant pas connue, et même je crois ne le pouvant être par les hommes. »
Au XVII siècle, l'invention du calcul infinitésimal a conduit à interpréter le calcul de la longueur d'une courbe comme celui d'une intégrale suivant la formule vue plus haut (voir l'exemple de l'ellipse).
Au XIX siècle, Camille Jordan donne une nouvelle définition de la longueur d'une courbe, se rapprochant de celle d'Archimède mais utilisant les outils modernes (dont le calcul de la limite d'une suite) : il approche la courbe par un polygone dont les sommets sont des points de cette courbe. Lorsque le nombre de ces points tend vers l'infini, la limite supérieure de la suite des longueurs des polygones obtenus, si elle est majorée, est la longueur de cette courbe. Cette définition de courbe rectifiable englobe et étend la précédente qui utilisait une intégrale.
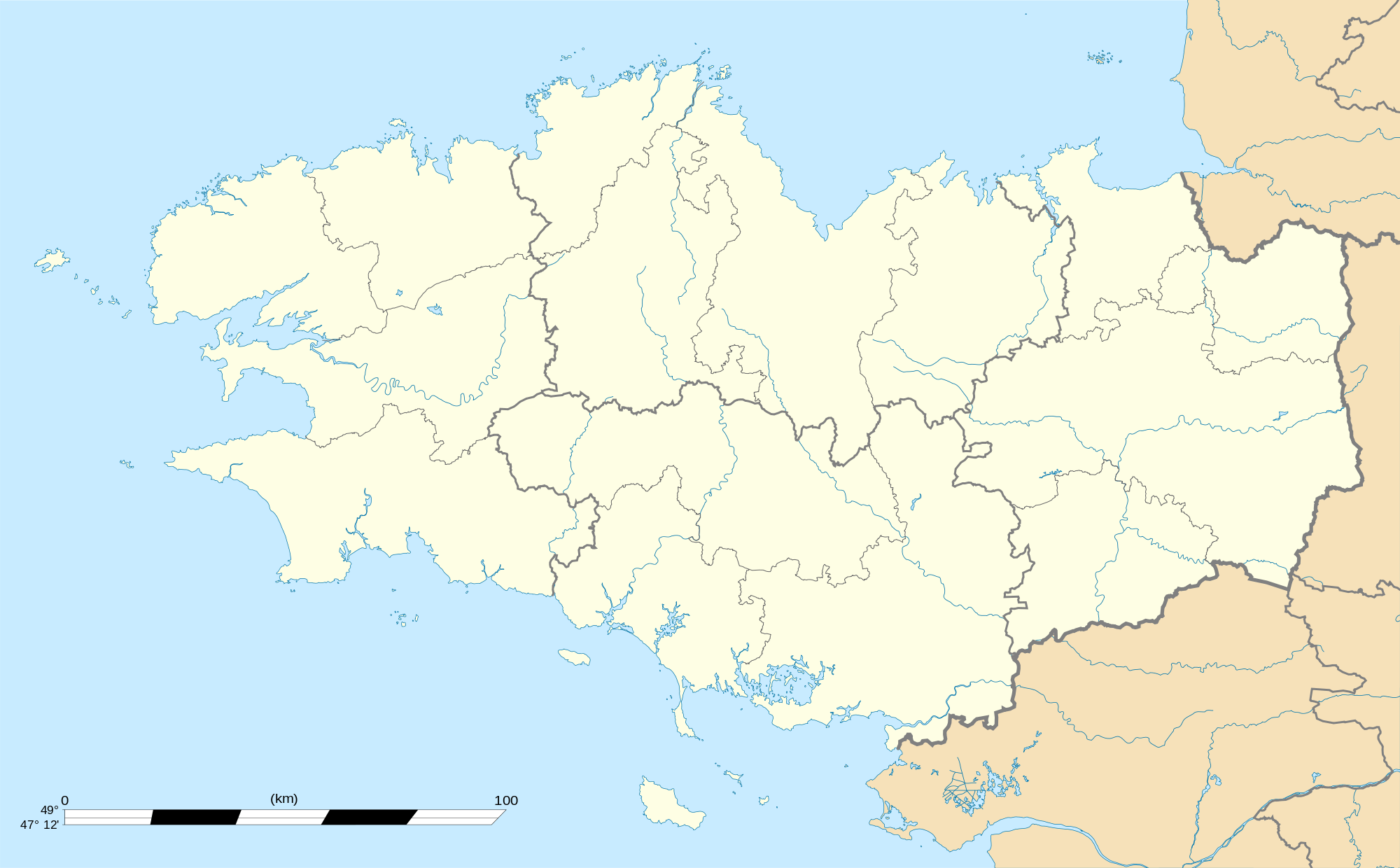
La côte bretonne.
Durant les XIX et XX siècles, des mathématiciens découvrent de nombreuses courbes « bizarres » comme celle de von Koch, qui ne sont pas rectifiables. À partir de 1967, Benoît Mandelbrot définit et étudie les fractales à partir d'une question apparemment très simple :
Question — Combien mesure la côte de la Bretagne ?
Mandelbrot explique que plus on cherchera à préciser la mesure, plus celle-ci sera grande, jusqu'à éventuellement devenir infinie. En effet, si on mesure grossièrement le périmètre de la Bretagne (ou de tout pays) sur une carte, on va obtenir un polygone. Mais plus la carte sera précise, plus le polygone sera découpé et donc son périmètre grandira. Si l'on veut le « vrai » périmètre de la Bretagne, il faudra aller sur place mesurer chaque caillou, chaque escarpement de rocher, voire chaque atome de ces composants. L'étude de ces objets dépasse le cadre du calcul de périmètres.

 词典释义:
词典释义:
 ,
,  边,
边,  长
长
 长
长 ,
,  围
围 围,四
围,四 ;
; 边地区
边地区 长, 湿
长, 湿


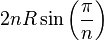 .
.



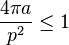

 .
.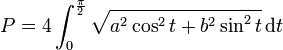
![P = 2\pi a \left[{1 - \left({1\over 2}\right)^2e^2 - \left({1\cdot 3\over 2\cdot 4}\right)^2{e^4\over 3} - \left({1\cdot 3\cdot 5\over 2\cdot 4\cdot 6}\right)^2{e^6\over5} - \cdots}\right]](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/87be10004db90cdd3d8d01d679874e59.png) où
où
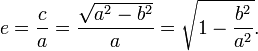
![P \approx \pi\sqrt {2(a^2 + b^2)}\approx \pi \left[3(a+b) - \sqrt{(3a+b)(a+3b)}\right]](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/4ccbf3ea72ece2952**93234538d6340.png)
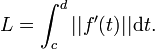
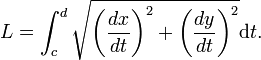
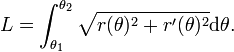


 mais plus grand que
mais plus grand que 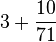 .
.