En mathématiques, et plus précisément en géométrie différentielle, on dit qu'une variété est feuilletée, ou munie d'un feuilletage, si elle se décompose en sous-variétés de même dimension, appelées feuilles, qui localement, s'empilent comme les sous-espaces ℝ × ℝ.
Définition
Formellement, un feuilletage sur est un atlas feuilleté, autrement dit une famille de cartes locales , où , et les changements de carte préservent cette décomposition : pour tout , .
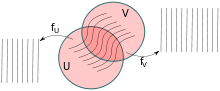
Quand une variété est feuilletée, dans chaque ouvert de carte, on appelle « feuille locale » d'un point l'ensemble des où . Comme les changements de cartes préservent les feuilles locales, on peut recoller les feuilles locales pour obtenir des feuilles (sous-entendu globales), qui sont des sous-variétés immergées, mais pas nécessairement plongées (elles peuvent être denses).
La régularité des cartes n'a pas été précisée. Il est fréquent de rencontrer en systèmes dynamiques des feuilletages qui sont seulement continus, ou alors hölderien. Ceci dit, en général, les feuilles elles-mêmes sont lisses, et c'est la famille des feuilles qui ne l'est pas.
Exemples
Fibration
Une fibration est un cas particulier de feuilletage. En général, si on a un feuilletage, on a des section locales, autrement dit des sous-variétés transverses aux feuilles locales dans un petit ouvert, et qui intersectent chaque feuille locale de cet ouvert. A priori il n'existe cependant pas de section globale, c'est-à-dire de sous variété de telle que est transverse à chaque feuille locale (transverse au feuilletage, donc) et coupe chaque feuille.
Une fibration est donc un feuilletage pour lequel il existe une section globale qui coupe chaque feuille exactement une fois.
Lemme de Frobenius
Considérons un champ de plans dans , autrement dit un sous-fibré vectoriel de . Si on suppose que pour tout champ de vecteurs et inclus dans , leur crochet est aussi contenu dans , alors le lemme de Frobenius nous assure que l'on peut écrire
où 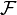 est un feuilletage de
est un feuilletage de 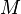 . Si
. Si 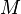 est
est 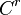 , alors
, alors 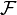 est lui aussi
est lui aussi 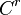 .
.
Dans le cas où 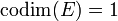 , donc
, donc 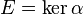 , cette condition dite « d'intégrabilité » se réécrit
, cette condition dite « d'intégrabilité » se réécrit
-
-
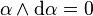 .
.
-
Ceci est un moyen classique d'obtention de feuilletages, et permet de traduire l'information contenue dans 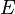 qui est dans l'espace tangent, en une information directement dans
qui est dans l'espace tangent, en une information directement dans 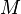 donc plus « topologique ».
donc plus « topologique ».
Feuilletages dynamiques
En dynamique hyperbolique, on suppose en général que l'on a des décompositions de l'espace tangent invariantes par la dynamique. La question de la régularité de ces décompositions est centrale dans ce domaine. le théorème qui fonde cette étude est le théorème des variétés stables . Sous certaines hypothèses, il nous assure que ces décompositions sont intégrables au sens du paragraphe précédent, et l'on dispose donc sur la variété de plusieurs feuilletages dynamiques.
Référence
Claude Godbillon, Feuilletages : études géométriques, Birkhäuser Verlag, coll. « Progress in mathematics », 1991, 474 p. (ISBN 3-7643-2638-7)
Portail de la géométrie
在数学上,叶状结构(foliation)研究几何的一个工具。非正式地说,一个叶状结构是一种给流形穿的条纹织物的衣服。在流形的每个足够小的片上,这些条纹给了流形一个局部乘积结构。这个乘积结构不用在局部区域之外一致(也就是不用有良定义的整体结构):沿着一个条纹走足够远可能回到一个不同的邻近的条纹。
定义
严格来讲,一个n维流形的维数为 p 的叶状结构是一个有如下映射的坐标卡组成的一个覆盖: 使得在交集上的变换函数 定义为 有以下形式 其中表示前个坐标,而表示后面p个坐标。在坐标卡上,条纹 常数和其他坐标卡上的条纹吻合. 技术上,这些条纹称为叶状结构的斑(plaques)。在每个坐标卡内,斑是维子流形。这些子流形从一个坐标卡到另一个坐标卡的拼起来就构成了最大连通子流形,称为叶状结构的叶(leaves).
例子
例1 维空间,可以分层为前n-p个坐标为常数的点组成的子空间的积。这可以用一个坐标卡来覆盖。 例2 如是流形之间的覆盖,而是上的叶状结构,则它拉回到上成为一个叶状结构。更一般的,如果一个映射只是有分支的覆盖,而分支轨迹和叶状结构交叉,则叶状结构可以被拉回(pull back)。 例3 若为李群,而通过将G的李代数的一个闭子代数指数化得到的子群,则 通过的陪集(coset)叶状化。
可积性
假设每个对象都是光滑的,叶状结构和矢量场有紧密的关系:给定一个矢量场在上,且处处不为0,其积分曲线给出一个1维叶状结构。(也就是余维n-1的叶状结构). 这个事实可以推广到Ferdinand Georg Frobenius(弗罗贝尼乌斯)的一个定理 (Frobenius定理), 它说一个分布(也就是,切丛的一个n-p维子丛)和一个叶状结构的叶相切的充分必要条件是和该分相切的矢量场的集合在李括号下封闭。也可以用不同的表达,把它作为切丛的结构群从到一个可归约子群的约化(reduction)。 Frobenius定理的条件象可积性条件一样;它断言如果那些条件满足归约可以发生因为满足所需的块结构的局部变换函数存在。 这是一个全局叶状结构理论,因为有拓扑约束存在。例如在曲面情况,一个处处非0的矢量场在可定向紧曲面上只有在曲面是环的情形存在。这是Poincaré-Hopf指标定理的结果,定理表明欧拉示性数在这种情况下必须为 0。

 词典释义:
词典释义:
 (做油酥点心用)
(做油酥点心用)
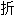
 ;
; 团;
团;