Une addition.
L'addition est une opération élémentaire, permettant notamment de décrire la réunion de quantités ou l'adjonction de grandeurs extensives de même nature, comme les longueurs, les aires, ou les volumes. En particulier en physique, l'addition de deux grandeurs ne peut s'effectuer numériquement que si ces grandeurs sont exprimées avec la même unité de mesure. Le résultat d'une addition est appelé une somme, et les nombres que l'on additionne, les termes.
En mathématiques, l'addition est développée sur les ensembles de nombres usuels mais se définit aussi pour d'autres objets mathématiques comme les vecteurs et les fonctions.
Par analogie, on appelle addition la loi de composition interne des espaces vectoriels et de certains groupes abéliens. D'autres structures mathématiques sont également munies d'opérations binaires appelées additions, mais qui ne satisfont pas toujours les propriétés de l'addition usuelle.
La Pascaline, première machine à calculer, ne pouvait effectuer que des additions.
Conception
Réunion de quantités
1 + 1 = 2.
Commutativité de l'addition.
L'addition se conçoit d'abord comme le dénombrement d'une réunion de collections d'objets, à trois conditions :
D'une part, ces objets ne doivent pas perdre leur individualité quand on les réunit, comme le feraient des liquides ou des boules de pâte à modeler.
D'autre part, les éléments « en double » apparaissant dans plusieurs collections à la fois doivent être considérés comme distincts et dénombrés individuellement.
Enfin, ces objets doivent être de même nature, c'est-à-dire répondre à une dénomination commune. Ainsi, pour additionner des pommes et des poires, il est nécessaire de les considérer globalement comme des fruits, afin d'exprimer le résultat en nombres de fruits.
Le résultat de l'addition est la quantité totale d'objets, qui peut se dénombrer soit par un comptage, soit par un calcul mathématique sur les nombres décrivant les quantités de départ.
De même, pour que l'addition puisse décrire la réunion d'objets fractionnaires, comme des portions de cercle ou des figures géométriques tracées sur un quadrillage, il faut que tous les objets soient évalués à partir d'une sous-division commune, une brique élémentaire. Mathématiquement, cette condition s'interprète comme la recherche d'un dénominateur commun à plusieurs fractions.
Certaines grandeurs physiques, mais aussi géométriques ou économiques, peuvent également s'additionner par la réunion des objets sur lesquels elles sont mesurées. Mais ces grandeurs doivent alors être évaluées relativement à une unité de mesure commune.
Bilan de variations
L'addition peut mettre en jeu des nombres négatifs en apparaissant comme le bilan des variations ou des déplacements successifs le long d'un axe orienté. Chaque terme est alors muni d'un signe indiquant son sens : positif pour un gain, une augmentation ou un déplacement dans le sens de l'axe ; négatif pour une perte, une diminution ou un déplacement dans le sens contraire à celui de l'axe. Le résultat de l'opération est alors appelé une « somme algébrique ».
Les variations peuvent là encore concerner des quantités entières ou fractionnaires, ou n'importe quelle grandeur mesurée.
Par exemple, l'addition de 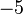 et
et 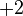 traduit une perte de cinq unités et le gain de deux unités. Le résultat de l'addition,
traduit une perte de cinq unités et le gain de deux unités. Le résultat de l'addition, 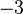 , correspond à la variation globale du nombre d'unités : trois unités ont été perdues.
, correspond à la variation globale du nombre d'unités : trois unités ont été perdues.
Cette conception peut être étendue pour définir l'addition des vecteurs par juxtaposition de déplacements ou translations, en n'imposant plus qu'ils se fassent le long d'un même axe.
Construction formelle
La formalisation mathématique des nombres entiers naturels privilégie cependant une définition ordinale de l'addition, par récurrence. Ainsi, partant de la seule opération « ajouter un », l'addition des nombres 3 et 2 se conçoit sous la forme « 3 auquel on ajoute un par deux fois » (3+1+1). Dans ce contexte, les propriétés de commutativité et d'associativité ne sont alors plus du tout évidentes et doivent être démontrées.
À partir de l'addition des entiers naturels, sont construites successivement les additions des entiers relatifs, des rationnels, des réels et des complexes. (Cet ordre ne reflète pas l'ordre chronologique avec lequel sont apparus ces ensembles de nombres.)
Opération numérique
Notation

Ancien symbole de l'addition
L'addition de deux termes et se note habituellement et se lit « plus », parfois « et » ou « ajouté à ». Le signe « + » remplace depuis la fin du XV siècle le symbole p pour « plus ».
Cette notation infixe peut être remplacée dans certains contextes par une notation fonctionnelle ou par une notation postfixée . Dans la décomposition arborescente d'une expression algébrique, l'addition est représentée par un nœud trivalent avec deux entrées et une sortie.
 |
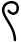 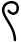
|
 |
   
|
   |
 |
   |
|
Le nombre 1527 en notation égyptienne
Dans un système de notation additive tel que le système unaire ou la numération égyptienne, le signe « + » n'a pas besoin d'être indiqué puisque l'écriture des nombres consiste déjà à décomposer les nombres en une somme de valeurs numériques fixées.
Dans un système de notation positionnelle telle la notation moderne, l'addition de plusieurs nombres est parfois représentée par la superposition des écritures de nombres, tous les chiffres d'une même position étant alignés verticalement. Cette disposition facilite le calcul manuel de la somme de plusieurs nombres.
Propriétés
L'addition de nombres possède certaines propriétés valables dans tous les ensembles de nombres usuels :
elle est commutative, c'est-à-dire que l'ordre dans lequel sont donnés les termes de l'addition n'a pas d'influence sur le résultat :
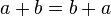 ;
;
elle est associative, c'est-à-dire qu'il n'y a pas besoin de préciser par des parenthèses l'ordre dans lequel est effectuée une suite d'additions :
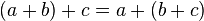 , d'où la notation sans parenthèses
, d'où la notation sans parenthèses  ;
;
elle est simplifiable, c'est-à-dire que dans une égalité d'additions, on peut supprimer deux termes identiques de part et d'autre du signe égal :
si 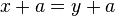 alors
alors 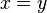 ;
;
l'élément nul ou zéro, noté 0, est neutre pour l'addition :
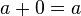 .
.
Chaque nombre  possède un symétrique pour l'addition, appelé « opposé » et noté
possède un symétrique pour l'addition, appelé « opposé » et noté 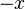 , c'est-à-dire tel que
, c'est-à-dire tel que 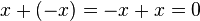 .
.
Les ensembles de nombres 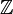 ,
, 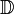 ,
, 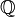 et
et 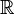 possèdent tous les opposés de leurs nombres, mais l'ensemble
possèdent tous les opposés de leurs nombres, mais l'ensemble 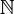 ne possède pas les opposés des nombres entiers strictement positifs.
ne possède pas les opposés des nombres entiers strictement positifs.
L'addition avec un symétrique permet de définir la soustraction par .
Procédé de calcul

Un abaque
L'évaluation du résultat d'une addition dépend du système de numération employé, c'est-à-dire de la manière de représenter les nombres.
Dans un système additif, il suffit de juxtaposer les écritures puis de simplifier l'expression en regroupant les symboles de même valeur pour en remplacer une partie par des symboles de valeur plus élevée lorsque c'est possible. De manière générale, les systèmes de numération non chiffrés ont pu développer une technique d'addition par la pratique de l'abaque.
| + |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 2 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 3 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 4 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
| 5 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
| 6 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 7 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| 8 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
| 9 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
| Table d'addition en écriture positionnelle décimale |
Dans un système de numération positionnelle chiffrée, le calcul d'une somme d'entiers passe par l'utilisation d'une table d'addition. Celle-ci permet de trouver la somme des chiffres sur chaque position.
L'écriture du résultat se fait de la position la plus basse à la position la plus haute (de droite à gauche en notation moderne). Pour chaque position, on inscrit le chiffre des unités de la somme des chiffres et on reporte une retenue sur la position suivante si cette somme est plus grande que la base. Chaque chiffre du résultat est ensuite incrémenté de l'éventuelle retenue.
Pour clarifier visuellement le procédé, on peut commencer par poser l'addition, c'est-à-dire, en notation moderne, écrire l'un en dessous de l'autre les nombres à additionner en alignant verticalement les positions correspondantes.
Cette méthode se généralise pour les nombres décimaux en alignant verticalement les virgules.
L'addition de fractions d'entiers passe par une mise au même dénominateur, puis une addition des numérateurs et enfin par une éventuelle simplification de la fraction obtenue.
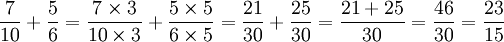
Quant à l'addition des fractions égyptiennes de numérateur unitaire et de dénominateurs tous distincts, elle fait appel à un processus itératif de simplification des fractions apparaissant en double.
Les sommes d'entiers, de décimaux et de rationnels peuvent toujours se ramener à une forme où ne figure plus le signe « + ». En revanche, une somme de réels n'admet pas toujours une telle forme : on ne peut pas simplifier l'écriture de 1 + √2.
Itération
En choisissant un terme constant , l'addition permet de définir une fonction que l'on peut itérer pour construire des suites arithmétiques de raison . De telles suites vérifient pour tout entier positif la relation . Elles s'écrivent alors sous la forme : .
Ces répétitions d'addition permettent de définir la multiplication par un nombre entier : .
L'addition d'une suite finie de nombres définie par une formule générale (par exemple, l'addition des entiers impairs de 1 à 99) utilise des procédés spécifiques qui quittent le domaine opératoire de l'addition. L'étude des suites et séries associées fournit des méthodes plus efficaces pour le calcul de telles sommes.
Culture populaire
L'addition donne aussi lieu à certains jeux. La mourre, par exemple, consiste à deviner la somme de deux petits nombres, que les deux adversaires donnent simultanément avec leurs doigts.
En poésie, elle est évoquée par la Page d'écriture de Jacques Prévert.
Constructions géométriques
Les nombres intervenant dans une addition représentent parfois des grandeurs géométriques : longueur d'un segment, mesure d'un angle (orienté ou non), aire d'une surface carrée. Dans chacun de ces cas, le calcul de la somme peut être illustré par une construction géométrique à la règle et au compas. Il existe aussi dans chaque cas une construction de la soustraction qui permet à partir de la grandeur somme et d'une des grandeurs de départ de trouver l'autre grandeur de départ.
Longueurs
Pour représenter la somme des longueurs de deux segments, il suffit de prolonger à la règle l'une de ces deux segments au-delà de l'une de ses extrémités, puis de tracer un cercle centré en cette extrémité et ayant pour rayon l'autre longueur. L'intersection du cercle avec le prolongement définit la nouvelle extrémité de la longueur prolongée.
Ce principe est fondamental pour définir ce qu'est un nombre constructible.
Angles géométriques
Étant donnés deux secteurs angulaires tracés dans le plan, il est possible de construire un secteur angulaire dont la mesure de l'angle soit la somme des mesures des angles donnés. Il suffit pour cela de tracer d'abord un triangle isocèle dont le sommet principal et ses côtés adjacents constituent l'un des secteurs angulaires, puis de construire un triangle isométrique de sommet principal à la pointe de l'autre secteur angulaire avec un côté adjacent en commun et l'autre côté à l'extérieur du secteur angulaire. Les deux côtés extérieurs délimitent alors l'angle somme.
En cas d'addition d'angles avec des mesures importantes, l'angle somme peut avoir une mesure de plus de 360°.
Cette procédure, appliquée aux angles d'un triangle, permet de vérifier que la somme des mesures de ces angles vaut bien 180°.
Angles orientés, angles de vecteurs
L'addition d'angles orientés se fait de manière analogue à celle des angles géométriques, à la différence que le premier côté du deuxième angle doit être superposé au deuxième côté du premier angle.
La construction peut alors se décrire en termes de transformations du plan. Si le premier angle orienté est déterminé par un couple de vecteurs représentés à partir de la même origine et d'extrémités respectives et , il suffit de construire l'image de par la rotation de centre et d'angle le second angle orienté. Les vecteurs de même origine et d'extrémités et définissent alors l'angle orienté somme.
En appliquant cette opération aux angles de vecteurs de la forme , où est un point du cercle trigonométrique, l'addition angulaire définit une opération sur les points du cercle qui correspond à la multiplication des nombres complexes de module 1.
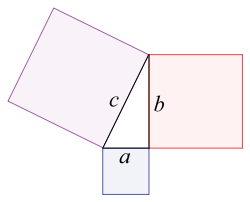
Addition des aires de carrés
Aires de surfaces carrées
Étant donné deux carrés tracés dans le plan, il est possible de construire un carré dont l'aire est la somme des aires des carrés initiaux. En effet, si les deux carrés initiaux peuvent être tracés de façon à avoir un sommet en commun et deux côtés perpendiculaires, le triangle formé par ces deux côtés est alors un triangle rectangle. Le théorème de Pythagore permet alors de montrer que le carré formé sur le troisième côté du triangle a pour aire la somme des aires des carrés initiaux.
L'opération ainsi définie sur les longueurs des côtés des carrés est l'addition pythagoricienne qui s'exprime (sur les couples de réels positifs) par :
-
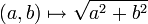 .
.
Ce problème de construction généralise celui de la duplication du carré, où les carrés initiaux ont la même dimension.
Construction universelle
En théorie des catégories, les entiers naturels forment un squelette de la catégorie des ensembles finis et l’addition et la somme, parce que l’addition est équivalent à la réunion disjointe. Dit informellement, la somme de deux entiers est l’objet minimal qui peut contenir toutes les deux indépendamment. Dans divers domaines des mathématiques, cette somme est un concept important, par exemple la somme directe en algèbre linéaire.
Extensions
D'autres structures mathématiques étendent certains ensembles de nombres et sont munis d'une opération binaire qui prolonge l'addition usuelle, mais qui ne possède pas toujours toutes ses propriétés.
Fonctions
Si les applications définies sur un ensemble donné commun et à valeur numérique peuvent s'additionner simplement composante par composante comme des vecteurs, il n'en est pas de même pour les fonctions qui ont un domaine de définition propre.
Étant donné deux fonctions et définies sur les domaines respectifs et (par exemple des intervalles réels), la fonction a pour domaine l'intersection et pour expression l'addition usuelle .
Cette addition est associative et commutative. Son neutre est la fonction définie partout et constamment nulle, mais l'addition d'une « fonction opposée » ne permet pas d'étendre le domaine de définition. Par exemple, la somme des fonctions et est la fonction nulle définie seulement sur les réels positifs.
Dans certains contextes, comme dans l'addition des fonctions méromorphes, l'effacement des singularités permet cependant d'évacuer le problème du domaine de définition de la somme.
Variables aléatoires indépendantes
En probabilités élémentaires, étant données deux variables aléatoires indépendantes ne pouvant prendre qu'un nombre fini de valeurs, l'addition se calcule en construisant un tableau avec une ligne par valeur de la première variable et une colonne par valeur de la seconde variable.
Chaque case du tableau est remplie avec d'une part la somme des valeurs de la ligne et de la colonne correspondante, d'autre part le produit des probabilités correspondantes. Ensuite, il suffit pour chaque valeur apparaissant dans le tableau de faire la somme des probabilités des cases qui la contiennent.
En probabilités continues, la densité de probabilité d'une somme de deux variables aléatoires indépendantes est donnée par le produit de convolution des densités de probabilités initiales. .
Cette présentation s'étend aux variables aléatoires dont la fonction de densité est une distribution.
Cette opération est associative et commutative. Le neutre est la variable aléatoire toujours nulle, mais seuls les nombres, représentés par les variables aléatoires constantes admettent des opposés. Il n'existe pas d'opposé aux variables aléatoires non constantes : elles sont d'étendue strictement positive, or l'étendue d'une somme est la somme des étendues.
Limites réelles
Les limites de suites ou de fonctions à valeur réelle peuvent être prises dans la droite continuée . L'addition des nombres peut alors s'étendre partiellement aux termes infinis. Pour tout réel :
-
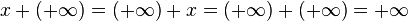 , et
, et
-
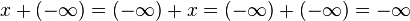 .
.
Cette opération garde des propriétés de commutativité et d'associativité mais n'est pas définie pour les couples 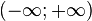 et
et  .
.
Selon les cas, la somme de deux suites ou fonctions admettant des limites infinies opposées peut avoir une limite finie, infinie ou pas de limite du tout.
Cette extension de l'addition est utilisée notamment en théorie de la mesure pour satisfaire l'additivité de la mesure sur des espaces de mesure infinie.
Ordinaux et ensembles ordonnés
La classe des ordinaux étend l'ensemble des entiers naturels par les nombres transfinis. L'addition s'étend ainsi en une opération sur les nombres ordinaux qui est associative mais non commutative. Par exemple, le premier ordinal infini, noté , vérifie la relation mais .
L'élément 0 reste neutre pour l'addition mais il n'y a pas d'ordinal négatif, bien que l'on puisse définir une différence entre deux ordinaux.
Cette opération s'étend aux ensembles ordonnés en général, l'addition de deux ensembles ordonnés et ayant pour résultat l'union disjointe dans lequel l'ordre des éléments est préservé à l'intérieur de chaque ensemble de départ et tous les éléments de sont inférieurs à tous les éléments de .
Nombres surréels
Un nombre surréel est une généralisation du concept de nombre sous la forme d'un couple d'ensembles s'écrivant , dans lequel chaque élément de l'ensemble de gauche est plus petit que tout élément de l'ensemble de droite.
L'addition se formule alors de manière récursive par
-
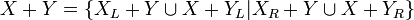
avec 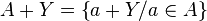 et
et 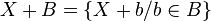 .
.
Autres additions
Addition vectorielle
Vecteurs d'un espace affine
Addition de deux vecteurs
Étant donnés quatre points , , , d'un espace affine tel que le plan ou l'espace euclidien, l'addition des deux vecteurs et se construit en définissant un point tel que (en traçant le parallélogramme ). Le vecteur somme s'identifie alors au vecteur .
L'addition de vecteurs satisfait toutes les propriétés de l'addition numérique. Son neutre est le vecteur nul et l'opposé d'un vecteur est un vecteur de même direction et même norme mais de sens opposé.
Lorsque les vecteurs sont définis sur une même droite munie d'un repère, l'addition des vecteurs s'identifie à celle des mesures algébriques.
Coordonnées et composantes
Les coordonnées des vecteurs dans un repère cartésien permettent de traduire l'addition vectorielle en une succession d'additions de nombres. En effet, si deux vecteurs du plan ont pour coordonnées respectives et , le vecteur somme aura pour coordonnées .
Dans l'espace usuel, l'addition est représentée par l'opération sur les triplets de coordonnées 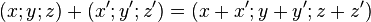 .
.
Le principe de l'addition terme à terme est repris pour d'autres structures mathématiques telles que l'ensemble des -uplets de nombres et les suites : .
Les matrices de même taille et les applications à valeur numérique s'additionnent également de cette manière.
Addition avec modulo
Addition modulo 5
| + |
0 |
1 |
2 |
3 |
4 |
| 0 |
0 |
1 |
2 |
3 |
4 |
| 1 |
1 |
2 |
3 |
4 |
0 |
| 2 |
2 |
3 |
4 |
0 |
1 |
| 3 |
3 |
4 |
0 |
1 |
2 |
| 4 |
4 |
0 |
1 |
2 |
3 |
Puisque la parité d'une somme ne dépend que de la parité des opérandes, il peut être défini une addition sur les parités.
| + |
pair |
impair |
| pair |
pair |
impair |
| impair |
impair |
pair |
Cette opération se généralise pour tout entier strictement positif en une addition modulo sur les chiffres de 0 à , dans laquelle chaque nombre est remplacé par le reste de sa division euclidienne par . L'addition sur les parités est alors représentée par l'addition modulo 2, où les nombres pairs sont remplacés par 0 et les nombres impairs par 1.
Addition booléenne
L'addition booléenne est l'écriture du connecteur logique « OU » avec les chiffres 0 pour FAUX et 1 pour VRAI. Elle est donc donnée par la table d'addition suivante :
L'opération est associative et commutative, l'élément 0 est neutre mais l'élément 1 n'a pas d'opposé.
Addition géométrique sur une courbe cubique
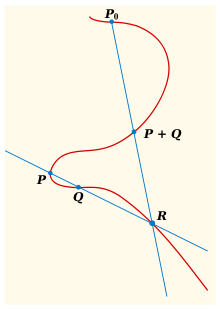
Addition de deux points d'une cubique, avec 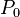 comme élément neutre fixé
comme élément neutre fixé
Sur certaines courbes, on peut définir une addition géométriquement. C'est possible en particulier sur des courbes cubiques, c'est-à-dire des courbes planes définies par une équation du 3 degré. Plus précisément, en appelant et les coordonnées dans le plan réel, les points de la courbe sont les points dont les coordonnées vérifient une équation , pour un polynôme du troisième degré à coefficients réels donné. On suppose aussi que la courbe n'a pas de points singuliers, c'est-à-dire ici de points de rebroussement ou de points doubles ; la tangente est donc bien définie en chaque point. Pour uniformiser les constructions, on rajoute aussi un point à l'infini.
Soient maintenant deux points quelconques de la courbe, 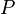 et
et  . La droite qui les joint recoupe la courbe en un troisième point
. La droite qui les joint recoupe la courbe en un troisième point 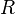 (si
(si 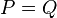 , on prend comme droite les joignant la tangente en
, on prend comme droite les joignant la tangente en 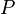 ). Ce procédé définit bien une opération binaire sur la courbe. Elle n'a pas encore les propriétés attendues d'une addition : par exemple, il n'y a pas d'élément neutre. Pour y remédier, on fixe un point au choix sur la courbe, qu'on note
). Ce procédé définit bien une opération binaire sur la courbe. Elle n'a pas encore les propriétés attendues d'une addition : par exemple, il n'y a pas d'élément neutre. Pour y remédier, on fixe un point au choix sur la courbe, qu'on note 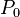 , et on considère la droite passant par
, et on considère la droite passant par 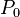 et
et 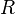 : elle coupe encore la cubique en un troisième point. C'est ce point qu'on appelle 'somme de
: elle coupe encore la cubique en un troisième point. C'est ce point qu'on appelle 'somme de 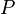 et
et  ' (et on le note
' (et on le note 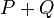 ).
).
Le point choisi 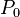 est l'élément neutre (le 'zéro') pour cette opération. Quant à l' 'opposé' d'un point
est l'élément neutre (le 'zéro') pour cette opération. Quant à l' 'opposé' d'un point 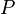 , c'est le troisième point d'intersection avec la courbe de la droite passant par
, c'est le troisième point d'intersection avec la courbe de la droite passant par 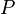 et
et  , où
, où  est le troisième point d'intersection avec la courbe de la tangente à la courbe en
est le troisième point d'intersection avec la courbe de la tangente à la courbe en 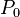 .
.

 词典释义:
词典释义:
 , 增添;
, 增添;  几行字
几行字 物, 添
物, 添 物;
物;  法;
法;  法
法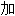 ,增多,倍增;
,增多,倍增;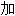 ;
;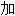 ,增大,增长;
,增大,增长;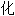
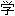 】
】
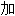 成 2. n. f. 【
成 2. n. f. 【
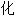
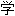 】
】
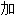 成反应 3. n. f. 【数
成反应 3. n. f. 【数
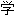 】
】
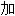 法 1. n. f 【石油】叠
法 1. n. f 【石油】叠
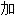 2. n. f. 【印】旁注
2. n. f. 【印】旁注
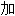 ;
; 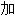 [法]; 结账; 买单; 添
[法]; 结账; 买单; 添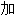 ; 相
; 相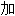 ; 账单
; 账单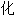
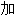 成
成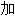 成
成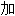 合金
合金 铜
铜
 剂
剂
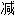 消元法
消元法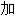 法交换律
法交换律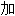 法消去律
法消去律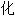
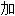 成
成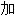 聚
聚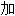 成反应
成反应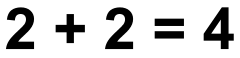
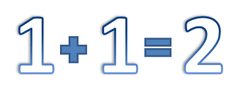

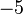 et
et 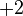 traduit une perte de cinq unités et le gain de deux unités. Le résultat de l'addition,
traduit une perte de cinq unités et le gain de deux unités. Le résultat de l'addition, 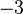 , correspond à la variation globale du nombre d'unités
, correspond à la variation globale du nombre d'unités
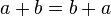 ;
;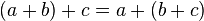 , d'où la notation sans parenthèses
, d'où la notation sans parenthèses  ;
;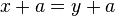 alors
alors 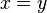 ;
;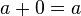 .
. possède un symétrique pour l'addition, appelé « opposé » et noté
possède un symétrique pour l'addition, appelé « opposé » et noté 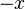 , c'est-à-dire tel que
, c'est-à-dire tel que 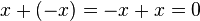 .
.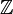 ,
, 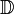 ,
, 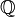 et
et 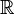 possèdent tous les opposés de leurs nombres, mais l'ensemble
possèdent tous les opposés de leurs nombres, mais l'ensemble 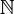 ne possède pas les opposés des nombres entiers strictement positifs.
ne possède pas les opposés des nombres entiers strictement positifs.

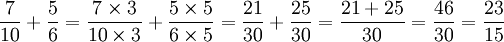

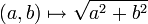 .
.
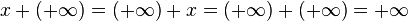 , et
, et
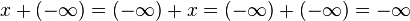 .
.
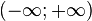 et
et  .
.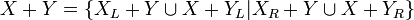
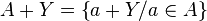 et
et 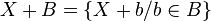 .
.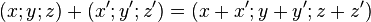 .
.
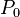 comme élément neutre fixé
comme élément neutre fixé
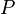 et
et  . La droite qui les joint recoupe la courbe en un troisième point
. La droite qui les joint recoupe la courbe en un troisième point 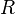 (si
(si 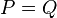 , on prend comme droite les joignant la tangente en
, on prend comme droite les joignant la tangente en 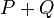 ).
). , où
, où 