En mathématiques, une fraction continue ou fraction continue simple ou plus rarement fraction continuée est une expression de la forme :
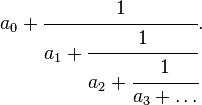
comportant un nombre fini ou infini d'étages.
On montre qu'on peut « représenter » — en un sens qui sera précisé — tout nombre réel sous forme d'une fraction continue, finie ou infinie, dans laquelle a0 est un entier relatif et les autres aj sont des entiers strictement positifs.
Comme dans la notation décimale usuelle, où chaque réel est approché par des nombres décimaux de plus en plus précisément au fur et à mesure de la donnée des décimales successives, de même chaque réel est approché par des fractions étagées de la forme ci-dessus de plus en plus précisément au fur et à mesure qu'on rajoute des étages. En outre, s'il faut une infinité de décimales pour décrire exactement un nombre non décimal, il faut un développement infini en fraction continue pour décrire exactement un nombre irrationnel.
Les fractions continues sont utiles en approximation diophantienne, notamment parce qu'elles fournissent, en un certain sens, les « meilleures » approximations des réels par des rationnels. Cette propriété est à l'origine d'algorithmes pour l'approximation de racines carrées, mais aussi de démonstrations d'irrationalité voire de transcendance pour certains nombres comme π ou e. La périodicité des fractions continues des racines carrées d'entiers strictement supérieurs à 1 et sans facteur carré a des conséquences utiles pour l'étude de l'équation de Pell-Fermat.
Déjà usitées chez les mathématiciens indiens au Moyen Âge, les fractions continues sont étudiées en Europe dès le XVII siècle et constituent encore un vaste sujet de recherche, près de 3 000 articles ont été publiés sur ce sujet au XX siècle. Elles sont maintenant généralisées à d'autres expressions, appliquées aux approximations de séries entières appelées approximant de Padé, ou encore adaptées aux applications linéaires.
John Wallis, à la suite des travaux de William Brouncker, utilise pour la première fois l'expression « fraction continue ».
Tour d'horizon
La notion de fraction continue est vaste et se retrouve dans de nombreuses branches des mathématiques. Les concepts associés peuvent être relativement simples comme l'algorithme d'Euclide, ou beaucoup plus subtils comme celui de fonction méromorphe.
Il est possible, dans un premier temps, de voir une fraction continue comme une suite d'entiers qui « représente » un réel. Cette situation est un peu la même que celle du système décimal qui représente π par la suite d'entiers 3, 1, 4, 1, 5, 9… Sous forme de fraction continue, la suite est 3, 7, 15, 1, 292, 1, 1… Un premier champ d'étude consiste à étudier la relation entre la suite 3, 7, 15, 1, 292, 1, 1… et celle des nombres rationnels que propose la fraction continue, en l'occurrence 3, 22/7, 333/106, etc., il permet de savoir comment passer de la première suite à la deuxième, comment la deuxième converge et répond à d'autres questions de cette nature. Tel est essentiellement l'objet de cet article.
Joseph-Louis Lagrange établit de manière rigoureuse les propriétés des fractions continues des entiers quadratiques.
Les fractions continues ont une relation particulière avec les racines carrées ou plus généralement les nombres, dits irrationnels quadratiques, de la forme a + b√d où a et b sont des nombres rationnels, b non nul, et d > 1 un entier sans facteur carré. Les fractions continues associées sont périodiques, à partir d'un certain rang, c'est-à-dire que la suite des entiers formant la fraction continue se répète à partir d'un certain rang et jusqu'à l'infini. Cette situation est à l'image des représentations décimales infinies de nombres rationnels. Ces fractions continues permettent de résoudre un célèbre problème d'arithmétique appelé équation de Pell-Fermat. Cette question fait l'objet de l'article Fraction continue d'un irrationnel quadratique.
À l'image du système décimal, la fraction continue offre des nombres rationnels de plus en plus approchés de leur cible. Ces approximations sont bien meilleures que celles décimales. La deuxième approximation décimale de π, égale à 31/10 possède un dénominateur relativement proche de celui de la deuxième approximation de la fraction continue 22/7, en revanche 22/7 est plus de 30 fois plus précis que 31/10. Ce type d'approche d'un nombre réel par un nombre rationnel est appelé approximation diophantienne. Les fractions continues y jouent un grand rôle. Elles ont permis de construire le premier nombre transcendant connu ou de montrer que le nombre e est irrationnel. À condition de généraliser la définition d'une fraction continue, il devient possible de montrer que π est aussi irrationnel — cette approche est traitée dans l'article Fraction continue et approximation diophantienne — puis, que e et π sont transcendants.
Une fraction continue ne concerne pas uniquement les nombres mais aussi les fonctions. On généralise encore plus les fractions continues en remplaçant les coefficients par des polynômes. Une motivation provient de l'analyse complexe, qui a pour objet l'étude des fonctions de la variable complexe à valeurs complexes, dérivables en tant que telles. L'approche classique consiste à les définir comme séries entières donc comme limites de polynômes. Une spécificité fréquente de ce type de fonction est de posséder des pôles. Si, au lieu d'approcher la fonction par des polynômes, on utilise des quotients, on construit une suite d'approximants de Padé qui ne possède pas nécessairement cette faiblesse.
D'autres propriétés ont été étudiées. À la différence du système décimal, un entier apparaissant dans une fraction continue n'est en général pas borné par 9, il peut devenir arbitrairement grand. Alexandre Khintchine s'est intéressé à la moyenne, au sens de limite des moyennes géométriques de tous ces dénominateurs. Pour presque tous les nombres, cette moyenne est la même (le mot « presque » possède ici le sens technique de la théorie de la mesure) ; cette moyenne est appelée constante de Khintchine.
Il est aussi possible de construire des développements en fractions en plaçant les barres de fraction sur le numérateur et non en-dessous : on obtient un développement en série de Engel :
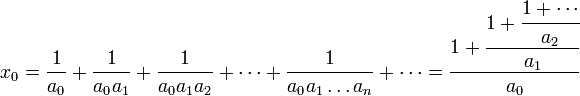 .
.
Repères chronologiques Âryabhata, un mathématicien indien, fait usage des fractions continues dès le V siècle. L'usage des fractions continues est ancien. Âryabhata (476-550), un mathématicien indien les utilise pour résoudre des équations diophantiennes ainsi que pour approximer précisément des nombres irrationnels. Brahmagupta (598-668) étudie plus en profondeur l'équation maintenant dite de Pell-Fermat. Il utilise une identité remarquable. Il cherche à résoudre l'équation x – 61y = 1 et trouve la plus petite solution : x = 1 766 319 049 et y = 226 153 980. Au XII siècle, la méthode est enrichie par Bhāskara II. Un algorithme, la méthode chakravala, analogue à celui des fractions continues, permet de résoudre le cas général. La différence la plus marquante avec la méthode européenne ultérieure est qu'il autorise les nombres négatifs dans la fraction, permettant une convergence plus rapide. L'apparition en Europe est plus tardive et italienne. Rafael Bombelli (1526-1572) fait usage d'un ancêtre des fractions continues pour le calcul d'approximations de la racine carrée de 13. Pietro Antonio Cataldi (1548-1626) comprend que la méthode de Bombelli s'applique pour toutes les racines carrées, il l'utilise pour la valeur 18 et écrit un petit opuscule à ce sujet. Il remarque que les approximations obtenues sont alternativement supérieures et inférieures à la racine carrée cherchée. Un progrès décisif a lieu en Angleterre. Le 3 janvier 1657, Pierre de Fermat défie les mathématiciens européens avec plusieurs questions dont l'équation déjà résolue par Brahmagupta. La réaction des anglais, piqués au vif, est rapide. William Brouncker (1620-1684) trouve la relation entre l'équation et la fraction continue, ainsi qu'une méthode algorithmique équivalente à celle des indiens pour le calcul de la solution. Il produit la première fraction continue généralisée, pour le nombre 4/π. Ces résultats sont publiés par John Wallis qui en profite pour démontrer les relations de récurrence utilisées par Brouncker et Bhāskara II. Il donne le nom de fraction continue dans la phrase : « Nempe si unitati adjungatur fractio, quae denominatorem habeat continue fractum ». À cette époque, Christian Huygens (1629-1695) découvre que les fractions continues sont l'outil idéal pour déterminer le nombre de dents que doivent contenir les roues des engrenages dans l'horlogerie. Il l'utilise pour la mise au point d'un automate planétaire. Henri Padé étudie en 1892 le cas des fractions continues construites à l'aide de polynômes. Quelques questions théoriques sont résolues au siècle suivant. L'usage montre que l'algorithme des fractions continues permet de résoudre l'équation de Pell-Fermat en utilisant le fait que la fraction est périodique à partir d'un certain rang. Leonhard Euler (1707-1783) montre que si un nombre possède une fraction continue périodique, alors il est solution d'une équation du second degré à coefficients entiers. La réciproque, plus subtile est l'œuvre de Joseph-Louis Lagrange (1736-1813). Durant ce siècle, Johann Heinrich Lambert (1728-1777) trouve une nouvelle utilité aux fractions continues. Il les utilise pour montrer l'irrationalité de π. Cet usage devient fréquent au XIX siècle. Évariste Galois (1811-1832) trouve la condition nécessaire et suffisante pour qu'une fraction continue soit immédiatement périodique. Joseph Liouville (1809-1882) utilise le développement en fraction continue généralisée pour exhiber des nombres non algébriques, c'est-à-dire transcendants. Ce sont les nombres de Liouville. En utilisant les fractions continues, Charles Hermite (1822-1901) prouve la transcendance de e, base du logarithme népérien en 1873. Grâce à lui, Ferdinand von Lindemann prouve en 1882 que π est transcendant, si bien que la quadrature du cercle est impossible à réaliser. À la fin du siècle Henri Padé (1863-1953) développe la théorie des approximants qui portent maintenant son nom et qui sont des fractions continues de polynômes. Cette technique est utilisée par Henri Poincaré (1854-1912) pour démontrer la statibilité du système solaire. Georg Cantor (1845-1918) prouve à l'aide des fractions continues que les points d'un segment et ceux situés à l'intérieur d'un carré sont en bijection. Les fonctions de cette nature sont étudiées dans le cadre de la théorie du chaos, elles sont discontinues sur chaque point rationnel de l'intervalle [0, 1].
Approche intuitive
De l'algorithme d'Euclide aux fractions continues
On commence par rappeler le déroulement de l'algorithme dû à Euclide de recherche du PGCD, en analysant l'exemple des deux nombres entiers 15 625 et 6 842. On procède à une suite de divisions euclidiennes avec reste :
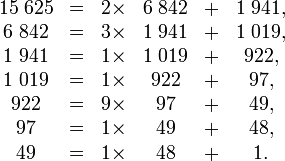
Une autre manière d'interpréter cet algorithme consiste à approcher par étapes le quotient 15 625 / 6 842. La partie entière de ce quotient est 2, ce qui permet d'écrire
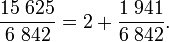
Que peut-on dire de la fraction 1 941 /6 842, à part qu'elle est plus petite que 1 ? Elle est comprise entre 1/4 et 1/3, son inverse, 6 842 / 1 941, possède comme partie entière : 3 ; et plus précisément, si l'on utilise les résultats de la deuxième division euclidienne :
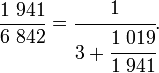
Ainsi de proche en proche :

qui est bien une fraction continue. On utilise parfois la notation suivante, plus commode :
![\frac{15\;625}{6\;842}=[2,3,1,1,9,1,1,48].](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/57f65fed6ac3be83b32cbf4f81bf0220.png)
On peut comparer 15 625 / 6 842 à ses réduites obtenues en tronquant successivement le nombre d'étages de la fraction continue. Le tableau suivant donne les troncatures en notation fractionnelle puis décimale, et la différence entre la réduite et le nombre 15 625 / 6 842.
Réduites successives de 15 625 / 6 842 et évolution de l'erreur
| Fraction |
Développement décimal |
Erreur |
|
2 |
2 |
–0,28... |
|
7/3 = 2 + 1/3 |
2,333... |
+0,049... |
|
9/4 = 2 + 1/(3 + 1/1) |
2,25 |
–0,033... |
|
16/7 |
2,285 7... |
+0,002 0... |
|
153/67 |
2,283 58... |
–0,000 10... |
|
169/74 |
2,283 783... |
+0,000 094... |
|
322/141 |
2,283 687 9... |
–0,000 001 0... |
|
15 625/6 842 |
2,283 688 979 83... |
0 |
La suite des erreurs est décroissante en valeur absolue et de signes alternés.
Développement en fraction continue d'un rationnel
Soit r = p/q un nombre rationnel (avec p et q entiers et q > 0). On cherche pour r un développement fini en fraction continue, c'est-à-dire une écriture de r sous la forme [a0, … , an] avec n entier naturel, a0 entier relatif et a1, … , an entiers > 0. On applique pour cela l'algorithme d'Euclide :
On pose p0 = p, p1 = q, et l'on construit les entiers a0 et p2 par division euclidienne :
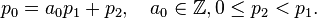
Puis, tant que pj n'est pas nul, on définit les entiers aj–1 et pj+1 par
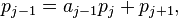
avec aj–1 entier au moins égal à 1 (pour j > 1) et 0 ≤ pj+1 < pj. L'algorithme d'Euclide s'arrête. On note n le plus grand entier pour lequel pn+1 n'est pas nul. On sait donc que pn/pn+1 est égal à l'entier an. On a alors :
![\frac{p_0}{p_1}=[a_0,a_1,\dots,a_n].](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/27cc2ef25ea075c38f95b8290d57dba5.png)
En effet :
![p_0/p_1=[a_0,p_1/p_2]=[a_0,a_1,p_2/p_3]=\dots=[a_0,a_1,\dots,a_n],](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/edad790519fee6df8c3794f2846f4638.png)
ou encore :
![p_n/p_{n+1}=[a_n]\text{ et pour }j=n-1,n-2,\ldots,0~:\quad p_j/p_{j+1}=[a_j,p_{j+1}/p_{j+2}]=[a_j,a_{j+1},\dots,a_n].](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/6bc07f625243a227556df0ca1c6799d7.png)
Représentation géométrique Un pavage d'un rectangle de longueur 30 et de largeur 13 permet de déterminer l'expression de 30/13 en fraction continue : 30/13=[2, 3, 4]. L'algorithme d'Euclide permet de calculer une fraction continue dans le cas des nombres rationnels. Cet algorithme admet dans ce cadre une interprétation géométrique. Soit r = p/q un nombre rationnel, on considère un rectangle de longueur p et de largeur q, et on le pave par des carrés de côté q. Si x est un entier, le pavage comporte exactement x carrés. Sinon, soit a0 le nombre de carrés insérés dans le rectangle, ou encore, le premier terme de la fraction continue. Il reste une bande non pavée de dimension q × b1 avec b1 égal à p – a0q ; on pave cette bande avec des carrés de dimension maximale, c'est-à-dire de côté x1. Le nombre de carrés est égal au deuxième terme a1 de la fraction continue. En réitérant la méthode, on obtient l'intégralité des coefficients ap. Dans l'image ci-contre, on pave le rectangle 30 × 13 par deux carrés de côtés 13. Il reste une bande de longueur 13 et de largeur 4. En termes de fraction continue, on obtient l'égalité : . La même démarche s'applique pour déterminer un rationnel connaissant sa fraction continue. [1, 1, 2, 3] = 17/10 Ensuite, on remarque qu'il est possible de remplir la bande restante de 3 carrés de côté 4 et il reste une bande de longueur 4 et de largeur 1, ce qui permet de terminer le calcul de la fraction continue : . La technique du pavage conduit à une fraction continue infinie si la longueur et la largeur du rectangle sont incommensurables. La même construction permet de trouver le rationnel dont on connait le développement en fraction continue. Dans l'image de gauche on peut retrouver le rationnel dont le développement est [1, 1, 2, 3]. Le dernier coefficient est égal à 3, on trouve donc 3 petits carrés de côté 1, qui donnent la taille du carré suivant (3). L'avant dernier coefficient 2 indique qu'il existe deux carrés moyens de côté 3. Ces deux côtés et le petit carré donnent la taille du carré plus grand (7). Le coefficient associé est égal à 1, il n'en n'existe donc qu'un unique de cette nature. Le carré plus grand (7) et le carré moyen (3) donnent le côté du dernier carré (10). Les deux derniers carrés donnent la longueur totale du rectangle (17). La fraction recherchée est égale à 17/10. Le processus s'arrête car p et q sont commensurables c'est-à-dire qu'il existe une longueur l et deux entiers a et b tels que p = la et q = lb. Considérons maintenant un rectangle de longueur L et de largeur l. Si le quotient L/l n'est pas rationnel, c'est-à-dire si les longueurs L et l sont incommensurables, le processus ne s'arrête pas. Tel est le cas pour la figure de droite représentant un rectangle d'or, c'est-à-dire un rectangle dont le rapport de la longueur sur la largeur est égal à φ le nombre d'or. On ne peut placer qu'un carré dans chaque bande ce qui amène à la représentation : . La suite des numérateurs et celle des dénominateurs sont de Fibonacci.
On a donc montré que pour tout rationnel r, l'algorithme d'Euclide fournit un développement fini en fraction continue de r (réciproquement, tout nombre qui possède un développement fini en fraction continue est évidemment rationnel). Le développement [a0, … , an] obtenu ainsi a la particularité que si n est non nul, alors an > 1. On en déduit un second développement : r = [a0, … , an – 1, 1]. Ce sont les deux seuls.
Quand on adjoint, au calcul des aj de ce développement, le calcul des numérateurs hj et dénominateurs kj des différentes réduites
![\frac{h_0}{k_0}=[a_0]=\frac{a_0}1,\quad \frac{h_1}{k_1}=[a_0,a_1]=a_0+\frac1{a_1}=\frac{a_0a_1+1}{a_1},\quad\ldots](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/8d167698fdbc31363fd55966cb915c44.png)
cet algorithme d'Euclide devient l'algorithme d'Euclide étendu. Plus précisément, la suite des couples d'entiers (ui, vi), fournie par l'algorithme étendu appliqué à (p, q), coïncide avec la suite des (kj, hj), aux signes près et à un décalage près des indices : kj = (–1)uj+2 et hj = (–1)vj+2. Pour tout j, les entiers kj et hj sont donc premiers entre eux et pj+1 = (–1)(qhj–1 – pkj–1). En particulier : la dernière réduite, hn/kn, est la fraction p/q mise sous forme irréductible et l'avant-dernière correspond à la solution particulière de l'identité de Bézout fournie par l'algorithme d'Euclide étendu : PGCD(p, q) = pn+1 = (–1)(qhn–1 – pkn–1).
Démonstration D'après le § « L'algorithme » de l'article sur l'algorithme d'Euclide étendu, les (ui, vi) sont définis par la relation de récurrence et l'initialisation D'après le § « Réduites d'une fraction continue » ci-dessous, les (kj, hj) suivent la relation de récurrence même en leur affectant les valeurs supplémentaires Le lien annoncé entre ces deux suites de couples d'entiers s'en déduit, par une récurrence d'ordre 2.
Développement en fraction continue du nombre π
Une remarque permet de généraliser la méthode précédente à un réel quelconque. Pour l'illustrer, appliquons-la sur le nombre π. La première étape, dans le cas d'un rationnel, était le calcul du quotient de la division euclidienne du numérateur par le dénominateur, ce qui ne fait plus sens pour un réel, en revanche le résultat était égal à la partie entière du rationnel, or la partie entière d'un réel a un sens. La partie fractionnaire, nécessairement plus petite que 1, était inversée, ce qui est encore possible ici. On obtient :
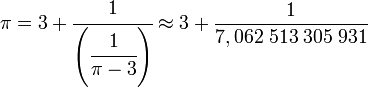 .
.
Comme π – 3 est plus petit que 1 (c'est une partie fractionnaire) son inverse est plus grand que 1, et n'est pas entier puisque π est irrationnel. On peut donc lui appliquer la même démarche :
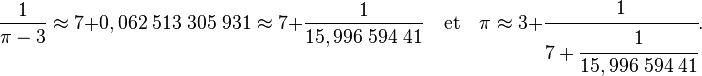
Le nouvelle valeur, approximativement égale à 15,997, est encore un irrationnel strictement supérieur à 1, d'où la possibilité d'une nouvelle étape, puis d'une nouvelle :

Puisque que π est irrationnel, le processus ne s'arrête jamais (en imaginant que le calcul est réalisé avec une infinité de décimales). On obtient comme suite de fractions 3 puis 22/7 ≈ 3,1428 puis 333/106 ≈ 3,14150 puis 355/113 ≈ 3,1415929 et enfin 103 993 / 33 102, proche de π avec une précision meilleure que le milliardième. Une fois encore, la suite des erreurs est décroissante en valeur absolue et de signes alternés.
Approche théorique
Notations et terminologie
Nous appelerons fraction continue ou fraction continue simple toute suite non vide (ap) dont le premier terme a0 est un entier relatif et tous les termes suivants sont des entiers strictement positifs.
L'ensemble de ses indices est soit de la forme {0, 1, … , n} pour un certain entier naturel n s'il s'agit d'une suite finie, soit égal à ℕ pour une suite infinie.
Sa réduite d'indice p est le rationnel [a0, a1, … , ap], défini par
Réduites d'une fraction continue
Soit (ap) une fraction continue. On lui associe deux suites d'entiers (hp) et (kp), définies par récurrence par :
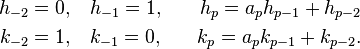
Alors, pour tout indice p de la fraction continue :
![\begin{matrix}[a_0,a_1,\ldots,a_p]=\frac{h_p}{k_p}&\quad&(1)\\
a_p=-\frac{h_pk_{p-2h_{p-2}k_p}{h_pk_{p-1h_{p-1}k_p}&&(2)\\
h_{p-1}k_p-h_pk_{p-1}=(-1)^p.&&(3)\end{matrix}](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/6c487ed8c494692be89f8bd0c037625a.png)
La propriété (3) montre, par application du théorème de Bézout, que les entiers hp et kp sont premiers entre eux.
Ces trois propriétés se démontrent directement par récurrence mais sont aussi des cas particuliers de celles des fractions continues généralisées, démontrées dans l'article correspondant. On y donne également une interprétation matricielle de la définition des hp et kp, dont résulte immédiatement, par transposition, une propriété duale de (1) :
![[a_p,a_{p-1},\ldots,a_0]=\frac{h_p}{h_{p-1}}\text{ (si }a_0>0\text{) et }[a_p,a_{p-1},\ldots,a_1]=\frac{k_p}{k_{p-1}}\text{ (si }p>0\text{).}](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/c66fee3bbb9bac0be69be53270a2e089.png)
Fraction continue d'un réel
Algorithme
Dans l'algorithme d'Euclide développé précédemment, l'entier aj est le quotient de pj dans la division euclidienne par pj+1. C'est donc la partie entière du réel xj égal à pj/pj+1. La partie fractionnaire xj – aj de xj est pj+2/pj+1, inverse du réel xj+1.
On peut alors définir un développement en fraction continue pour tout réel x. Le symbole ⌊s⌋ désigne la partie entière du nombre s. On pose :
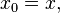
ainsi que la définition récurrente : tant que xj n'est pas entier,
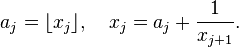
Si x est rationnel, comme on l'a vu plus haut, il existe un n tel que xn soit entier : on pose an = xn, l'algorithme s'arrête, et les deux suites (aj) et (xj) sont finies. Si x est irrationnel, l'algorithme ne s'arrête jamais et les deux suites sont infinies.
La suite (ap) est appelée la fraction continue du réel x.
Le réel xp (strictement supérieur à 1 si p > 0) est appelé le quotient complet de x d'indice p.
Sa partie entière ap est le quotient incomplet de x d'indice p.
On peut formaliser de manière plus informatique cet algorithme :
Donnée : un nombre x réel.
Initialisation : on assigne la valeur x à la variable X. La suite a est vide.
Boucle : On assigne à la variable A la partie entière de X, on concatène cette valeur à la suite a. Si X est entier, l'algorithme s'arrête. Si X n'est pas entier, on assigne à X la valeur de 1 /(X – A) et on recommence au début de la boucle.
Ou encore :
si x est entier, son développement est (x) ;
sinon, soit a0 sa partie entière ; le développement de x est : a0, suivi du développement de 1/(x – a0).
Si x est irrationnel, deux notations sont fréquemment utilisées dans ce contexte :
![x = a_0 + \cfrac 1{a_1 + \cfrac 1{a_2 + \cfrac 1{\cdots}}} = [a_0, a_1, a_2, \cdots].](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/74cf2a2506d94ab4ebadbb25af4ffb6c.png)
Elles seront légitimées plus loin : on verra entre autres que la suite des réduites converge vers x.
Quotients complets d'un réel
Soient x un réel, (ap) sa fraction continue, (hp) et (kp) les suites des numérateurs et dénominateurs des réduites associées à cette fraction continue, et (xp) la suite des quotients complets de x.
Pour tout indice p, on dispose de l'égalité :
![x = [a_0, a_1, \dots, a_{p-1}, x_p].](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/b0737ede38b9e050ffad3b77b2c2943a.png)
Or la démonstration des propriétés (1) et (2) ci-dessus des réduites d'une fraction continue reste valide si l'entier ap est remplacé par le réel xp. On obtient donc, respectivement :
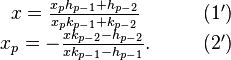
La propriété (2’) :
permet de calculer l'entier ap (partie entière de xp) en utilisant x comme seul réel, sans utiliser la suite de réels (xj), qui peut accumuler à chaque étape des imprécisions si l'algorithme est utilisé sur l'outil informatique et conduire ainsi à des valeurs erronées à partir d'un certain rang ;
montre que la suite des réels |kpx – hp| est strictement décroissante.
Encadrement et convergence
Montrons que toute fraction continue infinie (ap) « converge » — c'est-à-dire que la suite de ses réduites converge vers un réel x — et que (ap) est justement la fraction continue de x (qui est donc irrationnel). Ceci établira, pour tout irrationnel x, la convergence vers x de la fraction continue de x, et explicitera une bijection entre les irrationnels et les fractions continues infinies.
Soit donc (ap) une fraction continue infinie. La différence de deux de ses réduites successives,
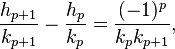
est alors le terme général d'une série alternée convergente. Par conséquent :
Les réduites de rangs pairs et impairs constituent deux suites adjacentes, dont la limite commune x vérifie, pour tout indice p :
Enfin, on peut démontrer que
La fraction continue de x est égale à (ap).
Encadrement de l'erreur d'indice p : La majoration est immédiate, et la minoration vient de
La fraction continue de x est égale à (ap) : La limite x est caractérisée par le fait qu'elle est strictement comprise entre [a0, … , ap] et [a0, … , ap+1], pour tout p. Notons (bj) sa fraction continue et montrons que bp = ap, par récurrence sur p. Soit p un entier naturel, supposons l'égalité acquise pour tous les indices < p (si p est nul, on ne suppose donc rien). Alors, x est strictement compris entre [b0, … , bp–1, ap] et [b0, … , bp–1, ap, ap+1]. Le p quotient complet xp de x est donc strictement compris entre ap et ap + 1/ap+1, si bien que la partie entière bp de xp est égale à ap.
Usages
Les usages des fractions continues sont nombreux. On trouvera par exemple dans Fraction continue et approximation diophantienne les preuves de l'irrationalité de e ou de π, dans Fraction continue d'un irrationnel quadratique un exemple de résolution d'équation de Pell-Fermat ou dans Approximant de Padé un prolongement analytique de la série entière de la fonction tangente. L'usage donné ici ne nécessite pour sa compréhension que les propriétés décrites dans cet article.
Automate planétaire
Christian Huygens construit un automate planétaire pour déterminer les positions relatives des corps célestes du système solaire.
Christian Huygens souhaite construire, à l'aide d'un mécanisme de type horlogerie un automate représentant le mouvement des planètes autour du soleil : « Ayant trouuè et fait executer depuis peu une machine automate qui represente les mouvements des Planetes dont la construction est d'une facon particuliere et assez simple a raison de son effect, au reste d'une grande utlitè a ceux qui estudient ou observent le cours des astres. » La difficulté à laquelle il est confronté est liée au rapport de la durée d'une année terrestre et de celle de Saturne. En un an, la Terre tourne de 359° 45' 40'' 30''' et Saturne de 12° 13' 34'' 18'''. Le rapport est égal à 77 708 431/2 **0 858. Combien faut-il de dents sur les deux engrenages supportant respectivement la Terre et Saturne ?
Huygens sait que les fractions continues offrent le meilleur compromis, ce qu'il exprime ainsi : « Or, lorsqu'on néglige à partir d'une fraction quelconque les derniers termes de la série et celles qui la suivent, et qu'on réduit les autres plus le nombre entier à un commun dénominateur, le rapport de ce dernier au numérateur sera voisin de celui du plus petit nombre donné au plus grand ; et la différence sera si faible qu'il serait impossible d'obtenir un meilleur accord avec des nombres plus petits. »
Un calcul en fraction continue montre que :
![\frac{77\,708\,431}{2\,**0\,858} = [29,2,2,1,5,1,4,1,1,2,1,6,1,10,2,2,3].](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/6f3ac1f32afb9c6194a**8d0fda87754.png)
On obtient la suite de fractions : 29/1, 59/2, 147/5, 206/7, 1 177/40 ... Les deux premières solutions ne sont guère précises, dans le premier cas, à la fin d'une rotation de Saturne, la position de la terre est fausse à près d'un demi-tour, dans l'autre cas l'erreur dépasse 4°. La cinquième est techniquement difficile, elle demande la fabrication d'une roue à plus de 1 000 dents ou plusieurs roues. La quatrième offre une précision proche de 3/1 000. C'est celle que choisit Huygens.
Si la terre fait cent tours complets, sur l'automate planétaire Saturne en fait 700/206, soit trois tours et un angle de 143° 18'. Dans la réalité, Saturne a tourné de 143° 26'. Soit une erreur de 8 minutes d'angle, largement inférieure aux imprécisions mécaniques de l'horloge. Un calcul analogue montre que la fraction 147/5 donne, dans le même contexte, une erreur supérieure à un degré, pour une mise en œuvre d'une difficulté technique comparable.
Fraction continue généralisée
Un calcul, dans la partie introductive de l'article, montre comment déterminer la fraction continue de π. Néanmoins, chaque étape est plus pénible car elle demande une précision sur la valeur initiale de plus en plus grande. Les séries entières, convergeant vers π, offrent bien une solution théorique pour le calcul de chaque coefficient de la fraction continue, mais il est calculatoirement trop inextricable pour être utilisable. Pour cette raison, il est plus simple d'obtenir une expression en fraction continue généralisée, en autorisant des numérateurs non nécessairement égaux à 1. La première fraction de ce type fut produite par Brouncker :
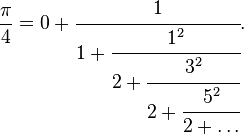
Une démonstration de cette égalité figure dans l'article « Formule de fraction continue d'Euler », par évaluation au point 1 d'une fraction continue généralisée de la fonction Arctangente. Ainsi, une fraction continue ne s'applique pas uniquement aux nombres, mais aussi à certaines fonctions.
Leonhard Euler calcule le premier développement en fraction continue généralisée d'une fonction.
Fraction continue de e
De même, Euler a développé la fonction exponentielle en une fraction continue de fonctions d'une forme appropriée : de manière à obtenir la fraction continue de e :
![{\rm e}=[2,1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,\ldots].](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/11fe9fd502b**b6078294d2248e55e79.png)

 词典释义:
词典释义:
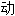
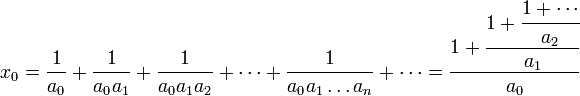 .
.
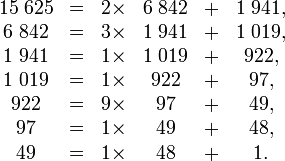
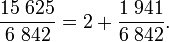
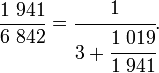

![\frac{15\;625}{6\;842}=[2,3,1,1,9,1,1,48].](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/57f65fed6ac3be83b32cbf4f81bf0220.png)
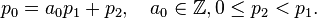
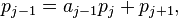
![\frac{p_0}{p_1}=[a_0,a_1,\dots,a_n].](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/27cc2ef25ea075c38f95b8290d57dba5.png)
![p_0/p_1=[a_0,p_1/p_2]=[a_0,a_1,p_2/p_3]=\dots=[a_0,a_1,\dots,a_n],](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/edad790519fee6df8c3794f2846f4638.png)
![p_n/p_{n+1}=[a_n]\text{ et pour }j=n-1,n-2,\ldots,0~:\quad p_j/p_{j+1}=[a_j,p_{j+1}/p_{j+2}]=[a_j,a_{j+1},\dots,a_n].](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/6bc07f625243a227556df0ca1c6799d7.png)
![\frac{h_0}{k_0}=[a_0]=\frac{a_0}1,\quad \frac{h_1}{k_1}=[a_0,a_1]=a_0+\frac1{a_1}=\frac{a_0a_1+1}{a_1},\quad\ldots](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/8d167698fdbc31363fd55966cb915c44.png)
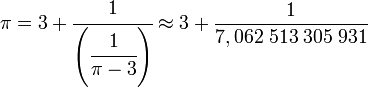 .
.
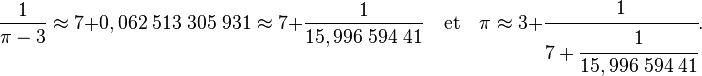

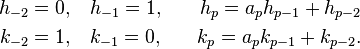
![\begin{matrix}[a_0,a_1,\ldots,a_p]=\frac{h_p}{k_p}&\quad&(1)\\
a_p=-\frac{h_pk_{p-2h_{p-2}k_p}{h_pk_{p-1h_{p-1}k_p}&&(2)\\
h_{p-1}k_p-h_pk_{p-1}=(-1)^p.&&(3)\end{matrix}](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/6c487ed8c494692be89f8bd0c037625a.png)
![[a_p,a_{p-1},\ldots,a_0]=\frac{h_p}{h_{p-1}}\text{ (si }a_0>0\text{) et }[a_p,a_{p-1},\ldots,a_1]=\frac{k_p}{k_{p-1}}\text{ (si }p>0\text{).}](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/c66fee3bbb9bac0be69be53270a2e089.png)
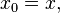
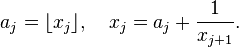
![x = a_0 + \cfrac 1{a_1 + \cfrac 1{a_2 + \cfrac 1{\cdots}}} = [a_0, a_1, a_2, \cdots].](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/74cf2a2506d94ab4ebadbb25af4ffb6c.png)
![x = [a_0, a_1, \dots, a_{p-1}, x_p].](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/b0737ede38b9e050ffad3b77b2c2943a.png)
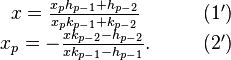
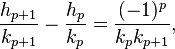

![\frac{77\,708\,431}{2\,**0\,858} = [29,2,2,1,5,1,4,1,1,2,1,6,1,10,2,2,3].](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/6f3ac1f32afb9c6194a**8d0fda87754.png)
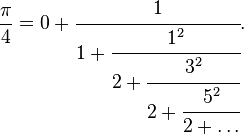
![{\rm e}=[2,1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,\ldots].](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/11fe9fd502b**b6078294d2248e55e79.png)
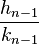 和
和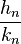 是连续的收敛,则如下形式的任何分数
是连续的收敛,则如下形式的任何分数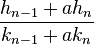
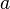 是非负整数,而分子和分母在
是非负整数,而分子和分母在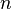 和
和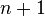 项(包含它们)之间,叫做“半收敛”、次收敛或中间分数。这个术语经常意味着排除了是收敛的可能性,而不是收敛是一种半收敛。
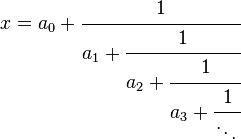
项(包含它们)之间,叫做“半收敛”、次收敛或中间分数。这个术语经常意味着排除了是收敛的可能性,而不是收敛是一种半收敛。 的连分数展开的半收敛包括了所有比有更小分母的任何逼近都好的有理数逼近。另一个有用的性质是连续的半收敛a/b和c/d有着
的连分数展开的半收敛包括了所有比有更小分母的任何逼近都好的有理数逼近。另一个有用的性质是连续的半收敛a/b和c/d有着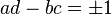 。
。