En mathématiques, dans la théorie des jeux combinatoires, les nimbers sont des jeux particuliers, définis comme des jeux de Nim à un tas avec un nombre éventuellement infini d'allumettes.
Plus précisément, le nimber correspondant au nombre ordinal , souvent noté *, est défini comme le tas d'allumettes du jeu de Nim avec un nombre d'allumettes. Un nimber peut aussi désigner directement ce nombre d'allumettes.
Les nimbers interviennent en particulier dans la théorie des jeux impartiaux : en effet, d'après le théorème de Sprague-Grundy, tout jeu impartial est équivalent à un certain nimber.
Jeu de Nim fini
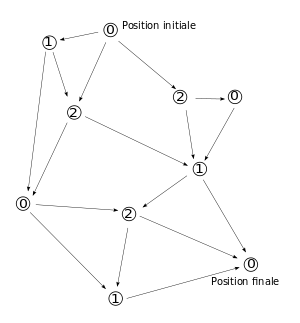
Le jeu représenté ci-dessus consiste à déplacer à tour de rôle un jeton depuis la position initiale jusqu'à la position finale, en suivant les flèches. On a indiqué pour chaque position le nimber correspondant. Les positions possédant un 0 sont les positions gagnantes à atteindre. La position initiale ayant un nimber nul est équivalente à un jeu de Nim à un tas vide. Celui qui commence a perdu.
Dans le cas d'un jeu de Nim fini où le perdant est celui qui ne peut plus jouer, on affecte à chaque position de ce jeu un nombre appelé nombre de Grundy ou nimber, défini récursivement comme suit :
Le nimber de la position finale vaut 0.
Le nimber d'une position donnée est le plus petit entier positif ou nul n'apparaissant pas dans la liste des nimbers des positions qui suivent immédiatement la position donnée.
Dans le jeu de Nim trivial à un seul tas, le nimber d'un unique tas de n allumettes n'est autre que n lui-même.
Les positions dont les nimbers valent 0 sont des positions gagnantes qu'il convient d'atteindre, les autres étant des positions perdantes. En effet, le joueur qui atteint une position ayant un nimber nul verra nécessairement son adversaire atteindre une position ayant un nimber non nul, quoique ce dernier joue, et lui-même aura un coup à jouer qui pourra le ramener à une position ayant un nimber nul. Il pourra donc se déplacer d'un nimber nul à un autre jusqu'à ce que son adversaire soit bloqué.
On généralise cette situation à des jeux infinis, à condition que, quelle que soit la position du jeu, il n'existe qu'un nombre fini de coups avant que la partie ne se termine. Cependant, chaque position peut avoir une infinité de successeurs immédiats. Dans ce cas, les nimbers peuvent prendre des valeurs infinies, qu'on dénote par des nombres ordinaux. Ces nimbers peuvent être dotés de propriétés intéressantes décrites ci-après.
Opération sur les nimbers
Il est possible de définir sur les nimbers des opérations d'addition et de multiplication, ce qui munit la classe des nimbers d'une structure de corps commutatif algébriquement clos de caractéristique 2. Cette construction théorique a été décrite en 1976 dans On Numbers and Games, par John Horton Conway.
Il est à noter que l'on parle en général de structure algébrique pour des ensembles. Cependant, les nimbers, de la même façon que les nombres ordinaux, ne forment pas un ensemble, mais une classe propre. On considère donc la structure, non pas de l'ensemble des nimbers, ce qui serait une expression incorrecte, mais de la classe des nimbers.
Opération d'addition
La définition des opérations sur les nimbers nécessite au préalable la fonction mex, dite de minimum exclu. Le mex d'un ensemble d'ordinaux est défini comme le plus petit ordinal n'appartenant pas à cet ensemble. Par exemple :
Mex(1, 2) = 0
Mex(0, 1, 5, 6) = 2
Mex(0, 1, 2, 3, ..., ω, ω+5) = ω+1
On utilise exactement la même définition du mex pour un ensemble de nimbers, à savoir que le mex d'un ensemble de nimbers est le plus petit nimber n'appartenant pas à cet ensemble. Dans le cas d'un jeu de Nim, le calcul du nimber d'une position donnée consiste exactement à prendre le mex de l'ensemble des nimbers des positions immédiatement postérieures.
L'opération d'addition de deux nimbers 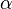 et
et 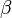 est définie comme suit :
est définie comme suit :
-
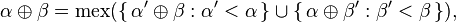
Selon le théorème de Sprague-Grundy, cette opération calcule le nimber de la position d'un jeu de Nim à deux tas (ou jeu de Marienbad) possédant respectivement et objets, chaque joueur choisissant l'un des deux tas à son gré pour retirer le nombre d'objets qu'il veut.
Structure de groupe abélien
L'opération d'addition définie sur les nimbers possède les propriétés remarquables suivantes :
le nimber 0 est un élément neutre :
commutativité :
associativté :
Tout nimber possède un opposé (lui-même) : et donc
Ces propriétés munissent la classe des nimbers d'une structure de groupe abélien. La dernière propriété exprime le fait que la position d'un jeu de Nim à deux tas constitué de deux tas égaux est une position gagnante : le premier joueur qui atteint une telle position joue ensuite symétriquement de son adversaire pour conserver toujours deux tas égaux jusqu'à ce qu'il ne reste plus aucun objet.
Opération de multiplication
Le produit de deux nimbers est défini comme suit :
Ce produit permet de calculer les nimbers des positions du produit 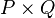 de deux jeux, défini comme suit:
de deux jeux, défini comme suit:
Une position du jeu produit est un ensemble dont les éléments (a, b) sont formés d'une position a du jeu P et d'une position b du jeu Q.
La position initiale du jeu produit est un ensemble dont les éléments (a, b) sont formés d'une position a initiale du jeu P et d'une position initiale b du jeu Q.
La position finale du jeu produit est un ensemble dont les éléments (a, b) sont formés d'une position a finale du jeu P ou d'une position finale b du jeu Q.
On passe d'une position à une autre en choisissant un élément (a, b) de la position dont on part et en le remplaçant par un triplet (a' , b), (a, b' ), (a' , b' ), où a' est une position de P qu'on peut atteindre à partir de a, et b' une position de Q qu'on peut atteindre à partir de b.
Le produit possède les propriétés suivantes :
le nimber 1 est un élément neutre :
commutativité :
associativité :
distributivité par rapport à l'addition :
Tout nimber non nul possède un inverse
Structure de corps
Addition et produit munissent la classe des nimbers d'une structure de corps commutatif.
La propriété la plus surprenante est le fait que tout nimber possède un inverse. Cela se démontre grâce à une formule explicite qui permet de construire l'inverse de façon inductive. On définit un ensemble S par induction :
si alors pour tout , on a :
On peut alors montrer que 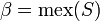 vérifie
vérifie 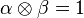 , c'est-à-dire
, c'est-à-dire 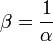 .
.
Sous-corps remarquables
Certains sous-ensembles de nimbers sont stables pour les opérations d'addition et de multiplication. Pour n > 0 donné :
l'ensemble des nimbers de 0 à est stable pour l'opération d'addition
l'ensemble des nimbers de 0 à est stable pour l'opération de multiplication
Il s'ensuit que l'ensemble des nimbers de 0 à est un corps fini à éléments distincts, donc isomorphe à .
Exemple du sous-corps fini F16
Pour illustrer les opérations d'addition et de multiplication, on peut donner les tables suivantes, qui montrent le résultat de l'addition et de la multiplication des nimbers compris entre 0 et 15. L'ensemble des nimbers de 0 à 15 est clos pour ces opérations, c'est-à-dire que le résultat est lui-même un nimber entre 0 et 15. On obtient ainsi une structure isomorphe au corps fini F16.
Table d'addition des Nimbers
| + |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 1 |
1 |
0 |
3 |
2 |
5 |
4 |
7 |
6 |
9 |
8 |
11 |
10 |
13 |
12 |
15 |
14 |
| 2 |
2 |
3 |
0 |
1 |
6 |
7 |
4 |
5 |
10 |
11 |
8 |
9 |
14 |
15 |
12 |
13 |
| 3 |
3 |
2 |
1 |
0 |
7 |
6 |
5 |
4 |
11 |
10 |
9 |
8 |
15 |
14 |
13 |
12 |
| 4 |
4 |
5 |
6 |
7 |
0 |
1 |
2 |
3 |
12 |
13 |
14 |
15 |
8 |
9 |
10 |
11 |
| 5 |
5 |
4 |
7 |
6 |
1 |
0 |
3 |
2 |
13 |
12 |
15 |
14 |
9 |
8 |
11 |
10 |
| 6 |
6 |
7 |
4 |
5 |
2 |
3 |
0 |
1 |
14 |
15 |
12 |
13 |
10 |
11 |
8 |
9 |
| 7 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
| 8 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 9 |
9 |
8 |
11 |
10 |
13 |
12 |
15 |
14 |
1 |
0 |
3 |
2 |
5 |
4 |
7 |
6 |
| 10 |
10 |
11 |
8 |
9 |
14 |
15 |
12 |
13 |
2 |
3 |
0 |
1 |
6 |
7 |
4 |
5 |
| 11 |
11 |
10 |
9 |
8 |
15 |
14 |
13 |
12 |
3 |
2 |
1 |
0 |
7 |
6 |
5 |
4 |
| 12 |
12 |
13 |
14 |
15 |
8 |
9 |
10 |
11 |
4 |
5 |
6 |
7 |
0 |
1 |
2 |
3 |
| 13 |
13 |
12 |
15 |
14 |
9 |
8 |
11 |
10 |
5 |
4 |
7 |
6 |
1 |
0 |
3 |
2 |
| 14 |
14 |
15 |
12 |
13 |
10 |
11 |
8 |
9 |
6 |
7 |
4 |
5 |
2 |
3 |
0 |
1 |
| 15 |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
Table de multiplication des Nimbers
| × |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 2 |
0 |
2 |
3 |
1 |
8 |
10 |
11 |
9 |
12 |
14 |
15 |
13 |
4 |
6 |
7 |
5 |
| 3 |
0 |
3 |
1 |
2 |
12 |
15 |
13 |
14 |
4 |
7 |
5 |
6 |
8 |
11 |
9 |
10 |
| 4 |
0 |
4 |
8 |
12 |
6 |
2 |
14 |
10 |
11 |
15 |
3 |
7 |
13 |
9 |
5 |
1 |
| 5 |
0 |
5 |
10 |
15 |
2 |
7 |
8 |
13 |
3 |
6 |
9 |
12 |
1 |
4 |
11 |
14 |
| 6 |
0 |
6 |
11 |
13 |
14 |
8 |
5 |
3 |
7 |
1 |
12 |
10 |
9 |
15 |
2 |
4 |
| 7 |
0 |
7 |
9 |
14 |
10 |
13 |
3 |
4 |
15 |
8 |
6 |
1 |
5 |
2 |
12 |
11 |
| 8 |
0 |
8 |
12 |
4 |
11 |
3 |
7 |
15 |
13 |
5 |
1 |
9 |
6 |
14 |
10 |
2 |
| 9 |
0 |
9 |
14 |
7 |
15 |
6 |
1 |
8 |
5 |
12 |
11 |
2 |
10 |
3 |
4 |
13 |
| 10 |
0 |
10 |
15 |
5 |
3 |
9 |
12 |
6 |
1 |
11 |
14 |
4 |
2 |
8 |
13 |
7 |
| 11 |
0 |
11 |
13 |
6 |
7 |
12 |
10 |
1 |
9 |
2 |
4 |
15 |
14 |
5 |
3 |
8 |
| 12 |
0 |
12 |
4 |
8 |
13 |
1 |
9 |
5 |
6 |
10 |
2 |
14 |
11 |
7 |
15 |
3 |
| 13 |
0 |
13 |
6 |
11 |
9 |
4 |
15 |
2 |
14 |
3 |
8 |
5 |
7 |
10 |
1 |
12 |
| 14 |
0 |
14 |
7 |
9 |
5 |
11 |
2 |
12 |
10 |
4 |
13 |
3 |
15 |
1 |
8 |
6 |
| 15 |
0 |
15 |
5 |
10 |
1 |
14 |
4 |
11 |
2 |
13 |
7 |
8 |
3 |
12 |
6 |
9 |
|

 词典释义:
词典释义:

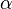 et
et 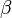 est définie comme suit
est définie comme suit 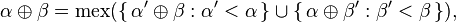
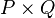 de deux jeux, défini comme suit:
de deux jeux, défini comme suit: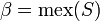 vérifie
vérifie 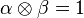 , c'est-à-dire
, c'est-à-dire 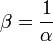 .
.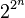 ),因此这个子集是封闭的。
),因此这个子集是封闭的。