Le déplacement d'une Dictyostelium discoideum dont la couleur du contour est fonction de la courbure. Échelle : 5 µm ; durée : 22 secondes.
Intuitivement, courbe s'oppose à droit : la courbure d'un objet géométrique est une mesure quantitative du caractère « plus ou moins courbé » de cet objet. Par exemple :
dans le plan euclidien, une ligne droite est un objet à une dimension de courbure nulle, et un cercle un objet de courbure constante positive ; dans l'espace euclidien usuel à trois dimensions, un plan est un objet à deux dimensions de courbure nulle, et une sphère un objet à deux dimensions de courbure constante positive. Une « selle de cheval » possède au contraire un point de courbure négative.
Cette notion intuitive de courbure se précise et admet une généralisation à des espaces de dimensions quelconques dans le cadre de la géométrie riemannienne.
Comme l'a montré Gauss pour le cas des surfaces (theorema egregium), il est très remarquable que la courbure d'un objet géométrique puisse être décrite de façon intrinsèque, c’est-à-dire sans référence aucune à un « espace de plongement » dans lequel se situerait l'objet considéré. Par exemple, le fait qu'une sphère ordinaire soit une surface à courbure positive constante est complètement indépendant du fait que nous voyons habituellement cette sphère comme étant plongée dans notre espace euclidien à trois dimensions. La courbure de cette sphère pourrait très bien être mesurée par des êtres intelligents bidimensionnels vivant sur la sphère (sortes de « fourmis bidimensionnelles »), à partir de mesures de longueurs et d'angles effectuées sur la sphère. La légende veut que Gauss se soit interrogé sur ces questions en étant confronté aux difficultés de cartographie de la Terre.
Courbure d'un arc
Tangente, cercle tangent (trait plein) et cercle osculateur (pointillé) en un point M de la courbe C
On peut définir la courbure d'un arc de l'espace euclidien à deux dimensions de plusieurs façons équivalentes. Il existe cependant deux conventions en usage, l'une faisant de la courbure une quantité obligatoirement positive, l'autre donnant une version algébrique de la courbure. Elle se calcule en chaque point de la courbe, moyennant certaines hypothèses sur les dérivées des fonctions servant à définir celle-ci.
La courbure quantité positive peut être vue comme la norme du vecteur accélération pour un mobile parcourant la courbe à vitesse constante égale à 1. C'est aussi l'inverse du rayon du cercle osculateur, cercle venant épouser la courbe au plus près au voisinage du point d'étude. En ce sens, la courbure indique la propension de la courbe à se comporter comme un cercle de plus ou moins grand rayon, c’est-à-dire à former un virage moins ou plus serré.
Pour introduire des versions algébrisées de la courbure, il faut munir le plan et la courbe d'une orientation et introduire un repère mobile (en) adapté au mouvement : le repère de Frenet. Le signe de la courbure s'interprète alors comme l'indication du sens dans lequel est tournée la concavité de la courbe. La courbure désigne aussi le taux (par unité d'abscisse curviligne) auquel les vecteurs du repère de Frenet tournent par rapport à une direction fixe.
La courbure peut ensuite être généralisée aux courbes gauches (courbes tracées dans l'espace à trois dimensions), mais les mêmes raisons qui empêchent d'orienter de façon compatible tous les plans de l'espace empêchent de définir une courbure algébrique ; elle est donc par convention toujours positive. La courbure s'accompagne alors d'un autre invariant, la torsion.
Le rayon de courbure est défini comme l'inverse de la courbure. La sinuosité décrit la courbure de plusieurs arcs reliés avec des points d'inflexion.
Courbure d'une surface de R
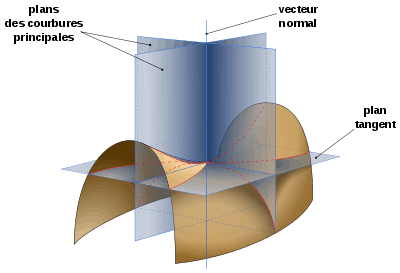
Illustration des courbures principales
Pour disposer de versions algébrisées de toutes les notions de courbure introduites, il convient de considérer une surface orientée.
Courbures principales
En un point M de la surface, on considère un plan tournant, perpendiculaire en M au plan tangent à la surface. Ce plan intersecte la surface considérée en une courbe. À chacune des courbes ainsi construite est associée sa courbure en M.
Les valeurs minimum et maximum de la courbure portent le nom de courbures principales. En général, elles sont différentes et, dans ce cas, les plans correspondant aux deux courbures principales sont perpendiculaires entre eux. Leur intersection avec le plan tangent définit les directions principales.
Courbures principales et directions principales sont respectivement les valeurs propres et vecteurs propres d'un endomorphisme symétrique du plan tangent. Ce dernier, l'endomorphisme de Weingarten, s'obtient à partir de la différentielle de l'application de Gauss.
Courbure moyenne
On appelle courbure moyenne 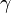 la moyenne des courbures principales, soit
la moyenne des courbures principales, soit 
Il s'agit de la demi-trace de l'endomorphisme de Weingarten.
Courbure de Gauss
On appelle courbure de Gauss 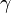 le produit des courbures principales, soit
le produit des courbures principales, soit 
Il s'agit du déterminant de l'endomorphisme de Weingarten.
Courbure totale
La courbure totale d'une surface orientée S de l'espace est l'intégrale de la courbure de Gauss sur la surface. Elle s'interprète également comme l'aire (algébrique) balayée par le vecteur normal unitaire sur la sphère unité.
Courbure d'une variété riemanienne
En géométrie riemannienne, la courbure est un tenseur introduit à partir de la notion de connexion. Cet objet s'est dégagé comme le plus pertinent, mais il peut être difficile à appréhender en raison du formalisme nécessaire à son introduction. La courbure sectionnelle d'une variété riemannienne, d'abord plus simple, véhicule autant d'information que le tenseur de courbure, et permet de faire le lien avec la courbure de Gauss.
Courbure sectionnelle
On définit une courbure sectionnelle pour chacun des 2-plans inclus dans chacun des espaces tangents d'une variété riemannienne. Si P est un tel plan en un point m, on considère en premier lieu la famille des géodésiques issues de m selon les vecteurs de P. Cette famille constitue une surface paramétrée incluse dans la variété, image du 2-plan par l'application exponentielle.
La courbure sectionnelle du 2-plan est alors la courbure de Gauss de cette surface. Formellement, la collection de toutes les courbures sectionnelles constitue une application sur la grassmannienne des 2-plans, à valeurs réelles.
Définition du tenseur de courbure
Soit une variété affine M de dimension , c'est-à-dire une variété munie d'une connexion affine . À partir de cette connexion, on définit le tenseur de courbure, ou tenseur de Riemann . Ce tenseur est défini pour X, Y et Z champs de vecteurs sur la variété par :
![\mathcal{R}(X,Y)Z \ = \ \nabla_X\nabla_Y Z \ - \ \nabla_Y\nabla_X Z \ - \ \nabla_{[X,Y]}Z](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/77354910451304b3f842f5e4c46098d0.png) ,
,
où [X, Y] est le crochet de Lie de X et Y. est un champ d'endomorphisme de l'espace fibré tangent TM : à tout champ de vecteur Z, il associe un nouveau champ de vecteur noté R(X, Y)Z.
Introduction d'une métrique
On munit la variété affine M d'un tenseur métrique g : est alors une variété riemannienne, et on peut définir une courbure à valeurs réelles par :
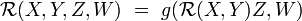 .
.
En composantes dans une base locale 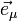 ,
, 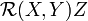 est le vecteur qui s'écrit :
est le vecteur qui s'écrit :
 .
.
où les  sont les composantes du tenseur de courbure. On a alors :
sont les composantes du tenseur de courbure. On a alors :
 .
.
En prenant sa trace (par rapport à X et Y), on obtient le tenseur de courbure de Ricci, et en prenant la trace de celui-ci, on obtient la courbure scalaire (qui est une fonction de M dans 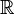 ).
).
Courbure scalaire, ou courbure de Ricci
Exemples
Pour l'espace euclidien, la courbure scalaire est nulle.
Pour la sphère de dimension rayon un, la courbure scalaire vaut .

 词典释义:
词典释义:

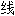 ,
,

 ;
; ;
;
 ,
, 大;
大;
 的;
的; ; 弯曲; 弯
; 弯曲; 弯 屈光不正
屈光不正 曲
曲 )
)
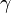 la moyenne des courbures principales, soit
la moyenne des courbures principales, soit 

![\mathcal{R}(X,Y)Z \ = \ \nabla_X\nabla_Y Z \ - \ \nabla_Y\nabla_X Z \ - \ \nabla_{[X,Y]}Z](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/77354910451304b3f842f5e4c46098d0.png) ,
,
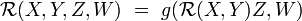 .
.
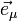 ,
, 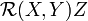 est le vecteur qui s'écrit
est le vecteur qui s'écrit .
.
 sont les composantes du tenseur de courbure. On a alors
sont les composantes du tenseur de courbure. On a alors .
.
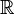 ).
). 其曲率为
其曲率为