L’automatique est une science qui traite de la modélisation, de l’analyse, de l’identification et de la commande des systèmes dynamiques. Elle inclut la cybernétique au sens étymologique du terme, et a pour fondements théoriques les mathématiques, la théorie du signal et l’informatique théorique. L’automatique permet de contrôler un système en respectant un cahier des charges (rapidité, précision, stabilité…).
Les professionnels en automatique se nomment automaticiens. Les objets que l’automatique permet de concevoir pour procéder à l'automatisation d'un système (automates, régulateurs, etc.) s'appellent les automatismes ou les organes de contrôle-commande d'un système piloté.
Un exemple simple d'automatisme est celui du régulateur de vitesse d’une automobile: il permet de maintenir le véhicule à une vitesse constante prédéterminée par le conducteur, indépendamment des perturbations (pente de la route, résistance du vent, etc.). James Clerk Maxwell, dans son article « On Governors » (1868), définissait ainsi le système de régulation qu'il avait inventé: « A governor is a part of a machine by means of which the velocity of the machine is kept nearly uniform, notwithstanding variations in the driving-power or the resistance ». Cette définition est une excellente introduction à l'automatique.
Histoire de l'automatique
Préhistoire de l'automatique
On peut faire remonter les débuts de l’automatique à l’Antiquité. Par exemple, les Romains régulaient le niveau d’eau des aqueducs grâce à un système de valves. Au XVI siècle, Cornelis Drebbel a conçu l'asservissement de température d'un four en combinant des effets thermiques et mécaniques ; alchimiste, Drebbel espérait grâce à ce four (« l'athanor ») transformer le plomb en or. Puis, au XVII siècle, Robert Hooke et Christian Huygens conçurent des régulateurs de vitesse (pour les moulins à vent en ce qui concerne Huyghens). En 1769 James Watt a conçu son fameux régulateur à boules pour la régulation de vitesse des machines à vapeurs. Parmi d’autres pionniers de l’automatique, il convient d’évoquer l’astronome Airy (vers 1840), James Clerk Maxwell (son article On governors, déjà mentionné, est le premier article mathématique sur la théorie du contrôle), Ivan Alexeïevitch Vichnegradski (1876) ; et, bien entendu, les mathématiciens Adolf Hurwitz et Edward Routh (auteurs du critère de stabilité qui porte leur nom, datant de la fin du XIX siècle), ainsi que les Français Liénard et Chipart, qui ont amélioré en 1914 le Critère de Routh-Hurwitz. On peut citer aussi Alexandre Liapounov, qui a présenté en 1892 sa thèse fondamentale sur la stabilité des équations différentielles, ainsi que tous les mathématiciens qui ont contribué à la théorie de la stabilité (voir l'histoire de la théorie de la stabilité). Ces derniers travaux, qui mènent à une époque assez récente, sont néanmoins à caractère essentiellement mathématique.
L'automatique fréquentielle
L’histoire de l’automatique proprement dite commence avec les fameux chercheurs des laboratoires Bell (fondés en 1925): Harold Stephen Black et Nathaniel Nichols (en), qui ont conçu leur célèbre diagramme, Harry Nyquist qui, le premier sans doute, a compris le problème de stabilité que posent les systèmes bouclés, enfin et surtout Hendrik Wade Bode. Ce dernier est très connu par son diagramme, mais son œuvre maîtresse est son livre Network Analysis and Feedback Amplifier Designer, édité juste après la seconde guerre mondiale (et réédité depuis), qui marque la maturité de l’automatique fréquentielle.
Les systèmes échantillonnés
Il faut mentionner aussi les pionniers de l’automatique à temps discret : l’Américain Claude Shannon, lui aussi chercheur aux laboratoires Bell, le Russe Yakov Zalmanovitch Tsypkin, l'Américain Eliahu Jury (en) enfin, auteur du critère correspondant à celui de Routh-Hurwitz mais pour les systèmes à temps discret. Une découverte fondamentale est le théorème de l'échantillonnage, attribué par de nombreux auteurs à Nyquist et Shannon, mais auquel il faut aussi associer, entre autres Edmund Taylor Whittaker et Vladimir Kotelnikov (en).
La commande optimale
Dans les années 1950, d’autres approches de l’automatique se préparent : en Russie avec Lev Pontryagin et ses collaborateurs, aux États-Unis avec Richard Bellman. Pontryagin conçoit le Principe du Maximum pour la commande optimale. Il s’agit d’une extension du Calcul des variations, avec « variations fortes » qui permettent d’obtenir une condition de maximum à la place de l’égalité d’Euler. Bellman invente la programmation dynamique, d’où il déduit l’équation d’Hamilton-Jacobi-Bellman (en), généralisation de l’équation d’Hamilton-Jacobi du Calcul des variations.
La représentation d'état
Les découvertes qui viennent d’être évoquées jouent bien sûr un rôle essentiel dans la théorie de la commande optimale, mais elles ont également conduit à la notion de représentation d’état. C’est Rudolf Kalman qui, en 1960, a fait la théorie (presque) complète de ces systèmes dans le cas linéaire. Il a notamment mis en évidence les notions fondamentales de commandabilité et d’observabilité. La même année (son "annus mirabilis"), il faisait la théorie de la commande optimale linéaire quadratique (par application des résultats de Pontryagin et de Bellman) et sa « version duale », le filtre de Kalman qui généralise le filtre de Wiener. Puis quelques mathématiciens, dont Harold J. Kushner (en), développent la commande optimale stochastique.
Applications de l'algèbre et de la géométrie différentielle
S’ouvre alors une nouvelle ère de l’automatique, avec des travaux de nature algébrique (pour les systèmes linéaires) ou relevant de la géométrie différentielle (dans le cas des systèmes non linéaires). Pour ce qui concerne les systèmes linéaires, un livre célèbre de W. M. Wonham (de), dont la première édition date de 1974 (mais qui a été plusieurs fois réédité), marque l’apogée de cette période. Concernant les systèmes non linéaires, un livre d'Alberto Isidori (en), dont la première édition date de 1985, puis plusieurs fois réédité et augmenté, a eu une influence considérable.
La robustesse
Bien que la notion de robustesse ait été prise en compte dans des approches fréquentielles traditionnelles, telles que la « théorie quantitative du bouclage (en) » développée par Isaac Horowitz dès 1963, c'est vers la fin des années 1970 que la problématique de la commande robuste, qui était complètement occultée dans une approche uniquement algébrique, est apparue comme incontournable. La commande optimale « linéaire quadratique » a des propriétés de robustesse intrinsèques (marge de phase d'au moins 60°, etc.), du moins dans le cas des systèmes monovariables, comme il résulte d'un article publié par Kalman dès 19**. La question s'est donc posée de savoir si cette propriété se conserve en présence d'un observateur. Or en 1978, John Doyle (en), un des pionniers de la théorie de la robustesse, a montré qu’une commande linéaire quadratique gaussienne (LQG) (dont l'observateur est un filtre de Kalman) peut n’avoir aucune propriété de robustesse. Le formalisme H-infini, établi par le mathématicien Godfrey Harold Hardy dès le début du XX siècle, mais introduit en 1981 par George Zames (en) dans le domaine de l'automatique, s’est avéré utile pour formaliser les problèmes de commande robuste. Il a été rapidement associé à des techniques d’optimisation convexe fondées sur des « inégalités matricielles linéaires » (LMI) qui ont pu conduire à des méthodes de synthèse (parfois excessivement) complexes.
Applications de l'analyse algébrique et de l'algèbre différentielle
Enfin, depuis le début des années 1990 se développe une nouvelle approche de l’automatique linéaire fondée sur la théorie des modules (plus précisément, des D-modules (en)) et l’analyse algébrique (en) (branche des mathématiques fondée sur les idées d'Alexandre Grothendieck, puis développée par Mikio Satō, Masaki Kashiwara (en) et, pour ce qui concerne les systèmes d'équations différentielles, Bernard Malgrange). On peut évoquer ici l’approche « behaviorale » de Jan C. Willems (en), ainsi que les travaux de Michel Fliess (qui a également appliqué aux systèmes non linéaires des méthodes issues de l'algèbre différentielle et est à l'origine, avec trois autres automaticiens, de la notion de « système plat »), d’Ulrich Oberst, ainsi que de leurs divers collaborateurs et émules.
Généralités, concepts
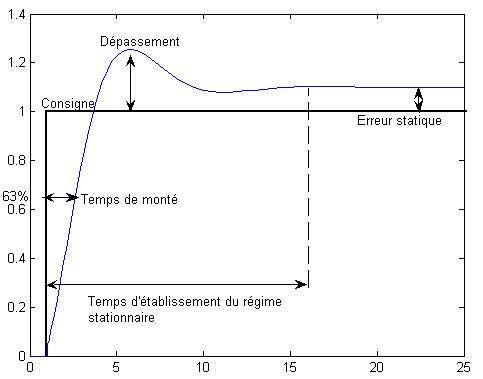
Consigne (en noir) et réponse (en bleu) d’un système asservi avec un régulateur PID
On souhaite contrôler la température d’un four. La première tâche consiste à définir le système « four ». Celui-ci possède une entrée (le courant fourni à la résistance de chauffage) et une sortie (la température à l’intérieur du four). On modélise le système sous forme d’équations, qui permettent d’exprimer les relations entre les entrées et les sorties du système, sous la forme d’une équation différentielle ou d’une fonction de transfert. On détermine aussi les conditions de stabilité du système (on ne veut pas que le four se mette à augmenter la température sans s’arrêter).
Les personnes chargées de réguler ce système ont un cahier des charges à respecter:
la stabilité (le régulateur ne doit pas rendre le système instable),
la poursuite (la température du four doit atteindre la température en consigne, on peut spécifier dans le cahier des charges si on a des contraintes de rapidité ou de dépassement),
le rejet des perturbations (on ouvre la porte du four, la température descend, la température doit rejoindre la température voulue).
Les coûts et délais de développement.
Après avoir déterminé la solution répondant le mieux aux besoins, on va synthétiser un nouveau système, le « régulateur » ; celui-ci aura pour entrées la consigne (c’est-à-dire la température souhaitée à l’intérieur du four) ainsi que la température réelle du four fourni par un capteur, et pour sortie, la commande du four ; cette sortie est ainsi reliée à l’entrée du système four.
L’ensemble forme ce qu’on appelle un « système asservi ».
Le régulateur peut alors être réalisé sous forme analogique (circuit électronique) ou numérique (microcontrôleur). Il existe également des régulateurs dans le commerce qui permettent ces fonctions, où l’automaticien peut choisir la méthode de régulation, ou par exemple entrer les coefficients dans le cadre d’un régulateur Proportionnel-Intégral-Dérivé.
Les systèmes
Un système est une modélisation d’un procédé en fonctionnement. Il possède une ou plusieurs entrées, et une ou plusieurs sorties. Les entrées du système sont appelées variables exogènes; elles rassemblent les perturbations et les variables manipulées, commandes ou grandeurs de réglage. Elles sont souvent représentées de manière générique par la lettre u ou e. Elles sont reliées au procédé en tant que tel par un actionneur.
Les sorties du système sont appelées variables contrôlées, mesures ou grandeurs réglées. Elles sont souvent représentées de manière générique par la lettre y. Le procédé est relié à la sortie du système par un capteur.
Dans le cas d’un système échantillonné, les entrées et sorties sont à temps discret, mais le système en lui-même demeure à temps continu. Le système inclut donc un convertisseur numérique-analogique en entrée, un convertisseur analogique-numérique en sortie et une horloge permettant de fixer la fréquence d'échantillonnage.
Il existe une infinité d’exemples de systèmes : des systèmes mécaniques, des systèmes électriques ou des procédés chimiques. La représentation du système ne pourra alors se faire qu’avec de bonnes connaissances dans le domaine physique correspondant.
Différents systèmes
Les systèmes peuvent être classés en plusieurs catégories.
Systèmes à temps continu, à temps discret
Systèmes à temps continus : ce sont les systèmes qui existent naturellement. Pour ces systèmes, le temps décrit la droite réelle.
Systèmes à temps discret : ce sont des systèmes pour lequel le temps est une variable discrète (on se ramène généralement au cas où décrit l’ensemble des nombres entiers). Sauf exception, ces systèmes n’existent pas à l’état naturel (la majorité des systèmes physiques naturels sont à temps continu), mais étant donné que la plupart des contrôleurs utilisés en automatique sont calculés par des processeurs numériques, il est parfois intéressant de modéliser le système commandé comme un système à temps discret.
Systèmes à événements discrets : systèmes dont le fonctionnement peut être modélisé par des événements discrets. Généralement, ces systèmes sont modélisés par des réseaux de Petri, des GRAFCET (qui en sont des cas particuliers très répandus, notamment dans l'industrie) ou par les algèbres de dioïdes. Des exemples sont les réseaux ferroviaires, ou le fonctionnement d’une chaîne de montage.
Systèmes hybrides : systèmes dont la modélisation nécessite l’utilisation des techniques liées aux systèmes continus et aux systèmes à évènements discrets, par exemple : une boîte de vitesses de voiture.
Systèmes monovariables, systèmes multivariables
Quatre possibilités existent:
le système a une entrée et une sortie, c’est un système monovariable ou SISO (Single Input Single Output),
le système a plusieurs entrées et plusieurs sorties, c’est un système multivariable ou MIMO (Multiple Input Multiple Output),
le système a une entrée et plusieurs sorties, système SIMO,
le système a plusieurs entrées et une sortie, système MISO.
Néanmoins, ces deux derniers termes sont peu utilisés.
Système invariant (ou stationnaire)
Ce sont des systèmes dont les paramètres du modèle mathématique ne varient pas au cours du temps.
Systèmes linéaires ou non linéaires
On dit qu’un système est linéaire s'il est régi par un système d'équations différentielles linéaires.
Aucun système n’est strictement linéaire, ne serait-ce que par les saturations (butées physiques, par exemple) qu’il comporte ou encore par les phénomènes d’hystérésis. Toutefois, un système non linéaire peut être considéré comme linéaire dans une certaine plage d’utilisation. Il faut toujours garder à l’esprit que le système sur lequel on peut travailler n’est qu’un modèle mathématique de la réalité, et que par conséquent il y a une perte d’information lors du passage au modèle. Bien sûr, il incombe à l’ingénieur de juger la pertinence de son modèle vis-à-vis des objectifs fixés.
Un système peut admettre une représentation linéaire et une autre représentation non linéaire. Par exemple, un système pourra être linéaire en utilisant des coordonnées cartésiennes, et deviendra non linéaire en coordonnées polaires.
Représentation des systèmes linéaires invariants
Les automaticiens ont l’habitude de représenter graphiquement un système asservi par l’utilisation de schémas fonctionnels.
Équation différentielle et fonction de transfert
Un système physique se décrit généralement avec des équations différentielles (par exemple le principe fondamental de la dynamique, caractéristique d’un condensateur ou d’une bobine…). La transformation de Laplace permet alors de passer de l’équation différentielle à une fonction de transfert, l'inverse n'étant exact que sous certaines hypothèses, car l'obtention d'une fonction de transfert suppose qu'on travaille à conditions initiales nulles.
Pour un système à temps discret on utilise la transformation en Z.
Ces transformations permettent d’étudier le comportement entrée-sortie du système, mais risquent de faire apparaître des modes cachés, du fait de l’impasse faite sur les conditions initiales.
Représentation temporelle
On peut s’intéresser au comportement du système lorsqu’on le soumet à certains signaux comme une impulsion de Dirac ou un échelon. On peut en déduire un certain nombre de caractéristiques du système.
Représentation fréquentielle
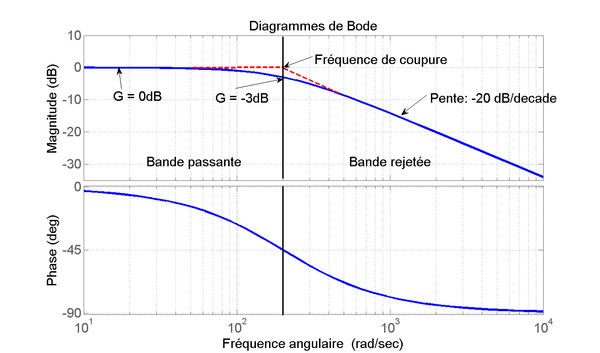
Diagramme de Bode d’un filtre passe-bas passif d’ordre 1. En pointillés rouges, l’approximation linéaire.
Le diagramme de Bode représente, sur des graphes séparés, le gain et la phase en fonction de la fréquence.
Le diagramme de Nyquist représente la partie imaginaire de la fonction de transfert en fonction de la partie réelle.
Le diagramme de Black représente le gain en fonction de la phase.
Représentation d’état
La représentation d’état est une représentation du système faisant appel au formalisme matriciel. On s’intéresse à des variables internes aux systèmes, appelées variables d’état. On représente alors la dérivée des variables d’état en fonction d’elles-mêmes et de l’entrée, et la sortie en fonction des variables d'état et de l'entrée (ainsi qu’éventuellement de certaines dérivées de l'entrée). La représentation d’état peut se déduire de la fonction de transfert.
De cette représentation on peut déduire le comportement entrée-sortie du système mais aussi un certain nombre d’autres informations comme la commandabilité ou l’observabilité. Ces notions ne sont toutefois pas propres à la représentation d’état, car elles sont des caractéristiques intrinsèques d'un système.
La représentation d’état peut aussi représenter un système non linéaire ou instationnaire.
Stabilité
Dans le cas des systèmes linéaires représentés par une fonction de transfert rationnelle, l’analyse des pôles permet de conclure sur la stabilité entrée-sortie (stabilité EBSB) du système. On rappelle que les pôles d’une fraction rationnelle sont les nombres complexes , ... qui annulent le dénominateur. Supposons que cette fonction de transfert soit propre.
Un système à temps continu (dont la fonction de transfert s'exprime dans le formalisme de la transformation de Laplace) est stable EBSB si, et seulement si tous ses pôles sont à partie réelle strictement négative.
Un système à temps discret (dont la fonction de transfert s'exprime dans le formalisme de la transformée en Z) est stable EBSB si, et seulement si tous ses pôles ont un module strictement inférieur à 1.
Les pôles de la fonction de transfert, dont il est question ci-dessus, sont appelés « pôles de transmission ». Si l’on prend pour le système une représentation plus complète que sa fonction de transfert, on peut définir les pôles du système. Par exemple, les pôles d'un système d’état linéaire invariant sont les valeurs propres de la matrice d’état. Le système est asymptotiquement (ou exponentiellement) stable, si, et seulement si ses pôles appartiennent au demi-plan gauche dans le cas du temps continu, et à l’intérieur du cercle unité dans le cas du temps discret. Ceci reste valable si on considère une représentation intrinsèque du système (modules de présentation finie sur l’anneau des opérateurs différentiels à coefficients constants) et s’étend, dans une large mesure (en faisant appel à des techniques mathématiques plus complexes, comme la théorie des modules sur un anneau non commutatif), au cas des systèmes linéaires à coefficients variant en fonction du temps.
En automatique, surtout dès qu’on aborde le cas des systèmes non linéaires, le terme « stabilité » doit être défini précisément car il existe une dizaine de sortes de stabilités différentes. On fait le plus souvent référence à la stabilité asymptotique ou la stabilité exponentielle (en), ces deux termes étant synonymes dans le cas des systèmes linéaires invariants. La stabilité au sens de Lyapunov est un concept également très important.
Dans le cas des systèmes non linéaires, la stabilité est généralement étudiée à l'aide de la théorie de Lyapunov.
Commande en boucle ouverte
La commande peut être calculée en boucle ouverte par un ordinateur ou un automate programmable industriel, en ne tenant pas compte des informations recueillies en temps réel. Cela revient par exemple à conduire une voiture les yeux fermés. Néanmoins, c’est ce type de commande que l’on conçoit lorsqu’on fait de la planification de trajectoire. On ne parle pas de « système asservi » dans un tel cas.
Asservissement
Système bouclé
La technique d’automatisation la plus répandue est le contrôle en boucle fermée. Un système est dit en boucle fermée lorsque la sortie du procédé est prise en compte pour calculer l'entrée. Généralement le contrôleur effectue une action en fonction de l’erreur entre la mesure et la consigne désirée. Le schéma classique d'un système linéaire pourvu d'un régulateur linéaire en boucle fermée est le suivant :

La boucle ouverte du système est composée de deux sous-systèmes : le procédé et le régulateur (ou « correcteur »). La fonction de transfert de ce système en boucle ouverte est donc :

Avec cette architecture on peut recalculer une nouvelle fonction de transfert du système, soit la fonction de transfert en boucle fermée, à l’aide des relations entre les différentes variables :

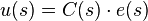
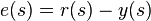
On obtient alors : 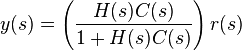
La fonction 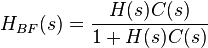 représente la fonction de transfert en boucle fermée. On peut remarquer que pour les systèmes à retour unitaire
représente la fonction de transfert en boucle fermée. On peut remarquer que pour les systèmes à retour unitaire : c’est la formule de Black qui permet de passer d’une fonction de transfert en boucle ouverte (à retour unitaire) à une fonction de transfert en boucle fermée.
: c’est la formule de Black qui permet de passer d’une fonction de transfert en boucle ouverte (à retour unitaire) à une fonction de transfert en boucle fermée.
Remarques :
La boucle de retour est le chemin qui part de la sortie et qui revient au comparateur avec le signe "moins". Dans cette boucle, il y a généralement un bloc représentant, dans la plus grande majorité des cas, un capteur. Si ce bloc a comme fonction de transfert "1" (ce qui équivaut à une absence de bloc car la multiplication par 1 ne change rien), on dit que le schéma-bloc est à retour unitaire. La formule précédemment énoncée n'est valable que si le schéma-bloc est à retour unitaire.
Quel que soit le schéma-bloc (unitaire ou non, avec ou sans perturbation...), le dénominateur de la fonction de transfert en boucle fermée est toujours (sauf cas de simplifications pôles/zéros, sources de modes cachés) le numérateur de la fraction rationnelle : , désignant la fonction de transfert en boucle ouverte c'est-à-dire le produit de tous les blocs de la boucle, y compris ceux de la boucle de retour.
L'étude de cette fonction de transfert en boucle fermée 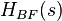 est un des éléments qui permettent l'analyse fréquentielle et temporelle du système bouclé. Il convient d'étudier également la fonction de sensibilité
est un des éléments qui permettent l'analyse fréquentielle et temporelle du système bouclé. Il convient d'étudier également la fonction de sensibilité 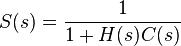 et (notamment pour les questions de stabilité) les deux autres fonctions de transfert
et (notamment pour les questions de stabilité) les deux autres fonctions de transfert 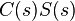 et
et 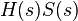 .
.
Le système bouclé est stable si aucune des quatre fonctions de transfert ci-dessus n'a de pôles dans le demi-plan droit fermé (c'est-à-dire axe imaginaire inclus). La stabilité du système bouclé peut s'étudier à partir de la fonction de transfert de la boucle ouverte , ainsi que des pôles de et de , grâce au Critère de Nyquist (en).
Exemple de boucle de régulation
Reprenons l’exemple du moteur automobile.
On le commande en choisissant l’ouverture du papillon des gaz intégré au système d’injection du moteur. L’ouverture est directement liée à la force appliquée sur le piston donc à l’accélération du véhicule. Disons qu’elles sont proportionnelles (on néglige les pertes et la résistance de l’air sur le véhicule).
On veut maintenir une certaine vitesse, 90 km/h par exemple. Dans ce cas, 90 km/h est la consigne, il faut la comparer à la vitesse réelle donnée par un tachymètre. La différence donne la variation de vitesse à réaliser. On en déduit l’accélération à demander au véhicule. Connaissant le rapport entre l’accélération et l’ouverture du papillon, on calcule l’ouverture à donner au papillon pour s’approcher de la vitesse de consigne. Le compteur de vitesse prend alors la nouvelle valeur de la vitesse pour réitérer l’opération. De cette manière, lorsqu’on approche de la vitesse voulue, l’accélération diminue jusqu’à s’annuler sans brutalité.
On obtient donc ce schéma.
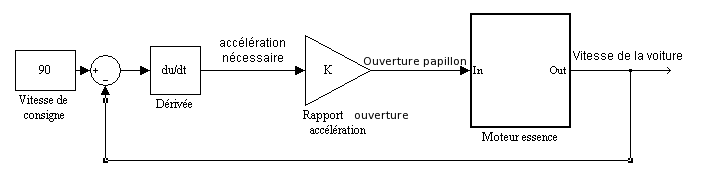
En réalité, à cause des pertes, il faut maintenir une certaine accélération entre autres pour lutter contre la résistance de l’air.
Les différentes techniques
Il existe différentes techniques pour synthétiser les régulateurs. La technique industrielle la plus largement utilisée est le régulateur PID qui calcule une action Proportionnelle, Intégrale et Dérivée en fonction de l’erreur consigne/mesure. Cette technique permet de satisfaire la régulation de plus de 90 % des procédés industriels. La commande à modèle interne (en), généralisation des régulateurs PI ou PID avec prédicteur de Smith (en), offre beaucoup plus de possibilités et est également répandue.
Des techniques avancées se basent sur la commande par retour d'état (ou commande par retour d'état reconstruit par un observateur). On peut aussi utiliser le formalisme du régulateur RST. Ces types de commande peuvent être conçus par placement de pôles ou (pour ce qui concerne les systèmes d’état) par minimisation d’un critère quadratique: commande LQ ou LQG.
Autres commandes :
La commande prédictive se basant sur l'utilisation d'un modèle dynamique du système pour anticiper son comportement futur.
La commande robuste permettant de garantir la stabilité par rapport aux perturbations et aux erreurs de modèle. Une commande robuste peut être conçue par minimisation d'un critère (par exemple de nature H-infini) ou par placement de pôles à condition que le choix des pôles du système bouclé soit judicieux. Encore faut-il souligner que pour un système multivariable, le choix des pôles du système bouclé ne détermine pas le régulateur de façon unique, et que pour un même choix de ces pôles, on peut obtenir des propriétés de robustesse fort différentes. Toute commande doit être suffisamment robuste.
La commande adaptative (en) qui effectue une identification en temps réel pour actualiser le modèle du système.
La logique floue utilisant un réseau de neurones ou un système expert.
Les contrôleurs non linéaires utilisant la théorie de Lyapunov, les commandes linéarisantes par bouclage et difféomorphisme (en prêtant une attention toute particulière à la méthode de linéarisation de manière à obtenir une bonne robustesse) ou la commande par modes glissants (en).
La commande par platitude différentielle (en). (en boucle ouverte), qui permet l'inversion de modèle sans passer par l'intégration des équations différentielles, et ainsi de calculer les signaux nécessaires sur les entrées pour garantir les trajectoires voulues en sortie.
Les commandes non-linéaires utilisant les concepts d'hyperstabilité, de passivité ou de dissipativité (dont on peut trouver un bref historique à l'article Stabilité de Lyapunov). Ces commandes ont connu un essor important depuis le milieu des années 1980, dans divers domaines tels que les systèmes mécaniques (robotique), électro-mécaniques, etc.

 词典释义:
词典释义:

 的;
的; 
 的, 无意识的, 不由
的, 无意识的, 不由 主的;
主的;  然而然产生的
然而然产生的
 装置
装置
 关闭
关闭
 扣除
扣除
 售票机
售票机
 离合器
离合器
 取款机
取款机 助洗衣店
助洗衣店
 驾驶
驾驶
 划帐
划帐
 开启的
开启的
 +mat心智+ique形容词后缀
+mat心智+ique形容词后缀
 词变化:
词变化:
 的;
的;
 ;
;
 化;
化;
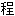 ;
;
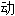 性;
性;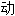 ;
;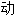 的;
的;
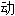 的, 无意识的, 不由
的, 无意识的, 不由
 主的
主的

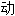 的automatiquef
的automatiquef
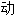 控制[工
控制[工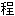 ]学,
]学, 
 装置
装置
 进刀
进刀
 筛分机
筛分机
 车钩
车钩
 进料;
进料; 
 进刀
进刀
 生产线
生产线
 变
变

 上料
上料
 交换机(电话)
交换机(电话)
 加工循环
加工循环 拍机
拍机

 剥壳
剥壳
 幻灯机
幻灯机
 调节装置
调节装置
 连接器
连接器
 闭锁装置
闭锁装置
 拉钩
拉钩
 离合器
离合器
 刹车
刹车
 油漆机
油漆机
 焊机
焊机
 造型机
造型机
 化机床
化机床
 化机床
化机床
 停车机构
停车机构
 上下料装置
上下料装置 行排尿
行排尿
 导航系统
导航系统
 导航
导航
 导航
导航
 装货盘机
装货盘机
 换档
换档
 灯塔
灯塔
 舵,
舵, 
 驾驶仪
驾驶仪

 跟随器
跟随器
 防护
防护 引导
引导
 进料调节器
进料调节器 调节器
调节器
 叫醒
叫醒 闭轴承
闭轴承
 调心轴承
调心轴承
 开伞拉带
开伞拉带
 的
的
 信号装置
信号装置
 焊
焊
 埋弧焊
埋弧焊
 分光计
分光计
 坐标制
坐标制
 制
制
 测距[仪、计、器]
测距[仪、计、器]
 装货车
装货车
 寄存处
寄存处


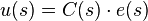
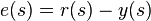
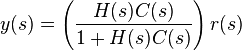
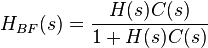 représente la fonction de transfert en boucle fermée. On peut remarquer que pour les systèmes à retour unitaire
représente la fonction de transfert en boucle fermée. On peut remarquer que pour les systèmes à retour unitaire
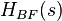 est un des éléments qui permettent l'analyse fréquentielle et temporelle du système bouclé. Il convient d'étudier également la fonction de sensibilité
est un des éléments qui permettent l'analyse fréquentielle et temporelle du système bouclé. Il convient d'étudier également la fonction de sensibilité 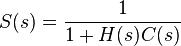 et (notamment pour les questions de stabilité) les deux autres fonctions de transfert
et (notamment pour les questions de stabilité) les deux autres fonctions de transfert 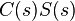 et
et 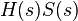 .
.