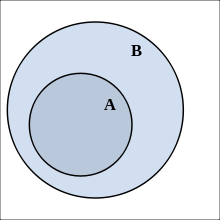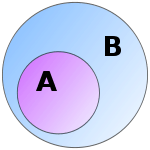
L'ensemble A est inclus dans l'ensemble B. On dit que A est sous-ensemble de B, ou que B est sur-ensemble de A.
En mathématiques, l’inclusion est une relation d'ordre entre ensembles. On dit qu'un ensemble A est inclus dans un ensemble B si tous les éléments de A sont aussi éléments de B. On dit dans ce cas que A est un sous-ensemble ou une partie de B, ou encore que B est sur-ensemble de A.
Cette relation n'est pas symétrique a priori, car il peut y avoir des éléments du deuxième ensemble qui n'appartiennent pas au premier. Plus précisément, il y a inclusion dans les deux sens entre deux ensembles si et seulement si ces deux ensembles sont égaux.
L'inclusion se note majoritairement avec le symbole « ⊂ » introduit par Schröder, même si beaucoup d'auteurs réservent ce symbole à l'inclusion stricte (c'est-à-dire excluant le cas d'égalité), suivant ainsi la norme ISO. L'inclusion au sens large peut alors être notée avec le symbole « ⊆ » de Felix Hausdorff, par analogie avec les symboles de comparaison numériques. Pour lever l'ambiguïté, l'inclusion stricte peut aussi être notée « ⊊ », à ne pas confondre avec la négation de l'inclusion, qui se note « ⊄ » ou « ⊈ ». Tous ces symboles peuvent être renversés de droite à gauche pour représenter les relations réciproques.
Définitions
Soient deux ensembles A et B. Par définition, A est inclus (au sens large) dans B si tout élément de A est un élément de B. A est inclus (au sens strict) dans B si de plus A ≠ B.
Notations symboliques
⊆
En notation symbolique, l’inclusion au sens large est notée ⊆ ; donc par définition (« ⇒ » désigne l'implication logique) :
-
A ⊆ B signifie ∀ x (x ∈ A ⇒ x ∈ B).
On peut aussi définir l'inclusion au sens large à partir de l'intersection ou de la réunion :
A ⊆ B si et seulement si A ∩ B = A ;
A ⊆ B si et seulement si A ∪ B = B.
⊂
⊂ est le symbole de l'inclusion stricte selon la norme ISO 31-11 (en) de l'organisation internationale de normalisation (qui mentionne toutefois l'autre usage). L'usage du symbole ⊂ pour l'inclusion stricte s'explique par l'analogie avec le symbole <.
⊊
L’inclusion au sens strict est parfois notée ⊊ :
-
A ⊊ B signifie A ⊆ B et A≠B.
Variantes d'écriture : 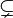
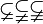 .
.
Inclusion, sous-ensembles et sur-ensembles, sous-ensembles propres
L'inclusion peut se dire de plusieurs façons, « A ⊆ B » peut aussi se lire :
« A est contenu dans B »,
« A est une partie de B »,
ou « A est un sous-ensemble de B ».
« B inclut A »,
« B contient A »,
« B est une extension de A »,
ou « B est un sur-ensemble de A ».
L'inclusion au sens strict, « A ⊊ B » peut aussi se lire :
« A est inclus dans B (au sens strict) »,
« A est strictement inclus dans B », etc.
« A est un sous-ensemble propre de B ».
Définition en compréhension
Une propriété des éléments d'un ensemble définit un sous-ensemble de celui-ci. Ainsi, en reprenant l'un des exemples ci-dessus, la propriété « être pair » définit, sur l'ensemble des entiers naturels N, l'ensemble 2N des entiers pairs. On dit que l'ensemble a été défini par compréhension et on note :
-
2N={n ∈ N | n est pair} = {n ∈ N | (∃q ∈ N) n=2q}
Toute propriété (quand on l'exprime dans un langage précis on parle de prédicat de ce langage) définit par compréhension un sous-ensemble d'un ensemble donné.
Ensemble des parties
L'ensemble de tous les sous-ensembles d'un ensemble E donné est appelé ensemble des parties de E, et noté habituellement « (E) », ou (écriture gothique) « (E) », voire simplement « P(E) » (lire dans tous les cas « P de E » ). On a ainsi :
-
X ∈
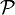 (E) si et seulement si X ⊆ E.
(E) si et seulement si X ⊆ E.
Par exemple si A = { a, b }, alors 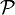 (A) = { Ø, { a }, { b }, A }.
(A) = { Ø, { a }, { b }, A }.
Dans ce cas on aura par exemple a ∈ A, donc {a} ⊆ A, c'est-à-dire {a} ∈ 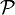 (A).
(A).
Les propriétés de l'ensemble des parties, en particulier celles ayant trait à la cardinalité, sont détaillées dans l'article ensemble des parties d'un ensemble. Pour le cas fini, qui relève de la combinatoire, voir aussi l'article combinaison.
Fonction caractéristique
Un sous-ensemble A d'un ensemble E peut être défini par sa fonction caractéristique , définie par χA(x) vaut 1 si x est élément de A, et 0 sinon :
-
![\forall x \in E[ \chi_A(x) = 1 \Leftrightarrow x \in A ]](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/94ec4baa03260c91ffc084d6dbe27b7a.png)
et donc (χA étant à valeurs dans {0,1})
-
![\forall x \in E[\chi_A( x) = 0 \Leftrightarrow x \not\in A ]](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/85e314907b883a8bc32d002aae4a78ba.png)
Réciproquement toute fonction χ de E dans {0,1} définit un sous-ensemble de E qui est {x ∈ E | χ(x) = 1}. On a donc une correspondance bijective entre les sous-ensembles de E et les fonctions de E dans {0,1}, c'est-à-dire entre (E) et {0,1}.
Exemples
Par exemple l'ensemble des entiers naturels non nuls ℕ est inclus dans l'ensemble des entiers naturels ℕ, de même que l'ensemble des entiers naturels pairs 2ℕ, mais 2ℕ n'est pas inclus dans ℕ car 0 ∈ 2ℕ, mais 0 ∉ ℕ :
-
ℕ ⊆ ℕ, 2ℕ ⊆ ℕ, 2ℕ ⊄ ℕ.
On peut remarquer que, comme il existe des entiers naturels non nuls qui ne sont pas pairs, 1 par exemple, ℕ n'est pas non plus inclus dans 2ℕ : ℕ ⊄ 2ℕ. On dit alors que ces deux ensembles ne sont pas comparables pour l'inclusion.
Propriétés de l'inclusion
L'ensemble vide est l'ensemble qui n'a pas d'éléments, et on le note Ø.
Proposition (ensemble vide). L'ensemble vide est sous-ensemble de tout ensemble, c'est-à-dire que pour tout ensemble A :
-
∅ ⊆ A
Démonstration : nous devons démontrer que Ø est un sous-ensemble de A, c'est-à-dire que tous les éléments de Ø sont des éléments de A, mais il n’existe pas d’éléments de Ø. Pour qui a un peu la pratique des mathématiques, l'inférence « Ø n’a pas d’éléments, donc tous les éléments de Ø sont des éléments de A » est évidente, mais cela peut être dérangeant pour le débutant. Il peut être utile de raisonner différemment (par l’absurde). Si nous avions supposé que Ø n' était pas un sous-ensemble de A, nous aurions pu trouver un élément de Ø n’appartenant pas à A. Comme il n’existe pas d’élément de Ø, c’est impossible et donc Ø est par conséquent un sous-ensemble de A.
Nous avons aussi la proposition suivante.
Proposition (réflexivité). Tout ensemble est inclus dans lui-même, c'est-à-dire que pour tout ensemble A :
-
A ⊆ A.
On dit que l'inclusion est une relation réflexive. Pour le prouver, il suffit de reprendre la définition de l’inclusion.
Une autre propriété qui elle aussi repose seulement sur la définition de l'inclusion est la transitivité.
Proposition (transitivité). Pour trois ensembles quelconques A, B et C, si A est un sous-ensemble de B et B est un sous-ensemble de C, alors A est un sous-ensemble de C, c'est-à-dire que :
-
(A ⊆ B et B ⊆ C) ⇒ A ⊆ C.
de même
-
(A ⊊ B et B ⊊ C) ⇒ A ⊊ C.
Contrairement aux propositions précédentes, qui se démontrent de façon purement logique, en revenant aux définitions, la propriété d'antisymétrie repose sur la notion même d'ensemble : c'est en fait la simple traduction d'une propriété fondamentale des ensembles, dite propriété d'extensionnalité, à savoir que deux ensembles sont égaux si et seulement s'ils ont les mêmes éléments.
Proposition (antisymétrie). Deux ensembles A et B sont égaux si et seulement si A est un sous-ensemble de B et B est un sous-ensemble de A, c'est-à-dire :
-
A = B si et seulement si (A ⊆ B et B ⊆ A)
Quel que soit l’ensemble E, l’inclusion munit donc son ensemble des parties (E) d’une relation d'ordre, qui n'est plus un ordre total dès que E possède au moins deux éléments. En effet si a et b sont deux éléments distincts de E, les singletons {a} et {b} sont des parties de E qui ne se comparent pas pour l'inclusion. Cet ordre a toujours un plus petit élément, Ø l'ensemble vide, et un plus grand élément, l'ensemble E.
Cet ordre n'est donc pas total en général mais a d'autres propriétés remarquables.
Proposition (intersection finie). Pour deux ensembles A et B quelconques, on peut définir l'intersection de A et B, qui est l'ensemble des éléments communs à A et à B, noté A ∩ B. Cet ensemble est le seul à être inclus dans A et dans B, et à contenir tout ensemble contenu à la fois dans A et dans B :
-
A ∩ B ⊆ A et A ∩ B ⊆ B ;
-
si C ⊆ A et C ⊆ B, alors C ⊆ A ∩ B.
On dit que l'ensemble A ∩ B est la borne inférieure de A et B pour l'inclusion.
On a une propriété analogue (on dit duale, en un sens précis) pour la réunion.
Proposition (réunion finie). Pour deux ensembles A et B quelconques, on peut définir la réunion de A et B, qui est l'ensemble des éléments appartenant à A ou à B, noté A ∪ B. Cet ensemble est le seul à contenir à la fois A et B, et à être contenu dans tout ensemble contenant à la fois A et B :
-
A ⊆ A ∪ B et B ⊆ A ∪ B ;
-
si A ⊆ C et B ⊆ C, alors A ∪ B ⊆ C.
On dit que A ∪ B est la borne supérieure de A et B pour l'inclusion.
Pour tout ensemble E l'inclusion munit donc (E) d'une structure d'ordre que l'on appelle un treillis. Du fait des propriétés de distributivité de la réunion vis-à-vis de l'intersection, et de l'intersection vis-à-vis de la réunion, ce treillis est dit distributif.
Des propriétés des intersections et réunions binaires, on pourrait déduire facilement un résultat analogue pour les intersections et réunions finies, mais on a un résultat plus fort :
Proposition (intersection et réunion quelconques). Pour une famille quelconque d'ensembles (Ai)i ∈ I, on peut définir l'intersection des éléments de la famille, ∩i ∈ IAi, et leur réunion ∪i ∈ IAi. L'intersection des Ai est le plus grand des ensembles inclus dans chacun des Ai, la réunion des Ai est le plus petit des ensembles incluant tous les Ai.
Le treillis de l'inclusion sur (E) est dit complet. Il s'agit même d'une algèbre de Boole, puisque tout sous-ensemble de E a un complémentaire dans E.
Proposition (complémentaire). Soit E un ensemble. On appellera complémentaire d'un sous-ensemble A de E, le sous-ensemble de E constitué des éléments de E qui ne sont pas dans A, et on le notera . On a :
-
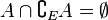 et
et
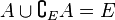
On montre alors que :
-
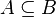 si et seulement si
si et seulement si
 .
.
Théorie axiomatique des ensembles
En théorie des ensembles, dans la théorie des ensembles de Zermelo ou de Zermelo-Fraenkel, l'inclusion n'est pas une notion primitive. elle est définie à partir de l'appartenance comme indiquée au début de l'article. Comme déjà mentionné, des propriétés de l'inclusion, comme la réflexivité et la transitivité, sont des conséquences purement logique de cette définition et l'antisymétrie de l'inclusion est exactement l'axiome d'extensionnalité.
L'existence d'un plus petit élément (ensemble vide) se montre par compréhension (voir axiome de l'ensemble vide). Il n'y a pas de plus grand élément pour l'inclusion dans l'univers de la théorie des ensembles : s'il existait un ensemble contenant tous les ensembles (au sens de l'inclusion) on pourrait, en utilisant le schéma d'axiomes de compréhension, dériver le paradoxe de Russell.
L'existence d'une borne inférieure (intersection) se démontre par compréhension. L'existence d'une borne supérieure (réunion) dans le cas d'un ensemble d'ensembles, nécessite un axiome spécifique, l'axiome de la réunion. À chaque fois l'axiome d'extensionnalité est utile pour démontrer l'unicité.
L’existence de l'ensemble des parties d'un ensemble nécessite également un axiome spécifique, l’axiome de l'ensemble des parties, et son unicité est encore une fois assurée par l’axiome d'extensionnalité.
L'appartenance et l'inclusion sont en général bien distinctes dans les mathématiques ordinaires. En théorie des ensembles une notion très utile est celle d'ensemble transitif : un ensemble dont tous les éléments sont aussi des sous-ensembles ! En particulier Les ordinaux sont des ensembles transitifs. La restriction de l'inclusion à un ordinal définit un bon ordre (et donc un ordre total), l'ordre strict correspondant est l'appartenance.
Si on introduit la notion de classe (que la notion de classe soit ou non formalisée dans la théorie, voir l'article correspondant), comme celle-ci correspond à la notion de prédicat, on peut définir de façon tout à fait analogue l'inclusion entre classes. La classe de tous les ensembles est maximale pour l'inclusion. On peut définir l'intersection et la réunion de deux classes, et donc d'un nombre fini de classes par conjonction et disjonction, le passage au complémentaire, par négation. Le complémentaire d'un ensemble dans une classe propre, en particulier dans la classe de tous les ensembles, ne peut cependant être un ensemble (par réunion). Il n'est pas question par contre non plus d'ensemble, ou même de classe, des parties d'une classe propre, celles-ci pouvant être elles-mêmes des classes propres.

 词典释义:
词典释义:
 , 附入
, 附入 ; 插入
; 插入 ;
; 
 在内
在内
 文件
文件
 在价钱中
在价钱中
 该日在内
该日在内 , 不伸出
, 不伸出
 , 附上
, 附上 (放在n. 前无性数变化; 放在n. 后性数要与n. 一致)
(放在n. 前无性数变化; 放在n. 后性数要与n. 一致)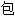
 在内
在内 ;
; , 被供应
, 被供应 ;
; ,整体
,整体 ,;
,; 平民;
平民; ;
;

 ,
,
 在内
在内 ,封入
,封入 ;【植物学】内藏
;【植物学】内藏 , 不伸出
, 不伸出

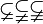 .
.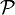 (E)
(E) ![\forall x \in E[ \chi_A(x) = 1 \Leftrightarrow x \in A ]](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/94ec4baa03260c91ffc084d6dbe27b7a.png)
![\forall x \in E[\chi_A( x) = 0 \Leftrightarrow x \not\in A ]](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/85e314907b883a8bc32d002aae4a78ba.png)
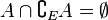
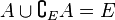
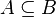
 .
.