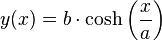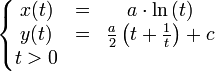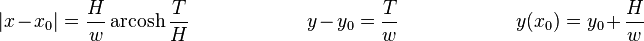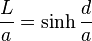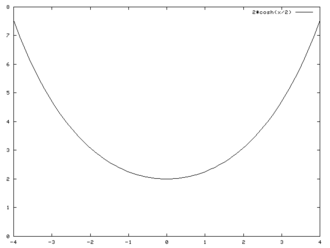
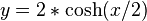
En mathématiques, la chaînette est une courbe plane transcendante, qui correspond à la forme que prend un câble (ou une chaîne) lorsqu'il est suspendu par ses extrémités et soumis à une force gravitationnelle uniforme (son propre poids). On lui donne parfois le nom de vélaire.
Cette définition suppose toutefois que le câble, la corde ou la chaîne n'exerce aucune force élastique de flexion (ni de friction aux surfaces transversales de contacts des mailles de la chaînette) et donc que la seule force en jeu est la force de gravitation exercée de façon uniforme sur toute la longueur. Cette définition suppose aussi que la longueur totale du câble, ou de n'importe quelle section de celui-ci, reste invariante lorsque s'exercent des forces de traction longitudinales (donc que le câble ne subit aucune élongation élastique à cause de cette traction, le cas idéal n'étant alors pas celui de la cordelette, mais celui d'une très fine chaînette à maillons indéformables, chacun d'eux étant très court en comparaison de la longueur totale de la chaînette).
Pour que la force de gravitation soit uniforme, on admet que toutes les sections de même longueur du câble ou de la corde sont de même poids, quelle que soit cette longueur de section (rapporté au cas de la chaînette idéale, les maillons élémentaires sont tous de forme et de taille identiques, mais aussi de masses identiques donc faits d’un matériau solide dont la masse volumique est homogène). D'autre part on doit aussi admettre que les forces de gravitation exercées sur chacune de ces sections sont égales (et ne dépendent donc pas de la position des sections, ce qui n’est possible que si la distance entre leur centre de gravité et le centre de gravité de la Terre est pratiquement identique entre deux sections quelconques, et donc que la longueur totale du câble est négligeable par rapport à la distance entre le milieu du câble et le centre de la Terre, de sorte que le module et la direction du champ de gravité terrestre sont alors pratiquement constants sur toute la longueur du câble ou de la chaînette idéale).
Enfin, on suppose que quelle que soit la forme de la chaînette, celle-ci reste confinée sur toute sa longueur dans le plan formé par la position de ses extrémités et la direction constante du champ gravitationnel : toutes les forces d'action ou de réaction s'exercent alors dans ce plan sans qu'intervienne aucune force de torsion supplémentaire (ou que les forces d’action exercées hors de ce plan sur toute section de la chaînette sont partout et constamment équilibrées par la réaction des forces de torsion égales en module et opposées en direction aux forces d’action, de sorte que les éventuelles forces de torsion, élastiques ou non, n'entrent pas en jeu dans la forme obtenue de la chaînette dans ce plan : ce cas s'applique aux fils, cordes et câbles, formés de torons soumis en interne à de telles forces de torsion maintenues en équilibre par des contre-torsions).
Étymologie et histoire
Caténaire, formée d'un câble porteur et d'un câble linéaire inférieur, reliés par des pendules : la chaînette virtuelle se situe entre les deux câbles.
Le problème de la forme prise par un fil pesant flexible a intéressé très tôt les mathématiciens. Galilée pensait que cette forme devait être un arc de parabole, mais la preuve du contraire fut apportée en 1627 par Joachim Jung dans sa Geometrica Empirica et en ** par Huygens.
En 1691, Leibniz, Jean Bernoulli et Huygens, sous l’impulsion d’un défi lancé par Jacques Bernoulli, démontrent quasi simultanément que la forme exacte est une chaînette. C’est d’ailleurs Huygens qui la baptise ainsi, dans une lettre adressée à Leibniz.
Délaissant le vocable latin du problema funicularium, (problème relatif à la corde), utilisé par les Bernoulli, Huygens utilise le mot catenaria, courbe relative à la chaîne (catena), puis passe au français chaînette, renouant ainsi avec le terme catenella utilisé par Galilée (alors que les mathématiciens anglophones conserveront la désignation de Huygens pour la nommer catenary, le même mot anglais étant traduit en français par caténaire avec la même origine latine, mot utilisé aussi en français pour certaines constructions autoportées en forme de chaînette).
Certains auteurs francophones lui donnent donc aussi le nom de caténaire bien que la caténaire désigne plutôt l’association d’un câble autoporté soutenant dans le même plan un second câble linéaire dans sa partie inférieure, les deux câbles étant soumis à une force de traction longitudinale équilibrée par une série de pendules reliant verticalement les deux câbles, le système de portage déformant la caténaire porteuse pour lui donner une forme plus proche en fait de la parabole, la chaînette n'étant présente virtuellement que dans l'axe central entre les deux câbles où sont articulés les pendules de longueur variable.
L'intérêt du montage porteur en caténaire est de permettre de donner une forme quasi rectiligne au câble inférieur. Cela permet par exemple d'améliorer le contact et d'équilibrer (et même réduire) globalement les forces de frottement dans les systèmes d'alimentation électrique ferroviaire (en évitant autant que possible les ruptures causées par des chocs répétés contre le câble d'alimentation), mais aussi de réduire la longueur totale du câble inférieur afin de limiter sa résistance électrique totale (donc de réduire les pertes d'énergie en ligne au sein de ce câble) pour les caténaires de transport d'énergie à longue distance, sans avoir à augmenter de façon très importante la tension des câbles (ce qui les fragilise progressivement au cours du temps par des élongations inélastiques).
En effet, la forme de chaînette est celle qui permet de minimiser sa tension longitudinale : en augmentant la flèche de courbure (l’écartement maximum du câble par rapport à la ligne droite joignant les points d'attachement), donc aussi la longueur totale du câble entre les deux points fixes d’attachement, on réduit sensiblement cette tension longitudinale et donc aussi les élongations inélastiques et les risques de rupture rapide du câble.
Cette propriété de la chaînette est utilisée dans les câbles porteurs d'un téléphérique (ou d'autres systèmes de portage similaires comme le télésiège) qui adoptent la forme d'une chaînette entre les points d'attachement aux pylônes fixes, ou entre le point de charge d’une nacelle et chacun des points d'attachement aux pylônes précédent et suivant ; la seule contrainte supplémentaire exercée sur le câble est alors la flexion exercée aux points d’intersection des arcs de chaînettes successifs (aux pylônes ou au-dessus d’une nacelle), une flexion dont on peut réduire l'effet inélastique indésirable en remplaçant ce point par un arc solide de soutien (par exemple le réa circulaire d’une poulie), d'une longueur suffisante pour distribuer et limiter la courbure de flexion exercée localement sur le câble. Ainsi il suffit d’un nombre très réduit de pylônes fixes pour porter le câble et franchir des distances très importantes entre deux pylônes, avec une seule chaînette entre eux, tout en conservant une tension de câble réduite qui en augmente la résistance et la charge utile de transport.
La chaînette des lignes à haute tension varie en fonction de la quantité d'énergie transportée et des conditions météorologiques. Le courant permanent admissible désigne le courant maximum pouvant être transporté à un moment donné sans que le câble ne se rapproche trop du sol (en raison de la dilatation thermique due à l'effet Joule).
Définition mathématique
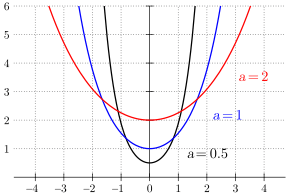
L’équation cartésienne de la forme de la chaînette est :
-
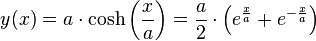 ,
,
dans laquelle désigne le cosinus hyperbolique.
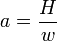 est le rapport de la composante horizontale
est le rapport de la composante horizontale 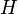 de la tension
de la tension 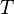 à la masse linéique
à la masse linéique 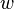 , masse par unité de longueur.
, masse par unité de longueur.
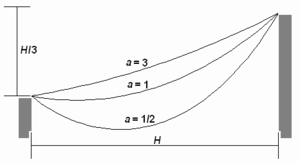
Cette équation dépend d’un seul paramètre 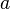 (une constante, qui a la dimension d’une longueur dans son interprétation physique). Une courbe d’équation :
(une constante, qui a la dimension d’une longueur dans son interprétation physique). Une courbe d’équation :
n’est généralement pas une chaînette au sens strict. Cependant, la forme de la courbe ne varie pas à une constante additive près (déterminant sa hauteur de portée), et la courbe suivante sera considérée aussi comme une chaînette généralisée :
On peut également la voir sous la forme d’une équation paramétrique :
Il peut être commode de prendre pour paramètre la tension qui croît avec l'altitude du point. Dans ces conditions, par rapport à des axes quelconques :
Si l'allongement de la ligne ne peut être négligé, la longueur au repos 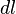 d'un petit élément devient sous tension, conformément à la loi de Hooke :
d'un petit élément devient sous tension, conformément à la loi de Hooke :
-
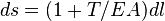 (
(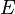 : module d'Young,
: module d'Young, 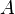 : section de la ligne)
: section de la ligne)
Les projections horizontale et verticale du petit élément étant modifiées dans les mêmes proportions, pour obtenir les équations paramétriques correspondantes, il faut différentier les deux équations précédentes, multiplier les résultats par le facteur d'accroissement et intégrer de nouveau. Chacune des deux équations contient alors un second membre corrigé par un terme inversement proportionnel à la rigidité 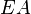 et la courbe résultante n'est plus une chaînette.
et la courbe résultante n'est plus une chaînette.
Calcul mécanique
La théorie de la chaînette décrit la courbe d'équilibre d'une ligne (chaîne ou câble) suspendue entre deux points, homogène, inextensible, sans rigidité en flexion, soumise à son seul poids. Cette dernière condition assure que toute la courbe est située dans un plan vertical, le système de coordonnées étant naturellement  horizontal,
horizontal, 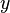 vertical.
vertical.
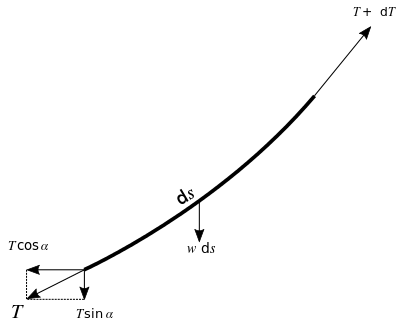
Pour établir les conditions d'équilibre on raisonne comme en résistance des matériaux en coupant par la pensée la ligne en un point arbitraire et en faisant apparaître les forces de liaison. En l'absence de rigidité en flexion il n'y a ni effort tranchant ni moment fléchissant mais un seul effort axial nommé tension, étant l'angle de celle-ci avec l'horizontale. Ainsi la composante horizontale s'écrit et la composante verticale .
L'absence de rigidité en flexion crée par contre des grandes déformations qui conduisent à étudier l'équilibre d'un petit élément de longueur 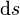 . Il subit une force horizontale nulle et une force verticale égale à son poids
. Il subit une force horizontale nulle et une force verticale égale à son poids 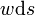 (où
(où 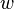 est le poids par unité de longueur), ce qui conduit aux équations différentielles
est le poids par unité de longueur), ce qui conduit aux équations différentielles
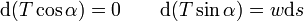
L'intégration de la première équation donne 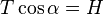 ,
,
la constante d'intégration 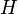 étant la composante horizontale de la force : la composante horizontale de la force est une constante en tout point de la courbe.
étant la composante horizontale de la force : la composante horizontale de la force est une constante en tout point de la courbe.
La seconde donne  .
.
Ici, la constante d'intégration, dont la valeur dépend de l'origine des abscisses curvilignes, correspond au point le plus bas de la courbe où la force verticale change de signe.
En élevant au carré et en sommant on obtient la loi de variation de la tension en fonction de l'abscisse curviligne :
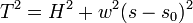
En divisant les deux équations de base on obtient la pente de la courbe :
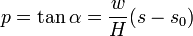
La dérivation par rapport à  conduit à
conduit à
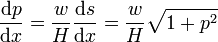
L'intégration donne 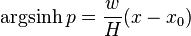 . En inversant il vient :
. En inversant il vient :
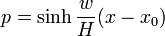
Une nouvelle intégration donne l'équation de la chaînette :
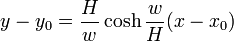
De la pente on déduit également l'abscisse curviligne :
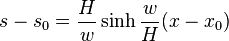
ainsi que la composante verticale de la tension :

D'où la tension elle-même :
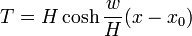
Aspects pratiques
La solution du problème est simple si l'on se donne les caractéristiques de la ligne (longueur et poids linéaire) et les deux composantes de la force appliquée à une extrémité pour calculer son extension (distances horizontale et verticale entre les supports). Les formules correspondantes définissent le module de base de tout calcul.
Si l'élasticité de la ligne ne peut plus être négligée, elle est prise en compte en appliquant la loi de Hooke, ce qui entraîne simplement une complication du calcul de l'extension dans le module de base.
Si les lignes sont constituées par une succession de segments de caractéristiques différentes, l'appel répété du module de base permet d'obtenir pour la ligne un résultat analogue à celui du segment en transmettant les forces d'un segment à un autre et en totalisant les extensions.
S'il existe un fond sur lequel repose une partie de la ligne, la force verticale appliquée à une extrémité permet de déterminer la longueur suspendue non déformée à ajouter à la longueur posée sur le fond.
Dans tous ces cas, il est donc possible d'obtenir pour la ligne un module qui transforme les caractéristiques de la ligne et la force à une extrémité en l'extension et la force à l'autre extrémité. Malheureusement, ces calculs relativement simples ne sont pas adaptés aux problèmes concrets dans lesquels on souhaite généralement calculer les forces aux deux extrémités en fonction des caractéristiques et de l'extension. Deux boucles de dichotomie, inconditionnellement convergentes, résolvent le problème.
Propriétés
L'axe des ordonnées est axe de symétrie de la courbe. Pour l'axe des abscisses, on parle de base.
La chaînette est un cas particulier d'alysoïde et de courbe de Ribaucour.
La chaînette est presque verticale près des points de suspension, car c'est là que le poids le plus important tire le plus la chaîne vers le bas. En revanche, vers le bas de la courbe, l'inclinaison diminue peu à peu puisque la chaîne supporte de moins en moins de poids. C'est d'ailleurs une des différences entre la chaînette et la parabole : pour une longueur égale, la parabole est plus « pointue » dans sa partie inférieure. Plus généralement aucune courbe dont l'ordonnée est proportionnelle à une puissance de l'abscisse ne monte aussi vite qu'une chaînette.
Applications
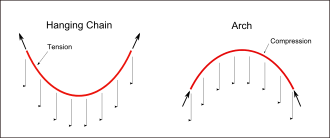
L'application de la courbe de la chaînette à la construction d'arches est attribuée au physicien anglais Robert Hooke, dans le contexte de la reconstruction de la Cathédrale Saint-Paul de Londres, où il a fait allusion à une caténaire (« catenary curve »), mais il n'en réalisa qu'une « approximation ».
Autour de 1671, Robert Hooke a annoncé à la Royal Society qu'il avait résolu le problème de la forme optimale d'un arc. En 1676, il a publié la solution dans une annexe à son livre « Une description des hélioscopes, et divers autres instruments ». Il a écrit en p. 31, qu'il avait trouvé « une véritable forme mathématique et mécanique de toutes sortes d'arches pour le bâtiment », la solution étant cryptée dans une anagramme. Il n'a pas fourni de son vivant, la traduction latine de celle-ci, qui n'a été donnée que par son exécuteur testamentaire, en 1705, deux ans après sa mort : « Ut continuum pendet flexile, sic stabit contiguum rigidum inversum », ce qui signifie approximativement « De même que pend un fil flexible, de même, en inversant, on trouve les pièces contiguës d'une arche ». Robert Hooke avait compris que les matériaux de construction ne peuvent supporter que des forces de compression et pas les efforts de traction, en contraste direct avec une simple corde suspendue qui peut résister à la traction mais qui peut se déformer par compression.
La chaînette n'apparaît pas seulement dans la forme d'une chaîne ou d'un câble suspendu comme : au gratte-ciel Marquette Plaza, à Minneapolis, Minnesota, construit en 1973, par l'architecte américano-letton, Gunnar Birkerts, qui a été le siège régional de la Réserve fédérale des États-Unis, de 1973 à 1997, au gratte-ciel Kingdom Centre, construit par Ellerbe Becket (en) et Omrania and Associates (en), à Riyad, Arabie saoudite, terminé en 2012.
au gratte-ciel Marquette Plaza, à Minneapolis, Minnesota, construit en 1973, par l'architecte américano-letton, Gunnar Birkerts, qui a été le siège régional de la Réserve fédérale des États-Unis, de 1973 à 1997,
au gratte-ciel Kingdom Centre, construit par Ellerbe Becket (en) et Omrania and Associates (en), à Riyad, Arabie saoudite, terminé en 2012.
La chaînette
Marquette Plaza à Minneapolis
Vue sur Riyad et la tour du Kingdom Centre
On la trouve aussi sous deux formes : la chaînette verticale, dans le profil d’une voile rectangulaire attachée à deux barres horizontales, enflée par un vent soufflant perpendiculairement à ces barres, en négligeant le poids propre de la voile par rapport à la force du vent. C'est cette propriété qui justifie le nom de « vélaire » (voile) donné par Jacques Bernoulli. la chaînette renversée, pour un arc dont la stabilité est assurée par son propre poids (structure autoportante). Relèvent de cette technique : La courbe tracée sur l'ostracon, (3 dynastie), trouvé à Saqqarah, en Égypte, en 1925, est très proche de la chaînette. Elle a été analysée par l'égyptologue anglais Battiscombe George Gunn en 1926, dans un article publié dans le volume 26 des Annales du Service des Antiquités de l'Égypte, Institut de France, archéologie orientale, La voûte nubienne, L’arc de Ctésiphon du palais de Taq-e Kisra, près de Bagdad en Irak, construit en 540, Le dôme de la cathédrale Santa Maria del Fiore à Florence, d'un poids de 37 000 tonnes, dôme en briques construit par l'architecte italien Filippo Brunelleschi de 1420 à 1436 (dôme le plus grand du monde avec 45 mètres de diamètre), La coupole intermédiaire du dôme du Panthéon de Paris, dôme d'un poids total de 17 000 tonnes, conçu par l'architecte Jacques-Germain Soufflot. Construction débutée en 1758, puis reprise par Soufflot en **, interrompue par sa mort en 1780, et terminée par ses successeurs Jean-Baptiste Rondelet et Maximilien Brébion, pour une inauguration en 1790, Les essais architecturaux d'Antoni Gaudí, connus aussi sous le nom d’« arcs caténaires » (« arcos catenarios »), et particulièrement à Barcelone, à la Casa Milà, construite entre 1906 et 1910, ou dès 1882, à la Sagrada Família. La Masia Freixa (es), à Terrassa, Espagne, ancienne fabrique construite en 1896, puis remaniée en résidence familiale, entre 1907 et 1914, par l'architecte moderniste catalan, Lluís Muncunill i Parellada (es). On y retrouve particulièrement l'influence d'Antoni Gaudí, dans l'utilisation des « arcs caténaires », Le hangar à dirigeables d'Écausseville, construit entre 1917 et 1919, par l'ingénieur Henry Lossier, appliquant le Système Hennebique, procédé de construction en béton armé de l'ingénieur François Hennebique, L'arche (Gateway Arch) du Jefferson National Expansion Memorial, construite par l'architecte finno-américain Eero Saarinen à Saint Louis, entre 1963 et 1965. On peut cependant parler de « chaînette aplatie » (« nosed catenary »), car l'architecte, n'étant pas satisfait de la courbure au sommet, a modifié les constantes de l'équation, pour atteindre cette forme au sommet, sur la suggestion de l'ingénieur structurel germano-américain, Hannskarl Bandel. Le Sheffield Winter Garden (en), est la plus grande serre urbaine d'Europe, construite à Sheffield, par le cabinet d'ingéniérie BuroHappold Engineering (en), et inaugurée par la reine Élisabeth II, le 22 mai 2003. L'Arche de Tchernobyl, est une nouvelle enceinte de confinement de la radioactivité, et doit recouvrir le premier sarcophage fissuré. Le projet a été décidé en 1992, par l'Ukraine, et signé le 17 septembre 2007, avec le consortium français Novarka, le pilote du projet. L'arche en cours de construction, pesait 30 000 tonnes à l'été 2015, et devrait être livrée fin 2017.
la chaînette verticale, dans le profil d’une voile rectangulaire attachée à deux barres horizontales, enflée par un vent soufflant perpendiculairement à ces barres, en négligeant le poids propre de la voile par rapport à la force du vent. C'est cette propriété qui justifie le nom de « vélaire » (voile) donné par Jacques Bernoulli.
la chaînette renversée, pour un arc dont la stabilité est assurée par son propre poids (structure autoportante). Relèvent de cette technique : La courbe tracée sur l'ostracon, (3 dynastie), trouvé à Saqqarah, en Égypte, en 1925, est très proche de la chaînette. Elle a été analysée par l'égyptologue anglais Battiscombe George Gunn en 1926, dans un article publié dans le volume 26 des Annales du Service des Antiquités de l'Égypte, Institut de France, archéologie orientale, La voûte nubienne, L’arc de Ctésiphon du palais de Taq-e Kisra, près de Bagdad en Irak, construit en 540, Le dôme de la cathédrale Santa Maria del Fiore à Florence, d'un poids de 37 000 tonnes, dôme en briques construit par l'architecte italien Filippo Brunelleschi de 1420 à 1436 (dôme le plus grand du monde avec 45 mètres de diamètre), La coupole intermédiaire du dôme du Panthéon de Paris, dôme d'un poids total de 17 000 tonnes, conçu par l'architecte Jacques-Germain Soufflot. Construction débutée en 1758, puis reprise par Soufflot en **, interrompue par sa mort en 1780, et terminée par ses successeurs Jean-Baptiste Rondelet et Maximilien Brébion, pour une inauguration en 1790, Les essais architecturaux d'Antoni Gaudí, connus aussi sous le nom d’« arcs caténaires » (« arcos catenarios »), et particulièrement à Barcelone, à la Casa Milà, construite entre 1906 et 1910, ou dès 1882, à la Sagrada Família. La Masia Freixa (es), à Terrassa, Espagne, ancienne fabrique construite en 1896, puis remaniée en résidence familiale, entre 1907 et 1914, par l'architecte moderniste catalan, Lluís Muncunill i Parellada (es). On y retrouve particulièrement l'influence d'Antoni Gaudí, dans l'utilisation des « arcs caténaires », Le hangar à dirigeables d'Écausseville, construit entre 1917 et 1919, par l'ingénieur Henry Lossier, appliquant le Système Hennebique, procédé de construction en béton armé de l'ingénieur François Hennebique, L'arche (Gateway Arch) du Jefferson National Expansion Memorial, construite par l'architecte finno-américain Eero Saarinen à Saint Louis, entre 1963 et 1965. On peut cependant parler de « chaînette aplatie » (« nosed catenary »), car l'architecte, n'étant pas satisfait de la courbure au sommet, a modifié les constantes de l'équation, pour atteindre cette forme au sommet, sur la suggestion de l'ingénieur structurel germano-américain, Hannskarl Bandel. Le Sheffield Winter Garden (en), est la plus grande serre urbaine d'Europe, construite à Sheffield, par le cabinet d'ingéniérie BuroHappold Engineering (en), et inaugurée par la reine Élisabeth II, le 22 mai 2003. L'Arche de Tchernobyl, est une nouvelle enceinte de confinement de la radioactivité, et doit recouvrir le premier sarcophage fissuré. Le projet a été décidé en 1992, par l'Ukraine, et signé le 17 septembre 2007, avec le consortium français Novarka, le pilote du projet. L'arche en cours de construction, pesait 30 000 tonnes à l'été 2015, et devrait être livrée fin 2017.
La courbe tracée sur l'ostracon, (3 dynastie), trouvé à Saqqarah, en Égypte, en 1925, est très proche de la chaînette. Elle a été analysée par l'égyptologue anglais Battiscombe George Gunn en 1926, dans un article publié dans le volume 26 des Annales du Service des Antiquités de l'Égypte, Institut de France, archéologie orientale,
La voûte nubienne,
L’arc de Ctésiphon du palais de Taq-e Kisra, près de Bagdad en Irak, construit en 540,
Le dôme de la cathédrale Santa Maria del Fiore à Florence, d'un poids de 37 000 tonnes, dôme en briques construit par l'architecte italien Filippo Brunelleschi de 1420 à 1436 (dôme le plus grand du monde avec 45 mètres de diamètre),
La coupole intermédiaire du dôme du Panthéon de Paris, dôme d'un poids total de 17 000 tonnes, conçu par l'architecte Jacques-Germain Soufflot. Construction débutée en 1758, puis reprise par Soufflot en **, interrompue par sa mort en 1780, et terminée par ses successeurs Jean-Baptiste Rondelet et Maximilien Brébion, pour une inauguration en 1790,
Les essais architecturaux d'Antoni Gaudí, connus aussi sous le nom d’« arcs caténaires » (« arcos catenarios »), et particulièrement à Barcelone, à la Casa Milà, construite entre 1906 et 1910, ou dès 1882, à la Sagrada Família.
La Masia Freixa (es), à Terrassa, Espagne, ancienne fabrique construite en 1896, puis remaniée en résidence familiale, entre 1907 et 1914, par l'architecte moderniste catalan, Lluís Muncunill i Parellada (es). On y retrouve particulièrement l'influence d'Antoni Gaudí, dans l'utilisation des « arcs caténaires »,
Le hangar à dirigeables d'Écausseville, construit entre 1917 et 1919, par l'ingénieur Henry Lossier, appliquant le Système Hennebique, procédé de construction en béton armé de l'ingénieur François Hennebique,
L'arche (Gateway Arch) du Jefferson National Expansion Memorial, construite par l'architecte finno-américain Eero Saarinen à Saint Louis, entre 1963 et 1965. On peut cependant parler de « chaînette aplatie » (« nosed catenary »), car l'architecte, n'étant pas satisfait de la courbure au sommet, a modifié les constantes de l'équation, pour atteindre cette forme au sommet, sur la suggestion de l'ingénieur structurel germano-américain, Hannskarl Bandel.
Le Sheffield Winter Garden (en), est la plus grande serre urbaine d'Europe, construite à Sheffield, par le cabinet d'ingéniérie BuroHappold Engineering (en), et inaugurée par la reine Élisabeth II, le 22 mai 2003.
L'Arche de Tchernobyl, est une nouvelle enceinte de confinement de la radioactivité, et doit recouvrir le premier sarcophage fissuré. Le projet a été décidé en 1992, par l'Ukraine, et signé le 17 septembre 2007, avec le consortium français Novarka, le pilote du projet. L'arche en cours de construction, pesait 30 000 tonnes à l'été 2015, et devrait être livrée fin 2017.
La chaînette renversée
Voûte nubienne, en Égypte
L’arc de Ctésiphon du palais de Taq-e Kisra à Bagdad, Irak
Le dôme de la Cathédrale Santa Maria del Fiore à Florence
Le dôme du Panthéon de Paris
arcs caténaires de la Casa Milà à Barcelone
arcs caténaires de la Masia Freixa, à Terrassa, Espagne
Le hangar à dirigeables d'Écausseville
La Gateway Arch à Saint-Louis
Le Sheffield Winter Garden à Sheffield
Arche de confinement, en construction à Tchernobyl


Le dôme de la basilique Saint-Pierre de Rome, (basilique construite entre 1506 et 1626), conçu par Michel-Ange, ne relève pas de ce modèle de construction. Le physicien Giovanni Poleni sera mandaté par le pape Benoît XIV en 1743, pour la vérification statique de l'équilibre, à la suite de l'apparition de fissures dans la coupole dès 1741. Il constatera que Michel-Ange, puis son successeur Giacomo della Porta, se sont éloignés de cette courbe idéale. S'appuyant aussi sur les travaux du mathématicien écossais James Stirling (1717), et de la validation scientifique de la courbe de la chaînette, Giovanni Poleni proposera au pape, à l'été 1743, de renforcer la coupole par sécurité, par cinq anneaux métalliques, qui seront posés de 1743 à 1748, (plus un sixième anneau, posé en remplacement d'un des trois anneaux d'origine, inclus dans la maçonnerie, qui est apparu cassé). Ces six anneaux la ceinturent encore aujourd’hui.
La coupole intermédiaire du dôme de la Cathédrale Saint-Paul de Londres, et contrairement à une croyance populaire très répandue, ne relève pas de ce modèle de construction. Ce dôme d'un poids total de 65 000 tonnes, a été construit par l'architecte Christopher Wren avec la collaboration de Robert Hooke. L'étude a débuté en 1669, pour une inauguration en 1708. Bien que les deux architectes aient eu connaissance des propriétés remarquables de la « courbe caténaire » (« catenary curve »), ils étaient incapables à l'époque, d'en trouver une formulation mathématique exacte (qui n'est venue qu'en 1691 avec Bernoulli, Leibniz et Huygens). On retrouve dans l'esquisse pour la construction du dôme, datant de 1690, une « approximation » de la courbe de la chaînette renversée : cette courbe est une parabole cubique (voir la figure 2 du document en référence, et les trois courbes superposées). Le dôme est formé par le conoïde créé par la rotation de la demi-parabole cubique y = x, sur l'axe des ordonnées.
Diverses courbes et formes
La courbe de la corde à sauter
Une corde soumise à une force peut prendre d'autres formes : C'est le cas de la « courbe de la corde à sauter », qui subit non seulement une force distribuée équitablement à son propre poids (qui lui donne la forme d'une chaînette quand elle n'est pas en rotation), mais aussi une force centrifuge plus importante au centre de la corde à sauter (en rotation) qu'à ses extrémités, ce qui déforme la chaînette au point de lui faire prendre une forme plus pointue, voire à la limite triangulaire avec une vitesse de rotation tendant vers l’infini, car les forces liées au poids de la corde sont négligeables, par rapport à la force centrifuge. Plus la corde tourne vite, plus elle se déforme et le différentiel de tension entre la partie supérieure et la partie inférieure de la corde augmente, ce différentiel étant maximum au milieu de la longueur de corde (qui sera donc le point de rupture de celle-ci si on la tourne trop vite).
La contrainte la plus forte exercée sur une structure en chaînette est celle d'un poids maximum porté en son centre : c’est le cas de la corde à sauter en rotation, où la force centrifuge liée à sa rotation est maximale au centre de la corde (là où l’écartement par rapport à l’axe de rotation est maximum), ou si la corde supporte un poids suspendu en son centre (comme sur une corde à linge si on ne fixe pas les vêtements portés sur le fil pour éviter qu'ils glissent tous vers le milieu de la corde).
La caténoïde

Lorsqu’on écarte deux cercles initialement jointifs juste sortis d’une solution savonneuse, la surface tubulaire qui se crée entre ces deux profils a un profil de chaînette : il s’agit d’une caténoïde, dont l’axe central du tube a la forme d’une chaînette : la tension à la surface supérieure du tube caténoïde (exercée longitudinalement dans la direction de l’axe du tube) est inférieure à celle de la surface inférieure et explique pourquoi le tube d’eau se rompt toujours par le bas quand cette tension d'écartement devient supérieure à la tension de rapprochement exercée entre les molécules savonneuses.
Cette question de la surface minimale, a été posée et résolue par le mathématicien et physicien suisse Leonhard Euler, en 1744.
Le caténoïde est pourtant la forme idéale à adopter pour une structure autoportée adoptant un profil de chaînette car il est possible de compenser les forces de compression exercées à la surface supérieure par une précompression de cette surface, et de compenser les forces d'écartement à la surface inférieure du tube en lui permettant une plus grande élasticité. Cette forme est donc adoptée pour les tubes d'arches porteuses.
La chaînette d'égale résistance
La chaînette d'égale résistance est la forme prise par un fil pesant flexible inextensible suspendu entre 2 points, dont la surface de section transversale est amenée à varier le long de sa longueur pour être partout proportionnelle à la tension locale, de manière à obtenir une contrainte uniforme de traction dans la chaîne ou le câble.
Cette courbe est dite aussi, « chaînette de Coriolis », ou « courbe du log sinus », et a été étudiée par l'ingénieur anglais Davies Gilbert (en) (« catenary of equal strength »), en 1826.
En France, elle sera étudiée par le mathématicien Gustave Coriolis, dans une note publiée en 1836, dans le Journal de mathématiques pures et appliquées.
La chaînette élastique

La chaînette élastique est la forme prise par un fil pesant flexible infiniment mince homogène élastique suspendu entre deux points, placé dans un champ de pesanteur uniforme.
Cette courbe a été étudiée, par le mathématicien et géomètre Étienne Bobillier, en 1826, et le mathématicien M. Finck.
Autres applications : les ponts
Le pont non suspendu
Un pont non suspendu constitué d'une seule arche quasi plane et porté uniquement à ses deux extrémités, adopte naturellement une forme de chaînette s’il n'est soumis à aucune autre contrainte verticale ou horizontale que son propre poids ou si la charge qu'il supporte est distribuée équitablement le long de sa longueur. Il en est de même pour une charpente horizontale posée à cheval entre deux murs porteurs.
Le pont de singe
Pont de singe rudimentaire à double balustrade en corde, non loin du glacier Briksdalsbreen, en Norvège
Le pont de singe, adopte naturellement la forme d'une chaînette, à cause d'un tablier, réduit à la plus simple expression, comme par exemple, près du glacier Briksdalsbreen, en Norvège.
Le pont caténaire
Pont suspendu pour piétons, à Holzgau, Tyrol, Autriche, il est composé d'un tablier et de deux balustrades soutenus par des haubans, le tout en éléments métalliques
Le pont caténaire piétonnier, structure proche du pont de singe, adopte lui aussi la forme de la chaînette, comme par exemple le pont suspendu pour piétons d'Holzgau (de), construit en 2012, à Holzgau, au Tyrol, en Autriche.
Le pont autoporté
D'autres systèmes existent dans la construction de ponts autoportés (construits comme une arche en chaînette renversée), leur permettant de résister à d’autres contraintes exercées soit horizontalement perpendiculairement aux arches ou câbles porteurs dans l’axe du pont (essentiellement par le vent) ou verticalement sur la surface du pont (soit par le vent soit par les véhicules qui y circulent : cette contrainte est plus facile à contrôler car elle a un effet identique à une variation de son poids propre et conduit à raccourcir la longueur de portée) ; ceci nécessite que les extrémités du pont puissent se déplacer horizontalement, afin d'éviter la rupture au centre du pont par augmentation de la tension longitudinale si on empêche ce déplacement longitudinal qui permet de conserver le profil idéal de chaînette), et peut être réalisé par des zones à chaque extrémité coulissant librement l'une dans l'autre dans l’axe du pont; la surveillance permanente de l'écartement ou du rapprochement de ces zones coulissantes permet de mesurer instantanément la tension longitudinale de la structure autoportée et donc de prévenir les ruptures (ou de fermer la circulation dès que des seuils de sécurité sont dépassés par exemple à cause de vents trop violents). Le même système est employé pour les charpentes horizontales, légèrement plus longues que l'écartement des murs ou pylônes verticaux porteurs, et parfois portées par un bras rotatif articulé au sommet du pylône porteur permettant d'équilibrer l'écartement à chaque extrémité.


悬链线是一种常用曲线,物理上用于描绘悬在水平两点间的因均匀引力作用下的软绳的形状,因此而得名。它的公式为:
-
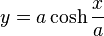 或者简单地表示为
或者简单地表示为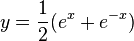
其中cosh是双曲余弦函数, 是一个由绳子本身性质和悬挂方式决定的常数,轴为其准线。具体来说,,其中是重力加速度,是线密度(假设绳子密度均匀),而是绳子上每一点处张力的水平分量,它取决于绳子的悬挂方式;若绳子两端在同一水平面上,则下面的方程决定了
其中L是绳子总长的一半,d是端点距离的一半。
方程的推导
表达式的证明
如右图,设最低点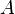 处受水平向左的拉力
处受水平向左的拉力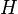 ,右悬挂点处表示为
,右悬挂点处表示为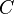 点,在
点,在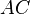 弧线区段任意取一段设为
弧线区段任意取一段设为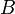 点,则B受一个斜向上的拉力
点,则B受一个斜向上的拉力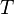 ,设
,设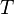 和水平方向夹角为
和水平方向夹角为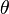 ,绳子的质量为
,绳子的质量为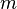 ,受力分析有: 注释 注释
,受力分析有: 注释 注释
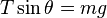 ;
;
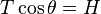 ,
,
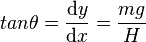 ,
,
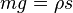 , 其中
, 其中 是右段
是右段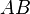 绳子的长度,
绳子的长度, 是绳子线重量密度,代入得微分方程
是绳子线重量密度,代入得微分方程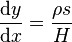 ;利用弧长公式
;利用弧长公式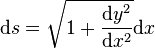 ;所以
;所以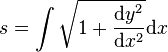 ;
;
所以把 代入微分方程得
代入微分方程得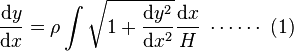
对于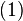 设
设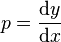 微分处理
微分处理
得 
 ;
;
对(2)分离常量求积分
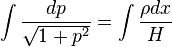
得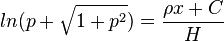 ,即asinhp(反双曲正弦)=
,即asinhp(反双曲正弦)=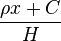
当x=0时,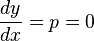 ;带入得C=0;
;带入得C=0;
整理得asinhp=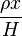 另祥解:(
另祥解:(![\ln[p+\sqrt{1+p^2}]=\frac{\rho x}{H}](https://wiki-gateway.eudic.net/wikipedia_zh/I/m/53eaba71b82c62a7faad06c59e859ea8.png) );
);
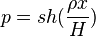 (
(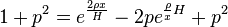 );
);
(![p=[e^(\frac{\rho x}{H})-e^(-\frac{\rho x}{H})]/2=\frac{dy}{dx}](https://wiki-gateway.eudic.net/wikipedia_zh/I/m/4512b67d41734dc5d153f7799de80f42.png) );
);
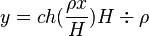 (
(![y=\frac{H}{2\rho}e^{\frac{\rho x}{H}}+e^{\frac{\rho x}{H}}]](https://wiki-gateway.eudic.net/wikipedia_zh/I/m/bbb323877dc41dc38b8a5c24dc163606.png) );
);
令a=H/ρ: y=a*cosh (x/a)
(y=a[e^(x/a)+e^(-x/a)]/(2)= a*cosh(x/a))。
工程中的应用
悬索桥、双曲拱桥、架空电缆都用到悬链线的原理。 在工程中有一种应用,称作悬链系数。如果我们改变公式的写法,会给工程应用带来很大帮助,公式及图像如下: 还有以下几个公式,可能也有用: 其中是曲线中某点到0点的链索长度,是该点的正切角,是0点处的水平张力,是链索的单位重量。利用上述公式即能计算出任意点的张力。

 词典释义:
词典释义:
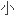
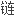





 线
线 状针迹,
状针迹,  状线圈
状线圈
 ;
; 绳;
绳;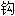 ,扣环;
,扣环;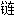 ,颈饰;
,颈饰;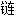 线
线