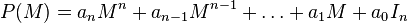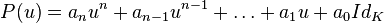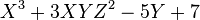Courbe représentative d'une fonction cubique (en).
En mathématiques, un polynôme est une expression formée uniquement de produits et de sommes de constantes et d'indéterminées, habituellement notées X, Y, Z… Ces objets sont largement utilisés en pratique, ne serait-ce que parce qu'ils donnent localement une valeur approchée de toute fonction dérivable (voir développement limité) et permettent de représenter des formes lisses (voir l'article courbe de Bézier, décrivant un cas particulier de fonction polynôme).
Un polynôme, en algèbre générale, à une indéterminée sur un anneau (unitaire) est une expression de la forme :
où X est un symbole appelé indéterminée du polynôme, supposé être distinct de tout élément de l'anneau, les coefficients sont dans l'anneau, et est un entier naturel.
Si, en mathématiques appliquées, en analyse et en algèbre linéaire, il est fréquent de confondre le polynôme avec la fonction polynôme, il n'en est pas de même en algèbre générale. Cet article traite principalement du polynôme formel à une indéterminée.
Considérations historiques
L'histoire des polynômes est inséparable de celle de l'algèbre. Initialement créés pour résoudre des équations, ils se trouvent confondus avec les fonctions polynômes. Au fur et à mesure que les recherches s'approfondissent, il se révèle nécessaire de distinguer plus nettement le polynôme formel de la fonction polynôme. Cette évolution se fait conjointement avec le développement de l'algèbre générale. Les coefficients quittent alors le domaine des nombres usuels, comme les réels ou les complexes, pour appartenir à des anneaux commutatifs unitaires ou à des corps commutatifs quelconques. L'étude des polynômes formels ouvre la porte à celle des séries formelles.
Polynômes formels
Un polynôme f à une indéterminée est défini comme une expression formelle de la forme
où les coefficients a0, .., an sont éléments d'un anneau A, et X est un symbole formel appelé indéterminée du polynôme.
Plus formellement, on peut définir un polynôme comme une suite d'éléments, d'un anneau, qui s'annule à partir d'un certain rang. Ainsi, la formule précédente sera une conséquence immédiate (en faisant recours à des notations mathématiques classiques à savoir la notation de Kronecker). Dans ce cas, les coefficients du polynôme coïncident avec les éléments de la suite associée.
L'ensemble des polynômes à une indéterminée X à coefficients dans un anneau A, noté A[X], peut être construit à partir de l'ensemble des suites à support fini (donc nulles à partir d'un certain rang, appelées également suites presque nulles) d'éléments de A, en le munissant d'une structure d'anneau. Dans cette construction un terme aX est représenté par la suite qui est nulle partout, sauf que .
Le degré de ce polynôme est défini, si le polynôme est non nul (c'est-à-dire si ses coefficients ne sont pas tous nuls), par , c'est le plus grand exposant de X devant lequel le coefficient n'est pas nul. On note généralement le degré d'un polynôme P, deg(P) ou d°(P). Par convention, le degré du polynôme nul vaut −∞.
Deux polynômes sont égaux si et seulement si les suites de leurs coefficients sont égales. Les polynômes à coefficients dans A peuvent être ajoutés simplement par l'addition des coefficients correspondants, et multipliés en utilisant la distributivité de la multiplication par rapport à l'addition et la règle suivante :
aX bX = ab X pour tous les entiers naturels j et k.
On peut alors vérifier que l'ensemble de tous les polynômes à coefficients dans l'anneau A forme lui-même un anneau, et que l'application de A vers cet anneau qui envoie a sur a X est un morphisme injectif. L'anneau des polynômes à coefficients dans A est noté A[X] et on considère A comme sous-anneau de A[X] par le morphisme mentionné.
Si A est commutatif, alors A[X] est une algèbre associative sur A.
On peut engendrer l'anneau A[X] à partir de A en adjoignant un nouvel élément X à A et en exigeant que X commute avec tous éléments de l'ensemble A. Pour que l'ensemble obtenu devienne un anneau, toutes les combinaisons linéaires de puissances de X doivent être aussi adjointes à l'ensemble.
Fonctions polynômes
À tout polynôme P(X) de A[X], on peut associer une fonction polynôme, d'ensemble de définition et d'arrivée A. On obtient la valeur de cette fonction pour un argument donné x en remplaçant partout le symbole X dans P(X) par x. Les algébristes font une distinction entre un polynôme et une fonction polynomiale car, sur certains anneaux A (par exemple sur les corps finis), deux polynômes différents peuvent avoir la même fonction polynôme associée. Ceci n'est pas le cas sur le corps des réels ou des complexes et donc les « analystes » ne séparent pas les deux concepts.
Exemple : Sur le corps fini ℤ/2ℤ, le polynôme X + X est non nul, mais sa fonction polynôme associée l'est.
Morphisme d'évaluation : plus généralement, dans un polynôme P(X), on peut remplacer le symbole X par n'importe quel élément e appartenant à une algèbre associative E sur A. L'application qui, à tout polynôme P(X) dans A[X], associe l'élément P(e) de E (défini comme ci-dessus), est appelée morphisme d'évaluation en e de A[X] dans E. Un cas très fréquent est celui où A est un corps K, et E l'algèbre des matrices n × n sur K, ou bien l'algèbre des endomorphismes d'un espace vectoriel sur K. On définit ainsi des polynômes de matrices et d'endomorphismes :
Ainsi, pour tout polynôme P(X), d'indéterminée X, P(u) est un « polynôme d'endomorphisme » pour chaque endomorphisme u et P(M) est un « polynôme de matrice » pour chaque matrice M.
Divisibilité
En algèbre commutative, et plus précisément dans un anneau intègre (toujours commutatif et unitaire par définition), une attention particulière est portée sur l'étude de la divisibilité entre les polynômes. Des résultats plus forts existent quand les coefficients sont pris dans un corps.
Coefficients dans un anneau intègre
Si f et g sont des polynômes dans A[X], on dit que f divise g s'il existe un polynôme q dans A[X] tel que fq = g.
On peut démontrer alors que « chaque racine engendre un facteur linéaire », ou plus formellement que : si P est un polynôme dans A[X] et a est un élément de A tel que P(a) = 0, alors le polynôme X – a divise P (la réciproque est immédiate). Le quotient peut être calculé en utilisant la méthode de Horner.
Certains polynômes aux propriétés particulières se détachent alors :
Polynôme inversible : un polynôme P est inversible s'il existe un polynôme Q tel que PQ = 1. Les seuls polynômes inversibles de A[X] sont les polynômes constants dont la constante est inversible dans A ;
Polynôme irréductible : P est un polynôme irréductible s'il n'est ni nul, ni inversible, ni produit de deux polynômes non inversibles. Un polynôme du premier degré aX + b est donc irréductible si et seulement si a et b sont premiers entre eux (par exemple, tout polynôme unitaire du premier degré est irréductible, tandis que 2X + 2 = 2(X + 1) n'est pas irréductible dans ℤ[X]). Le polynôme X + 1 est irréductible dans ℝ[X], mais pas dans ℂ[X]. Si A est un anneau factoriel, alors tout polynôme se décompose de manière unique, à un inversible près, en produit de polynômes irréductibles. A[X] est donc aussi factoriel ;
Polynôme premier : P est un polynôme premier s'il n'est ni nul ni inversible et si, pour tout produit QS divisible par P, l'un des deux polynômes Q ou S est divisible par P. Dans un anneau factoriel (donc dans A[X] si A est factoriel), les notions d'élément premier et d'élément irréductible sont équivalentes mais dans un anneau quelconque, on a seulement la propriété suivante : tout élément premier est irréductible ;
Polynôme primitif : si A est un anneau factoriel, P est un polynôme primitif si le PGCD de ses coefficients est inversible. Dans un anneau commutatif unitaire, un polynôme est dit primitif lorsque l'anneau est le plus petit idéal principal contenant les coefficients du polynôme ;
Polynôme scindé : polynôme qui peut s'écrire comme produit de polynômes du premier degré. X + 1 est scindé sur ℂ (il se décompose en (X + i)(X – i)) mais pas sur ℝ ;
Polynôme séparable (sur un corps) : polynôme étant premier avec son polynôme dérivé ;
Polynômes premiers entre eux : P et Q sont premiers entre eux si les seuls polynômes qui divisent à la fois P et Q sont les polynômes inversibles ;
Polynôme unitaire : polynôme dont le coefficient du terme de plus haut degré est 1 ;
Polynôme cyclotomique : pour tout entier n > 0, le n-ième polynôme cyclotomique est le produit des X – ζ avec ζ parcourant les racines complexes n-ièmes primitives de l'unité.
Coefficients dans un corps commutatif
Si K est un corps commutatif et f et g sont des polynômes dans K[X] avec g ≠ 0, alors il existe des polynômes q et r dans K[X] avec : f = q g + r et tels que le degré de r soit strictement plus petit que le degré de g. Les polynômes q et r sont uniquement déterminés par f et g. C'est ce que l'on appelle la division euclidienne ou «la division suivant les puissances décroissantes» de f par g et cela montre que l'anneau K[X] est un anneau euclidien.
K[X] est donc un anneau euclidien (seuls les anneaux de polynômes à coefficients dans un corps sont des anneaux euclidiens) et cela permet alors de définir les notions de PPCM, de PGCD avec la mise en place d'un algorithme d'Euclide de recherche de pgcd. On retrouve aussi l'identité de Bézout sur les polynômes premiers entre eux : si P et Q sont premiers entre eux, il existe deux polynômes U et V tels que UP + VQ = 1.
Réductibilité des polynômes de Z[X]
Un polynôme primitif A de ℤ[X] est irréductible si et seulement si, considéré comme polynôme de ℚ[X], il est irréductible dans ℚ[X]. De plus si A = BC dans ℚ[X], il existe un rationnel non nul λ tel que λB et λC soient dans ℤ[X].
Remarque : Si des polynômes A, B, C de ℤ[X] vérifient A = BC et si A est unitaire alors B et C sont également unitaires (au signe près).
Constructions de nouvelles structures
Elles sont de deux types : extensions de l'anneau A[X] ou de l'anneau A de départ.
Corps des fractions
Si A est un anneau intègre (donc commutatif et unitaire), il en est de même de son anneau de polynômes ; on peut donc construire le corps des fractions de A[X], appelé corps des fractions rationnelles à coefficients dans A et d'indéterminée X.
Corps de rupture
La seconde structure conduit à tout le domaine des extensions.
Si A est un anneau intègre et si P est un polynôme premier de A[X], on peut construire un anneau intègre AP contenant A dans lequel P possède une racine. Lorsque A est un corps, AP aussi : c'est le corps de rupture de P.
La construction se fait en considérant l'idéal I engendré par P. C'est un idéal premier de A[X], et même un idéal maximal si A est un corps. L'anneau quotient A[X]/I est donc un anneau intègre, et même un corps si A en est un.
On plonge alors A dans cet anneau AP par le morphisme injectif qui à tout élément associe sa classe. Si l'on note r la classe de X alors P(r) est la classe de P. Comme P est dans l'idéal I, sa classe est nulle donc P(r) = 0.
Il est possible de réitérer ce processus jusqu'à obtenir un corps contenant toutes les racines. Ce corps s'appelle le corps de décomposition.
Un corps est algébriquement clos quand il est inutile de chercher des corps de rupture, c'est-à-dire quand tous les polynômes sont scindés. C'est le cas en particulier de ℂ.
Autres opérations sur les polynômes
Polynôme dérivé
Sur A[X], si P est le polynôme défini par le polynôme dP défini par s'appelle le polynôme dérivé de P (en particulier, da0 = 0).
L'application d de A[X] dans A[X] est un morphisme de modules (et donc de groupes), vérifiant de plus d(PQ) = PdQ + QdP. À ce titre, c'est une application de dérivation.
Une propriété importante du polynôme dérivé est le fait qu'une racine est multiple si et seulement si elle est aussi racine du polynôme dérivé. (Pour une démonstration et des énoncés plus précis, voir le § « Critère différentiel pour la multiplicité d'une racine » de l'article Racine d'un polynôme.)
Division
Si K est un corps commutatif, l'anneau K[X] dispose de deux divisions. La première est euclidienne et confère à l'ensemble des polynômes une structure d'anneau euclidien permettant d'y développer une arithmétique des polynômes un peu analogue à celle des entiers. Cette arithmétique s'avère importante pour la factorisation des polynômes. La deuxième est dite selon les puissances croissantes. Elle est utile dans la recherche d'une décomposition en éléments simples d'une fraction rationnelle ou d'un développement limité.
Polynôme en plusieurs indéterminées
Le cas de ces polynômes sera juste évoqué ici car l'anneau A[X, Y] peut simplement être considéré comme l'anneau des polynômes de la variable Y à coefficients dans A[X].
Le degré du polynôme sera alors la plus grande valeur obtenue en faisant les somme des exposants de chaque indéterminée dans chaque monôme.
est un polynôme de degré 4 à trois indéterminées.
Parmi les polynômes à n indéterminées, l'étude des polynômes symétriques et de leur groupe de permutations est un domaine important de l'algèbre.
Ces polynômes sont également dits multivariés, par opposition aux polynômes univariés, à une seule variable.
Polynôme de Laurent
Il est également possible d'introduire les puissances négatives d'une variable et d'obtenir ainsi un anneau A[X, X] dit de Laurent. C'est l'algèbre du groupe ℤ sur l'anneau A.
多项式是代数学中的基础概念,是由称为不定元的变量和称为系数的常数通过有限次加减法、乘法以及自然数幂次的乘方运算得到的代数表达式。例如X - 3X + 4就是一个多项式。多项式是整式的一种。不定元只有一个的多项式称为一元多项式;不定元不止一个的多项式称为多元多项式。
多项式在数学的很多分支中乃至许多自然科学以及工程学中都有重要作用。
定义
给定一个环 R(R 通常是交换环,可以是有理数、实数或者复数等等)以及一个不定元 X,则任何形同: 的代数表达式叫做 R 上的一元多项式。其中 a0, …, an 是R 中的元素。不定元不代表任何值,但环R上的所有运算都对它适用。在不至于混淆的情形下,一般将一元多项式简称为多项式。可以证明,两个多项式的和、差与积仍然是多项式,即多项式组成一个环 R[X],称为 R 上的(一元)多项式环。而所有的二元多项式则可以定义为所有以一元多项式为系数的多项式,即形同 的代数表达式。其中都是 R[X1] 中的元素。全体这样的表达式也构成一个环,记为R[X1, X2]。以此类推,可以定义所有m元多项式集合:R[X1, X2, ... , Xm] 多项式总可以表示为有限个元素的和,其中每个元素都是不定元与R中一个常数的乘积,这样的元素称为多项式的项,其中的常数称为该项的系数。在 中,多项式的每一项都是形同的乘积形式。其中a 是系数,ki被称为Xi在这一项中的次数。所有ki之和称为这一项的次数。比如在以下这一项: 中,系数是-5,不定元X的次数是3,Y的次数是1,这一项的次数是4. 可以写成只由一项构成的多项式也称为单项式。如果一项中不含不定元,则称之为常数项。 次数 某个不定元Xs在多项式各项中最大的次数称为多项式中不定元Xs的次数,拥有这样次数的Xs的项被称为Xs的最高次项。所有项的次数中最高的称为多项式的次数。对于一元多项式来说,唯一的不定元的次数也称为多项式的次数,不定元的最高次项也称为多项式的最高次项。 例如多项式: 中 的次数最高,是4,故此多项式的次数为四。 因而此多项式可称为三元四次四项式。称为四次项,、 称为一次项或线性项,而 5 是零次项或常数项。 多项式 P 的次数记作 deg(P)。约定零多项式没有次数,也没有不定元。常数多项式分为零次多项式(非零常数)和零多项式。一次多项式又称为 线性多项式。多项式中的一次项又称为线性项。如果某个多项式的所有项都有相同次数,则称其为齐次多项式。 一个一元多项式被称为首一多项式,如果它的最高次项的系数是R的单比特。 多项式的升幂及降幂排列 选定一个不定元后,多项式可依各项中该不定元的次数以降序或升序排列。次数从低到高是升幂排列。次数从高到低是降幂排列。例如 是依X的次数降幂排列。而 则是以Y的次数升幂排列。
多项式的运算
多项式的加法 两个多项式相加可以看作是对两组单项式的和进行重组与合并同类项。通过加法结合律,可以将同类项放在一起,合并之后就得到了两个多项式的和。例如以下的两个多项式: 它们的和是: 化简之后得到: 多项式乘法 计算两个多项式相乘时,首先使用乘法对加法的分配律将各项拆出,然后运用乘法结合律集成每一项,最后和加法一样集成同类项,就能得到乘积多项式。例如以下的两个多项式: 计算它们的乘积,步骤如下: 化简之后得到: 多项式除法 和整数之间的带余除法类似,一元多项式之间也可以进行带余除法。可以证明,设有多项式A和非零多项式B,则存在唯一的多项式Q和R,满足: 并且多项式R要幺是零多项式,要幺其次数严格小于B的次数。 作为特例,如果要计算某个多项式P除以一次多项式X - a得到的余多项式,可以直接将a带入到多项式P中。P除以X - a的余多项式是P (a)。 具体的计算可以使用类似于竖式除法的方式。例如,计算除以,列式如下: 因此,商是,余式是。
多项式的矩阵算法
乘法
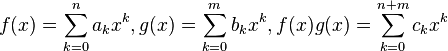
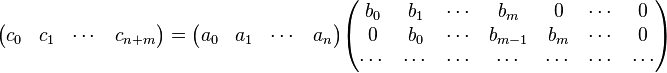
除法
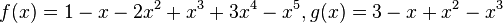 ,f(x)除以g(x)
,f(x)除以g(x)
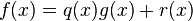 ,应用多项式乘法的矩阵算法
,应用多项式乘法的矩阵算法
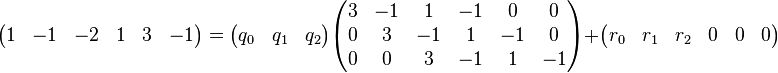
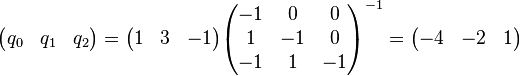
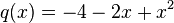
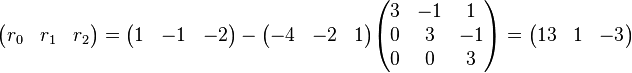
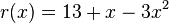
因式分解
因式分解是指把一个多项式分解成几个(非常数的)多项式的乘积。其中的每一个多项式称为原多项式的因式。因式分解有助于理解多项式的性质,比如根的分布等等。因式分解的结果通常和多项式所在的系数域有关。如果要求因式分解后的每一个因式都在一定的系数域(比如有理数域)里面,那幺结果可能和要求它们在另一个系数域(比如说复数域)里不同。比如多项式在有理数域内分解为: 在实数域内则可以进一步分解为: 在复数域内还可以再进一步分解: 如果给定了系数域,那幺在不考虑因式排列顺序的情况下,因式分解是唯一的。如果(在给定的系数域上,)一个多项式不能被表示为次数严格比它低的多项式的乘积,就称它为不可约多项式。因式分解一般是指将多项式分解到不可再分的多项式乘积,也就是不可约多项式的乘积,否则称其为不完全的因式分解。 对于一元多项式来说,所有复系数多项式都可以分解成若干个一次因式的乘积,这个结论等价于代数基本定理。所有实系数多项式都可以分解为次数不超过二次的多项式的乘积。比较复杂的是有理数系数多项式的因式分解。首先,给定一个有理系数多项式P,可以将其乘以一个特定的有理数c,将其变成一个整系数多项式,所以有理系数多项式和整系数多项式的因式分解是等价的。如果一个整系数多项式各项系数的最大公约数是1,就称其为本原多项式。不是本原多项式的整系数多项式P,假设其各项系数的最大公约数是d,那幺可以将P的因式分解问题转化为本原多项式P/d的因式分解问题。所以有理数系数和整系数多项式的因式分解都等价于本原多项式的因式分解问题。利用本原多项式可以证明:整系数多项式如果能分解为有理系数多项式的乘积,那幺也必然能分解成整系数多项式的乘积。艾森斯坦判别法给出了判定整系数多项式不可约的充分条件。另一个常用的准则与多项式的最高次项系数与常数项系数有关。如果某个多项式有某个有理数根(既约形式),那幺分子p 必然整除常数项系数a0,而分母q 也必然整除最高次项系数an。
多项式函数
多项式函数是指给多项式中的不定元赋值的映射。比如说一元多项式函数的普遍形式为: 其中的是一个代数,可以是有理数、实数或复数。多项式函数是函数而不是多项式,但多项式函数之间也可以进行像多项式一般的加法、乘法运算,其结果仍旧是多项式函数。所以所有的多项式函数也构成一个环,而且这个环显然和多项式环同构。 与多元多项式对应的也有多元多项式函数。比如就是一个与二元多项式对应的二元多项式函数。 所有多项式函数都是光滑函数(无限可微连续函数),因此可以定义其导数、原函数等概念。另外,当每个变量都趋于无穷大(绝对值)的时候,多项式函数的值(绝对值)也趋于无穷大。 多项式方程 多项式方程是指多项式函数构成的方程。给定多项式,则对应的多项式函数可以构造方程: 例如: 就是一个多项式方程。 如果某个使得多项式方程,那幺就称为多项式方程的解,或多项式函数的一个根或零点。多项式函数的根与多项式有如下关系:如果某个是多项式函数的一个根,那幺一次多项式整除多项式,也就是说存在多项式,使得:;反之亦然。如果存在(一般来说大于1的)正整数k,使得,那幺称是多项式函数的一个k重根。 多项式的根是否存在以及根的数目取决于多项式的系数域以及指定的根所在的域。代数基本定理说明,复系数多项式在复数域内必然有至少一个根。这可以推出,n次多项式函数必定有n个根。这里说的n个根指包括了重根的情况。另外可以证明,奇数次实系数多项式在实数域内至少有一个根。
字典排列法
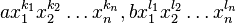 是两个不同的项
是两个不同的项
若存在i使得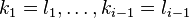 ,但
,但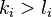 ,则
,则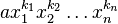 在
在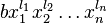 前
前
例如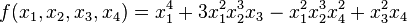 ,这种排列法称为字典排列法。
,这种排列法称为字典排列法。
多项式的分析特性
多项式函数在分析学中有重要的作用。由于多项式函数有简洁明确的形式,很容易对其进行量化分析。比如,多项式函数 它的导函数是: 它的原函数(族)是: 这个定义可以类比到多项式本身,令多项式中也定义导数的概念。多项式的导数多项式是: 它的积分多项式则是: 一个n次多项式(n大于等于1)的导数多项式是一个n-1次多项式。常数多项式的导数多项式是零多项式。它的积分多项式则是一个n+1次多项式。和分别称为多项式的微分算子和积分算子。
任意环上的多项式
多项式可以推广到系数在任意一个环的情形,请参阅条目多项式环。

 词典释义:
词典释义:
 词:
词:
 词:
词:
 ;
; 量的, 矢量的;
量的, 矢量的;