En informatique et en logique, un problème d'unification est un système d'équations qui portent sur des termes. Par exemple, est un problème d'unification (avec une seule équation). L'unification a des applications en programmation logique, en système de réécriture. Souvent, on s'intéresse à l'unification syntaxique où il faut que les membres gauche et droit des équations sont syntaxiquement égaux. Par exemple, la solution de est car on lit de part et d'autre de l'équation. Par contre, le problème d'unification syntaxique n'a pas de solution ː attention, n'est pas une solution car les termes et sont syntaxiquement différents.
Histoire
Le premier chercheur à évoquer un algorithme d'unification est Jacques Herbrand dans sa thèse, mais en fait l'unification a été redécouverte par John Alan Robinson dans le cadre de sa méthode de résolution en démonstration automatique. C'est lui qui lui donna son nom actuel. Une étape importante est ensuite la découverte d'algorithmes linéaires par Martelli et Montanari, Paterson et Wegman et Huet. Prolog a aussi beaucoup contribué à sa popularisation. Des algorithmes spécifiques pour les termes de certaines théories, appelés aussi unification équationnelle (en particulier associative et commutative par Stickel) ont été proposés (voir ci-dessus).
Quelques exemples
Le problème d'unification  a une solution
a une solution 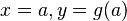 car substituer (i.e. remplacer) le terme
car substituer (i.e. remplacer) le terme 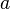 à la variable
à la variable  et le terme
et le terme 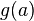 à la variable
à la variable 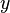 , dans les deux termes
, dans les deux termes 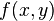 et
et 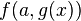 donne le même terme
donne le même terme 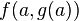 .
.
Le problème d'unification 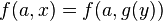 a une infinité de solutions ː
a une infinité de solutions ː
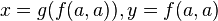
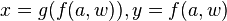
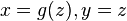 etc.
etc.
En revanche, le problème d'unification 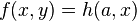 n'a pas de solution et le problème d'unification
n'a pas de solution et le problème d'unification 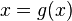 non plus.
non plus.
Solution principale
Une solution 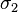 d'un problème d'unification est dite plus générale qu'une solution
d'un problème d'unification est dite plus générale qu'une solution 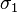 , si
, si 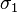 est obtenue en substituant des termes à des variables dans
est obtenue en substituant des termes à des variables dans 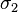 .
.
Par exemple, si on considère le problème d'unification
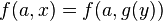
alors la solution
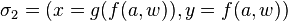
est plus générale que la solution

qui est obtenue en substituant le terme 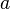 à la variable
à la variable 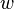 dans
dans 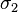 . De même, la solution
. De même, la solution
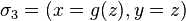
est plus générale que la solution 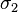 , qui est obtenue en substituant le terme
, qui est obtenue en substituant le terme 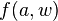 à la variable
à la variable 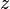 dans la solution
dans la solution  .
.
Une solution 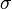 d'un problème d'unification est dite principale si elle est plus générale que toutes les solutions de ce problème, c'est-à-dire si toute solution est obtenue en substituant des termes à des variables dans
d'un problème d'unification est dite principale si elle est plus générale que toutes les solutions de ce problème, c'est-à-dire si toute solution est obtenue en substituant des termes à des variables dans 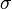 .
.
Dans cet exemple, la solution  est une solution principale du problème
est une solution principale du problème
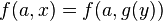
Le théorème de la solution principale exprime que si un problème d'unification a une solution, alors il a une solution principale.
Algorithme de Robinson pour l'unification syntaxique
L'algorithme de Robinson permet de décider si un problème d'unification a des solutions ou non et, quand il en a, de calculer une solution principale.
On choisit une équation dans le système.
Si cette équation a la forme
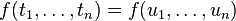
on la remplace par les équations 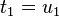 , ...,
, ..., 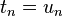 et on résout le système obtenu.
et on résout le système obtenu.
Si cette équation a la forme
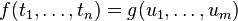
où 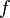 et
et 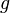 sont des symboles différents, on échoue.
sont des symboles différents, on échoue.
Si cette équation a la forme

on la supprime du système et on résout le système obtenu.
Si cette équation a la forme
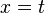
ou
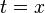
où  apparaît dans
apparaît dans  et est distinct de
et est distinct de  , on échoue.
, on échoue.
Si cette équation a la forme
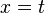
ou
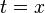
et que  n'apparaît pas dans
n'apparaît pas dans  , on substitue le terme
, on substitue le terme  à la variable
à la variable  dans le reste du système, on résout le système obtenu, ce qui donne une solution
dans le reste du système, on résout le système obtenu, ce qui donne une solution 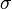 et on retourne la solution
et on retourne la solution 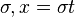 .
.
Filtrage
Un problème de filtrage est un problème d'unification dans lequel, dans chaque équation, les variables n'apparaissent que dans le terme de gauche. Par exemple, le problème
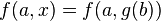
est un problème de filtrage, car le terme 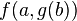 ne contient pas de variables.
ne contient pas de variables.
Dans le cas du filtrage, l'algorithme de Robinson se simplifie.
On choisit une équation dans le système.
Si cette équation a la forme
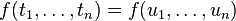
on la remplace par les équations 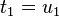 , ...,
, ..., 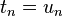 et on résout le système obtenu.
et on résout le système obtenu.
Si cette équation a la forme
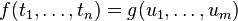
où 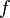 et
et 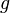 sont des symboles différents, on échoue.
sont des symboles différents, on échoue.
Si cette équation a la forme
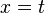
on substitue le terme  à la variable
à la variable  dans le reste du système, on résout le système obtenu, ce qui donne une solution
dans le reste du système, on résout le système obtenu, ce qui donne une solution 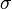 et on retourne la solution
et on retourne la solution 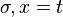 .
.
Utilisation de l'unification et du filtrage dans les langages de programmation
L'unification est ce qui distingue le plus le langage de programmation Prolog des autres langages de programmation.
En Prolog, l’unification est associée au symbole « = » et ses règles sont les suivantes :
une variable X non-instanciée (c'est-à-dire ne possédant pas encore de valeur) peut être unifiée avec une autre variable (instanciée ou pas); les deux variables deviennent alors simplement des synonymes l'une de l'autre et représenteront dorénavant le même objet (ou la même structure) ;
une variable X non-instanciée peut être unifiée avec un terme ou un atome et représentera dorénavant ce terme ou atome ;
un atome peut être unifié seulement avec lui-même ;
un terme peut être unifié avec un autre terme : si leurs noms sont identiques, si leur nombres d'arguments sont identiques et si chacun des arguments du premier terme est unifiable avec l'argument correspondant du second terme.
En raison de sa nature déclarative, l'ordre dans une suite d'unifications ne joue aucun rôle.
Exemples d'exécution de l'unification en Prolog
On suppose que toutes les variables (en majuscules) sont non-instanciées.
A = A
-
réussit (réflexivité)
A = B, B = abc
-
A et B représentent alors l'atome 'abc'
xyz = C, C = D
-
réussit: l'unification est symétrique
abc = abc
-
réussit: les atomes sont les mêmes.
abc = xyz
-
échoue: des atomes distincts ne s'unifient pas
f(A) = f(B)
-
réussit: A est unifié avec B
f(A) = g(B)
-
échoue: les termes ont des noms différents
f(A) = f(B, C)
-
échoue: les termes ont un nombre d'arguments différent
f(g(A)) = f(B)
-
réussit: B est unifié au terme g(A)
f(g(A), A) = f(B, xyz)
-
réussit: A est unifié à l'atome 'xyz' et B est unifié au terme g(xyz)
A = f(A)
-
l'unification est infinie: A est unifié au terme f(f(f(f(f(...)))). Suivant le système logique utilisé, l'unification échoue ou réussit; pour la plupart des systèmes, l'unification échoue.
A = abc, xyz = X, A = X
-
échoue: car abc=xyz échoue
Autres algorithmes pour l'unification syntaxique
Algorithme de Herbrand (redécouvert par Martelli et Montanari)
L'algorithme de Herbrand est redécouvert par Martelli et Montanari (1982). On se donne un ensemble fini d'équations G = { s1 ≐ t1, ..., sn ≐ tn } où les si et ti sont des termes du premier ordre. L'objectif est de calculer une substitution la plus générale. On applique les règles suivantes à l'ensemble G jusqu'à épuisement :
| G ∪ { t ≐ t } |
⇒ |
G |
|
supprimer |
| G ∪ { f(s1,...,sk) ≐ f(t1,...,tk) } |
⇒ |
G ∪ { s1 ≐ t1, ..., sk ≐ tk } |
|
décomposer |
| G ∪ { f(t⃗) ≐ x } |
⇒ |
G ∪ { x ≐ f(t⃗) } |
|
échanger |
| G ∪ { x ≐ t } |
⇒ |
G{x↦t} ∪ { x ≐ t } |
si x ∉ vars(t) et x ∈ vars(G) |
éliminer |
Les règles suivantes sont également ajoutées en guise d'optimisation :
| G ∪ { f(s⃗) ≐ g(t⃗) } |
⇒ |
⊥ |
si f ≠ g or k ≠ m |
conflit |
| G ∪ { x ≐ f(s⃗) } |
⇒ |
⊥ |
si x ∈ vars(f(s⃗)) |
vérifier (occurs-check) |
L'algorithme est en temps exponentiel et demande un espace mémoire au plus exponentiel si l'on représente les termes par leurs arbres syntaxiques. Néanmoins, on peut n'utiliser qu'un espace mémoire si on représente les termes par des graphes.
Implémentation avec des graphes
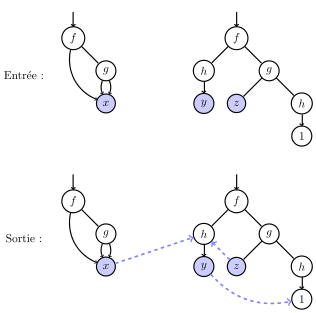
L'algorithme d'unification prend en entrée deux termes représentés par des graphes, ici f(x, g(x, x)) et f(h(y), g(z, h(1))). En sortie, une substitution la plus générale est représentée par des pointeurs (en bleu).
En implémentant l'algorithme avec des graphes, l'espace mémoire est linéaire en la taille de l'entrée même si le temps reste exponentiel dans le pire des cas. L'algorithme prend en entrée deux termes sous la forme de graphes, c'est à dire un graphe acyclique où les nœuds sont les sous-termes. En particulier, il y a un unique nœud par variables (cf. figure à droite). L'algorithme retourne en sortie une substitution la plus générale ː elle est écrite en place dans le graphe représentant les termes à l'aide de pointeurs (en bleu dans la figure à droite). C'est à dire, en plus du graphe décrivant la structure des termes (qui sont des pointeurs aussi), nous avons des pointeurs particuliers pour représenter la substitution. Par si x ː= h(1) est la substitution courante, x pointe vers le nœud correspondant au terme h(1).
Pseudo-code de l'implémentation avec des graphes
entrée ː deux termes t1, t2
sortie ː vrai si les termes sont unifiables, non sinon
fonction unifier(t1, t2)
t1 = find(t1);
t2 = find(t2);
si t1 = t2
retourner vrai;
sinon etude de cas sur (t1, t2)
(x, y):
faire pointer x vers y
retourner vrai;
(x, t) ou (t, x):
si x apparaît dans t
retourner faux
sinon
faire pointer x vers t
retourner vrai;
(f(L), g(M)):
si f = g
retourner unifierlistes(L, M)
sinon
retourner faux
où unifierListes unifient les termes de deux listes ː
entrée ː deux listes de termes L, M
sortie ː vrai si les termes des listes sont deux à deux sont unifiables, non sinon
fonction unifierlistes(L, M)
etude de cas sur (L, M)
([], [])ː retourner vrai;
([], t::t') ou (t::t', [])ː retourner faux;
(s::L', t::M'):
si unifier(s, t)
retourner unifierlistes(L', M')
sinon
retourner faux
où find trouve la fin d'une chaîne ː
entrée ː un terme t
sortie ː le terme en bout de chaîne de t
fonction find(t)
si t n'est pas une variable
retourner t
sinon
si t est déjà assigné à un terme u
retourner find(u)
sinon
retourner t
et où une implémentation naïve de "x apparaît dans t" est donné par ː
entrée ː une variable x et un terme t
sortie ː vrai si la variable x apparaît dans le terme t, non sinon
fonction apparaîtdans(x, t)
etude de cas sur t
y: retourner x = y
f(L): retourner apparaîtdansliste(x, L)
entrée ː une variable x et une liste de termes L
sortie ː vrai si la variable x apparaît dans l'un des termes de L, non sinon
fonction apparaîtdansliste(x, L)
etude de cas sur L
[]: retourner faux
t::L':
si apparaîtdans(x, find(t))
retourner vrai
sinon
retourner apparaîtdansliste(x, L')
Algorithme quadratique
L'algorithme présenté dans cette sous-section est du à Corbin et Bidoit (1983). Pour avoir une complexité quadratique, il y a deux améliorations de l'algorithme précédent.
Tester qu'une variable apparaît dans un sous-terme
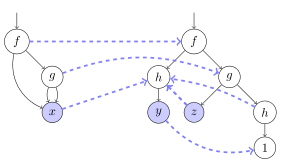
Le graphe des deux termes avec les pointeurs en bleu.
L'implémentation pour tester si une variable x apparaît dans un sous-terme t est a priori en temps exponentiel. L'idée est d'éviter de parcourir plusieurs fois les même nœuds. On marque les nœuds visités comme dans un parcours en profondeur de graphe. Une fois un test d'appartenance effectué, il faut a priori démarquer les nœuds. Au lieu de cela, on les marque avec le "temps actuel". On ajoute alors un champ aux nœuds du graphe que l'on appelle poinçon qui contient le "temps actuel". Nous disposons d'une variable globale "temps actuel" qui est incrémenté à chaque test d'appartenance.
Pseudo-code de l'implémentation du test d'appartenance entrée ː une variable x et un terme t
sortie ː vrai si la variable x apparaît dans le terme t, non sinon
fonction apparaîtdans(x, t)
temps actuel ː= temps actuel + 1
retourner apparaîtdans'(x, t)
entrée ː une variable x et un terme t
sortie ː vrai si la variable x apparaît dans le terme t, non sinon (ne change pas le temps)
fonction apparaîtdans'(x, t)
etude de cas sur t
y: retourner x = y
f(s):
si f(s) est poinçonné au temps actuel
retourner faux
sinon
poinçonner f(s) au temps actuel
retourner apparaîtdansliste(x, s)
entrée ː une variable x et une liste de termes L
sortie ː vrai si la variable x apparaît dans l'un des termes de t, non sinon
fonction apparaîtdansliste(x, L)
etude de cas sur t
[]: retourner faux
t::L':
si apparaîtdans'(x, find(t))
retourner vrai
sinon
retourner apparaîtdansliste(x, L') Éviter des appels inutiles à unifier Pour éviter des appels inutiles à la procédure qui cherche à unifier deux termes, on utilise des pointeurs pour tous les nœuds et pas seulement les variables. On peut montrer que le nombre d'appels à la procédure qui unifie est O(|A|) où |A|`est le nombre d'arcs dans le graphe. Le traitement interne utilise un parcours de pointeurs "find" en O(|S|) où |S| est le nombre de sommets et un test d'appartenance d'une variable dans un terme qui est en O(|S|̹̹̹̹̹̹̹̹̹̹̹̝+|A|) = O(|A|) car le graphe est connexe. Donc l'algorithme est bien quadratique.+ Pseudo-code de l'adaptation de la procédure d'unification entrée ː un terme t
sortie ː le terme en bout de chaîne de t
fonction find(t)
si t pointe vers un terme u
retourner find(u)
sinon
retourner t et entrée ː deux termes t1, t2
sortie ː vrai si les termes sont unifiables, non sinon
fonction unifier(t1, t2)
t1 = find(t1);
t2 = find(t2);
si t1 = t2
retourner vrai;
sinon etude de cas sur (t1, t2)
(x, y):
faire pointer x vers y
retourner vrai;
(x, t) ou (t, x):
si x apparaît dans t
retourner faux
sinon
faire pointer x vers t
retourner vrai;
(f(L), g(M)):
si f = g
faire pointer f(L) vers g(M)
retourner unifierlistes(L, M)
sinon
retourner faux Algorithme quasi-linéaire L'algorithme est inspiré de l'algorithme quadratique de la section précédente. Le test de savoir si x apparaît dans t n'est plus effectué au cours de l'algorithme mais uniquement à la fin ː à la fin, on vérifie que le graphe est acyclique. Enfin, les pointeurs de la substitution et "find" sont implémentés à l'aide d'une structure de données Union-find. Plus précisément, on conserve les pointeurs dans la structure mais on dispose en plus une structure annexe Union-find. Dans la structure de données Union-find, les classes d'équivalence ne contiennent soit que des variables soit que des termes complexes. Pour passer d'une variable à un terme complexe, on utilise les pointeurs éventuels qui sont dans le graphe. Pseudo-code de la procédure d'unification qui utilise Union-find entrée ː deux termes t1, t2
sortie ː vrai si les termes sont unifiables ou que le graphe final est acyclique, non sinon
fonction unifier(t1, t2)
t1 = find(t1);
t2 = find(t2);
si t1 = t2
retourner vrai;
sinon etude de cas sur (t1, t2)
(x, y):
Union(x, y)
retourner vrai;
(x, t) ou (t, x):
si x apparaît dans t
retourner faux
sinon
faire pointer x vers t
retourner vrai;
(f(L), g(M)):
si f = g
Union(f(L), g(M))
retourner unifierlistes(L, M)
sinon
retourner faux Construction de graphes à partir d'arbres Pour construire un graphe à partir d'un arbre, on parcourt l'arbre et on utilise une table de symboles (implémenté avec une table de hachage ou un arbre binaire de recherche) pour les variables car il faut garantir l'unicité du nœud x pour une variable x.
Unification équationnelle
Unification et logique d'ordre supérieur Lorsqu'on raisonne en logique du premier ordre, où les variables ne peuvent être unifiées qu'à des constantes, les choses se passent bien: savoir si deux termes et sont unifiables est décidable (grâce par exemple à l'algorithme ci-dessus). De plus, s'ils le sont, il existe un unificateur le plus général (most general unifier ou mgu en anglais), c'est-à-dire un terme tel que tous les autres unificateurs de et soient dérivables par instantiation de variables de . Cette situation idéale ne se retrouve hélas pas dans tous les systèmes logiques. En particulier, si on se place en logique d'ordre supérieur, c'est-à-dire qu'on s'autorise à utiliser des variables comme symboles de fonction ou comme prédicats, on perd la décidabilité et l'unicité de l'unificateur quand il existe. Au pire, deux termes peuvent même avoir une infinité d'unificateurs tous différents.

 词典释义:
词典释义:
 统一
统一 a une solution
a une solution 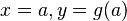 car substituer (i.e. remplacer) le terme
car substituer (i.e. remplacer) le terme 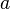 à la variable
à la variable  et le terme
et le terme 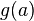 à la variable
à la variable 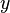 , dans les deux termes
, dans les deux termes 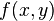 et
et 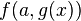 donne le même terme
donne le même terme 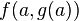 .
.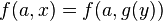 a une infinité de solutions ː
a une infinité de solutions ː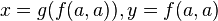
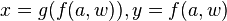
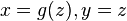
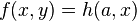 n'a pas de solution et le problème d'unification
n'a pas de solution et le problème d'unification 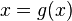 non plus.
non plus.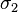 d'un problème d'unification est dite plus générale qu'une solution
d'un problème d'unification est dite plus générale qu'une solution 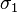 , si
, si 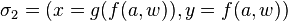

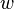 dans
dans 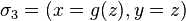
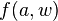 à la variable
à la variable 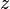 dans la solution
dans la solution  .
.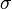 d'un problème d'unification est dite principale si elle est plus générale que toutes les solutions de ce problème, c'est-à-dire si toute solution est obtenue en substituant des termes à des variables dans
d'un problème d'unification est dite principale si elle est plus générale que toutes les solutions de ce problème, c'est-à-dire si toute solution est obtenue en substituant des termes à des variables dans 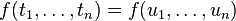
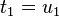 , ...,
, ..., 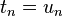 et on résout le système obtenu.
et on résout le système obtenu.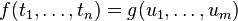
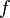 et
et 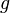 sont des symboles différents, on échoue.
sont des symboles différents, on échoue.
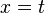
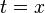
 et est distinct de
et est distinct de 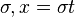 .
.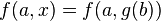
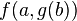 ne contient pas de variables.
ne contient pas de variables.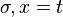 .
.
