Diffraction

La diffraction est le comportement des ondes lorsqu’elles rencontrent un obstacle ou une ouverture ; le phénomène peut être interprété par la diffusion d’une onde par les points de l'objet. La diffraction se manifeste par le fait qu'après la rencontre d’un objet, la densité de l'onde n’est pas conservée contrairement aux lois de l’optique géométrique.

La diffraction est le résultat de l'interférence des ondes diffusées par chaque point.

La diffraction s’observe avec la lumière, mais également avec le son, les vagues, les neutrons. Elle est une signature de la nature ondulatoire d'un phénomène.

Dans le domaine de l’étude des phénomènes de propagation des ondes, la diffraction intervient systématiquement lorsque l’onde rencontre un objet qui entrave une partie de sa propagation (typiquement le bord d'un mur ou le bord d'un objectif). Elle est ensuite diffractée avec d'autant plus d'intensité que la dimension de l'ouverture qu'elle franchit se rapproche de sa longueur d'onde : une onde type radio sera facilement diffractée par des bâtiments dans une ville, tandis que la diffraction lumineuse y sera imperceptible. Cette dernière commencera en revanche à se faire ressentir dans un objectif où elle imposera d'ailleurs une limite théorique de résolution.

Pour être mise en évidence clairement, la taille de l’élément diffractant que rencontre l’onde doit avoir une taille caractéristique relativement petite par rapport à la distance à laquelle l'observateur se place. Si l’observateur est proche de l'objet, il observera l’image géométrique de l’objet : celle qui nous apparaît habituellement. La diffraction des particules de matière, c’est-à-dire l'observation des particules de matière projetées contre un objet, permet de prouver que les particules se comportent aussi comme des ondes.

Plus la longueur d’une onde est grande par rapport à un obstacle, plus cette onde aura de facilité à contourner, à envelopper l’obstacle. Ainsi les grandes ondes (longueurs d'ondes hectométriques et kilométriques) peuvent pénétrer dans le moindre recoin de la surface terrestre tandis que les retransmissions de télévision par satellite ne sont possibles que si l’antenne de réception « voit » le satellite.

Concernant l’approche calculatoire, deux méthodes peuvent être utilisées. Premièrement, on peut considérer que chaque surface élémentaire de l’objet émet une onde sphérique proportionnelle à cette surface (principe de Huygens-Fresnel), et on somme (ou on intègre) la contribution de chaque surface. Deuxièmement, pour expliquer totalement la figure de diffraction, on utilise la théorie de Kirchhoff.

La notion d'interférence prend toute son ampleur lorsque l’objet a une structure périodique (réseau). Dans ce cas, l’objet peut être représenté comme une cellule élémentaire répétée à intervalles réguliers. Le résultat de l’onde est alors la superposition — l’interférence — des ondes diffractées par les différentes cellules (la cellule unitaire étant elle-même composée de points qui diffusent chacun l’onde). C’est ce phénomène qui cause l'irisation par un CD-ROM.

Dans l’approche du phénomène, on a donc deux niveaux d’interférence : la cellule unitaire (diffraction par une seule cellule), et entre les cellules (diffraction de l'objet complet).

Historique

D'un point de vue historique la diffraction a été découverte avec la lumière en 1665 par Grimaldi. Elle fut interprétée correctement comme un comportement ondulatoire par Huygens, puis étudiée par Fresnel et Fraunhofer suite aux expériences de Young (trous d'Young).

Pour des raisons historiques, on distingue encore la diffraction des interférences alors qu'il n'y a pas lieu de le faire : ces deux comportements dérivent de la nature ondulatoire d'un phénomène et ne vont pas l'un sans l'autre : Il n'y a pas de diffraction sans interférences.

La réciproque n'est pas vraie, il existe des interférences sans diffraction dans le cas des interférences par division d'amplitude : coin d'air, anneaux de Newton, Perot-Fabry…

Approche théorique

L'origine de la diffraction est la nature ondulatoire du phénomène et pour l'aborder il faut donc en théorie remonter à l'équation d'onde. On peut montrer qu'une bonne approximation de la solution d'un problème de diffraction est donnée par le principe de Huygens-Fresnel dans certaines conditions bien précises (approximation paraxiale, c'est-à-dire l'observation à relativement grande distance par rapport aux dimensions de l'obstacle). Ce principe est fondé sur l'idée qu'on peut considérer chaque point d'un front d'onde comme une source secondaire et que l'onde observée un peu plus loin est le résultat des interférences entre ces sources ponctuelles. Une telle vision des choses est rendue possible grâce à la linéarité de l'équation d'onde.

L'optique de Fourier est le domaine qui traite du comportement ondulatoire de la lumière à travers un système de lentilles et d'ouvertures dans l'approximation paraxiale. Pour simplifier les calculs, on utilise souvent la notion de produit de convolution.

Exemples de phénomènes de diffraction

Diffraction par un trou circulaire

Diffraction par un trou carré

Exemple typique en mécanique des fluides : vagues pénétrant dans un port en contournant une jetée.

Exemples typiques en acoustique :

trompes des alarmes allongées verticalement (permet la diffusion du son horizontalement) ;

les portes presque fermées laissent quand même passer un haut niveau sonore : diffraction par l’entrebâillement.

Exemples typiques en optique :

diffraction par un trou circulaire (tache d'Airy) ;

diffraction par une fente ;

diffraction par deux trous ou deux fentes (trous d'Young ou fentes de Young) ;

limitation de la taille des défauts visibles en microscopie optique

Réseau de diffraction optique ;

Limite de diffraction des instruments optiques.

Exemples typiques en cristallographie :

diffraction de rayons X (DRX) ;

diffraction de rayons gamma

diffraction de neutrons ;

diffraction d'électrons en microscopie électronique en transmission (MET) ;

lignes de Kikuchi en microscopie électronique à balayage (méthode EBSD) ;

spectrométrie par analyse dispersive en longueur d'onde (WDS wavelength dispersion spectrometry).

红色激光的圆孔衍射图样

绕射（英语：diffraction），又称衍射，是指波遇到障碍物时偏离原来直线传播的物理现象。

在古典物理学中，波在穿过狭缝、小孔或圆盘之类的障碍物后会发生不同程度的弯散传播。假设将一个障碍物置放在光源和观察屏之间，则会有光亮区域与阴晦区域出现于观察屏，而且这些区域的边界并不锐利，是一种明暗相间的复杂图样。这现象称为衍射，当波在其传播路径上遇到障碍物时，都有可能发生这种现象。除此之外，当光波穿过折射率不均匀的介质时，或当声波穿过声阻抗不均匀的介质时，也会发生类似的效应。在一定条件下，不仅水波、光波能够产生肉眼可见的衍射现象，其他类型的电磁波（例如X射线和无线电波等）也能够发生衍射。由于原子尺度的实际物体具有类似波的性质，它们也会表现出衍射现象，可以通过量子力学进行研究其性质。

在适当情况下，任何波都具有衍射的固有性质。然而，不同情况中波发生衍射的程度有所不同。如果障碍物具有多个密集分布的孔隙，就会造成较为复杂的衍射强度分布图样。这是因为波的不同部分以不同的路径传播到观察者的位置，发生波叠加而形成的现象。

衍射的形式论还可以用来描述有限波（量度为有限尺寸的波）在自由空间的传播情况。例如，激光束的发散性质、雷达天线的波束形状以及超声波传感器的视野范围都可以利用衍射方程来加以分析。

衍射与干涉的关系

美国物理学家、诺贝尔物理学奖得主理乍得·费曼指出： “ 没有人能够令人满意地定义干涉和衍射的区别。这只是术语用途的问题，其实二者在物理上并没有什幺特别的、重要的区别。 ” 他还提到，如果只有少数的波源（例如两个的时候），我们称这现象为“干涉”，例如我们称杨氏双缝实验实验中双缝所产生的两束光源产生了干涉现象。而当大量波源存在时，对应的过程被称作是“衍射”。在实际情况中，衍射和干涉往往是同时出现的。有文献这样总结：干涉是有限多个波束“相加”的结果，而衍射则是无限多个波束“积分”的结果。

研究历史

意大利物理学者弗朗西斯科·格里马第（1618-1663）。 光的衍射效应最早是由弗朗西斯科·格里马第（Francesco Grimaldi）于1665年发现并加以描述，他也是“衍射”一词的创始人。这个词源于拉丁语词汇diffringere，意为“成为碎片”，即波原来的传播方向被“打碎”、弯散至不同的方向。格里马第观察到的现象直到1665年才被发表，这时他已经去世。他提出 “光不仅会沿直线传播、折射和反射，还能够以第四种方式传播，即通过衍射的形式传播。”（"Propositio I. Lumen propagatur seu diffunditur non solum directe, refracte, ac reflexe, sed etiam alio quodam quarto modo, diffracte."） 英国科学家艾萨克·牛顿对这些现象进行了研究，他认为光线发生了弯曲，并认为光是由粒子构成。在19世纪以前，由于牛顿在学界的权威，光微粒说在很长一段时间占有主流位置。这样的情况直到19世纪几项理论和实验结果的发表，才得以改变。1803年，托马斯·杨进行了一项非常著名的实验，这项实验展示了两条紧密相邻的狭缝造成的干涉现象，后人称之为“双缝实验”。在这个实验中，一束光照射到具有紧挨的两条狭缝的遮光挡板上，当光穿过狭缝并照射到挡板后面的观察屏上，可以产生明暗相间的条纹。他把这归因于光束通过两条狭缝后衍射产生的干涉现象，并进一步推测光一定具有波动的性质。奥古斯丁·菲涅耳则对衍射做了更多权威的计算研究，他的结果分别于1815年和1818年被发表，他提到 “这样，我就展示了人们能够通过何种方式来构想光以球面波连续不断地传播出去……”（ "J'ai donc montré de quelle façon l'on peut concevoir que la lumière s'étend successivement par des ondes sphériques, ..."） 法国科学院曾经举办了一个关于衍射问题的有奖辩论会，菲涅耳赢得了这次辩论。作为反对光波动说的其中一位，西莫恩·德尼·泊松提出，如果菲涅耳声称的结论是正确的，那幺当光射向一个球的时候，将会在球后面阴影区域的中心找到亮斑。结果，评审委员会安排了上述实验，并发现了位于阴影区域中心的亮斑（它后来被称作泊松光斑）。这个发现极大地支持了菲涅耳的理论。他的研究为克里斯蒂安·惠更斯发展的光的波动理论提供了很大的支持。他与杨的理论共同反驳了牛顿关于光是粒子的理论。 在对衍射现象的探索过程中，人们也不断积累了对于衍射光栅的认识。17世纪，苏格兰数学家、天文学家詹姆斯·格雷戈里（James Gregory）在鸟的羽毛缝间观察到了阳光的衍射现象。他是第一个发衍射光栅原理的科学家。在1673年5月13日他写给约翰·科林斯（John Colins）的一封信中提到了此发现。；1786年，美国天文学家戴维·里滕豪斯用螺丝和细线第一次人工制成了衍射光栅，细线的密度达到每英寸100线，他用这个装置成功地看到了阳光的衍射。1821年，约瑟夫·夫琅禾费利用相似的装置（每厘米127线）证明了托马斯·杨关于衍射的公式（参见段落下方），并对衍射进行了许多重要研究。1867年，刘易斯·卢瑟福（Lewis Morris Rutherfurd）采用水轮机作为动力进行刻线、制作光栅。后来的亨利·奥古斯塔斯·罗兰 改良了光栅的刻划技术，并在1882年发明了在凹形球面镜上进行刻划的凹面光栅。其后的罗伯特·伍德（Robert William Wood）改进了光栅的刻划形状，从而提高了光栅的衍射效率。近代的阿尔伯特·迈克耳孙提出利用干涉伺服系统控制光栅的刻划过程，于1948年实现了这一想法。20世纪下半叶，由于激光、光刻胶等新技术的出现，光栅制造技术取得很大的进步，制造成本显着降低，制造周期也得以缩短。

日常生活中的实例

图示为温泉上方水蒸气中的光环现象。光环是一种光波被水气或尺寸不均匀的小水滴反向散射到其波源的光学现象，整个过程包含了衍射、反射和折射。 衍射效应在日常生活中并不罕见。许多有关光的衍射实例都可以用肉眼观察到。例如，在CD或DVD光盘的表面，均匀地紧密排列着一系列的光轨，这些光轨相当于衍射光栅的作用。如果以一定的角度观察它们，会看到光在盘面表现出类似彩虹的彩色图样。将上述现象的基本原理加以利用，很多产生有意思衍射图样的衍射光栅，都可以被制备出来。衍射也是信用卡等所采用的全息摄影的技术基础之一。地球的大气层是由微小粒子组成的，因此它也能够使空间光源（例如太阳或者月亮）的光在大气层发生衍射，从而形成光环。此外，当激光照射到粗糙的光学界面上时，也能够发生衍射现象，产生散斑。上述所有例子都是光具有波动性的结果。 衍射是一切波的固有属性。即使是宏观的海浪，在防波堤或其他障碍物附近也能够发生衍射。此外，声波在障碍物边缘发生衍射，也是人站在障碍物（例如墙壁、树木）后面仍然能够听到声音的原因之一。不过，衍射也为照相机、望远镜和显微镜等光学仪器的的分辨率设定了一定的限制。

物理机制

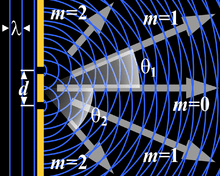
惠更斯原理的示意图：可以看出，狭缝处诸点光源作为次生光波的光源向各个方向发出光波。 光波（或其他波）传播的路径不同，可能造成衍射现象的发生。可以用惠更斯－菲涅耳原理和波的叠加原理对现象进行描述。这个理论认为，可以把波前的每一点考虑为次波（球面波）的点波源，这些次波就是后续时刻的波面。这个原理最早由惠更斯于17世纪提出，不过他并未虑及波的时空周期性（他认为光是一种非周期性的、无规则的脉冲）。1818年左右，菲涅耳在巴黎科学院关于解释衍射现象的有奖竞赛中，吸收了惠更斯“次波”的思想，并加入了他对于干涉现象的理解，使上述理论得以发展和完善。后人将这个理论称为“惠更斯－菲涅耳原理”。根据这一理论，任意后续位置的波位移等于这些次波求和。求和并非简单的代数和，而必须虑及这些波各自的相对相位以及振幅。因此，它们叠加之后的振幅范围介于0（相互完全抵消）和所有次波振幅的代数总和之间。我们可以通过光学实验，观察到光波的衍射图样。光的衍射图样通常具有一系列明暗条纹（分别对应光波振幅的最大值和最小值）。 人们为了分析波的衍射现象，构造了许多数学模型，其中包括从波动方程推导出的菲涅耳－基尔霍夫衍射公式、夫琅禾费衍射模型以及菲涅耳衍射模型。设为圆孔半径或狭缝宽度，为入射波的波长，为观察屏距离圆孔、狭缝等衍射物体的距离，如果它们满足 我们就称其为菲涅耳衍射，它是衍射的近场近似； 如果它们满足 我们就称其为夫琅禾费衍射，它是衍射的远场近似。 大多数情况，获得衍射方程的严格解析解较为困难，可以通过有限元分析和边界元分析方法来求得数值解。实际的衍射过程通常很复杂，不过，如果能够将实际情况简化到二维平面上，则对于衍射的数学描述将变得相对简单。例如，水波就可以近似地看做是分布在二维平面上的机械波。而对于光波，如果它遇到的衍射物体在某一个方向的尺度远大于光的波长，从而造成这个方向的衍射现象不显着，那幺，在分析计算时可以将其忽略，这样做并不会严重影响分析结果。例如，狭缝问题就可以简化到二维的情况，这是因为其沿着缝隙方向的长度和入射光波长相差甚远，因此我们只需考虑它宽度和厚度这两个方向。然而，当我们考虑入射光穿过圆孔时，则必须完整地考虑其三维方向光的传播细节。

光的衍射

为给定角度位置处的辐照度

初始辐照度

当时，，在原点处

i为光波入射到光栅的角度，如果是垂直入射到平面光栅，则

为光栅刻线的间距，也成为光栅常数

为非零整数

红色激光通过衍射光栅所产生的衍射。

红色激光的多缝衍射图样，上方所示的是2条狭缝的情况，下方为5条狭缝的情况。

波长为633纳米的激光通过一个具有150条狭缝的网格

衍射波的普遍性质

衍射波的角间距与造成衍射的物体的尺寸负相关。也就是说，造成衍射的物体的尺寸越小，它所形成的衍射条纹越宽，反之亦然。例如，在单缝衍射里，根据公式，当入射波的波长一定时，狭缝宽度越小，第一极小值对应的就越大，从而造成中间的亮纹宽度增加；

某一级衍射角的大小，只取决于入射波的波长与衍射物体尺寸的相对比值；

当造成衍射的物体结构具有周期性（例如衍射光栅），则衍射后的图样会变得更窄。例如，对比2条狭缝产生的衍射与5条狭缝产生的衍射，两种情况的狭缝间距相等，不过5条狭缝产生的衍射图样更细（参见衍射光栅一节的第三幅插图）。

粒子衍射

量子理论指出，所有的实物粒子都具有波动性。特别的，大质量粒子可以发生明显的干涉和衍射现象。电子和中子的衍射是量子力学的重要关注对象。根据德布罗意假设， 这里为普朗克常数，是实物粒子的动量（低速情况下等于质量和速度的乘积）。 对于大多数宏观粒子来说，它们所具有的德布罗意波长非常短，不足以表现明显的波动性。例如，以每秒30,000米移动的钠原子，其德布罗意波长大约为50皮米（pico meter）。德布罗意在进行论文答辩时让·佩兰曾询问他如何证明他所谓的“物质波”，德布罗意回答说：“用晶体对电子的衍射实验可以做到”。后来，电子在镍晶体的衍射印证了他的假设。 即便是最小的宏观物体，其波长还是非常小，因此物质波的衍射现象只能在微观的粒子（例如电子、中子、原子和小分子）上体现。这些物质的短波长使得它们很适合用来研究固体和大分子（诸如蛋白质）的原子晶体结构。 一些相对较大的分子，像富勒烯，也能表现出衍射现象。

布拉格衍射

为入射波（如常用的X射线等）波长

为晶面间距

为衍射角度

为衍射级数

光的相干性

同一波源发射的波，由于传播路径不同，会在观察屏上产生的干涉情况。采用这种描述，经过不同路径到达给定点的波之间的相位差只与它们的有效光程有关，而与时间无关。正因为如此，观察屏上给定点的明暗情况是确定的，这样总体上会形成稳定的图样。如果采用不相干入射光，那幺其中的不同波传播到给定点时的相位差将会极快地、无规则地变化，这样在观察屏上就无法形成稳定的干涉相长或干涉相消的图样，而是在这两种情况之间不断变化，以至于无法观察到明暗条纹。 一束光波的相位在某段长度上是相关的，这段长度被称作是相干长度。为了使干涉能够发生，光程差必须小于相干长度。有时候，这被称为波谱相干性，因为它与波中存在的不同频率成分有关。在原子跃迁发射光波的情况中，相干长度与原子产生跃迁的激发态的寿命有关。 如果光波由扩展光源发射，则可能会出现横向的不相干。当观察一束光的截面时，相位在某段横向距离上是相关的，这段横向距离被称作是「横向相干长度」（transverse coherence length）。在杨氏双缝实验中，这意味着如果横向相干长度比两条狭缝的间距小，那幺在观察屏上形成的图样看起来就像是两个独立单缝形成的衍射图样。 在电子、中子和原子等离子的情况中，相干长度与描述粒子的波函数的空间范围有关。