Vague se brisant sur la côte sauvage de l'île d'Yeu.
Des vagues sur l'Atlantique Nord - navire dans la tempête.
Une vague () est une déformation de la surface d'une masse d'eau le plus souvent sous l'effet du vent. À l'interface des deux fluides principaux de la Terre, l'agitation de l'atmosphère engendre sur les océans, mers et lacs, des mouvements de surface sous la forme de successions de vagues, de même allure mais différentes. Les séismes majeurs, éruptions volcaniques ou chutes de météorites créent également des vagues appelées tsunamis ou raz-de-marée. La marée est également à l'origine de vagues très particulières, appelés mascarets, qui se produisent dans les circonstances où l'onde de marée rencontre un courant opposé et de vitesse égale. Certains phénomènes météorologiques peuvent être à l'origine de « météo-tsunamis » (ou tsunamis météorologiques, dont la vague peut avoir les mêmes caractéristiques que celle d'un tsunami)
Les trains de vagues provoqués par le vent se propagent en se dispersant, les vagues les plus cambrées peuvent déferler en créant des turbulences et des courants marins. Il s'agit d'ondes de gravité, la force de rappel étant la pesanteur : leur évolution est déterminée par les propriétés communes aux ondes comme la réflexion, la réfraction et la diffraction.
La hauteur des vagues varie de quelques centimètres à 32,3 m pour la plus haute enregistrée par un instrument, voire plus de 34 m pour la plus haute vague observée visuellement et 36 m de maximum extrapolés d'une moyenne de 20,1 m lors de la tempête Quirin en février 2011.
La tendance à parler de houle pour désigner tous les types de vague, vagues régulières et vagues irrégulières, est un abus de langage.
La description la plus élémentaire de ce phénomène compliqué repose sur la notion de hauteur significative d'un état de mer. Lorsque la hauteur d'une vague individuelle dépasse exceptionnellement le double de cette hauteur on parle de « vague scélérate » susceptible de causer des dommages importants aux navires du fait de l'effet de surprise. Les calculs ou les études sur modèles réduits relatifs aux vagues sont fréquemment simplifiés en considérant une vague régulière (périodique) dont la hauteur est le plus souvent égale à la hauteur significative de l'état de mer considéré. Pour des problèmes plus particuliers on raisonne sur la hauteur maximale. Enfin le comportement dynamique d'un navire ou d'un autre corps flottant est étudié en utilisant la notion plus précise de vague irrégulière.
Représentations mathématiques
L'astronome et mathématicien George Biddell Airy a fourni la théorie la plus simple pour des vagues régulières (périodiques). L'onde d'Airy possède une surface libre de forme sinusoïdale. Il s'agit d'une représentation très simplifiée de la réalité, valable en principe pour des vagues régulières de faible cambrure. La cambrure est définie comme le rapport de la hauteur sur la longueur d'onde. Cette théorie est néanmoins efficace pour résoudre de nombreux problèmes pratiques, à condition de savoir associer des caractéristiques pertinentes au phénomène naturel beaucoup plus compliqué qui sera évoqué ci-dessous.
Si on regarde avec attention les vagues en mer, on constate que la plupart d'entre elles ne sont pas sinusoïdales : les crêtes sont plus pointues, les creux plus aplatis. Cet aspect est pris en compte en remplaçant l'approximation d'Airy, au premier ordre, par des approximations périodiques d'ordre supérieur généralement attribuées à Stokes.
Estampe japonaise, extraite des trente-six vues du Fuji de Katsushika Hokusai
En observant la succession des vagues, on s'aperçoit qu'elles ne présentent aucune régularité : il n'y a jamais deux vagues identiques. On est ainsi amené à décrire l'état de la mer de manière statistique. Un modèle simple repose sur l'analyse spectrale qui décompose la surface de la mer en une somme d'une infinité d'ondes infiniment petites ayant la même direction. Cette description basée sur une simple sommation de vagues d'Airy ne prend pas en compte les non-linéarités introduites par Georges Stokes, imperfection dont on se satisfait très généralement.
Pour des profondeurs beaucoup plus petites que la longueur d'onde et pour certaines applications en grande profondeur, en particulier pour la mer du vent, la superposition d'ondes d'Airy n'est plus assez précise. On peut alors utiliser différentes techniques comme la transformation de Creamer, ou les modèles spectraux d'ordre supérieur. La seule difficulté qui ne soit pas encore résolue est la représentation fidèle du déferlement.
Sans avoir recours à ces modèles plus complexes, il est souvent utile de se ramener à une vague linéaire et périodique de même énergie. En effet, pour des vagues linéaires, les propriétés quadratiques que sont l'énergie ou la dérive de Stokes s'additionnent. On peut ainsi déduire l'essentiel des propriétés (hauteur, vitesse des particules, pression…) associées aux vagues irrégulières par la racine de la somme des carrés de ces mêmes propriétés pour des vagues régulières.
Propagation des vagues
Comme toutes les ondes, en particulier les ondes lumineuses décrites par l'optique, les vagues peuvent se réfléchir, se diffracter et se réfracter. Ces phénomènes, faciles à caractériser pour des vagues régulières, se compliquent pour les vagues naturelles tout en restant qualitativement analogues. À la différence des phénomènes lumineux, les vagues ont des longueurs d'onde à notre échelle, ce qui facilite la compréhension.
Réflexion
Mer gaufrée. Pointe des Baleines, île de Ré, France
La réflexion se produit sur un ouvrage de hauteur immergée importante par rapport à la profondeur et de largeur importante par rapport à la longueur d'onde.
Lorsque des vagues arrivent parallèlement à une digue verticale il se produit une réflexion totale, phénomène d'onde stationnaire. Sur la paroi et à des distances proportionnelles à la demi-longueur d'onde on observe des ventres où l'amplitude est le double de l'amplitude incidente. Entre deux ventres successifs il y a un nœud où l'agitation semble disparaître.
Devant une digue à talus se produit une réflexion partielle avec des ventres dont l'amplitude est inférieure au double de l'amplitude incidente tandis que les nœuds n'ont plus une amplitude nulle.
Si les vagues arrivent obliquement la superposition de ondes incidentes et réfléchies produit une mer gaufrée.
Diffraction
Les phénomènes se compliquent au voisinage d'un obstacle de dimensions relativement petites vis-à-vis des longueurs d'onde, comme un navire, ou de l'extrémité d'une jetée.
Face à un obstacle, l'approximation de l'optique géométrique décrit le comportement de la lumière aux échelles supérieures aux longueurs d'onde, ce qui fait apparaître une zone d'ombre derrière l'obstacle. Les obstacles rencontrés par les vagues ayant toujours des dimensions de l'ordre des longueurs d'onde, il faut faire appel à la notion de diffraction selon laquelle il se produit toujours une agitation dans l'ombre géométrique.
Réfraction
La diminution de la célérité avec la profondeur conduit à des phénomènes de réfraction qui s'interprètent simplement en remarquant que la longueur d'onde varie proportionnellement à la célérité. Un élément de crête arrivant obliquement par rapport aux isobathes (lignes d'égale profondeur) possède une extrémité qui se trouve sur une profondeur inférieure à celle de l'autre extrémité. Les longueurs d'onde étant différentes la crête bascule de manière à se rapprocher de la direction de l'isobathe. De manière imagée on dit que les hauts fonds freinent les vagues.
Sur une plage, les crêtes se rapprochent donc de la ligne de rivage jusqu'à ce que la profondeur soit assez faible pour que s'amorce le déferlement. Sur une pointe il y a concentration des orthogonales (analogues aux rayons lumineux), donc augmentation de l'agitation et une atténuation liée à l'épanouissement dans une baie. Le contournement d'un îlot peut créer dans l'« ombre géométrique » une augmentation de l'agitation par superposition des vagues provenant des deux côtés.
Les courants modifient aussi la vitesse de phase et la relation de dispersion. Ils induisent donc aussi une réfraction.
Vagues régulières et vagues irrégulières
La notion de vague régulière permet de résoudre un certain nombre de problèmes bien qu'elle soit assez éloignée de la réalité physique. En effet, le vent soufflant sur la surface de la mer crée une agitation erratique : c'est la mer du vent. Au cours de la propagation, la dispersion des vagues hors de la région de génération fait que celles-ci prennent une apparence de plus en plus régulière : c'est la houle. La houle naturelle se rapproche des vagues régulières sans jamais y arriver car elle perd des composantes sans jamais devenir un phénomène monochromatique.
L'état de la mer, combinaison de la houle et de la mer de vent, présente souvent sous la forme de mers croisées, la direction du vent local étant rarement la même que celle de la houle.
Une fois posées des hypothèses classiques de la mécanique des fluides, le problème de la description des vagues régulières se réduit à la recherche d'approximations adaptées à telles ou telles circonstances particulières. Au contraire, avant de penser à une description mathématique des vagues de la nature il a fallu élaborer des techniques d'acquisition et de traitement des données.
Vagues régulières en profondeur constante
Problème
Domaine de validité des théories approchées pour les vagues régulières, en fonction de la profondeur h, hauteur de la vague H, période temporelle de la vague τ et pesanteur g.
Une vague périodique est caractérisée par
la profondeur ,
la hauteur de crête à creux ou l'amplitude qui est la moitié de celle-ci,
et la longueur d'onde ou le nombre d'onde .
En nombres sans dimension elle est caractérisée par
la cambrure ou le produit
et la profondeur relative ou le produit .
Cette description correspond à une modélisation grossière qui ignore les irrégularités des vagues de la nature et leur aspect tridimensionnel. Elle suppose également une profondeur constante bien qu'elle en fournisse en de nombreuses circonstances une approximation raisonnable.
Elle relève du problème le plus simple de la mécanique des fluides qui ignore la viscosité, la compressibilité, l'existence de tourbillons (écoulement irrotationnel d'un fluide incompressible et parfait). Dans ces conditions la description eulérienne classique du champ des vitesses se réduit à la recherche d'un potentiel harmonique. Le caractère non-linéaire de la condition à la surface libre interdit néanmoins la recherche de solutions simples rencontrées dans d'autres problèmes physiques.
Trois types d'approximations sont utilisés.
Les approximations de Stokes conviennent pour des profondeurs relativement importantes par rapport à la longueur d'onde. Elles satisfont exactement l'équation de Laplace et la condition au fond.
Les approximations cnoïdales adaptées à des profondeurs plus faibles ne satisfont pas l'équation de Laplace.
Les approximations utilisant la fonction de courant sont formellement identiques aux approximations de Stokes mais obtenues par une méthode de moindres carrés au lieu d'un développement limité. Le calcul numérique permet de satisfaire presque exactement la condition dynamique (l'erreur tolérée peut être aussi petite que souhaitée) et exactement toutes autres les conditions, quelle que soit la profondeur.
Le diagramme décrit dans un plan (profondeur relative/cambrure) le domaine de validité de différentes approximations borné par la cambrure limite au-delà de laquelle la vague déferle. Plus précisément la profondeur et la hauteur sont rapportées à la longueur d'onde en profondeur infinie multipliée par 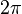 .
.
Approximations de Stokes
Une solution naturelle consiste à exprimer le potentiel et, par suite, les différentes grandeurs par des développements limités en fonction du paramètre , c'est-à-dire de la cambrure supposé petite.
En ne retenant que le premier terme du développement on obtient un modèle linéaire pour les champs de vitesse et pression, connu sous le nom de vague d'Airy, qui n'est donc valable en principe que pour les vagues de cambrure infiniment petite, tous les termes supprimés étant alors des infiniment petits d'ordres supérieurs, donc négligeables. Il présente deux caractéristiques :
La surface libre est sinusoïdale.
Les trajectoires des particules fluides sont elliptiques.
Pour des raisons de simplicité, la vague d'Airy est souvent utilisée au-delà de son domaine de validité théorique. Son caractère linéaire permet de superposer les solutions, et de constituer ainsi un état de mer assez réaliste sous la forme d'une somme de vagues de différentes périodes et directions.
Dès que la cambrure n'est pas très petite il peut être préférable, au prix de calculs plus laborieux, d'utiliser des modèles de vagues d'amplitude finie obtenus en ajoutant des corrections d'ordres supérieurs. Ils améliorent le réalisme en ce qui concerne les deux points précédents.
À mesure que les ordres d'approximation s'élèvent la surface libre présente de crêtes de plus en plus pointues et des creux de plus en plus aplatis. L'approximation du cinquième ordre est généralement jugée assez réaliste pour la description des vagues régulières, sauf quand la vague s'approche de la cambrure maximale.
Un terme de dérive proportionnel au carré de l'amplitude déforme les trajectoires elliptiques du premier ordre pour donner naissance à des trajectoires qui ressemblent vaguement à des cycloïdes allongées. Une méthode élégante () permet de déterminer cette dérive en corrigeant le champ de vitesses d'Euler par un calcul dans les coordonnées de Lagrange. Néanmoins la cohérence du développement limité exige que cette correction soit considérée comme un terme du deuxième ordre négligeable au premier ordre (pour une description élémentaire du mécanisme général de dérive, voir Dérive d'un navire amarré).
Approximations en eau peu profonde

mouvement et dérive des particules en faible profondeur
Le développement limité de Stokes perd de sa signification lorsque la profondeur relative devient inférieure à 1/8 environ. Dans ces conditions on observe des crêtes très pointues séparées par des creux très étendus. Ce phénomène est pris en compte par le modèle de la vague cnoïdale qui tend vers deux limites :
La vague sinusoïdale d'Airy lorsque la hauteur est petite par rapport à la profondeur.
L'onde solitaire lorsque la longueur d'onde est grande par rapport à la profondeur. L'onde qui se situe alors entièrement au-dessus du niveau de repos ne présente plus de périodicité.
Approximations de la fonction de courant
Le modèle cnoïdal n'est cependant pas adapté aux vagues de fortes cambrures.
La méthode utilisée est un peu analogue à celle des approximations de Stokes avec deux différences. La fonction de courant remplace le potentiel et il ne s'agit plus d'un développement limité classique qui néglige les termes d'ordres supérieurs. Une fois choisi le degré de l'approximation, les coefficients sont déterminés en minimisant l'erreur au sens de la méthode des moindres carrés.
Cette méthode développée par Dean puis Dalrymple (1974) peut fournir des approximations meilleures que celles qui précèdent. On peut ainsi retrouver la forme de la vague de cambrure maximale, qui présente une crête pointue formant un angle de 120°.
Instabilité des vagues périodiques
En pratique les vagues ne sont jamais exactement périodiques, même en laboratoire, car les solutions mathématiques périodiques sont instables : les vagues évoluent vers d'autres formes, avec des trains de vagues irréguliers (instabilité modulationnelle de Benjamin et Feir) ou vers le déferlement (instabilité de la crête, mise en évidence par Tanaka). De nombreuses autres instabilités existent qui peuvent créer spontanément des formes en trois dimensions (vagues en fer à cheval par exemple).
Propagation des vagues (modèle d'Airy)
La première approximation de Stokes, à l'ordre 1 en fonction de ka, donne la théorie linéaire des vagues, aussi appelée modèle d'Airy. Elle est particulièrement bien adaptée pour décrire les houles de faible cambrure, pour des profondeurs grandes par rapport à l'amplitude des vagues.
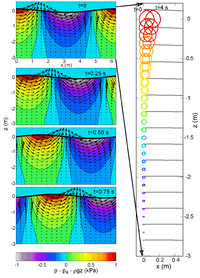
Onde d'Airy d'une période de 2 secondes par 3 mètres de fond. À gauche : vitesses et variations de pression, à droite trajectoire de particules pendant 4 secondes.
Relation de dispersion
Le mouvement des vagues peut être considéré comme irrotationnel, il dérive donc d'un potentiel. Comme l'eau est pratiquement incompressible, ce potentiel satisfait l'équation de Laplace. Pour les longueurs d'onde supérieures à 30 cm, la tension superficielle peut être négligée, et les solutions périodiques de faible amplitude (ondes d'Airy) obéissent à une relation de dispersion :
-
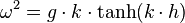 ,
,
avec
la pulsation de l'onde,
la période de la houle,
l'intensité de la pesanteur,
le nombre d'onde,
la longueur d'onde de la houle,
la profondeur de l'eau.
Cette relation donne la célérité de propagation de l'onde :
-

Pour des vagues régulières, cette relation est correcte à 10 % près en eau profonde, et l'erreur peut atteindre 30 % en eau peu profonde. En effet la célérité augmente aussi avec l'amplitude des vagues.
On constate que la vitesse des vagues augmente avec la période : les vagues se dispersent, sauf dans la limite des faibles profondeurs. Ainsi les trains de vagues les plus longs générés par une tempête arrivent avant les vagues plus courtes. Pour les grandes profondeurs (au-delà de la moitié de la longueur d'onde), la vitesse des vagues ne dépend plus de la profondeur puisque la tangente hyperbolique tend vers 1.
La relation de dispersion permet aussi de comprendre le comportement des vagues à l'approche du littoral. Quand la profondeur diminue spatialement, la période reste constante. Les formules ci-dessus entraînent l'augmentation du nombre d'onde, donc la diminution de la longueur d'onde et de la célérité.
Pour simplifier, dans le cas de l'eau profonde :
célérité (vitesse de propagation ou vitesse de phase) en m/s : ;
période (temps qui sépare deux crêtes) : ;
longueur d'onde : .
Vitesse de groupe
La vitesse de groupe , vitesse du transport d'énergie varie de façon plus complexe. En partant de l'eau profonde augmente de 20 % environ avant de décroître elle aussi. Par grands fonds . Ainsi les vagues vont plus vite que les groupes : elle prennent naissance à l'arrière du groupe, le dépassent et meurent à l'avant du groupe. Par petits fonds , et les vagues ne sont plus dispersives.
Énergie et vitesse de dérive
La quantité d'énergie mécanique par unité de surface de la mer (on parle de densité spatiale de l'énergie) est, en moyenne sur la période des vagues, égale à , dans le cas des vagues d'Airy. Cette densité s'exprime en joules par mètre carré, et c'est la somme des énergie potentielle et énergie cinétique. Lorsque les vagues se propagent frontalement vers la côte, le flux d'énergie par unité de longueur de crête est . Sans dissipation d'énergie et sans courants, ce flux est constant. Des vagues qui se propagent vers la côte voient donc leur hauteur diminuer de 10 % environ avant d'augmenter jusqu'à ce qu'elle finissent par déferler, lorsque la vitesse des particules d'eau atteint la vitesse de phase de la vague qui les supporte.
Les vagues sont aussi associées à une dérive. Sur l'ensemble de la colonne d'eau cette dérive donne un débit de masse égal à , qui s'exprime en kilogrammes par mètre. Ce débit est la quantité de mouvement du champ de vagues. La mise en place de ce débit, lors de la propagation, nécessite un flux de quantité de mouvement: ainsi les vagues transportent la quantité de mouvement depuis la région où le vent les a généré, jusqu'aux côtes où cette quantité de mouvement est transmise au courant littoral.

Une vague formée par un ferry
Mouvement du fluide
Dans la théorie d'Airy, les particules de fluide décrivent des ellipses presque fermées, dont la taille décroît avec la profondeur. En eau profonde (profondeur supérieure à la moitié de la longueur d'onde) ces ellipses sont des cercles.
Le fait que les ellipses ne soient pas tout à fait fermées est une manifestation de la dérive de Stokes. Près de la surface libre, la vitesse d'une particule d'eau est plus importante sous une crête que la vitesse opposée lors du passage du creux suivant. Il en résulte une dérive dans le sens de propagation des vagues qui peut s'inverser en profondeur. Pour les vagues générées par le vent, cette dérive est d'environ 1,5 % de la vitesse du vent pour un état de mer complètement développé et en eau profonde.
Validité et limitations
Pour une vague prise individuellement, l'approximation d'Airy est particulièrement bien vérifiée dans le cas de la houle constituée par des vagues peu cambrées se propageant au large et soumises à peu de vent. À mesure que la cambrure augmente, elle devient de plus en plus imprécise mais est néanmoins souvent utilisée à cause de sa simplicité. Pour certains problèmes qui demandent une grande précision, l'amplitude des ondes peut nécessiter approximation supérieure est utilisée.
L'approximation d'Airy, devient très imparfaite dans les faibles profondeurs et doit être remplacée par exemple par l'approximation cnoïdale. Elle est également imparfaite dans une zone de déferlements, que ce soit dans la zone de génération de la mer du vent ou sur des hauts fonds.
Enfin, pour des états de mer réels (irréguliers), on peut obtenir les caractéristiques des vagues en superposant un grand nombre de houles d'Airy. Là aussi, on peut être amené à utiliser des corrections non-linéaires pour retrouver des creux plus plats que les crêtes (correction de Creamer par exemple).
Déferlement
Dans l'ensemble des vagues générées par le vent, ou dans les trains de houle se propageant par petits fonds ou contre des courants adverses, certaines vagues sont trop cambrées pour être stables : elles déferlent.
À l'approche d'un rivage, à mesure que la profondeur diminue, la forme des vagues se modifie, d'abord à peu près symétriquement puis en général avec une face avant de plus en plus raide jusqu'à l'instabilité qui se produit lorsque la hauteur de la vague est du même ordre que la profondeur. Quand la vague se brise, l'essentiel de son énergie est dissipée en tourbillons et formation de bulles d'air. La quantité de mouvement qui était associée à la vague contribue à accélérer le courant dans la direction du déferlement.
La forme d'un déferlement au voisinage du rivage dépend essentiellement de la pente des fonds. En allant dans le sens des pentes croissantes on distingue le plus souvent trois types de déferlement. Le déferlement progressif ou glissant (spilling breaker en anglais) se produit généralement sur les plages à très faible pente. Les vagues commencent à se briser loin du rivage avec une crête à l'aspect mousseux qui s'accentue lors de la progression en laissant derrière une couche d'écume.
Le déferlement plongeant (plunging breaker en anglais) est particulièrement spectaculaire avec ses rouleaux appréciés par les surfers. La vague s'enroule autour d'une poche d'air puis s'écroule en créant une éclaboussure notable. Cela tend à se produire le plus souvent sur une forte pente ou sur un changement brutal de la profondeur (un rebord rocheux ou un écueil). Il y a beaucoup plus d'énergie dissipée que d'énergie réfléchie sur la plage.
Le déferlement frontal ou gonflant (surging breaker en anglais) se forme comme le déferlement plongeant mais la vague gravit la plage avant que la crête puisse s'enrouler. La zone de déferlement est très étroite et une grande partie de l'énergie est réfléchie vers les plus grandes profondeurs.
Certains considèrent aussi un cas intermédiaire entre les déferlements plongeant et gonflant (collapsing breaker). Au lieu de constituer un rouleau, la vague présente une face verticale avant de s'effondrer.
Vagues irrégulières
Description statistique
Observations visuelles
Les premières données chiffrées sur l'agitation en mer ont été le résultat d'observations visuelles. L'observateur annonçait au bout de quelques minutes une hauteur de vagues, appelée hauteur significative, et, plus rarement, une période moyenne.
Ces observations ont d'abord été effectuées pour bâtir des statistiques relatives à des sites donnés. Elles ont ensuite été systématisées sur des navires, les résultats étant alors regroupés par zones géographiques.
Enregistrements analogiques
La mise au point de houlographes associés à des enregistreurs sur papier a montré l'évolution de la surface libre au cours d'un enregistrement. Ceci a permis d'élaborer un histogramme des hauteurs de vagues. Il s'est alors avéré que la moyenne du tiers des hauteurs les plus fortes était proche de la hauteur significative annoncée par un observateur entraîné, ce qui constitue une définition plus rationnelle.
Enregistrements numériques
L'informatique a été à l'origine de progrès spectaculaires grâce à l'utilisation d'enregistrements échantillonnés.
Le calcul de l'écart type des échantillons, appelé moyenne quadratique en matière de signaux, montre qu'il est proche du quart de la hauteur significative définie précédemment, ce qui conduit à une nouvelle définition dénuée d'ambiguïté.
L'histogramme des échantillons ressemble plus ou moins à un histogramme normal ou histogramme de Gauss. C'est conforme au théorème central limite car il s'agit de la somme d'un grand nombre de termes plus ou moins indépendants. C'est particulièrement bien vérifié avec une houle peu cambrée. Dans la mer du vent les vagues cambrées présentent une dissymétrie des crêtes et des creux analogue à celle qui a été évoquée à propos des vagues régulières. Comme dans de nombreux domaines cette distorsion est négligée compte tenu de l'efficacité de la loi de Gauss.
Description spectrale
Méthodes
L'analyse spectrale regroupe diverses méthodes de représentation d'un signal par une somme de sinusoïdes.
Le développement en série de Fourier représente un signal périodique par une somme de sinusoïdes d'amplitudes finies dont les fréquences sont les multiples de l'inverse de la période. Les descriptions de Stokes des vagues régulières sont constituées par les premiers termes de tels développements.
La transformation de Fourier permet de décrire un signal transitoire. L'idée consiste à effectuer un développement en série de Fourier d'un morceau quelconque du signal dont on fait tendre la longueur vers l'infini. Les fréquences des composantes se rapprochent indéfiniment tandis que leurs amplitudes tendent vers zéro. En multipliant par la longueur d'analyse on obtient pour chaque fréquence un résultat fini appelé densité d'amplitude. Bien qu'il s'agisse de notions physiques sans rapports, le couple amplitude/densité d'amplitude est formellement de même nature que le couple charge concentrée/charge répartie de la flexion (matériau).
Cette dernière technique est en principe applicable à l'enregistrement d'une tempête en mer qui possède un début et une fin assez bien identifiés. Malheureusement l'information obtenue à la suite de calculs importants est difficile à interpréter. Il est préférable d'utiliser une méthode un peu plus abstraite, également rencontrée en vibrations, qui fournit à moindre frais des informations plus utilisables.
Cas des vagues
L'idée consiste à remplacer le très long enregistrement par une séquence d'enregistrements disjoints, par exemple d'une vingtaine de minutes toutes les trois heures.
La succession d'enregistrements donne une idée raisonnable sur l'évolution de la tempête (ou de tout autre état de mer) tandis que chacun d'eux est supposé assez long pour fournir une information statistiquement significative mais assez court pour que le niveau d'agitation n'ait pas trop évolué. L'enregistrement est ainsi considéré comme une partie d'un signal qui n'évolue pas au cours d'un temps infini. Ces considérations assez floues sont précisées par la notion de processus stationnaire.
De toute façon, la seule information certaine sur le phénomène réside dans l'enregistrement. Elle peut être traduite dans le domaine des fréquences en utilisant la transformée de Fourier de l'enregistrement complété par des zéros aux époques où le phénomène n'a pas été enregistré. Si on a des raisons de croire que le signal était effectivement nul en dehors de l'enregistrement la transformation de Fourier le traduit parfaitement. S'il est du type transitoire avec de l'information perdue la densité d'amplitude en donne la meilleure approximation. Dans le cas des vagues cette approximation n'a plus aucun sens mais une analyse plus approfondie montre que la représentation correcte utilise la densité spectrale qui se déduit de la densité d'amplitude.
L'erreur attachée à la perte de l'information située hors de l'enregistrement se traduit par un filtre qui réorganise en fonction de la fréquence aussi bien la densité spectrale que la densité d'amplitude. Dans le cas des vagues s'ajoute une incertitude liée au fait que deux enregistrements de même longueur effectués à des époques différentes ne donnent pas exactement le même résultat.
Utilité de la densité spectrale
Lorsqu'une vague excite un système mécanique linéaire (par exemple un navire) la densité spectrale de sa réponse (par exemple le tangage du navire) se déduit de la densité spectrale de l'excitation par l'intermédiaire de la fonction de transfert du système.
Si l'excitation est considérée comme une réalisation d'un processus de Gauss la réponse du système linéaire possède la même propriété. Dans ces conditions la densité spectrale permet d'estimer la distribution des amplitudes de crêtes, la période moyenne de passage au zéro, la période moyenne de crête, etc.
Généralisation
La densité spectrale suffit pour décrire une houle épurée par son trajet qui possède des crêtes quasi-rectilignes. Dans la zone de génération on observe des vagues à courtes crêtes. Celles-ci peuvent être décrites comme des sommes de vagues sinusoïdales qui diffèrent non seulement par leurs fréquences mais aussi par leurs directions, ce qui conduit à la notion de densité spectro-angulaire.
Force des vagues et ressac
L'ingénieur écossais Thomas Stevenson met au point en 1843 un dynamomètre enregistreur spécial pour mesurer la force des vagues sur une surface verticale. Il met ainsi en évidence que la pression de l’eau sur les falaises, qui varie avec le type de vague et la profondeur, peut atteindre 30 tonnes / m dans les coups de vent d'hiver.
Le ressac est le retour violent des vagues sur elles-mêmes lorsqu'elles se brisent contre un obstacle. Il exerce un effet de succion, agissant sur le transport, l’ablation marine et le dépôt des sédiments.
La vague dans la culture
La vague par Guillaume Seignac (vers 1908).

La vague par William Thomas Horton, 1898.
La vague a inspiré diverses œuvres :
ci-contre : La Vague de Guillaume Seignac ;
ci-dessus : La Grande Vague de Kanagawa de Hokusai.
Les Jeux de l'Océan contre les falaises de Vendée du compositeur Emile Goué
The wave du peintre anglais symboliste ami de William Butler Yeats, William Thomas Horton, A book of images, 1898.
Galerie
Petites vagues un soir à Ajaccio, Corse.

 词典释义:
词典释义:
 ; 波浪形
; 波浪形 断的移民潮
断的移民潮

 ]
]

 , 含混,
, 含混,  明确
明确 其词
其词
 的, 含混的,
的, 含混的,  明确的
明确的


 的, 隐隐约约的
的, 隐隐约约的 的身
的身
 的回忆
的回忆 在焉的
在焉的 无关紧要的
无关紧要的

 )
) 定的
定的 界出现的)新浪潮派
界出现的)新浪潮派 的, 模
的, 模 的vaguef波, 波浪; 浪潮; 浪; 电波; 林窗vaguem迷走神经
的vaguef波, 波浪; 浪潮; 浪; 电波; 林窗vaguem迷走神经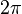 .
.

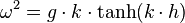 ,
,




