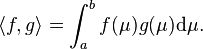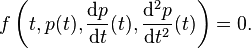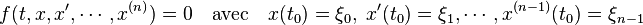Robert Recorde est un précurseur pour l'écriture d'une équation. Il invente l'usage du signe = pour désigner une égalité.
Un système dynamique correspond à un type particulier d'équation, dont les solutions recherchées sont des fonctions. Le comportement limite est parfois complexe. Dans certain cas, il est caractérisé par une curieuse figure géométrique, appelée attracteur étrange.
Une équation est, en mathématiques, une égalité contenant une ou plusieurs variables. Résoudre l'équation consiste à déterminer les valeurs que peut prendre la variable pour rendre l'égalité vraie. La variable est aussi appelée inconnue et les valeurs pour lesquelles l'égalité est vérifiée solutions. À la différence d'une identité, une équation est une égalité qui n'est pas nécessairement vraie pour toutes les valeurs possibles que peut prendre la variable.
Les équations peuvent être de natures diverses, on les trouve dans des branches différentes des mathématiques ; les techniques associées à leur traitement diffèrent selon leur type.
L'algèbre étudie surtout deux familles d'équations : les équations polynomiales et parmi elles les équations linéaires. Les équations polynomiales sont de la forme P(X) = 0, où P est un polynôme. Des méthodes de transformation et de changement de variable permettent de venir à bout des plus simples. Les équations linéaires sont de la forme a(x) + b = 0, où a est une application linéaire et b un vecteur. On utilise pour les résoudre des techniques algorithmiques ou géométriques, issues de l'algèbre linéaire ou de l'analyse. Modifier le domaine de définition de la variable peut changer considérablement la nature de l'équation. L'algèbre étudie également les équations diophantiennes, équations dont les coefficients et les solutions sont des entiers. Les techniques utilisées sont différentes et essentiellement issues de l'arithmétique. Ces équations sont en général difficiles, on cherche souvent uniquement à déterminer l'existence ou l'absence de solution et, si elles existent, leur nombre.
La géométrie utilise les équations pour caractériser des figures. L'objectif est encore différent des cas précédents, l'équation est utilisée pour mettre en évidence des propriétés géométriques. Il existe, dans ce contexte, deux grandes familles d'équations, les cartésiennes et les paramétriques.
L'analyse étudie des équations du type f(x) = 0, où f est une fonction ayant certaines propriétés comme la continuité, la dérivabilité ou encore le fait d'être contractante. Des techniques permettent de construire des suites convergeant vers une solution de l'équation. L'objectif est de pouvoir approcher la solution aussi précisément que possible.
Un système dynamique est défini par une équation dont les solutions sont, soit des suites, soit des fonctions d'une ou plusieurs variables. Il existe deux questions centrales : l'état initial et le comportement asymptotique. Pour chaque état initial admissible, par exemple la valeur de la suite ou de la fonction en zéro, l'équation admet une unique solution. Parfois, une petite modification de l'état initial modifie peu la solution. Ce n'est pas toujours le cas, cette sensibilité à la condition initiale est l'objet de la première question. Le comportement limite ou encore asymptotique d'une solution correspond à la forme de la solution quand la variable tend vers l'infini, ce comportement est l'objet de la deuxième question. S'il ne diverge pas, il peut, soit tendre vers une valeur donnée, soit s'approcher d'un comportement cyclique (une fonction périodique ou une suite parcourant toujours un même ensemble fini de valeurs et dans le même ordre), soit avoir un comportement chaotique, semblant évoluer au gré du hasard, même si la solution est par définition déterministe.
Remarque : Le terme inéquation correspond à une définition différente. Si dans certains cas particuliers les sujets sont connexes, dans le cas général ils sont suffisamment éloignés pour mériter des traitements distincts. L'inéquation est en conséquence traitée dans un article séparé.
Préambule
Définitions : équation, inconnue et solution
L'exemple suivant est extrait du livre d'Al-Khawarizmi, l'un des fondateurs de l'algèbre. « Un homme meurt et laisse quatre fils et il fait, à un homme, une donation égale à la part d'un de ses fils et, à un autre, le quart de la différence entre le tiers de l'héritage et la première donation. ». Si x désigne l'inconnue, ici la fraction de l'héritage que reçoit un fils, la question se traduit par l'équation suivante, où la valeur 1 à droite désigne 1 héritage :
Dans l'exemple, la formulation sous forme d'équation, c'est-à-dire l'égalité (1), est équivalente à la question posée. Y répondre revient à déterminer l'unique valeur que doit prendre l'inconnue x pour que l'égalité définissant l'équation soit vraie. Le maniement de l'inconnue permet de résoudre quelques équations, comme celle présentée ici. Cette vision est source d'une autre manière de définir une équation. Pour l'Encyclopédie Soviétique de Mathématiques, une équation est la traduction, sous une forme analytique, d'un problème. L'équation f(x) = g(x) correspond à la question : pour quelle valeur de x, l'équation se transforme-t-elle en égalité ? Cette définition décrit bien les premières équations étudiées, qui sont parfois la formulation mathématique d'une question de la vie courante.
Cette définition fondée sur une question n'est pas la plus générale : en géométrie, l'équation du cercle ne fait pas référence à une question. Cependant, la forme reste la même : une égalité entre deux expressions, utilisant deux variables généralement notées x et y.
Paramètre
Au XVI siècle, Viète, un mathématicien français, trouve une méthode pour exprimer de manière générique une famille d'équations. Pour en comprendre l'intérêt, illustrons le par une question.
Exemple d'équation paramétrée. Le graphe de la fonction f est la parabole illustrée en bleu sur la figure, celui de g1(x) la droite illustrée en rouge, celui de g-2(x) en violet et celui de g-1 en vert. Quel est le nombre de solutions des équations réelles suivantes ? Pour trouver ce nombre, on considère la fonction f(x), qui à x associe x, dont le graphe est la parabole représentée à droite en bleu. La fonction g1(x) associe à x la valeur 2.x +1 (la droite rouge). Les solutions de l'équation sont les abscisses des intersections de la parabole avec la droite rouge, la représentation graphique montre l'existence de deux solutions, car il existe deux intersections. Pour l'équation (2), considérons la fonction g–2(x) qui à x associe 2x – 2 (la droite violette). Elle ne rencontre pas la parabole et l'équation n'admet pas de solution. Pour traiter le dernier cas, on considère la fonction g–1(x) qui à x associe 2x – 1 (la droite verte) ; c'est encore une droite parallèle à la précédente et cette fois-ci il existe une unique solution. Une manière globale de résoudre ces trois questions est de faire appel à une lettre a qui représente un nombre quelconque. Les trois équations précédentes correspondent à la suivante, si a est égal à 1, –2 ou encore à –1 :
L'équation (4) ci-contre est dite « équation paramétrée » et la lettre a désigne le « paramètre ». Son usage permet d'étudier les équations par familles.
Problèmes soulevés par une équation
Démontrer l'existence d'une solution au problème isopérimétrique, revient à montrer l'existence d'un sommet sur la figure. À chaque couple (C, φ), on associe l'aire du triangle de périmètre 3, contenant un côté de longueur C et un angle adjacent à ce côté égal à φ. Les mathématiciens de l'antiquité ne disposaient pas d'outils pour résoudre cette question.
Les questions que soulève l'étude d'une équation dépendent de sa nature. À l'image de l'équation précédente, certaines sont définies à l'aide d'une fonction f : ℝ → ℝ, c'est-à-dire de l'ensemble des nombres réels dans lui-même. L'équation s'écrit f(x) = 0. On commence parfois l'étude par établir l'existence ou non de solution à l'équation. Le nombre de solutions est donnée par l'étude de la fonction f, ce cas est étudié dans le paragraphe sur les zéros d'une fonction.
Parfois, il est plus simple de commencer par étudier les propriétés de la ou des éventuelles solutions, sans se préoccuper initialement de leur existence. C'est le cas pour le problème isopérimétrique du triangle. La question revient à trouver le triangle de périmètre donné (on prend ici la valeur 3) de plus grande aire possible. Si T désigne l'inconnue, ici un triangle de périmètre 3, S(T) la fonction qui à un triangle associe son aire et m la borne supérieure des surfaces des triangles de périmètre 3, la traduction sous forme d'équation du problème s'écrit :

Dès l'antiquité, les mathématiciens savent que l'unique réponse possible est le triangle équilatéral. En revanche, établir l'existence d'une solution est plus technique et fait appel à des outils inconnus jusqu'au XVIII siècle. L'existence d'une solution est intimement liée à l'ensemble dans lequel on recherche cette solution. Si, dans l'exemple choisi, cet ensemble est étendu à celui des polygones de périmètre 3, l'équation n'admet plus de solution. Pour établir ce résultat, on démontre dans un premier temps qu'une éventuelle solution serait nécessairement un polygone régulier. Or plus le nombre de côtés d'un polygone régulier de périmètre donné augmente, plus son aire croît ; ce qui montre l'absence de solution, car aucun polygone régulier n'est d'aire maximale.
La forme d'une solution dépend des besoins. L'équation définissant le nombre d'or φ est : X – X – 1 = 0. Pour un architecte, la forme la plus pragmatique est une approximation décimale comme 1,618. En revanche, si l'objectif est d'établir la formule reliant la suite de Fibonacci (un) avec φ :

Une forme exacte comme (1 + √5)/2 est indispensable. Comme le nombre d'or est irrationnel, il ne peut y avoir d'expression exacte sans l'aide d'une fonction auxiliaire comme la racine carrée, car les quatre opérations et les nombres entiers n'expriment que des rationnels. L'approximation de solutions fait l'objet de vastes études, qui entrent dans un domaine des mathématiques appelé analyse numérique.
Algèbre
Théorie des équations
Le graphe du module du polynôme X - 3X + 2, montre que ce polynôme admet au moins quatre racines (la cinquième n'est pas visible sur le graphique), illustrant le théorème de d'Alembert-Gauss dans un cas particulier.
La première théorie des équations ne concerne que les équations polynomiales, c'est-à-dire de la forme P(X) = 0 où P est un polynôme. Elle est basée sur des transformations des membres de l'équation en appliquant les cinq opérations « classiques » (addition, multiplication, soustraction, division et extraction de racine) aux coefficients de l'équation comme à son inconnue.
Si le degré du polynôme est égal à 2 et si les coefficients et les solutions recherchées sont réels, alors ces méthodes permettent de trouver les solutions, encore appelées racine (cf. l'article « Équation du second degré »). L'usage du changement de variable permet d'étendre la famille d'équations qui se résolvent, comme l'illustre l'exemple e – (e + e)e + e = 0 en posant X = e. Cette méthode du changement de variable ne se limite pas aux équations algébriques.
Pour aller plus loin et résoudre l'équation cubique, c'est-à-dire du troisième degré, les mathématiciens italiens de la Renaissance découvrent la nécessité d'enrichir l'ensemble des nombres en lui adjoignant des nombres imaginaires. Cette découverte permet la résolution des équations du troisième et quatrième degré (voir les méthodes de Cardan et Ferrari).
Le théorème de d'Alembert-Gauss précise que tout polynôme de degré supérieur ou égal à 1 et à coefficients réels ou complexes, admet au moins une racine complexe. Si ce théorème assure, dans un cas très général, l'existence d'une solution, il n'en offre aucune formulation explicite, et l'intuition de ces racines complexes pour les polynômes réels n'est pas immédiate. Le deuxième théorème, dit théorème d'Abel en explique la raison : il n'existe, en général, aucune formule analogue à celles qui s'appliquent aux petits degrés, capable d'exprimer les racines. Ce résultat, œuvre de Niels Abel, est complété par Évariste Galois qui indique une condition nécessaire et suffisante pour déterminer dans quels cas les racines d'une équation polynomiale possèdent une expression de cette nature. Sa démonstration fait appel à la théorie de Galois.
Les deux théorèmes précédents closent la théorie des équations. Cette expression fut encore en vigueur en mathématiques pendant tout le XIX siècle. Elle reste d'actualité en histoire des sciences. Elle est encore utilisée en mathématiques, mais elle est devenue rare et un peu désuète.
Système d'équations linéaires
Les Neuf Chapitres sur l'art mathématique est un livre anonyme en chinois proposant une méthode de résolution de l'équation linéaire.
Une autre famille d'équations est traitée par l'algèbre : celle des équations linéaires. Ce sont les équations de la forme (1) a(x) + b = 0, où a est une application linéaire d'un espace vectoriel E dans un espace vectoriel F, b un vecteur de F et x une variable qui décrit l'ensemble E. Si les espaces E et F sont de dimension finie, notés n pour E et m pour F, le choix d'une base de E et de F, permet d'exprimer a sous la forme d'une matrice (aj,k), x sous la forme d'un vecteur colonne à n coordonnées (xk) et b d'un vecteur colonne à m coordonnées (bj).
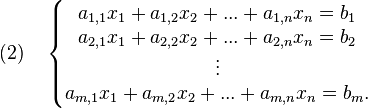
D'une équation (1) on passe à un système (2), de m équations à n inconnues. Cette technique, consistant à passer d'une équation vectorielle à un système de plusieurs équations réelles de plusieurs variables réelles, ne se limite pas au cas linéaire.
Sous la forme (2), plusieurs algorithmes permettent de trouver une racine. Si n est égal à m et si le déterminant de la matrice de a est non nul, il est possible d'utiliser la règle de Cramer. Ce n'est pas l'algorithme le plus efficace : la méthode du pivot de Gauss est plus simple et plus rapide. Elle revient à isoler les n variables à l'aide d'une suite de substitutions. Cette méthode est ancienne ; on en trouve un équivalent dans le chapitre 8 du livre chinois de mathématiques intitulé Les Neuf Chapitres sur l'art mathématique et datant d'avant notre ère. Au XIII siècle, Qin Jiushao va plus loin et trouve comment résoudre un système linéaire avec des congruences comme coefficients, pour résoudre une question liée à un « programme de répartition de grains ».
Équation linéaire et géométrie
La géométrie permet de trouver des algorithmes de résolution de l'équation linéaire, plus rapides que la méthode du pivot de Gauss. La figure illustre le graphe en dimension 3, de la fonction f.
Cette figure illustre les courbes de niveaux en bleu de la fonction f. Les segments rouges et verts correspondent au trajet suivi par la suite approximante, qui converge en deux étapes en dimension 2.
L'approche géométrique de l'équation linéaire offre des informations d'une autre nature. L'image d'une application linéaire a, c'est-à-dire l'ensemble des vecteurs qui admettent un antécédent par f forme un sous-espace vectoriel, comme l'est un plan dans un espace de dimension trois. Le noyau de a, c'est-à-dire les vecteurs de l'ensemble de départ ayant pour image le vecteur nul, est aussi un sous-espace. Ces résultats montrent que l'ensemble des solutions forme un espace affine de direction le noyau de a.
Le point de vue géométrique permet d'élaborer des algorithmes de résolution qui tiennent compte des spécificités de a. Dans certains cas particuliers, il existe des techniques qui permettent de trouver une solution plus rapidement qu'avec la méthode du pivot de Gauss. Un exemple correspond au cas où E est un espace euclidien égal à F et a est tel que l'application qui à x et y associe 〈–ax,y〉 soit un produit scalaire. Ici les crochets désignent le produit scalaire initial de l'espace E. Ceci implique que la matrice de a est de déterminant non nul et symétrique, si la base de E est choisie orthonormale.
Une méthode consiste à ne pas chercher à résoudre l'équation ax + b = 0 mais à répondre à une autre question, d'apparence plus complexe. Elle revient à trouver le point optimal de l'expression qui à x associe f(x), défini par :
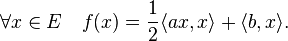
Son point optimal est la solution de l'équation linéaire. Pour comprendre la méthode de résolution, le plus simple est de représenter le cas où F est de dimension 2. Le graphe de f a alors la forme d'un pain de sucre, comme illustré sur la figure de gauche. Une méthode consiste à partir d'un point quelconque x0 et à suivre la ligne de plus grande pente, illustrée en rouge sur les figures et qui correspond à une parabole à gauche et à un segment à droite. Le sommet de cette parabole est noté x1. À partir du point x1, on suit à nouveau la ligne de plus grande pente, en vert sur les figures. Cette technique porte le nom d'algorithme du gradient.
Si, au lieu de suivre exactement le chemin de plus grande pente, on en choisit un de direction orthogonale aux directions précédentes pour le produit scalaire 〈–ax,y〉, la méthode converge vers la solution en un maximum de n étapes, si n désigne la dimension de E. Elle porte le nom de méthode du gradient conjugué.
Géométrie
Géométrie analytique
Une conique est toujours l'intersection d'un plan et d'un cône de révolution.
En géométrie euclidienne, il est possible d'associer à chaque point de l'espace un jeu de coordonnées, par exemple à l'aide d'un repère orthonormé. Cette méthode permet de caractériser des figures géométriques à l'aide d'équations. Un plan dans un espace de dimension 3 s'exprime comme l'ensemble des solutions d'une équation du type ax + by + cz + d = 0, où a, b, c et d sont des nombres réels, x, y, z les inconnues qui correspondent aux coordonnées d'un point du plan dans le repère orthonormal. Les valeurs a, b et c sont les coordonnées d'un vecteur perpendiculaire au plan défini par l'équation. Une droite s'exprime comme l'intersection de deux plans, c'est-à-dire comme les solutions d'une équation linéaire à valeurs dans ℝ ou comme les solutions d'un système de deux équations linéaires à valeurs dans ℝ, si ℝ désigne l'ensemble des nombres réels.
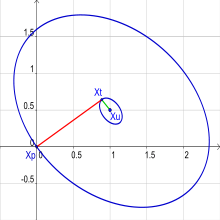
L'équation cartésienne offre une méthode simple de démonstration du théorème de Thalès relatif au cercle.
Une conique est l'intersection d'un cône d'équation x + y = z et d'un plan. Autrement dit, dans l'espace, toute conique est définie comme les points dont les coordonnées sont solutions d'une équation du plan dans ℝ et de l'équation précédente. Ce formalisme permet de déterminer les positions et les propriétés des foyers de la conique.
Avec cette approche, on obtient des équations dont l'objectif n'est pas l'expression des solutions au sens du paragraphe précédent. Un exemple est donné par le théorème de Thalès indiquant qu'un triangle est rectangle s'il possède un côté égal à un diamètre d'un cercle et un sommet opposé élément du cercle. Ce théorème est illustré sur la figure de droite. Si le repère est bien choisi, il est orthogonal et l'équation du cercle s'écrit : x + y = 1, les points A et C de la figure de droite ont pour coordonnées respectives (-1,0) et (1,0). Dire que AB est perpendiculaire à CB revient à dire que les vecteurs associés sont orthogonaux. L'équation du cercle permet de conclure la démonstration, en effet :
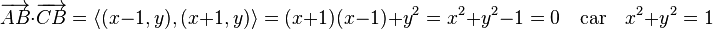 .
.
L'usage d'une équation permet de faire appel à un nouveau pan des mathématiques pour résoudre des questions de géométrie. Le repère cartésien transforme un problème de géométrie en un problème d'analyse, une fois les figures étudiées traduites en équations ; d'où le nom de géométrie analytique. Ce point de vue, mis en évidence par Descartes, enrichit et modifie la géométrie telle que la concevaient les mathématiciens de la Grèce antique.
Actuellement, la géométrie analytique désigne une branche des mathématiques où la recherche est active. Si elle utilise toujours l'équation pour caractériser une figure, elle utilise aussi des outils sophistiqués issus de l'analyse fonctionnelle ou de l'algèbre linéaire.
Équation cartésienne et paramétrique
Il existe au moins deux méthodes pour décrire une figure géométrique à l'aide d'équations. La première consiste à la décrire par une équation de la forme f(x) = 0, où f est une fonction de l'espace euclidien E de dimension n dans ℝ où d est un entier plus petit que n. Si f est une fonction suffisamment régulière, n - d est la dimension de la figure géométrique. Si elle est égale à 1, la figure est une courbe, pour 2, on parle de surface, etc. Une telle équation peut aussi s'écrire comme système de d équations à valeurs dans les réels exactement comme pour le cas de l'équation linéaire. Ce type d'équation est appelé cartésien si x est exprimé à l'aide de ses coordonnées dans un repère cartésien. Les équations décrites dans le paragraphe précédent sont toutes cartésiennes, comme celle du cercle d'équation x + y = 1.
Une autre méthode consiste à décrire la figure géométrique à l'aide d'une fonction f de ℝ dans E de la manière suivante, un point m de E est élément de la figure lorsqu'il existe un point x de l'ensemble de définition de la fonction f tel que f(x) est égal à m. Dans ce cas, et sous réserve d'une régularité suffisante de f (il suffit que sa différentielle soit injective), la figure est de dimension d. On parle d'équation paramétrique de la figure géométrique, cette définition de l'équation est relativement éloignée de celle trouvée en algèbre.
Exemple : Le cercle trigonométrique du plan euclidien admet pour équation paramétrique, de paramètre θ.
Si la figure est suffisamment régulière, par exemple si elle correspond à une variété, au moins localement, il existe un paramétrage de la figure. Localement signifie que si m est un élément de la figure, il existe une fonction f et un voisinage V d'un point de l'ensemble de départ de f tel que l'image de f soit incluse dans la figure et tel que l'image de V par f soit un voisinage de m dans la figure. Localement, il est aussi possible de définir la figure à l'aide d'une équation cartésienne.
Arithmétique
Équation diophantienne
Après plusieurs siècles d'efforts de la communauté mathématique, c'est David Hilbert qui finit par résoudre l'équation diophantienne de degré 2.
Historiquement, les premières équations formalisées sont de nature arithmétique et datent du III siècle. Si l'on recherche comme solution d'une équation, non pas un nombre quelconque, mais un nombre entier et si l'équation est à coefficients entiers, on parle d'équation diophantienne. Les méthodes décrites précédemment sont généralement insuffisantes pour conclure, des outils issus de l'arithmétique, ou au moins de l'arithmétique élémentaire sont indispensables. Un exemple relativement simple est celui linéaire à deux inconnues ax + by = c.
Si le degré de l'équation augmente, la question devient beaucoup plus complexe. Même une équation de degré 2 n'est en général pas simple (voir par exemple le théorème des deux carrés de Fermat ou l'équation de Pell-Fermat). À condition d'ajouter d'autres méthodes, comme celle de descente infinie et de nouveaux résultats comme le petit théorème de Fermat, il est possible de résoudre quelques cas particuliers. Le cas général de l'équation de degré 2 demande l'usage d'outils plus sophistiqués, comme ceux de la théorie algébrique des nombres. Les ensembles de nombres sont enrichis, on utilise les corps finis et les entiers algébriques, qui s'étudient, comme pour l'équation algébrique, à l'aide de la théorie de Galois. Si l'équation algébrique de degré 2 est essentiellement résolue par Al-Khawarizmi, un mathématicien arabe du VIII siècle, il faut attendre la fin du XIX siècle pour que David Hilbert vienne à bout de son équivalent diophantien. L'étude de l'équation diophantienne est souvent suffisamment complexe pour se limiter à établir l'existence de solutions et, s'il en existe, à déterminer leur nombre.
Un vaste domaine d'application des équations diophantiennes est l'informatique. Les outils issus de leurs études permettent de concevoir des codes correcteurs et sont à la base d'algorithmes en cryptologie. Il existe des équations diophantiennes qui s'écrivent simplement, mais qui demandent des temps de traitement prohibitifs pour les résoudre, elles sont à la base de codes secrets. Par exemple, l'équation n = xy, où n est un entier naturel fixé et où x et y sont les inconnues, n'est pas résoluble en pratique, si n est le produit de deux nombres premiers suffisamment grands. Cette équation est à la base du code RSA.
Nombre algébrique et transcendant
Lindemann montre qu'aucune équation polynomiale à coefficients entiers n'admet π comme racine.
Au lieu de se demander quels nombres sont solutions d'une équation donnée, on peut considérer le problème inverse : de quelles équations un nombre donné est-il solution ? Un nombre est dit rationnel s'il est solution d'une équation du premier degré à coefficients entiers. Il est dit algébrique s'il est solution d'une équation polynomiale à coefficients entiers. S'il n'est pas algébrique il est dit transcendant. Ainsi, pour un nombre donné, l'objectif est de trouver les éventuelles équations polynomiales dont ce nombre est racine (voir l'article « Polynôme minimal d'un nombre algébrique »).
Par exemple pour √2, la question se pose de savoir s'il est possible de construire une équation du premier degré ayant cette valeur pour racine. Elle se résout simplement : si une telle équation existe, on en déduit l'expression 2a = b, où a et b sont des nombres entiers. L'analyse de la décomposition en facteurs premiers montre que le terme de droite contient le facteur 2 un nombre pair de fois et celui de gauche un nombre impair. Cette remarque démontre que √2 n'est pas un nombre rationnel. En revanche, il est par définition algébrique, car solution de l'équation X – 2 = 0.
La même question pour le nombre π est plus délicate. Pour montrer que ce nombre n'est solution d'aucune équation du premier degré à coefficients dans les nombres entiers, on utilise des fractions continues généralisées (une démonstration est proposée dans l'article « Fraction continue et approximation diophantienne »). Les techniques sont plus sophistiquées que celles utilisées pour démontrer l'irrationalité de √2. Alors que ce premier résultat est déjà connu à l'époque d'Euclide, il faut attendre le XVIII siècle pour établir celle de π.
Si montrer que π n'est pas solution d'une équation du premier degré à coefficients dans les entiers n'est déjà pas si simple, il est encore plus ardu de montrer qu'il n'est solution d'aucune équation polynomiale à coefficients entiers. Il faut encore plus d'un siècle d'efforts pour établir cette transcendance. Elle clôt une vieille question, à savoir s'il est possible de construire à la règle et au compas un carré de même aire qu'un cercle, cette question porte le nom de quadrature du cercle. Elle est impossible car toute construction de cette nature définit une surface d'aire égale à un nombre algébrique.
Géométrie algébrique
Genre de quelques surfaces orientables
genre 0
genre 1
genre 2
genre 3
Résoudre une équation diophantienne polynomiale n'est pas toujours possible avec les seuls outils de la théorie algébrique des nombres. Avec ce type de méthode, Ernst Kummer parvient à résoudre, au milieu du XIX siècle, presque tous les cas inférieurs à 100 de la célèbre équation dénommée dernier théorème de Fermat, mais le cas général reste hors de portée.
La géométrie, et plus précisément la géométrie algébrique, est nécessaire pour conclure. L'équation du dernier théorème de Fermat s'écrit de la manière suivante x + y = z. Quitte à étudier les solutions dans les nombres rationnels, on peut diviser par z et écrire l'équation q + r = 1. Si q et r sont choisis dans l'ensemble des nombres complexes, noté ici ℂ, géométriquement, cette équation correspond à une figure de ℂ, ou encore à une surface réelle dans un espace de dimension 4. Vue dans l'espace projectif de ℂ, on obtient une surface réelle, plongée dans un espace compact dont la visualisation n'est pas intuitive. Il suffit de connaître les points rationnels de cette surface pour permettre de conclure sur les solutions du théorème de Fermat.
La topologie offre des éléments de réponse pour cette équation. Une surface de cette nature possède un genre. Topologiquement, elle est équivalente à une sphère (genre 0), à un tore (genre 1) ou à une figure comportant n trous (genre n). Dans le cas d'une variété algébrique, définie par une équation du type P(X, Y), où P est un polynôme à coefficients rationnels, le genre de la variété est une indication sur le nombre de solutions. Ce résultat, qui porte le nom de théorème de Faltings, est de la même famille d'outils que ceux utilisés pour la démonstration du théorème de Fermat.
Analyse
Zéro d'une fonction
La dichotomie Le théorème du point fixe La méthode de Newton.
En analyse plus encore, il sera bien souvent vain d'espérer traiter une équation par des techniques élémentaires de substitution ou transformation, en espérant isoler la variable. Et même quand cela s'avère possible, comme pour certaines équations algébriques, si l'objectif est l'obtention d'une valeur numérique, l'approche décrite dans ce paragraphe est souvent moins coûteuse. On peut toujours ramener l'équation à une forme f(x) = 0. Considérons par exemple l'équation suivante, l'inconnue étant un réel strictement positif :

Elle se réécrit f(x) = 0 si l'on pose f(x) = (sinx) + (lnx)/2. Un zéro est une solution de l'équation dans ce cas particulier. Il serait vain de chercher à exprimer un zéro par une formule composant des fonctions élémentaires (fractions rationnelles, fonctions exponentielles, logarithmiques ou trigonométriques...). Une telle expression n'existe pas ici. On se contentera de chercher le nombre de zéros, des intervalles les contenant, ainsi que des approximations de ces zéros.
Dans l'exemple, l'étude de la fonction f montre facilement qu'il y a exactement trois zéros, un dans l'intervalle ]0, 1], un dans [3, 4] et le dernier dans [5, 6]. La continuité de f permet de construire une première suite (xn) convergeant vers le zéro de l'intervalle ]0, 1]. Au voisinage de 0, la fonction est strictement négative, au point 1, elle est strictement positive, le théorème des valeurs intermédiaires garantit l'existence d'un zéro dans cet intervalle, car f est continue. On pose x0 = 0, au point 1/2, la fonction f est strictement positive, on en déduit l'existence d'un zéro dans l'intervalle [0, 1/2] et on pose x1 = 0. Au point 1/4, elle est strictement négative, on en déduit l'existence d'un zéro dans [1/4, 2/4] et on pose x2 = 1/4 et ainsi de suite. On construit ainsi une suite convergeant vers la solution, ce qui permet d'obtenir une approximation aussi précise que souhaitée. Cette méthode porte le nom de dichotomie et est la première illustrée dans la figure du paragraphe.
Seule la continuité de f a été utilisée dans l'algorithme précédent, un théorème du point fixe est à la base d'une méthode plus efficace. On construit une fonction g (en rouge sur la figure du milieu) ayant pour point fixe (c'est-à-dire un point x tel que g(x) = x) la solution recherchée. On choisit g de telle manière que la dérivée au point fixe soit la plus petite possible. Une solution simple est de définir g(x) = x + λf(x). Dans l'exemple, on peut choisir λ égal à –1/2. Cette fois-ci, il est plus judicieux de choisir x0 égal à 1. On définit xn = g(xn–1). Si la dérivée de g est proche de 0, la convergence est bien meilleure que celle de l'algorithme précédent. Dans l'exemple choisi, la solution est égale à 0,43247... La quatrième itération de la première méthode donne pour valeur 0,375 alors que celle issue du point fixe donne 0,4322...
La dérivabilité de f partout sur son domaine permet la mise au point d'un algorithme ayant une convergence encore meilleure. La méthode consiste, à partir d'un point x0, égal à 1 dans l'exemple, à trouver la solution x1 de l'équation linéaire tangente de la fonction f au point x0. Puis on construit x2 comme la solution de l'équation linéaire tangente de la fonction f au point x1. Dans l'exemple étudié, illustré sur la figure de droite, la valeur de x4 est égale à 0,43246 soit quatre décimales exactes. Cette méthode porte le nom de Newton.
Équation vectorielle
.png)
L'algorithme du gradient s'applique à toute équation d'un espace vectoriel de dimension finie et à valeurs dans l'ensemble des nombres réels. Il est illustré ici à l'aide d'une représentation en courbes de niveaux
Si l'équation prend la forme f(x) = 0 où f est une fonction d'un espace vectoriel E à valeurs dans un espace vectoriel F dont le vecteur nul est noté 0, les idées de l'algèbre linéaire peuvent encore s'appliquer partiellement. Il est possible de choisir une base de E et de F et d'exprimer f à l'aide de m fonctions fj réelles de n variables xk, où m est la dimension de F et n celle de E, on obtient ce que l'on appelle un système d'équations, de la forme suivante :
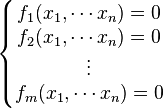
.png)
Cette représentation correspond à la même équation que celle représentée à gauche, mais cette fois-ci en dimension 3.
Les mêmes limitations que celles décrites au paragraphe précédent s'appliquent. Il est tout à fait possible que la technique d'isolation des variables, qui fonctionne dans le cas de l'équation linéaire, ne soit pas possible, par exemple si les fi contiennent des expressions trop complexes. Certaines des idées, exprimées dans le cas où f est une fonction de la variable réelle à valeurs réelles, peuvent s'adapter à la géométrie d'un espace vectoriel de dimension finie, d'autres non. Il n'existe pas d'équivalent du théorème des valeurs intermédiaires pour la nouvelle configuration. En revanche, le théorème du point fixe se généralise, ainsi que la définition d'une dérivée.
La dérivée, ou plutôt la différentielle de f peut être utilisée de plusieurs manières. La première est une simple adaptation de la méthode de Newton, à partir d'un point x0, on résout l'équation linéaire tangente en ce point, c'est-à-dire Dfx0.h + f(x0) = 0. La valeur x1 est égale à x0 + h et l'on réitère le processus pour obtenir une suite. Si E est égal à F et pour permettre une convergence plus rapide, on résout souvent une équation linéaire analogue, mais dont l'application linéaire associée définit un produit scalaire. Cette astuce permet une accélération du temps de traitement de la résolution des équations linéaires intermédiaires, la méthode associée porte le nom de quasi-Newton.
Une autre méthode consiste à transformer l'ensemble d'arrivée en R+, par exemple en équipant F d'un produit scalaire et en recherchant les zéros de la fonction g à valeurs réelles, qui à x associe le carré de la norme de f(x) ou encore le produit scalaire de f(x) avec x, si E est égal à F. Les deux équations f(x) = 0 et f(x) = 0 possèdent les mêmes solutions. Le problème revient à trouver un extremum de la nouvelle fonction g. On part d'un point x0 dans la direction de la ligne de plus grande pente, dont la direction est donnée par le gradient et on s'arrête au point x1, le minimum de la fonction g dans la direction du gradient. Puis on réitère le calcul.
Analyse fonctionnelle
L'aérodynamisme d'un objet volant est régi par une équation qui s'étudie à l'aide de l'analyse fonctionnelle. Des outils puissants tels que l'espace de Hilbert sont nécessaires pour établir quelques théorèmes généraux.
Si l'espace vectoriel E est plus vaste et n'est plus de dimension finie, d'autres idées doivent être utilisées pour venir à bout de l'équation. Cette configuration se produit si l'inconnue x désigne une fonction. Une fois encore, il est vain de rechercher des méthodes systématiques exprimant les solutions sous la forme d'une composition de fonctions élémentaires, les cas où une telle expression existe tiennent plus de l'exception que de la règle.
Une méthode générale consiste associer à un espace de fonctions Hp, comme celui des fonctions continues définies sur un intervalle [a, b], une géométrie. Pour ce faire, on peut définir sur l'espace une distance euclidienne, c'est-à-dire définie par un produit scalaire comme celui qui, à deux fonctions f et g de Hp associe :
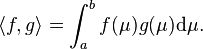
À l'aide de cette distance, on construit une suite (xn) de fonctions qui vérifie la propriété de Cauchy, c'est-à-dire que si les indices n et m sont suffisamment grands xn et xm sont arbitrairement proches. Un exemple est donnée par l'équation intégrale, dite de Fredholm :

La suite (xn) est construite de telle manière que la distance entre les fonctions Fxn(t) et g(t) tende vers zéro. La difficulté est qu'une suite de Cauchy ne converge pas nécessairement dans Hp, ce qui revient à dire que cet espace n'est pas complet. Il est alors plongé dans un espace H qui le contient et qui lui, est complet. Un élément de H n'est plus une fonction, il peut être vu comme un élément du dual de Hp. Dans H, la suite (xn) converge vers une limite s. Elle peut être interprétée comme une solution de l'équation (1) car la distance entre F(s) et g est nulle. Mais s n'est pas une fonction, c'est un être abstrait, élément du dual de Hp, on parle de solution faible. On montre enfin que cet être abstrait s'identifie à un élément de Hp, c'est-à-dire une à fonction qui vérifie l'équation (1), appelée solution forte
Systèmes dynamiques
Introduction
Une fois connues la vitesse et la position d'une comète en un instant t, la résolution d'une équation différentielle permet de déterminer sa trajectoire exacte.
La physique est à l'origine d'équations fonctionnelles particulières : les systèmes dynamiques. Un exemple historiquement célèbre, est issu de la loi universelle de la gravitation. Si l'on néglige l'attraction due aux autres planètes, l'accélération de la Terre est dirigée vers le soleil et son intensité est inversement proportionnelle au carré de la distance qui sépare les deux astres. Cette loi physique se traduit par une équation qui, une fois connues la position et la vitesse initiales de la Terre, donne sa trajectoire, c'est-à-dire sa position en fonction du temps. Historiquement, la capacité à prévoir la position exacte des comètes au XVIII siècle fut une confirmation de la théorie de Newton.
Un système qui évolue et dont une équation permet de connaître exactement son état au cours du temps, à la condition de connaître son état initial, est qualifié de dynamique. On peut les classer en trois grandes catégories. La formulation la plus simple est dite discrète, l'état du système est décrit à différentes étapes, notées par les entiers 0, 1, 2 ..., k, ... et la solution est une suite (uk). Ce type de système est utilisé pour simuler un comportement continu, en discrétisant le temps à l'aide d'intervalles suffisamment petits pour que l'imprécision engendrées par cette méthode reste dans des limites acceptables. Connaître la trajectoire exacte d'une comète suppose la prise en compte de l'attraction de tous les corps célestes du système solaire. Résoudre l'équation dans ce cas devient difficile, on peut alors supposer qu'en une seconde, la gravité est presque constante, la trajectoire de la comète est presque parabolique et sa position au bout d'une seconde se calcule aisément, une fois connue la position des différents corps célestes massifs comme les planètes ou le soleil. Ensuite, il suffit de recalculer, à chaque seconde, la nouvelle attraction pour obtenir une suite donnant une approximation de la trajectoire réelle. Si (pk, vk) désigne le couple position et vitesse de la comète à la seconde k, il existe deux fonctions f et g régissant l'équation :

On obtient des suites définies par récurrence, caractéristique d'un système dynamique discret.
Il est aussi possible de s'y prendre autrement. Une relation lie la position de la comète avec sa vitesse instantanée (que l'on appelle dérivée en mathématiques) et son accélération (ou dérivée seconde). Résoudre l'équation permet de trouver la trajectoire de notre planète. L'équation prend une forme de la nature suivante, appelée équation différentielle :
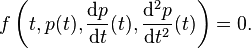
Enfin, l'objectif peut être de déterminer l'état d'un objet qui ne se traduit non pas par un vecteur d'un espace de dimension finie, mais par une fonction, comme l'état d'une corde vibrante. On parle d'équation aux dérivées partielles.
Équation différentielle

Tracé d'une solution d'une équation différentielle (bleu) de la forme x' = φ(x), la fonction φ est illustrée en vert.
La lettre x désigne ici une fonction de la variable réelle et f une fonction de n + 1 variables réelles. Soit F la fonction qui à x associe la fonction t ↦ f(t, x(t), x'(t), x(t),..., x(t)), où x la dérivée k de la fonction x. On considère l'équation F(x) = 0. Une telle équation est appelée équation différentielle.
Les solutions sont, en général, étudiées sous la « forme de Cauchy », c'est-à-dire associées à des valeurs t0 ,ξ0 ,ξ1,... ,ξn–1 telles qu'une solution vérifie :
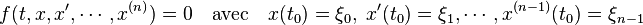
La situation est un peu analogue à celle des équations polynomiales. Il existe une théorie des équations différentielles. Un premier résultat global est le théorème de Cauchy-Lipschitz, qui garantit que si f est une fonction lipschitzienne, il existe une unique solution au problème de Cauchy. Résoudre le problème de Cauchy consiste à déterminer la solution d'une équation différentielle vérifiant une condition initiale donnée. Dans certains cas particuliers, il est possible d'expliciter directement une solution, comme pour l'équation différentielle d'ordre un à variables séparées ou l'équation différentielle linéaire, mais pas toujours.
L'exemple de droite illustre une solution d'une équation de la forme x' = φ(x), où la solution recherchée est une fonction définissant une courbe du plan. Sa variable est réelle et elle est à valeurs dans R. La fonction φ est une fonction continue de R dans lui-même. À chaque point du plan, elle associe un vecteur, elle est dite champ vectoriel. Une solution s possède la propriété d'avoir, pour chaque point p de son image, une tangente à sa courbe de direction φ(p). La vitesse scalaire à l'instant t est égale à la norme de l'image par φ du point s(t).
Équation aux dérivées partielles

L'équation régissant la surface de la mer est une équation aux dérivées partielles.
La physique propose divers exemples où la solution recherchée ne dépend pas d'une mais de plusieurs variables. Un cas relativement simple est celui d'une onde sur une corde vibrante. La fonction décrivant sa position dépend de deux paramètres, le temps et une coordonnée pour décrire un point de la corde. Trois variables sont nécessaires pour décrire une vague, deux décrivent la position d'un point de la surface et la troisième le temps. En physique quantique, la relation fondamentale de la dynamique se traduit par une équation d'onde qui nécessite quatre variables, trois pour l'espace et une pour le temps. Ce principe fondamental est appelée équation de Schrödinger.
L'équation équivalente à celle du paragraphe précédent, pour une fonction x de plusieurs variables, porte le nom d'équation aux dérivées partielles. L'équivalent du problème de Cauchy s'exprime de manière plus complexe. la condition initiale est remplacée par les conditions aux limites. Dans certains cas on recherche comme solution une fonction définie sur Ωx[a, b] où Ω est un ouvert que l'on suppose borné, connexe et dont la frontière ∂Ω est régulière, [a, b] est un intervalle qui représente le temps. Les conditions aux limites s'expriment sous forme de deux contraintes. L'une correspond à la valeur ou la limite de la fonction sur ∂Ω×]a, b[. La fonction modélisant les mouvements d'une membrane de tambour est constante à la limite de la membrane, cette contrainte est appelée la condition aux limites de Dirichlet. Les valeurs de la fonction sur Ωx{a} sont appelées la condition initiale ou donnée de Cauchy.
En météorologie, la prévision numérique du temps consiste à modéliser les mouvements de l'atmosphère terrestre par l'équation de Navier-Stokes. Une difficulté pratique est de déterminer précisément la donnée de Cauchy : il faudrait mesurer la température, la pression, le taux d'humidité etc en tout point de l'atmosphère. Cette difficulté, ajoutée au fait qu'on ne sache pas résoudre l'équation de Navier-Stokes, font que les méthodes de résolution utilisées sont numériques : on ne peut calculer que des valeurs approchées.
Certaines équations aux dérivées partielles ne sont pas aussi complexes. Fourier, un mathématicien du début du XIX siècle avait trouvé comment la chaleur se diffuse dans un corps solide dans le cas de conditions aux limites simples. La spécificité de cette équation, comme celle décrivant les ondes se propageant sur une corde vibrante est d'être linéaire, c'est-à-dire que l'on peut la mettre sous la forme a(x) + b = 0, où a est un opérateur linéaire construit à l'aide de dérivées partielles et b une fonction particulière. Le cas linéaire est traité par une théorie « relativement bien constituée ». L'outil principal est un espace fonctionnel particulier, dit de Sobolev.
D'autres équations restent difficiles d'accès. La surface d'un océan est aussi modélisée par une équation aux dérivées partielles. Comme le laisse penser la forme d'une vague, l'expression d'une solution peut s'avérer difficile. On est loin de disposer d'une théorie générale, les deux paragraphes suivant indiquent le type de difficulté à résoudre pour comprendre les systèmes dynamiques.
Condition initiale
La frontière d'un ensemble de Julia est le plus souvent un fractal.
Une des questions qui se pose sur les systèmes dynamiques est la nature de la solution en fonction de sa valeur initiale. Si une petite modification de cette valeur change de manière importante le comportement de la solution, même si le système est déterministe, son évolution semblera aléatoire. Si "déterministe" signifie que toute évolution du système dépend uniquement de sa valeur initiale, sa connaissance parfaite permet de prévoir parfaitement son futur, ce qui est toujours le cas d'un système dynamique idéalisé. En physique, il est impossible de connaître parfaitement l'état initial du système. On le connaît, par exemple avec une précision de 5 décimales, si la sixième décimale finit par modifier l'évolution du système de manière significative, le futur de l'évolution n'est pas connu (il est même indéterminable), mais dépend d'une information inaccessible parce qu'idéalisée. Le futur apparaît alors comme incertain, même si les lois modélisant l'évolution sont "déterministes". On voit donc ici les limites de la modélisation. Ce phénomène se produit en météorologie, cette science est modélisée par un système dynamique qui, pour permettre une prévision sur le long terme, demande une connaissance précise de l'état initial. Comme cette connaissance est d'une précision limitée, il existe un horizon (ou plutôt des horizons plus ou moins divergents) dans la prévision. Si l'équation modélisant la météorologie est bien connue, on ne sait toujours pas si les solutions dépendent continûment de valeurs aux bornes du domaine de la solution (l'équivalent de la condition initiale pour une équation aux dérivées partielles), cette question est associée à l'un des sept prix de un million de dollars offerts par l'Institut de mathématiques Clay au premier qui apportera la réponse.
Une méthode pour apporter des éléments de réponse, est d'étudier les cas les plus simples possibles. On cherche à comprendre ce phénomène sur une suite récurrente définie par l'équation : xn+1 = f(xn) où f est un polynôme du second degré, réel ou complexe. Un cas très étudié est celui où f(x) = x + c. La condition initiale est ici la valeur de x0, un nombre complexe. Jc est l'ensemble des conditions initiales telles que la suite est bornée, il est appelé ensemble de Julia, dont un exemple est illustré sur la figure de gauche. Toute condition initiale p hors de la frontière de Jc possède un voisinage ne contenant que des conditions initiales dont le comportement des suites sont qualitativement analogues. Les couleurs indiquent les valeurs de convergence, l'intensité symbolise la vitesse de convergence.
Une première question qui se pose est le poids de la zone frontière. Sur cette zone, il existe toujours une perturbation de la condition initiale, aussi minime soit-elle, qui modifie la nature de la solution. Dans les configurations classiques, une frontière d'une figure géométrique de dimension 2 est d'aire nulle, même si la figure possède une aire strictement positive. Ainsi, un disque de rayon strictement positif est d'aire strictement positive et sa frontière, un cercle de même rayon, est d'aire nulle. En revanche, le cercle, considéré comme une courbe, possède une longueur finie. Pour la frontière de l'ensemble de Julia, cette méthode s'avère parfois inopérante, on peut trouver une longueur infinie, si la frontière est considérée comme une courbe. Pour évaluer le poids de cette longueur, on utilise une remarque géométrique. Soit S une surface d'aire s, l'homothétie de rapport 2 appliquée à S, définit une nouvelle surface d'aire 2s. Si V est une figure géométrique de dimension 3 et de volume v, l'homothétie de rapport 2 définit une figure de volume 2v. L'exposant que l'on applique au rapport de l'homothétie indique la dimension de la figure, ce qui, d'une certaine manière permet une évaluation du poids de la figure, on parle de dimension de Hausdorff ou de dimension fractale. Cette technique peut être appliquée à la frontière de l'ensemble de Julia, sa dimension est génériquement différente de un : la frontière est dite fractale.
Chaos
Une suite récurrente, même définie de manière simple, permet de voir l'apparition d'un phénomène chaotique.
La sensibilité à la condition initiale n'est pas l'unique question à résoudre pour élaborer une théorie générale des systèmes dynamiques. On souhaite aussi connaître le comportement limite du système, encore appelé comportement asymptotique, c'est-à-dire ce qu'il se passe une fois que l'on a attendu que le système se stabilise. S'il ne diverge pas, on peut classer son comportement en trois catégories, soit le système s'immobilise, soit il tend vers un cycle, soit vers encore autre chose qui, selon certaines définitions, est appelée chaos.
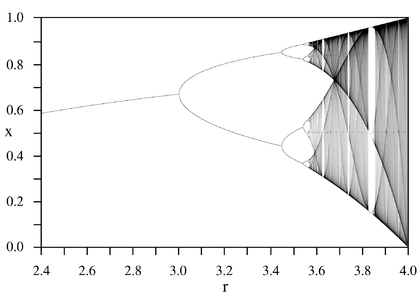
Une fois encore, il est utile de considérer le système dynamique le plus simple possible, pour comprendre au moins qualitativement les mécanismes en jeu. Comme précédemment, on utilise une suite récurrente définie par un polynôme du second degré Pr, cette fois-ci réel à valeurs réelles. La suite logistique est définie par récurrence : xr,n+1 = r xr,n(1 – xr,n). L'un des charmes de cette suite est que son comportement est relativement indépendant de la condition initiale si elle est choisie entre 0 et 1.
Les turbulences générées par les masses d'air autour d'une aile d'avion en mouvement sont chaotiques.
L'objectif est d'augmenter la valeur de r, initialement nulle et d'étudier ce comportement asymptotique. Si une fonction f possède un point fixe pf, de dérivée strictement comprise entre –1 et 1, en valeur absolue, et si la suite définie par xn+1 = f(xn) prend une valeur proche de ce point fixe, elle converge vers pf. Ce point est dit attracteur et la zone des valeurs initiales dont les suites convergent vers ce point est appelée bassin d'attraction. Pour une suite logistique le bassin d'attraction principal contient toujours ]0, 1[, à un ensemble négligeable près, quelle que soit la valeur de l'attracteur. La suite semble être attirée, comme par un aimant vers cet attracteur. Si r est compris entre 0 et 3, l'attracteur est un point et la suite converge. À partir de la valeur 3, le polynôme Pr ne possède plus de point fixe, mais le polynôme composé avec lui-même, en possède un, si r est suffisamment petit. Le comportement asymptotique de la suite est une oscillation entre les deux points fixes attractifs de Pr. La valeur 3 de r est appelée une bifurcation. L'attracteur devient un ensemble à deux éléments, illustré sur la figure de droite. Au point 1 + √6, une nouvelle bifurcation se produit, l'attracteur possède alors 4 points. Le cardinal de l'attracteur augmente de plus en plus en fonction de r par des doublements, jusqu'à atteindre une valeur infinie pour r égale à μ, qui se situe aux alentours de 3,57.
Il devient nécessaire de préciser ce qu'on entend par « attracteur » : ce sera l'intersection des ensembles An où An est l'adhérence des points x k pour k supérieur à n. Dans le cas de la suite logistique et à l'exception d'un ensemble de mesure nulle, l'attracteur est indépendant de la condition initiale. On peut voir l'attracteur Ar comme un ensemble qui attire les éléments de la suite, laquelle, à partir d'un certain rang, devient arbitrairement proche de A. Entre μ et 4, un triple comportement est possible. Pour un ensemble H (pour hyperbolique) de valeurs du paramètre r qui est un ouvert dense de [μ, 4], l'attracteur est un ensemble fini (comportement cyclique). Pour un autre ensemble C (pour chaotique) de valeurs du paramètre, qui est lui fermé, totalement discontinu et de mesure strictement positive, pour presque toutes valeurs initiales x0 (dépendant de r) l'attracteur est un intervalle d'intérieur non vide et le comportement est chaotique, c'est-à-dire qu'il évolue sans ordre apparent, à l'exception d'un ensemble de mesure nulle, semblant évoluer au gré du hasard, même si cette évolution est en fait déterministe. Le dernier comportement se produit sur l'ensemble A, complémentaire de l'union de C et de H dans [μ, 4]. L'ensemble A n'est pas vide, le comportement est alors plus complexe et fait intervenir, comme attracteur, des ensembles de Cantor. Depuis 2002, on sait que A est de mesure nulle.
Ce comportement s'applique aussi aux équations différentielles ou aux dérivées partielles. Edward Lorenz a trouvé une équation différentielle relativement simple, ayant un attracteur fractal, généralement qualifié d'étrange, il est représenté sur la deuxième illustration de cet article. Certaines équations différentielles ne peuvent avoir de solutions si complexes, le théorème de Poincaré-Bendixson montre une famille d'équations n'ayant pas de comportement chaotique. Des solutions chaotiques complexes apparaissent aussi dans les équations aux dérivées partielles, on les trouve dans les modélisations des mouvements des masses d'air, par exemple autour des ailes d'avion, elles prennent la forme de turbulences. En 2009, l'état des mathématiques est loin d'être capable de présenter une condition nécessaire et suffisante générale, indiquant si oui ou non un comportement chaotique apparaît, même dans le cas des systèmes discrets.

 词典释义:
词典释义:
 ,
,
 式; 化学式,公式
式; 化学式,公式



 式;
式;
 式
式
 ,
, 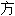
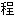 式; 等式:~du premier[du second]degré 一[二]次
式; 等式:~du premier[du second]degré 一[二]次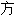
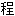 ~à plusieurs inconnues多元
~à plusieurs inconnues多元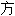
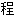 ~différentielle[intégrale]微分[积分]
~différentielle[intégrale]微分[积分]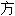
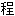 résoudre une~求解一个
résoudre une~求解一个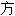
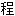 式
式
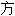
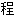
 带
带
 ; 配
; 配
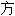
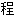
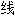
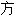
 环
环
 式
式
 续性
续性
 ; 色散
; 色散
 标
标
 性微分
性微分
 ; 矛盾
; 矛盾
 组
组
 组
组
 组相容性
组相容性

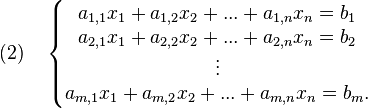

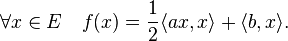
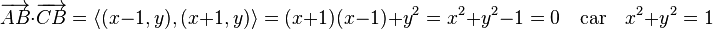 .
.

.png)
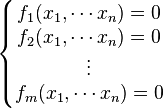
.png)