L'analyse comparative est compliquée par l'incomplétude des ensembles de données sur les indicateurs de produits et dans la mesure où selon les régions, la disponibilité des données n'est pas la même.
关于产出指标的成套数据的不完整性以及各区域中数据可获性的不均衡对进行比较分析造成一些困难。
 词典释义:
词典释义:
n. f. sentiment d'~[]空虚感, 满足感
 ]空虚感,
]空虚感,  满足感
满足感 连贯,无联系,结构松散,缺乏条理;
连贯,无联系,结构松散,缺乏条理;
 确定,
确定,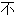 明确,
明确,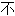 肯定;
肯定;
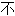 理解,
理解,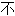 了解;
了解;
 足,贫乏,缺乏;
足,贫乏,缺乏;
 满意,
满意, 满足;
满足;
 合逻辑;
合逻辑;
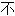 可能;
可能;
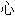 】空虚感,
】空虚感, 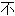 满足感
满足感
sentiment d'incomplétude〔心〕空虚感,不满足感
L'analyse comparative est compliquée par l'incomplétude des ensembles de données sur les indicateurs de produits et dans la mesure où selon les régions, la disponibilité des données n'est pas la même.
关于产出指标的成套数据的不完整性以及各区域中数据可获性的不均衡对进行比较分析造成一些困难。
On parle de complétude en mathématiques dans des sens très différents. On dit d'un objet mathématique qu'il est complet pour exprimer que rien ne peut lui être ajouté, en un sens qu'il faut préciser dans chaque contexte. Dans le cas contraire, on parle d'incomplétude, surtout dans le contexte de la logique mathématique.
Un espace métrique est complet quand toute suite de Cauchy d'éléments de cet espace converge, voir espace complet. Plus généralement, un espace uniforme est complet quand tout filtre de Cauchy converge. Un espace mesuré est complet quand tout sous-ensemble d'un ensemble de mesure nulle est mesurable, voir mesure complète. En logique mathématique, un jeu de règles ou d'axiomes est complet quand il formalise entièrement la sémantique attendue. Cela peut se préciser de façons très différentes. On a les deux notions de complétude suivantes pour la sémantique de Tarski. Un système de déduction pour une logique donnée (calcul propositionnel, ou calcul des prédicats en logique classique mais aussi en logique intuitionniste ...), est complet quand il démontre les formules valides dans tous les modèles de cette logique. Plus précisément, on dit qu'une formule se déduit sémantiquement d'une théorie quand dans tout modèle de la théorie, pour toute interprétation de ses variables libres, la formule est valide. Un système de déduction est correct, fidèle ou adéquat quand toute déduction est valide sémantiquement. Il est complet quand toutes les déductions sémantiques peuvent se dériver dans le système. On parle de théorème de complétude quand il existe un système de déduction fidèle qui est complet (le système de déduction doit être raisonnable, c’est-à-dire que l'ensemble des preuves dans le système doit être récursif). Une théorie axiomatique est complète quand tout énoncé du langage de la théorie est déterminé par déduction dans la théorie : il est soit démontrable, soit de négation démontrable. Cette notion est étroitement liée à celle de théorie décidable mais ne se confond pas avec elle. Le premier théorème d'incomplétude de Gödel énonce que, sous des hypothèses raisonnables, aucune théorie arithmétique cohérente n'est complète. Il a pour conséquence qu'il n'y a pas système de déduction raisonnable qui capture entièrement la sémantique attendue, à savoir la vérité dans un modèle, celui des entiers naturels (le modèle standard de l'arithmétique). En calcul propositionnel, un système de connecteurs (de la théorie des modèles) est complet quand il permet de décrire toutes les fonctions de la sémantique. C’est-à-dire dans le cas de la logique classique (celle du calcul des prédicats qui en est une expression formelle), quand ces connecteurs (le plus souvent un jeu d’opérateurs unaires ou binaires) permettent de décrire toutes les fonctions booléennes. Dans le cas de la logique probabiliste (et de certaines de ses applications comme la logique floue), un système de connecteurs peut être aussi complet si on y adjoint des quantificateurs et des variables formelles, pour exprimer toutes les fonctions de probabilité. Toutefois la démonstration de la complétude de tels systèmes est un problème beaucoup plus difficile que celle portant sur l’ensemble des théorèmes de l’analyse mathématique portant sur les fonctions continues ou discontinues (sauf pour certaines sous-classes très limitées de fonctions de probabilités, par exemple celles pouvant s’écrire sous forme d’un développement limité ou d’une transformée dans un autre coespace dual le plus souvent lui-même non probabiliste, donc quand le système de connecteurs inclut une telle transformée). En théorie de la calculabilité ou en théorie de la complexité des algorithmes, un ensemble ou un problème de décision est complet dans une classe, si cet ensemble ou problème appartient à la classe, et si, pour une notion de réduction adéquate, tout ensemble ou problème de la classe se réduit à celui-ci. Ainsi le problème de l'arrêt, plus exactement l'ensemble des entiers n tels que la machine de code n s'arrête pour l'entrée n, est complet dans la classe des ensembles récursivement énumérables (pour la réduction récursive). La satisfaisabilité d'un ensemble de clauses du calcul propositionnel est un problème NP-complet, c’est-à-dire complet dans la classe des problèmes solubles en temps non déterministe polynomial (pour la réduction polynomiale). En théorie des ordres, un treillis est complet quand toute partie possède une borne supérieure et une borne inférieure, voir comme cas particulier les algèbres de Boole complètes. Dans le contexte de l'informatique théorique, en théorie des domaines, un ordre partiel complet (parfois abrégé cpo, de l'anglais) est un ensemble partiellement ordonné qui a un plus petit élément et dont toutes les chaînes ont une borne supérieure. En théorie des graphes, un graphe (ou un sous-graphe) non orienté est complet quand toute paire de sommets est reliée par une arête.
在数学及其相关领域中,一个对象具有完备性,即它不需要添加任何其他元素,这个对象也可称为完备的或完全的。更精确地,可以从多个不同的角度来描述这个定义,同时可以引入完备化这个概念。但是在不同的领域中,“完备”也有不同的含义,特别是在某些领域中,“完备化”的过程并不称为“完备化”,另有其他的表述,请参考代数闭域、紧化(compactification)或哥德尔不完备定理。
一个度量空间或一致空间被称为“完备的”,如果其中的任何柯西列都收敛,请参看完备空间。
在泛函分析中,一个拓扑矢量空间的子集被称为是完全的,如果的扩张在中是稠密的。如果是可分拓扑空间(separable topology space),那幺也可以导出中的任何矢量都可以被写成中元素的(有限或无限的)线性组合。更特殊地,在希尔伯特空间中(或者略一般地,在线性内积空间(inner product space)中),一组标准正交基就是一个完全而且正交的集合。
一个测度空间是完全的,如果它的任何零测集(null set)的任何子集都是可测的。请查看完全测度空间(complete measure)。
在统计学中,一个统计量(statistic)被称为完全的,如果它不允许存在0的无偏估计量(estimator)。请查看完备统计量(complete statistic)。
在图论中,一个图被称为完全的(complete graph),如果这个图是无向图,并且任何两个顶点之间都恰有一条边连接。
在范畴论,一个范畴被称为完备的,如果任何一个从小范畴到的函子都有极限。而它被称为上完备的,如果任何函子都有一个上极限。请查看范畴论中的极限定义。
在序理论和相关的领域中,如格和畴(domain theory)中,全序性(completeness)一般是指对于偏序集存在某个特定的上确界或下确界。值得特别注意的是,这个概念在特定的情况下也应用于完全布尔代数,完全格和完全偏序。并且一个有序域被称为完全的,如果它的任何在这个域中有上界的非空子集,都有一个在这个域中的最小上界;注意这个定义与序理论中的完全有界性(bounded complete)有细小的差别。在同构的意义下,有且仅有一个完全有序域,即实数。
在数理逻辑,一个理论被称为完备的,如果对于其语言中的任何一个句子,这个理论包括且仅包括或。一个系统是兼容的,如果不存在同时和非的证明。哥德尔不完备定理证明了,包含皮亚诺公理的所有公理系统都是不可能既完备又兼容的。下面还有一些逻辑中关于完备性的定义。
在证明论和相关的数理逻辑的领域中,一个形式的演算相对于一个特定的逻辑(即相对于它的语义)是完备的,如果任何由一组前提根据语义导出的陈述,都可以从这组前提出发利用这个演算语法地(syntactically)导出。形式地说,导出 。一阶逻辑在这个意义下是完备的。特别地,所有逻辑的重言式都可以被证明。即使在经典逻辑中,这与前述的完备性是不同的(即一个陈述和否定陈述对于这个逻辑而言不可能是重言式)。相反的概念被称为可靠性(soundness)。
在计算复杂度理论中,一个问题对于一个复杂度类,在某个给定类型的归约下是完全的(complete),如果在中,并且中的任何问题利用该归约都可以化归到。例如,NP完全问题在NP类和多项式时间和多对一归约的意义下是完全的。
incomplétude nom commun - féminin ( incomplétudes )