décimale是什么意思_décimale的常见用法_近义词

词典释义

n. f.
小数

常见用法
nombre décimal十进制数
système décimal十进制

短语搭配

système décimal十进制

divisions décimales十进分度

fraction décimale小数;用10的乘方做分母的分数

division décimale十进制分度

nombre décimal小数;十进制数

débordement décimal十进制溢出

chiffre décimal十进制数字

binaire décimal二-十进制转换的

numération décimale十进制命数法

deux décimales两位小数

原声例句

Le système décimal avec les Romains.

罗马人的十进制。

[innerFrench]

Ça, c'est ce qu'on appelle le système décimal.

这就是所谓的十进制。

[innerFrench]

La virgule sépare la partie entière et la partie décimale.

逗号将整数部分与小数部分分开。

[基础法语小知识]

Ah... sur le grimoire, c'est écrit en écriture décimale, pas en écriture fractionnaire.

啊… … 魔法书上是用十进制分数书写的，不是用小数写的。

[基础法语小知识]

Mais vers la fin du Moyen-Âge, c'est le système décimal qui a commencé à s'imposer.

但中世纪末，开始盛行十进制。

[innerFrench]

Les Suisses et les Belges ont été épargnés pour des raisons géographiques et ont gardé le système décimal.

瑞士人和比利时人由于地理原因幸免于此，保留了十进制的数数法。

[德法文化大不同]

Au 16e siècle, il a constaté que les commerçants avaient bien du mal à calculer avec les fractions décimales.

16世纪时，他发现商人难以用十进制分数来算账。

[基础法语小知识]

C'est grâce à Stevin de Bruges que l'écriture décimale est née et qu'on l'utilise encore aujourd'hui.

多亏了Stevin de Bruges，小数的写法得以诞生，而且我们如今还在使用这种写法。

[基础法语小知识]

Mais, ce qui est bizarre c''est qu'on a adopté le système décimal seulement à moitié, jusqu'à soixante.

但奇怪地是，我们只采纳了一半的十进制，直到60为止。

[innerFrench]

Enfin, pour être plus précis, certains Français ont adopté tout le système décimal (donc soixante, septante, huitante, nonante).

最后，补充一下，有些法国人完全采纳了十进制。

[innerFrench]

例句库

Le boulier est lié au system de numération décimale .

算盘是与十进制命数法密切相关的。

En réalité, il faut mettre une série de décimales, mais le chiffre que je donne est suffisant pour les besoins de la poésie.

英国诗人坦尼森写了一首《罪之幻影》的诗，数学家巴比奇拜读后给诗人写了如下一封信。

D'aucuns étaient partisans d'abaisser le plancher en portant le nombre de décimales des taux inclus dans le barème de trois à quatre ou en l'éliminant complètement.

一些成员主张，应将分摊比额表小数点从现在的三位数增加到四位数，以降低下限，或者干脆取消下限。

Les chiffres présentés au tableau 2 et dans tous les autres tableaux sont arrondis à une décimale près si bien que leurs totaux peuvent ne pas correspondre.

表2和所有其他表格中所列的数字均四舍五入至最近的小数，因而各项相加不一定等于总数。

Le boulier est lié au système de numération décimale : chaque boule représente, selon la tige sur laquelle elle se trouve, une unité, une dizaine, une centaine?

珠算是与制度的十进制数每个球，根据干上这是一个，十，百？

Deuxièmement, certaines décisions sur le respect visant individuellement certaines Parties et adoptées avant la dix-huitième réunion des Parties comprenaient des réductions de niveaux de consommation déterminés jusqu'à trois décimales près.

其次，某些在缔约方第十八次会议以前通过的关于各缔约方遵约情况的决定要求将消费水平的减少量具体到小数点后三位。

La réunion des Parties était convenue de revenir à la pratique consistant à communiquer les données à une décimale près (voir paragraphe 147 du rapport de la dix-huitième réunion des Parties).

缔约方会议当时同意重新采用四舍五入到小数点后一位的方法（见缔约方第十八次会议报告第147段）。

Le secrétariat avait récemment arrondi les niveaux spécifiés dans ses précédentes décisions à une décimale près avant de procéder aux vérifications concernant leur respect, mais il ne savait pas si cela correspondait effectivement aux attentes des Parties.

秘书处近期在开展遵约审查以前将这些决定中的基准量四舍五入到小数点后一位，但无法肯定结果是否符合各缔约方的期望。

Premièrement, lors de l'examen des données communiquées par les Parties à cet égard, en arrondissant à une décimale près, une Partie pourrait consommer jusqu'à 0,0499 tonne PDO de substances après la date d'élimination et toujours être considérée comme étant en situation de respect, étant donné que ce chiffre serait arrondi à zéro.

首先，在审查缔约方遵约情况的数据时，如果把数据四舍五入到小数点后一位，则缔约方可以在有关逐步淘汰期限之后消费多达0.0499耗氧潜能吨的某种物质，却仍被认为遵约，因为该数据可以四舍五入为零。

S'agissant de la troisième question, les Parties pourraient envisager d'autoriser la publication des données de consommation et de production à un plus grand nombre de décimales près, considérant que cette question différait de celles soulevées par la vérification du respect du Protocole, ou elles pourraient être invitées à fournir des indications sur d'autres critères de publication.

对于第三个问题，缔约方可以考虑允许待公布的消费量和生产量数据四舍五入到小数点后更后几位，鉴于这一问题不同于由遵约审查导致的那些问题，或者缔约方还可以就替代性公布标准提供指导。

Le secrétariat avait notamment appelé l'attention de la Somalie sur le fait que les chiffres indiqués aux paragraphes a) et b) du calendrier d'élimination avaient été arrondis à une décimale près conformément à la directive de la dix-huitième réunion des Parties et avait invité la Somalie à désigner un représentant pour participer à la quarante et unième réunion du Comité d'application afin d'assister à l'examen du plan d'action de la Partie par le Comité.

秘书处提请索马里特别注意 (a) 段和 (b) 段中的逐步淘汰时间表的数字已按照缔约方第十八次会议的指导四舍五入到小数点后一位，还邀请索马里指派一名代表参加履行委员会第四十一次会议，协助委员会审议该缔约方的行动计划。

Les principaux éléments du projet sont l'apprentissage de deux langues (langue maternelle et langue dominante), l'apprentissage de deux systèmes mathématiques (le système vicésimal maya et le système décimal occidental), l'enseignement et la mise en pratique de systèmes de valeurs complémentaires (valeurs mayas et valeurs universelles), l'enseignement de modes d'expression artistique mayas et de différentes cultures, et enfin l'identification, l'analyse et l'interprétation du monde selon la culture maya et selon les connaissances accumulées par l'humanité dans le monde entier.

这一项目的主要内容包括：教双语(母语和主要语言)；教两个系统的数学(玛雅人的二十进位系统和西方的十进位系统)；传授和检验补充价值系统(玛雅人的价值观和普遍价值观)；教授玛雅人的艺术和其它文化的艺术；最后，根据玛雅土著文化和人类共同积累的知识对世界进行探索，分析和解读。

Le secrétariat a donc demandé des avis sur ces trois questions, notamment pour savoir s'il fallait continuer à arrondir à une décimale près même après les dates d'élimination, si le fait d'arrondir à une décimale près les limites fixées par les précédentes décisions était conforme aux attentes des Parties ainsi que sur l'approche à utiliser pour diffuser et afficher les niveaux de consommation et de production calculés pour des substances à faible potentiel d'appauvrissement de la couche d'ozone, notamment les HCFC.

因此，秘书处就以下三个问题寻求指导，即是否要在逐步淘汰期限以后继续将数据四舍五入到小数点后一位，将以往决定中的基准量四舍五入到小数点后一位是否符合各缔约方的期望，以及应采用何种办法公布和显示具有低消耗臭氧潜能值的物质，特别是氟氯烃的消费和生产计算水平。

Troisièmement, arrondir à une décimale près pourrait constituer tout particulièrement un problème s'agissant de la communication des données de consommation de HCFC, étant donné que cette substance avait un faible potentiel d'appauvrissement de la couche d'ozone, allant de 0,001 à 0,52, et que la plus couramment utilisée, le HCFC-22, avait un potentiel d'appauvrissement de la couche d'ozone de 0,055. Une Partie pourrait donc consommer jusqu'à 909 kg de HCFC-22 tout en étant considérée comme ayant une consommation zéro lorsque les chiffres seraient arrondis à une décimale près.

第三，将数据四舍五入到小数点后一位可能导致在汇报氟氯烃消费量时出现一个特殊问题：由于氟氯烃具有0.001至0.52的低消耗臭氧潜能值，其中最为常用的氟氯烃-22的消耗臭氧潜能值为0.055，因此缔约方可以消费多达909千克的氟氯烃-22，并当数据被四舍五入到小数点后一位后仍将被列为处于零消费量状态。

法语百科

En mathématiques, le développement décimal est une façon d'écrire des nombres réels positifs à l'aide des puissances de 10 (négatives ou positives). Lorsque les nombres sont des entiers naturels, le développement décimal correspond à l'écriture en base 10. Lorsqu'ils sont décimaux, on obtient un développement décimal limité. Lorsqu'ils sont rationnels, on peut obtenir un développement décimal illimité périodique. Enfin, lorsqu'ils sont irrationnels, le développement décimal est illimité et non périodique.

Cas des nombres entiers

Tout nombre entier possède une écriture décimale qui nous est naturelle car enseignée depuis notre enfance. Nous prenons conscience du fait qu'il ne s'agit que d'une écriture lorsque les circonstances nous mettent en contact avec d'autres systèmes de numération.

Exemple : 123 827 = 1×10 + 2×10 + 3×10 + 8×10 + 2×10 + 7×10

Cas des nombres décimaux

Un nombre décimal est un nombre pouvant s'écrire sous la forme où N est un entier relatif et n un entier naturel.

Un nombre décimal positif possède alors un développement décimal limité comportant des puissances de 10 à exposant négatif mais le plus petit exposant ne peut être que - n.

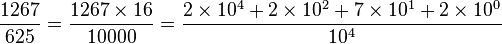
Exemple : $\frac{1267}{625} = \frac{1267 \times 16}{10000} = \frac{2 \times 10^4 + 2\times 10^2 + 7 \times 10^1 + 2\times 10^0}{10^4}$

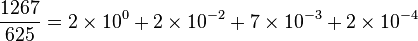
\frac{1267}{625} = 2\times 10^0 + 2\times 10^{-2} + 7\times 10^{-3} + 2\times 10^{-4}

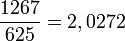
Et on vérifie très simplement à l'aide d'une calculatrice que $\frac{1267}{625} = 2,0272$

Réciproquement : tout nombre possédant un développement décimal limité est un nombre décimal car il suffit de le multiplier par la puissance de 10 adéquate pour retomber sur un entier.

Cas des nombres rationnels

Aborder l'écriture décimale de la plupart des nombres rationnels nous fait rentrer dans le monde de l'infini car l'écriture ne s'arrête jamais. On parle de développement décimal illimité.

Exemple : Division de 13 par 7

13          |7
 60         |1,85714285...
  40        |
   50       |
    10      |
     30     |
      20    |
       60   |
        40  |

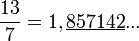Puisque l'on obtient de nouveau le reste 6 (avant dernière ligne), en abaissant le 0, on se trouvera à diviser encore 60 par 7, à réobtenir pour quotient 8, pour reste 4, etc. Le cycle 857142 s'appelle la période du développement décimal illimité périodique. On écrira $\frac{13}{7} = 1,\underline{857142}...$ Toutefois il est aussi possible de faire "ressortir" la période en plaçant une barre au-dessus de celle-ci ou plus rarement en l'encadrant entre crochets [] .

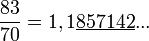La période du développement décimal ne commence pas toujours juste après la virgule : $\frac{83}{70} = 1,1\underline{857142}...$ .

On peut démontrer que tout nombre rationnel possède un développement décimal illimité périodique. Pour le comprendre, il suffit de généraliser le principe de la division précédente. Supposons que l'on divise P par Q, dans la division de P par Q, on est amené, pour les décimales après la virgule, à « abaisser des zéros ». Si le reste précédent est r, on cherche alors à diviser 10r par Q. Les restes de la division sont en nombre fini (0, 1, ..., Q - 1), donc on ne peut pas prolonger indéfiniment la division sans rencontrer deux restes identiques. Si on appelle r1 et r'1 les deux premiers restes identiques, on voit que la division de 10r1 par Q sera identique à celle de 10r'1 par Q, et donnera le même quotient q1 = q'1 et même reste r2 = r'2 et ainsi de suite.

Un nombre décimal possède aussi un développement décimal illimité de période 0.

Réciproquement, tout développement décimal illimité périodique correspond à l'écriture d'un rationnel.

Exemple : 3,25723723723... = x

100x = 325,723723723...

100x - 325 = y = 0,723723723... On peut remarquer que, si y est rationnel, x le sera aussi.

y = 0,723723....

1000y = 723,723723723...

1000y = 723 + y

999y = 723

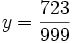y = \frac{723}{999}

. y est alors un rationnel et x aussi.

La méthode se généralise pour tout développement décimal illimité périodique. On se débarrasse de la mantisse par une multiplication par la puissance de 10 adéquate et par la soustraction d'un nombre entier. On obtient alors un nombre y s'écrivant 0,périodepériodepériode.... sur lequel on effectue le même type d'opération que plus haut : multiplication par la puissance de 10 adéquate 10y = période + y. La résolution de l'équation précédente prouve que y est rationnel et donc que x est rationnel.

Cette méthode de décalage sera employée par la suite pour calculer de façon analogue la somme des termes d'une suite géométrique.

Cas particulier de 0,99999999... = y.

En utilisant la technique précédente, on obtient 10y = 9,99999... = 9 + y. La résolution de l'équation précédente mène donc à y = 1.

1 possède donc deux « développements décimaux illimités » périodiques : 1,000000... et 0,9999.... Selon la définition d'un développement décimal illimité sur $\mathbb{R}$ , seul sera retenu le premier développement illimité, le second s'appelant un développement impropre. Il en est plus généralement de même pour tous les nombres décimaux sauf 0 : on a ainsi, par exemple, 3/5 = 0,6000000... = 0,5999999..., et là encore, seul le premier développement est retenu.

Cas des nombres réels

Si x est un nombre réel, on construit les suites de nombres décimaux suivantes :

et où E(a) désigne la partie entière de a.

u_n s'appelle l'approximation décimale de x par défaut à 10 et v_n celle par excès.

On démontre facilement que u_n et u_n+1 ne diffèrent (éventuellement) que sur la n+1 décimale qui est de 0 pour u_n et de a_n+1 pour u_n+1.

u_n s'écrit alors

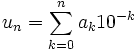
u_n = \sum_{k = 0}^{n}a_k10^{-k}

où a₀ est un entier relatif et où tous les a_k pour k = 1 à n sont des entiers compris dans {0, …, 9}.

On démontre aussi que (un) et (vn) sont des suites adjacentes encadrant x, donc elles convergent vers x. On appelle alors développement décimal illimité la suite (an) et on remarquera que

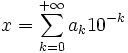x = \sum_{k = 0}^{+ \infty}a_k10^{-k}

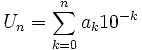Réciproquement, si (a_n) est une suite d'entiers tels que tous les a_k pour k = 1 à n sont des entiers compris dans {0, …, 9}, on démontre que la série $U_n = \sum_{k = 0}^{n}a_k10^{-k}$ est convergente dans R vers un réel $x = \sum_{k = 0}^{+ \infty}a_k10^{-k}$ . Il faut maintenant distinguer deux cas :

Si la suite (an) converge vers 9 (tous les termes égaux à 9 à partir d'un certain rang k), alors x est un décimal d'ordre k - 1. La suite (un) définie dans la première partie ne coïncidera pas à la suite (Un). La suite (an) ne sera pas appelée un DDI.

Si la suite ne converge pas vers 9, la suite (un) définie dans la première partie coïncidera à la suite (Un) . La suite (an) sera appelée un DDI.

Cette construction d'un développement illimité permet de retrouver le développement (non impropre) d'un décimal 3,5670000…, ou d'un rationnel 3,25743743743… .

On démontre que cette définition construit une bijection entre les réels et les suites (a_n) d'entiers tels que tous les a_k pour k = 1 à n sont des entiers compris dans {0, …, 9} ne convergeant pas vers 9.

Régularité dans les développements décimaux illimités

Sauf pour les décimaux et les rationnels dont le développement illimité est périodique, il n'est en général pas possible de « prévoir » les décimales d'un réel. Seuls des calculs poussés permettent de découvrir les premières décimales (on connaît jusqu'à présent les 1 241 100 000 000 premières décimales de π.)

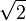Des études portant sur la fréquence des entiers dans les développements décimaux de $\sqrt{2}$ ou de π sont menées.

Lorsque la fréquence d'apparition de chaque chiffre est de 10 % dans le développement décimal, et, plus généralement, lorsque la fréquence d'apparition d'une suite de n chiffres donnée est (pour chaque suite) de 10, on dit que le réel est un nombre normal.

Curiosités

Le réel dont le développement décimal est 0,1234567891011121314151617... possède un développement décimal prévisible non périodique. Ce réel est la constante de Champernowne, du nom du mathématicien anglais qui l'a inventé en 1933. Ce nombre est évidemment irrationnel, mais aussi transcendant (prouvé par Kurt Mahler en 1961), et normal en base 10.

La constante de Copeland-Erdős 0,2357111317192329313741... constituée de la succession des nombres premiers, est elle aussi normale en base 10..

Le réel dont le développement décimal est 0,110001000000000000000001..., c'est-à-dire la somme des puissances factorielles négatives de 10 (10 + 10 + 10 + ...+ 10 + ...) possède un développement décimal prévisible non périodique. Ce réel est la constante de Liouville, du nom du mathématicien français qui l'a inventé. Ce nombre est irrationnel, mais aussi transcendant (prouvé par Joseph Liouville).

Le développement décimal est impossible dans un système positionnel sans zéro, c'est-à-dire que le développement décimal dépend non seulement d'un système de numération positionnel, mais également de l'usage du zéro positionnel.

Si on tire au hasard, uniformément, un nombre réel entre 0 et 1, les chiffres de son développement décimal forment une suite de variables aléatoires indépendantes uniformes sur Ce fait est la clé de la démonstration du théorème du nombre normal, dû à Émile Borel : à l'occasion de cette démonstration, Émile Borel a découvert le lemme de Borel-Cantelli, et a démontré la première version connue de la loi forte des grands nombres.

Développement en base quelconque

Utiliser un développement décimal fait jouer un rôle particulier à la base 10. Tout ce qui précède s'applique à n'importe quel nombre entier b (comme base), supérieur à 1. Cette fois, les nombres admettant deux développements seront ceux de la forme , les nombres rationnels restant caractérisés par la périodicité de leur développement.

En fait la base 10 présente surtout un intérêt pratique, c'est celle à laquelle nous sommes habitués. Les bases 2 et 3 notamment sont très intéressantes.

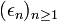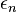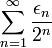Plaçons nous en base 2. L'application de $d:\{0,1\}^\N \rightarrow [0,1]$ qui associe à une suite $(\epsilon_n)_{n\ge 1}$ , où $\epsilon_n$ vaut 0 ou 1, le nombre $\sum_{n=1}^\infty\frac{\epsilon_n}{2^n}$ est surjective (car tout nombre réel admet un développement en base 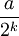2). Elle n'est pas bijective, puisque précisément les rationnels dyadiques, c’est-à-dire ceux de la forme $\frac{a}{2^k}$ , admettent deux développements.

Plaçons nous maintenant en base 3. L'application qui à la même suite associe le nombre est maintenant injective. Elle n'est pas surjective : son image est l'ensemble de Cantor. On peut tirer de cette représentation des choses curieuses, par exemple une application continue du segment sur le carré (voir ensemble de Cantor).

Articles connexes

Écriture décimale positionnelle

Entier naturel

Entier relatif

Nombre décimal

Nombre rationnel

Décimale récurrente

Nombre réel

Développement décimal de l'unité

Portail de l’arithmétique et de la théorie des nombres

中文百科

小数，是实数的一种特殊的表现形式。所有分数都可以表示成小数，小数中的圆点叫做小数点，它是一个小数的整数部分和小数部分的分界号。其中整数部分是零的小数叫做纯小数，整数部分不是零的小数叫做带小数。

2	.	718
整数部分	小数点	小数部分

性质

在小数的末尾添上或去掉任意个零，小数的大小不变。例如：0.4＝0.400，0.060＝0.06。

把小数点分别向右（或向左）移动n位，则小数的值将会扩大（或缩小）基底的n次方倍。（例如对十进位来说就是）

分类

循环小数

无限不循环小数

其他小数表示方式

现今一般表示方式：；有些地方或国家使用逗号：。

或

中文记数法

中国未引入西方的小数点前，中文有一套小数单位表示小数：分、厘、毫、丝、忽、微、纤等等，各单位是前一个的十分之一。如3.1416，读作「三又一分四厘一毫六丝」或「三个一分四厘一毫六丝」。小数点自西方传入中国后，小数单位除对译十进制词头外已逐渐不用，现时分、厘仍会用于利率。

内部链接

小数点

注解

↑ 常见于交易报价软件，小数部份以略小的字体书写，并画上底线；或中华邮政之邮票，例：常085总统府邮票；常136浆果邮票。

↑ 林鹤一、淡中济着，黄元吉译，《算术－整数及小数》，万有文库第一集，民国十八年初版。

NDL: 00572299

法法词典

décimale nom commun - féminin ( décimales )

1. mathématiques : en arithmétique nombre plus petit que un exprimé avec les chiffres compris entre zéro et neuf inclus

arrondir à trois décimales après la virgule • à la décimale près