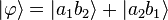La mécanique quantique est la branche de la physique qui a pour objet d'étudier et de décrire les phénomènes fondamentaux à l'œuvre dans les systèmes physiques, plus particulièrement à l'échelle atomique et subatomique.
Elle fut développée au début du XX siècle par une dizaine de physiciens américains et européens, afin de résoudre différents problèmes que la physique classique échouait à expliquer, comme le rayonnement du corps noir, l'effet photo-électrique, ou l'existence des raies spectrales.
Au cours de ce développement, la mécanique quantique se révéla être très féconde en résultats et en applications diverses. Elle permit notamment d'élucider le mystère de la structure de l'atome, et plus globalement elle s'avéra être le cadre général de description du comportement des particules élémentaires, jusqu'à constituer le socle de la physique moderne.
L'expression physique quantique désigne quant à elle un corpus théorique un peu plus étendu, qui s'appuie sur la mécanique quantique pour décrire des phénomènes particuliers, notamment les interactions fondamentales.
La mécanique quantique comporte de profondes difficultés conceptuelles, et son interprétation physique ne fait pas l'unanimité dans la communauté scientifique. Parmi ces concepts, on peut citer la dualité onde corpuscule, la superposition quantique, l'intrication quantique ou encore la non-localité.
Panorama général
Globalement, la mécanique quantique se démarque de la physique classique par deux aspects : des règles différentes quant à l'additivité des probabilités, et l'existence de grandeurs physiques ne pouvant se manifester que par multiples de quantités fixes, appelés quanta, qui donnent leur nom à la théorie.
Lois de probabilités
Dans la conception classique des lois de probabilités, lorsqu'un événement peut se produire de deux façons différentes incompatibles l'une avec l'autre, les probabilités s'additionnent. Tel n'est pas le cas en mécanique quantique, où la probabilité d'un évènement est liée à une amplitude de probabilité susceptible d'interférer, y compris de façon destructive.
Cette propriété est illustrée par l'expérience des fentes de Young, considérée notamment par Richard Feynman comme la plus emblématique du comportement quantique de la matière. Dans son cours de mécanique quantique, Feynman consacre un long chapitre à son analyse détaillée. Cette expérience illustre aussi le concept de dualité onde-corpuscule, à la base de l'interprétation standard de la théorie.
On considère actuellement qu'aux échelles macroscopiques, l'apparente non-observation de ce comportement probabiliste s'explique par un phénomène appelé décohérence. Cependant d'autres explications existent, mais aucune ne fait l'unanimité : elles relèvent essentiellement de différences dans l'interprétation de la mécanique quantique.
Existence des quanta
La mécanique quantique tire son nom de l'existence de grandeurs ne pouvant se manifester que par multiples de quantités fixes, souvent liées à la constante découverte par Max Planck. Ces grandeurs sont par exemple l'énergie ou le moment cinétique des particules.
L'illustration la plus manifeste et la plus riche en conséquences de ce phénomène se trouve probablement dans la structure de l'atome et plus précisément dans l'organisation des électrons autour du noyau. En effet, les électrons se répartissent en occupant les places laissées libres par les valeurs possibles des nombres quantiques liés à leur énergie et leur moment cinétique. Cette organisation permet d'expliquer le comportement chimique et spectroscopique des éléments naturels.
L'existence des quanta n'est pas une propriété fondamentale de la mécanique quantique, car elle peut être démontrée à partir d'autres considérations, notamment relatives à la règle sur l'additivité des probabilités mentionnée plus haut. Cependant, elle constitue certainement l'un des aspects les plus caractéristiques de la mécanique quantique, car c'est elle qui se manifeste le plus aisément dans les équations, et c'est historiquement par cet aspect que la mécanique quantique fut découverte.
Histoire
Le congrès Solvay de 1927 a réuni les meilleurs physiciens de l'époque, au nombre desquels figurent la plupart des fondateurs de la mécanique quantique.
C'est incontestablement la résolution du problème du rayonnement du corps noir qui a marqué le début de la mécanique quantique. Au début du XX siècle, Max Planck résout en effet ce problème en faisant l'hypothèse que l'énergie des atomes ne peut s'échanger que par multiples de quantités proportionnelles à la fréquence du rayonnement, selon la formule désormais célèbre :
En confrontant son modèle aux données expérimentales, il obtient alors facilement une valeur numérique précise pour la constante h, depuis appelée constante de Planck et reconnue par la suite comme l'une des trois constantes fondamentales.
Cette idée de grandeurs énergétiques ne pouvant s'échanger que de façon discrète inspirera alors de nombreux physiciens, comme Niels Bohr, qui s'en serviront notamment pour développer un modèle de la structure de l'atome. Plus généralement, ce fut le début de ce qu'on appela la théorie des quanta.
Peu de temps après la découverte de Planck, Albert Einstein, à la suite notamment de son analyse de l'effet photo-électrique, suggère que la quantité hν est l'énergie d'une particule électromagnétique qui sera plus tard appelée photon. Cette réintroduction d'une conception corpusculaire de la lumière va inciter Louis de Broglie à proposer une relation analogue à celle de Planck, mais pour la quantité de mouvement :
-
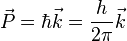
où est un vecteur d'onde. est la constante de Planck dite réduite.
Ce faisant, il est l'instigateur de la dualité onde corpuscule qui incitera certains physiciens à rechercher une description ondulatoire de la matière. Parmi ceux-ci, Erwin Schrödinger y parvient et obtient une équation différentielle, portant désormais son nom, qui permet de décrire précisément l'évolution quantique d'une particule. Cette équation prouva rapidement sa pertinence dans sa description du modèle de l'atome d'hydrogène.
Parallèlement, Werner Heisenberg avait développé une approche radicalement différente, qui s'appuyait sur des calculs matriciels directement inspirés de la mécanique analytique classique.
Ces deux approches, ainsi que la confusion concernant le concept de dualité onde corpuscule, donnaient à la mécanique quantique naissante un besoin de clarification. Cette clarification intervint grâce aux travaux d'un physicien britannique, Paul Adrien Dirac.
Dans un livre publié en 1930, intitulé Principes de la mécanique quantique, Dirac montre que les deux approches, celle de Schrödinger et Heisenberg, ne sont en fait que deux représentations d'une même algèbre linéaire. Dans cet ouvrage fondateur, Dirac extrait les lois proprement quantiques, en faisant abstraction des lois déjà imposées par la physique classique. Dirac donne alors une représentation axiomatique de la mécanique quantique, probablement inspirée des développements mathématiques de l'époque, notamment en ce qui concerne la géométrie projective.
Le travail de Dirac avait été précédé quelques années auparavant par celui réalisé par John Von Neumann, mais l'ouvrage de Von Neumann était beaucoup plus rigoureux sur le plan mathématique, de telle sorte qu'il plaisait surtout aux mathématiciens. Les physiciens lui ont préféré celui de Dirac et c'est donc essentiellement l'ouvrage de Dirac qui a laissé une postérité. Dans la préface d'une ré-édition de son livre, Von Neuman mentionne l'ouvrage de Dirac et le décrit comme « une représentation de la mécanique quantique qui peut à peine être surpassée en termes de brièveté et d'élégance », mais ajoute tout de même dans le paragraphe suivant que sa méthode « ne satisfait en aucune façon les exigences de la rigueur mathématique ».
Notions fondamentales
Paul Dirac dégage les propriétés essentiellement quantiques des phénomènes physiques et les exprime à travers quelques postulats et concepts qui sont à la base de la mécanique quantique. Elles sont présentées ici d'une façon moins formelle, plus propice à une compréhension générale. L'article détaillé présente leur formulation de façon plus rigoureuse mais aussi plus abstraite.
État quantique
En substance, un état quantique est ce qui quantifie ce que l'on peut savoir d'un système quantique. Il permet de calculer les probabilités et les valeurs moyennes mesurées des observables (position, quantité de mouvement etc.). Les états quantiques sont décrits mathématiquement par vecteur d'état dans un espace de Hilbert, représenté par une notation dédiée introduite par Dirac, dite notation bra-ket. Un état quantique s'écrit alors sous la forme . L'évolution dans le temps de ce vecteur d'état est décrit mathématiquement par la fonction d'onde , gouvernée par l'équation de Schrödinger.
Ces deux représentations concernent les états purs, c'est-à-dire les états de systèmes quantiques simples idéalisés et isolés, où chaque composante peut être quantifiée et observée. Pour les états mixtes, représentant les états quantiques en interaction complexe avec un environnement ou un appareil de mesure, où les composantes sont trop nombreuses ou inaccessibles à l'observation, l'état quantique est plutôt représenté par une matrice densité.
Dans le cas de la notation bra-ket, on exprime l'état quantique en fonction des états propres, c'est dire les états pour lesquels on est sûr que si on effectuait une mesure d'une observable, on obtiendrait à coup sûr une valeur donnée. On utilise en général pour ces états le même symbole que celui utilisé pour identifier cette valeur. Par exemple, lorsqu'on est sûr que si on effectuait cette mesure, le résultat serait une valeur , alors on note l'état . Il existe en général un certain nombre (voire une infinité) d'états propres pour une observable donnée. Par exemple, si on s'intéresse au spin d'une particule de spin 1/2, on obtient deux états propres de direction opposée : et . Pour l'observable de position, on obtient une infinité d'états propres correspondant à chacune de positions possibles ... .
Ces états propres sont des vecteurs orthogonaux de l'espace vectoriel de Hilbert, et en forment une base, liée à une observable donnée. Un état quantique quelconque est alors exprimé comme une combinaison linéaire de ces états propres, par exemple un état généralisé de spin 1/2 : , a et b étant des nombres complexes.
Deux états quantiques quelconques distincts ne sont pas forcément distinguables, car il existe une probabilité que la mesure de deux états distincts donne la même valeur mesurée. Deux états quantiques sont dits distinguables lorsqu'il existe au moins un processus de mesure dans lequel on est absolument sûr que les deux états donnent des résultats différents.
Principe de superposition
Le plus important postulat de la mécanique quantique est probablement le principe de superposition. Selon ce principe, si un système physique peut se trouver dans un état , et si de même il peut se trouver dans un état , alors il peut aussi se trouver dans un état linéairement composé :
-

où et sont deux nombres complexes quelconques.
Autrement dit, l'ensemble des états possibles d'un système physique est un espace vectoriel, dont la dimension peut être quelconque.
Le point important est qu'un état superposé n'est pas un état traduisant une ignorance vis-à-vis de l'état réel du système, mais bien une indétermination intrinsèque au système, qui n'est ni dans l'état , ni dans l'état . Ce point souleva de nombreux questionnements dans la communauté scientifique. En particulier, le principe de superposition est à l'origine de ce qu'on appelle le problème de la mesure quantique, que Schrödinger popularisa en l'appliquant à un chat qui ne serait, selon le désormais fameux paradoxe de Schrödinger, ni mort, ni vivant.
Le principe de superposition fut aussi analysé et critiqué par Einstein qui, avec Boris Podolsky et Nathan Rosen, imagina une expérience, dite expérience EPR, afin de le mettre en défaut. Une expérience comparable fut menée à la fin du XX siècle par Alain Aspect, qui confirma le principe de superposition.
Règle de Born
La règle de Born, du nom du physicien Max Born, est une interprétation probabiliste des coefficients linéaires du principe de superposition. Elle est d'ailleurs souvent appelée interprétation probabiliste.
Cette règle peut être illustrée en considérant par exemple le chat de Schrödinger, évoqué plus haut, et dont l'état quantique peut être écrit ainsi :
-
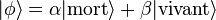
Une expérience qui chercherait à déterminer si ce chat est mort ou vif ne donnerait aucun résultat avec certitude (dans le cas contraire le chat serait soit dans l'état 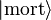 , soit dans l'état
, soit dans l'état 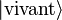 ). De façon simplifiée, il peut être dit que la règle de Born quantifie cette incertitude en stipulant que la probabilité de trouver le chat mort est égale au carré du module de
). De façon simplifiée, il peut être dit que la règle de Born quantifie cette incertitude en stipulant que la probabilité de trouver le chat mort est égale au carré du module de 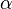 , divisé par la somme des carrés des modules de
, divisé par la somme des carrés des modules de 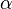 et
et 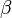 .
.
Plus généralement, pour un système dont le vecteur d'état est une combinaison linéaire d'états distinguables 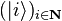 , la probabilité pour que le résultat de la mesure définissant la distinguabilité soit le même que si le système avait été dans l'état
, la probabilité pour que le résultat de la mesure définissant la distinguabilité soit le même que si le système avait été dans l'état 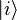 est :
est :
-
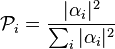 ,
,
où les 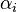 sont les coefficients linéaires du vecteur d'état.
sont les coefficients linéaires du vecteur d'état.
Pour simplifier les calculs, les vecteurs d'états sont en général normalisés afin que le dénominateur soit égal à un. Cela n'affecte en rien les calculs de probabilités. En pratique, la règle de Born s'écrit donc le plus souvent :
-
 ,
,
ou encore :
-
 , où le coefficient de proportionnalité est sous-tendu par la relation de normalisation :
, où le coefficient de proportionnalité est sous-tendu par la relation de normalisation : 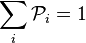 ,
,
La règle de Born est l'un des postulats de la mécanique quantique les plus difficiles à appréhender. Il fait aussi l'objet de controverses, ne serait-ce que parce que son statut axiomatique est mis en doute par au moins deux interprétations : l'interprétation des mondes multiples et l'interprétation transactionnelle. Selon ces deux interprétations, la règle de Born peut être déduite à partir de considérations mathématiques et physiques plus profondes.
Grandeur observable
Lorsque à la suite d'une expérience, on est sûr d'obtenir toujours le même résultat de mesure 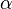 , on dit que le système physique considéré est dans l'état
, on dit que le système physique considéré est dans l'état 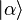 . Ceci ne signifie pas pour autant qu'on connait avec certitude le résultat d'une mesure effectuée avec un dispositif expérimental différent. En d'autres termes, la connaissance même totale de l'état d'un système ne garantit pas la connaissance parfaite de résultats de toute expérience faite sur lui.
. Ceci ne signifie pas pour autant qu'on connait avec certitude le résultat d'une mesure effectuée avec un dispositif expérimental différent. En d'autres termes, la connaissance même totale de l'état d'un système ne garantit pas la connaissance parfaite de résultats de toute expérience faite sur lui.
Ainsi par exemple, si on mesure la position d'une particule dans l'état 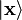 , on est sûr qu'on obtiendra
, on est sûr qu'on obtiendra 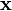 , mais par contre il n'est a priori pas possible de savoir avec certitude ce que donnera le résultat de mesure d'impulsion, car sinon la particule serait aussi dans l'état
, mais par contre il n'est a priori pas possible de savoir avec certitude ce que donnera le résultat de mesure d'impulsion, car sinon la particule serait aussi dans l'état 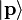 , ce qui n'est pas le cas général et constitue donc une hypothèse ad-hoc.
, ce qui n'est pas le cas général et constitue donc une hypothèse ad-hoc.
Plus généralement, si pour un certain processus de mesure A on note 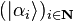 tous les états de résultat de mesure parfaitement déterminés, alors en vertu du principe de superposition, toutes les combinaisons linéaires possibles sont aussi des états possibles pour certains systèmes :
tous les états de résultat de mesure parfaitement déterminés, alors en vertu du principe de superposition, toutes les combinaisons linéaires possibles sont aussi des états possibles pour certains systèmes :
-
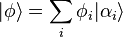
Parmi ces combinaisons linéaires, certaines peuvent très bien être des états de mesure parfaitement déterminée pour un autre processus de mesure B. La question est donc de savoir quel peut être le résultat de mesure de A pour ces états « propres » à B.
L'interprétation probabiliste des coefficients linéaires suggère alors que le résultat de mesure, s'il n'est pas déterministe, sera tout de même statistiquement égal à l'espérance mathématique :
-
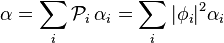
Cette expression est une forme sesquilinéaire des coefficients . Dans le sous-espace vectoriel généré par les , on peut donc écrire cette expression en utilisant un produit scalaire dans lequel la base est orthonormée. C'est le choix de ce produit scalaire qui donne un sens à la notation bra-ket : les vecteurs bra, notés « vers la gauche », sont alors les éléments de l'espace dual de l'espace des états ket. On a alors la relation :
-
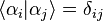
de telle sorte que l'expression de l'espérance mathématique peut s'écrire :
-
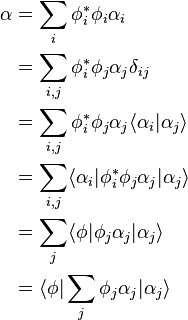
Le terme suggère l'introduction de l'opérateur linéaire dont les vecteurs propres sont les et dont les valeurs propres associées sont les , valeurs possibles des résultats de mesure. Cet opérateur est ce qu'on appelle l'observable associé au processus de mesure A. Ce n'est rien d'autre qu'un outil mathématique qui permet le calcul de l'espérance mathématique du résultat de mesure, espérance qui s'écrit alors :
-

L'intérêt d'une telle expression est qu'elle ne dépend plus explicitement de la base . On gagne ainsi en abstraction et on simplifie les calculs, un peu comme en géométrie analytique où il est souvent plus facile de manipuler les vecteurs avec leur notation abstraite plutôt qu'avec leurs coordonnées dans une base particulière.
À partir de considérations algébriques élémentaires, il est facile de se convaincre que l'observable est un opérateur auto-adjoint qui peut s'écrire en fonction de ses vecteurs propres et valeurs propres ainsi :
-
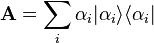
Lorsqu'on dispose de suffisamment d'observables pour décrire tout résultat de mesure, on dit qu'on dispose d'un ensemble complet d'observables qui commutent, et c'est dans l'espace hermitien généré par les vecteurs propres de ces observables que l'on travaille.
Opérateurs unitaires
Par construction, le produit scalaire dans l'espace des états permet de calculer les probabilités de résultats de mesure. Il est alors facile de comprendre que les opérateurs linéaires qui conservent ce produit scalaire jouent un rôle très important en mécanique quantique. En algèbre linéaire, ces opérateurs qui conservent le produit scalaire sont appelés opérateurs unitaires. Ils ont comme propriété essentielle d'être l'inverse de leur adjoint :
-

Cas général
Puisqu'il conserve le produit scalaire, un opérateur unitaire transforme  en un espace
en un espace 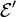 physiquement indiscernable car donnant exactement les mêmes probabilités de mesure. Inversement, s'il existe un opérateur qui transforme
physiquement indiscernable car donnant exactement les mêmes probabilités de mesure. Inversement, s'il existe un opérateur qui transforme  en un espace indiscernable, alors cet opérateur est unitaire.
en un espace indiscernable, alors cet opérateur est unitaire.
La considération de l'ensemble de tous les opérateurs unitaires sur  , ainsi que d'un sous-ensemble qui puisse être paramétré de façon continue par un scalaire μ, permet alors d'approcher
, ainsi que d'un sous-ensemble qui puisse être paramétré de façon continue par un scalaire μ, permet alors d'approcher 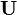 au premier ordre en μ :
au premier ordre en μ :
-
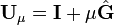
où 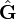 est un opérateur linéaire a priori quelconque qui peut, sans perdre en généralité, être écrit sous la forme
est un opérateur linéaire a priori quelconque qui peut, sans perdre en généralité, être écrit sous la forme 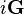 .
.
En écrivant la relation d'unitarité de 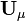 , il vient, en restant au premier ordre :
, il vient, en restant au premier ordre :
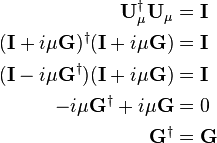
C'est-à-dire que 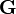 est auto-adjoint.
est auto-adjoint.
En somme, lorsqu'il existe un paramètre 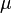 qui transforme
qui transforme  de façon continue en un espace
de façon continue en un espace  physiquement indiscernable, alors il existe un opérateur unitaire
physiquement indiscernable, alors il existe un opérateur unitaire 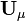 et une grandeur observable
et une grandeur observable 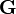 tels que
tels que 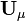 transforme
transforme  en
en  et :
et :
-
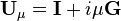
En assimilant à , et en notant le vecteur de tel que , apparait comme le taux d'accroissement de pour une variation infinitésimale de μ au voisinage de zéro, de telle sorte qu'il peut être écrit :
-
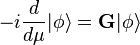
où la dépendance de  en
en 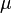 est sous-entendue (
est sous-entendue (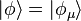 ).
).
Équation de Schrödinger
Les considérations précédentes peuvent être utilisées pour introduire l'équation de Schrödinger d'un point de vue théorique, grâce à un principe de symétrie selon lequel les lois de la physique sont invariantes dans le temps. Une autre façon de dire cela est de dire qu'une expérience menée dans un espace d'états est indiscernable d'une expérience identique menée dans un espace d'états . On peut donc appliquer les résultats précédents en prenant t (ou -t) pour :
-
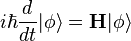
Le facteur est ici réintroduit pour satisfaire aux contraintes dimensionnelles ignorées jusqu'alors. L'expression détaillée de l'observable , appelé hamiltonien par analogie avec la mécanique classique, est le plus souvent obtenue à l'aide du principe de correspondance.
Cette formulation de l'équation de Schrödinger est assez différente de la formulation historique, et à ce titre elle est parfois appelée équation de Schrödinger généralisée et dépendante du temps.
Impulsion et moment cinétique
Comme pour l'équation de Schrödinger, mais cette fois par application du principe selon lequel les lois de la physique sont invariantes dans l'espace, on introduit l'observable du moment linéaire (aussi appelée impulsion) et ses trois composantes spatiales :
-
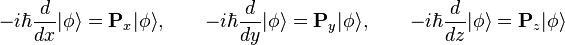
Le cas du moment cinétique (parfois appelé de façon plus explicite moment angulaire) se traite de la même façon, mais pour les rotations dans l'espace.
Commutateur
Étant donnés deux opérateurs A et B, non nécessairement observables, on définit leur commutateur ainsi :
-
![[A, B] = AB - BA](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/161b8209ebbef19abbef34c502deb03f.png)
Cet opérateur joue un rôle très important en mécanique quantique. Par exemple, lorsqu'on s'intéresse à l'évolution de l'espérance mathématique d'une observable A pour un état  :
:
-
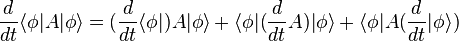
On obtient, en utilisant l'équation de Schrödinger et avec la notation 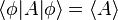 :
:
-
![\frac{d}{dt}\langle A\rangle =
\langle\frac{\partial}{\partial t}A\rangle + \frac{1}{i\hbar}\langle[A,\mathcal H]\rangle](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/dfbc49c8545a7007b0d481ffae33bd11.png)
expression qui constitue le théorème d'Ehrenfest.
Le commutateur est analogue au crochet de Poisson de la mécanique classique. Il intervient aussi dans l'explication et la description du principe d'incertitude.
Fonction d'onde
En pratique, l'état  est le plus souvent écrit dans une base
est le plus souvent écrit dans une base 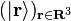 d'états de position spatiale parfaitement déterminée :
d'états de position spatiale parfaitement déterminée :
-
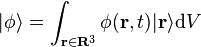
Ici l'intégration joue le rôle de la sommation utilisée plus haut notamment dans l'énoncé du principe de superposition, la différence étant qu'il s'agit d'une somme continue, c'est-à-dire de la somme d'une infinité de termes infiniment petits.
La fonction 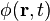 est appelée fonction d'onde et c'est sur elle que se font l'essentiel des calculs obtenus à partir de l'équation de Schrödinger.
est appelée fonction d'onde et c'est sur elle que se font l'essentiel des calculs obtenus à partir de l'équation de Schrödinger.
L'écriture de l'équation de Schrödinger non plus en fonction de  mais de la fonction d'onde se fait en remplaçant chaque terme de l'hamiltonien par les expressions correspondantes dépendant de la fonction d'onde. Par exemple, l'impulsion
mais de la fonction d'onde se fait en remplaçant chaque terme de l'hamiltonien par les expressions correspondantes dépendant de la fonction d'onde. Par exemple, l'impulsion 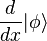 s'écrit comme vu plus haut
s'écrit comme vu plus haut 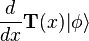 où T(x) est l'opérateur unitaire de translation de longueur x dans l'espace, c'est-à-dire tel que :
où T(x) est l'opérateur unitaire de translation de longueur x dans l'espace, c'est-à-dire tel que :
-
 .
.
Dès lors, il vient :
-
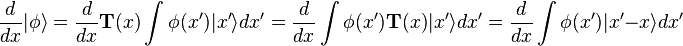
Par un changement de variable sous l'intégrale, et en se rappelant que l'équation est écrite au voisinage de x = 0, il découle :
-
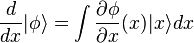
Autrement dit, l'opérateur d'impulsion agit sur le vecteur d'état en donnant un vecteur dont les coordonnées dans la représentation spatiale sont les dérivées de la fonction d'onde (à un facteur près ignoré ici). Ceci permet d'effectuer tous les calculs uniquement sur la fonction d'onde et ainsi de se ramener à la résolution d'une équation aux dérivées partielles, c'est-à-dire à l'équation de Schrödinger sous une forme plus proche de sa forme historique :
-
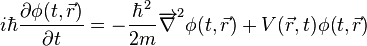
Matrice densité
La règle de Born implique que le résultat d'une expérience peut être indéterminé même lorsque l'état du système est parfaitement déterminé. Cette indétermination est intrinsèque au système, et ce en un sens qui n'a pas d'équivalent classique. Cependant, une ignorance concernant l'état exact du système peut aussi justifier une description probabiliste au sens classique du terme, c'est-à-dire avec l'acceptation usuelle des lois de probabilités.
Ainsi, dans une base orthonormale d'états 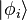 , même si l'état exact est inconnu, il est tout de même possible de lui attributer une distribution de probabilités
, même si l'état exact est inconnu, il est tout de même possible de lui attributer une distribution de probabilités 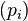 , où
, où 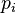 est la probabilité pour le système d'être dans l'état quantique
est la probabilité pour le système d'être dans l'état quantique 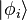 . La question est alors de savoir comment rendre compte de ce type de probabilité dans les calculs.
. La question est alors de savoir comment rendre compte de ce type de probabilité dans les calculs.
L'étude du système se réduit à celle de la mesure des observables disponibles, qui elle-même se réduit à la mesure de leur valeur moyenne qui s'écrit, pour une observable 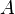 et si le système est dans l'état
et si le système est dans l'état 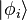 :
:
-

Comme le système est dans un état inconnu, mais avec la distribution de probabilité 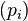 , l'espérance mathématique devient :
, l'espérance mathématique devient :
-
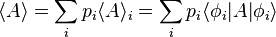
Cette expression est en quelque sorte une double espérance mathématique, prenant en compte à la fois les probabilités quantiques et classiques. Les termes  sont en effet des espérances mathématiques, pour des distributions de probabilité associées au principe de superposition et à la règle de Born. L'expression
sont en effet des espérances mathématiques, pour des distributions de probabilité associées au principe de superposition et à la règle de Born. L'expression 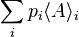 est quant à elle une espérance mathématique associée à une distribution de probabilité traduisant une ignorance vis-à-vis de l'état réel du système, c'est-à-dire une distribution de probabilité classique.
est quant à elle une espérance mathématique associée à une distribution de probabilité traduisant une ignorance vis-à-vis de l'état réel du système, c'est-à-dire une distribution de probabilité classique.
L'espérance mathématique peut alors s'écrire :
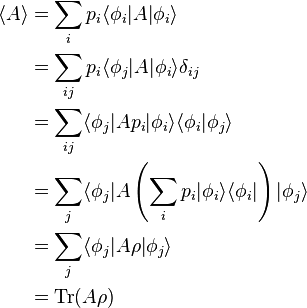
L'expression est ce qu'on appelle la matrice densité associée à la distribution de probabilités dans la base . est la trace.
La matrice densité n'est, à l'instar des observables, qu'un outil mathématique qui permet le calcul des espérances mathématiques des résultats de mesure, mais contrairement aux observables, la matrice densité incorpore la prise en compte d'une possible ignorance de l'état exact du système.
Exemples notables de problèmes quantiques
En mécanique quantique, il existe quelques problèmes et sujets d'études qui sont désormais très bien analysés, et qui s'avèrent très utiles pour la compréhension d'autres systèmes. Ils font partie intégrante du corpus théorique et sont traités en détail dans tous les manuels.
Fermions et bosons
Les lasers fonctionnent grâce à la propension qu'ont les bosons à occuper le même état quantique.
Les principes fondamentaux énoncés plus haut suffisent déjà à expliquer l'une des propriétés les plus importantes de la matière : la distinction entre bosons et fermions.
En effet, cette distinction découle essentiellement du caractère vectoriel de l'espace des états et de son interprétation probabiliste. Si on considère un système physique (ou plus simplement une particule) et que l'on note son état, alors un système physique constitué de deux de ces particules s'écrira en utilisant le produit tensoriel des deux vecteurs.
La question qui se pose alors est celle de savoir comment se comporte le système si, par la pensée, on intervertit les rôles joués par les deux particules. Autrement dit, on s'interroge sur la relation entre 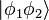 et
et 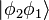 . Ces deux systèmes étant parfaitement analogues, lorsque les particules sont considérées indiscernables, elles doivent se comporter de la même façon. Leur répartition de probabilité est donc la même et elles sont donc reliées par un scalaire
. Ces deux systèmes étant parfaitement analogues, lorsque les particules sont considérées indiscernables, elles doivent se comporter de la même façon. Leur répartition de probabilité est donc la même et elles sont donc reliées par un scalaire 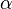 :
:
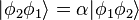
Or, si on intervertit à nouveau les particules, on doit nécessairement réobtenir le système initial, de telle sorte que :
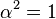
Même parmi les nombres complexes, il n'existe que deux racines carrées de l'unité : 1 et -1. Cela implique qu'il ne peut exister que deux types bien distincts de particules, celles pour lesquelles , les bosons, et celles pour lesquelles , les fermions (ces noms font référence aux physiciens qui ont découvert les statistiques associées : Satyendranath Bose et Enrico Fermi).
De cela il découle directement le principe d'exclusion de Pauli, auquel seuls les fermions obéissent. Considérons par exemple un fermion et imaginons deux particules de cette espèce dans exactement le même état .
On a : 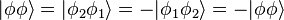 et donc :
et donc : 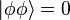
Autrement dit la probabilité pour que deux fermions soient dans le même état est toujours nulle. Une telle propriété est d'une importance considérable dans la nature. On lui doit par exemple en grande partie l'impénétrabilité des corps (en).
À l'inverse, les bosons ont tendance à se regrouper les uns avec les autres, car leurs amplitudes de probabilités interfèrent constructivement quand ils sont dans le même état. Ceci est la cause de nombreux phénomènes, comme l'émission stimulée, à la base du fonctionnement des lasers.
Des considérations comparables aux calculs effectués plus haut permettent de comprendre qu'un nombre pair de fermions se comportent comme des bosons. Ceci est la cause de phénomènes comme la supraconductivité, où les électrons forment des paires de Cooper. C'est aussi ce qui explique les différences de comportement entre les différents isotopes de l'hélium : dans un atome d'hélium 4 (He), chaque particule est présente en double (deux électrons, deux protons et deux neutrons, formant des paires de Cooper), ce qui fait de cet atome un boson. Ce qui n'est pas le cas dans l'atome d'hélium 3 (He), qui n'a qu'un neutron, ce qui fait de cet atome un fermion ; qui peut s'associer à un autre atome d'hélium 3 pour former un boson d'une paire de Cooper.
Le caractère bosonique ou fermionique des particules est lié à leur spin, par ce qu'on appelle le théorème spin-statistique.
Oscillateur harmonique
Parmi les systèmes que l'on peut résoudre analytiquement en mécanique quantique, l'un d'entre eux a une importance particulière tant sur le plan historique que théorique. Il s'agit de l'oscillateur harmonique.
En mécanique classique, l'oscillateur harmonique est un système de grande importance car il constitue une bonne approximation de n'importe quel système stable autour d'une position d'équilibre. Dans un système d'unités adéquat, l'équation énergétique s'écrit :
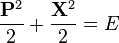
Où 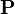 et
et  sont respectivement l'impulsion et la position du mobile.
sont respectivement l'impulsion et la position du mobile.
En mécanique quantique, l'équation est formellement la même, mais les grandeurs impliquées sont de nature différente. Au lieu d'être des scalaires réels dépendant du temps, l'impulsion et la position sont des opérateurs linéaires sur l'espace vectoriel des états. Ces grandeurs peuvent être manipulées de manière algébrique comme avec des scalaires normaux, à ceci près qu'il s'agit d'une algèbre non commutative. Il faut donc prêter attention aux commutateurs entre les opérateurs concernés. En l'occurrence, le commutateur entre et est :
![\left[\mathbf{X}, \mathbf{P}\right] = i](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/d07738709d8b57bdfe384763e6ec6b03.png)
La résolution du système passe alors par une factorisation inspirée de l'identité remarquable . En se rappelant que , on introduit donc deux opérateurs (à un facteur de normalisation près) :

Pour des raisons qui apparaissent en cours de calcul (cf article détaillé), ces opérateurs sont appelés opérateurs respectivement de création et d'annihilation de quanta, ou encore opérateurs d'échelle. Ensuite, un raisonnement par récurrence permet de montrer le caractère quantifié des niveaux d'énergie possible, et de calculer leurs valeurs. Ces quanta sont l'analogue mécanique des photons, et à ce titre ils sont parfois appelés phonons.
Cette introduction d'opérateurs de création et d'annihilation est une technique assez emblématique de la physique quantique. On la retrouve par exemple dans la théorie du moment cinétique quantique ou en théorie quantique des champs.
Particule libre
L'un des systèmes les plus simples en mécanique quantique est la particule libre, dont l'énergie est réduite à sa composante cinétique. L'équation de Schrödinger s'écrit alors :
-
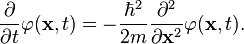
Les solutions sont de la forme :
-
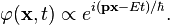
Effet tunnel
L'effet tunnel désigne la propriété que possède un objet quantique de franchir une barrière de potentiel même si son énergie est inférieure à l'énergie minimale requise pour franchir cette barrière. C'est un effet purement quantique, qui ne peut pas s'expliquer par la mécanique classique. Pour une telle particule, la fonction d'onde, dont le carré du module représente la densité de probabilité de présence, ne s'annule pas au niveau de la barrière, mais s'atténue à l'intérieur de la barrière, pratiquement exponentiellement pour une barrière assez large. Si, à la sortie de la barrière de potentiel, la particule possède une probabilité de présence non nulle, elle peut traverser cette barrière. Cette probabilité dépend des états accessibles de part et d'autre de la barrière ainsi que de l'extension spatiale de la barrière.
Spin de l'électron
Historiquement, le spin de l'électron est d'abord un phénomène expérimental observé notamment lors de l'expérience de Stern et Gerlach. En substance, il apparaît comme une sorte de très faible moment magnétique n'admettant que deux valeurs possibles, qui sont opposées et qui ne varient pas selon l'axe de mesure. Il s'agit donc d'une grandeur vectorielle ne respectant pas, du moins en apparence, les lois spatiales de la trigonométrie. Ces observations assez curieuses n'ont pu être expliquées que par la mécanique quantique.
Le spin de l'électron est donc une grandeur a priori directionnelle qui ne peut prendre que deux valeurs de magnitude égales et de sens opposées. Les états quantiques correspondant sont alors en général notés 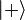 et
et 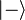 . Ces états dépendent d'un axe d'observation particulier, traditionnellement placé verticalement, c'est-à-dire selon l'axe
. Ces états dépendent d'un axe d'observation particulier, traditionnellement placé verticalement, c'est-à-dire selon l'axe 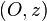 .
.
Avec un choix d'unités adéquat, cela signifie que pour un électron dans l'état 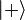 , la mesure du moment magnétique de spin selon
, la mesure du moment magnétique de spin selon 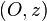 donnera à coup sûr +1 comme résultat de mesure. De la même façon un électron dans l'état
donnera à coup sûr +1 comme résultat de mesure. De la même façon un électron dans l'état 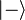 donnera nécessairement -1 comme résultat de mesure selon ce même axe.
donnera nécessairement -1 comme résultat de mesure selon ce même axe.
Dès lors, 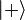 et
et 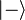 forment la base d'un espace vectoriel de dimension deux, et l'observable associée à la mesure du spin selon l'axe
forment la base d'un espace vectoriel de dimension deux, et l'observable associée à la mesure du spin selon l'axe 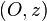 s'écrit alors, en représentation matricielle :
s'écrit alors, en représentation matricielle :
-
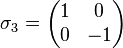
(l'indice 3 est ici choisit car l'axe 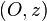 est traditionnellement le troisième axe du trièdre spatial)
est traditionnellement le troisième axe du trièdre spatial)
Par application du principe de superposition, toute superposition linéaire de 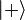 et
et 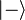 est aussi un état possible pour l'électron. Parmi ces combinaisons linéaires, il en est qui sont les vecteurs propres de deux matrices
est aussi un état possible pour l'électron. Parmi ces combinaisons linéaires, il en est qui sont les vecteurs propres de deux matrices 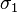 et
et 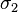 :
:
-
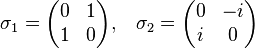
, et forment avec la matrice unité ce qu'on appelle les matrices de Pauli.
La considération d'un vecteur unitaire 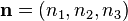 et de l'observable :
et de l'observable : 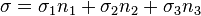 permet alors de faire apparaître la valeur moyenne suivante de
permet alors de faire apparaître la valeur moyenne suivante de 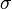 pour l'état
pour l'état 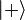 :
:
-
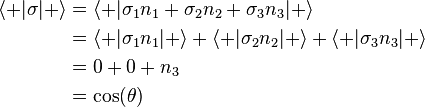
où 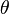 est l'angle éloignant
est l'angle éloignant 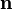 de l'axe
de l'axe 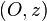 .
.
Autrement dit, dès lors que 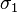 et
et 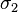 sont associés aux observables liées à la mesure du spin selon les axes
sont associés aux observables liées à la mesure du spin selon les axes 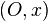 et
et 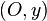 , alors les règles de trigonométries apparaissent, mais avec une signification probabiliste. C'est là un résultat typique de la mécanique quantique.
, alors les règles de trigonométries apparaissent, mais avec une signification probabiliste. C'est là un résultat typique de la mécanique quantique.
Le spin de l'électron joue un rôle très important en mécanique quantique, d'une part parce que c'est un phénomène qui n'a pas d'équivalent classique, et d'autre part parce que c'est l'un des systèmes quantiques les plus simples dans la mesure où il n'a que deux états (ou plus précisément, que son espace vectoriel est de dimension deux). À ce titre il est souvent utilisé comme modèle d'étude pour des systèmes plus complexes, même lorsque le phénomène physique sous-jacent est complètement différent. L'exemple emblématique est le modèle d'Ising.
Atome d'hydrogène
Formulation de la mécanique quantique par intégrale de chemin
Richard Feynman, dans sa thèse en 1942, introduit la notion d'intégrale de chemin afin de présenter une nouvelle formulation de la mécanique quantique. Ces résultats ne seront publiés qu'en 1948 en raison de la seconde guerre mondiale. À terme, le but de cette approche serait de formuler une théorie de l'électrodynamique quantique en développant la quantification par intégrale de chemin. Si de nos jours on retient le formalisme Hamiltonien de la mécanique quantique pour traiter des problèmes classiques (au sens non relativiste), il s'avère que la formulation de Feynman est largement prédominante pour traiter les problèmes relativistes notamment en théorie quantique des champs, l'avantage provenant du fait que cette approche est non perturbative.
Par ailleurs, en 1953, Feynman appliqua son approche pour formuler la mécanique statistique quantique (en) par intégrale de chemin (intégrale de Wiener, formule de Feynman-Kac (en)) et tenta d'expliquer la transition lambda dans l'hélium superfluide.
Mécanique quantique et relativité
La mécanique quantique est une théorie non relativiste : elle n'incorpore pas les principes de la relativité restreinte. En appliquant les règles de la quantification canonique à la relation de dispersion relativiste, on obtient l'équation de Klein-Gordon (1926). Les solutions de cette équation présentent toutefois de sérieuses difficultés d'interprétation dans le cadre d'une théorie censée décrire une seule particule : on ne peut notamment pas construire une densité de probabilité de présence partout positive, car l'équation contient une dérivée temporelle seconde. Dirac cherchera alors une autre équation relativiste du premier ordre en temps, et obtiendra l'équation de Dirac, qui décrit très bien les fermions de spin un-demi comme l'électron.
La théorie quantique des champs permet d'interpréter toutes les équations quantiques relativistes sans difficulté.
L'équation de Dirac incorpore naturellement l'invariance de Lorentz avec la mécanique quantique, ainsi que l'interaction avec le champ électromagnétique mais qui est traité encore de façon classique (on parle d'approximation semi-classique). Elle constitue la mécanique quantique relativiste. Mais du fait précisément de cette interaction entre les particules et le champ, il est alors nécessaire, afin d'obtenir une description cohérente de l'ensemble, d'appliquer la procédure de quantification également au champ électromagnétique. Le résultat de cette procédure est l'électrodynamique quantique dans laquelle l'unité entre champ et particule est encore plus transparente puisque désormais la matière elle aussi est décrite par un champ. L'électrodynamique quantique est un exemple particulier de théorie quantique des champs.
D'autres théories quantique des champs ont été développées par la suite au fur et à mesure que les autres interactions fondamentales ont été découvertes (théorie électrofaible, puis chromodynamique quantique).
Les inégalités de Heisenberg
Les relations d'incertitude de Heisenberg traduisent l'impossibilité de préparer un état quantique correspondant à des valeurs précises de certains couples de grandeurs conjuguées. Ceci est lié au fait que les opérateurs quantiques associés à ces grandeurs classiques ne commutent pas.
Les inégalités de Heisenberg sont très fréquemment désignées par l'expression « principe d'incertitude ». Stricto sensu, cette appellation est trompeuse : ces inégalités ne sont pas un principe car elles sont parfaitement démontrées grâce à l'analyse de Fourier, et elles ne concernent pas des incertitudes au sens commun du terme mais une indétermination intrinsèque, propre à la nature aléatoire de la mécanique quantique.
Inégalité position-impulsion
Considérons par exemple la position 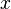 et l'impulsion
et l'impulsion 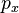 d'une particule. En utilisant les règles de la quantification canonique, il est facile de vérifier que les opérateurs de position et d'impulsion vérifient :
d'une particule. En utilisant les règles de la quantification canonique, il est facile de vérifier que les opérateurs de position et d'impulsion vérifient :
-
![\left[ \hat{x}^i , \hat{p}_j \right] f( \vec{r} ) \ = \ \left( \hat{x}^i \hat{p}_j - \hat{p}_j \hat{x}^i \right) f( \vec{r} ) \ = \ i \hbar \ \delta^i_j \ f( \vec{r} )](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/62362cb0af883942cfabebfe7554c591.png)
La relation d'incertitude est définie à partir des écarts quadratiques moyens de grandeurs conjuguées. Dans le cas de la position et de l'impulsion d'une particule, elle s'écrit par exemple :
-
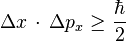
Plus l'état possède une distribution resserrée sur la position, plus sa distribution sur les valeurs de l'impulsion qui lui est associée est large. Cette propriété rappelle le cas des ondes, via un résultat de la transformée de Fourier, et exprime ici la dualité onde-corpuscule. Il est clair que ceci mène à une remise en cause de la notion classique de trajectoire comme chemin continu différentiable.
Inégalité temps-énergie
Il existe également une relation d'incertitude portant sur l'énergie d'une particule et la variable temps. Ainsi, la durée 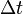 nécessaire à la détection d'une particule d'énergie
nécessaire à la détection d'une particule d'énergie 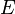 à
à 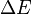 près vérifie la relation :
près vérifie la relation :
-
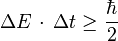
Cependant, la dérivation de cette inégalité énergie-temps est assez différente de celle des inégalités position-impulsion.
En effet, si le hamiltonien est bien le générateur des translations dans le temps en mécanique hamiltonienne, indiquant que temps et énergie sont conjuguées, il n'existe pas d'opérateur temps en mécanique quantique (« théorème » de Pauli), c'est-à-dire qu'on ne peut pas construire d'opérateur qui obéirait à une relation de commutation canonique avec l'opérateur hamiltonien :
-
![\left[ \hat{H} , \hat{T} \right] \ = \ i \hbar \ \hat{1}](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/3a765ef8f1a765c0c92401c2bf39d3f8.png)
ceci pour une raison très fondamentale : la mécanique quantique a en effet été inventée pour que chaque système physique stable possède un état fondamental d'énergie minimum. L'argument de Pauli est le suivant : si l'opérateur temps existait, il posséderait un spectre continu. Or, l'opérateur temps, obéissant à la relation de commutation canonique, serait aussi le générateur des translations en énergie. Ceci entraîne alors que l'opérateur hamiltonien posséderait lui aussi un spectre continu, en contradiction avec le fait que l'énergie de tout système physique stable se doit d'être bornée inférieurement.
Intrication
La notion d'intrication quantique intervient dès lors que deux systèmes 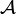 et
et 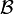 sont considérés dans leur ensemble comme formant un seul et unique système
sont considérés dans leur ensemble comme formant un seul et unique système 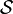 . Cette assertion peut être vérifiée par exemple dans le cas simple où les espaces d'état de
. Cette assertion peut être vérifiée par exemple dans le cas simple où les espaces d'état de 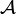 et
et 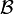 ont pour bases les vecteurs propres
ont pour bases les vecteurs propres  et
et 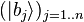 de deux observables
de deux observables 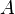 et
et 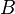 agissant respectivement sur
agissant respectivement sur 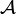 et
et 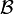 .
.
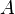 et
et 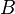 agissent nécessairement aussi sur
agissent nécessairement aussi sur 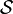 puisque
puisque 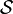 est constitué de la réunion de
est constitué de la réunion de 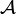 et
et 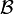 . On peut donc noter
. On peut donc noter 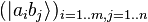 le vecteur d'état de
le vecteur d'état de 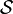 tel que dans cet état la mesure de
tel que dans cet état la mesure de 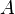 donne à coup sûr
donne à coup sûr 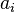 et la mesure de
et la mesure de 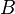 donne à coup sûr
donne à coup sûr 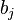 .
.
D'après le principe de superposition, toutes les combinaisons linéaires des vecteurs d'état 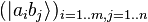 sont des états possibles du système. Or, il existe
sont des états possibles du système. Or, il existe 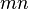 tels vecteurs, et donc l'espace vectoriel qu'ils engendrent est au moins de dimension
tels vecteurs, et donc l'espace vectoriel qu'ils engendrent est au moins de dimension 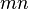 . Dans le cas général, cette dimension est supérieure à
. Dans le cas général, cette dimension est supérieure à 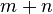 , c'est-à-dire au nombre de degrés de libertés nécessaires pour décrire les systèmes
, c'est-à-dire au nombre de degrés de libertés nécessaires pour décrire les systèmes 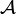 et
et 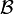 considérés séparément.
considérés séparément.
Il apparaît donc que dans le cas général la description complète des deux systèmes dans leur ensemble ne peut être réduite à celle des deux systèmes pris séparément. Autrement dit, il existe des états de 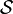 tels qu'il n'existe aucun état de
tels qu'il n'existe aucun état de 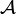 ni aucun état de
ni aucun état de 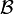 , c'est-à-dire aucune combinaison linéaire des
, c'est-à-dire aucune combinaison linéaire des  ni aucune combinaison linéaire des
ni aucune combinaison linéaire des 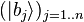 qui permettent d'obtenir les probabilités de résultats de mesure. De tels états de
qui permettent d'obtenir les probabilités de résultats de mesure. De tels états de 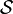 sont alors dit intriqués. Un tel exemple d'état intriqué est :
sont alors dit intriqués. Un tel exemple d'état intriqué est :
-
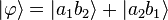
Deux systèmes ou deux particules peuvent être intriqués dès qu'il existe une interaction entre eux. En conséquence, les états intriqués sont la règle plutôt que l'exception. Une mesure effectuée sur l'une des particules changera son état quantique selon le postulat quantique de la mesure. Du fait de l'intrication, cette mesure aura un effet instantané sur l'état de l'autre particule, même si la ligne d'univers qui relie les deux évènements « mesure 1 » et « mesure 2 » de l'espace-temps est une courbe de genre espace ! Par suite, le fait que la mécanique quantique tolère l'existence d'états intriqués, états ayant effectivement été observés en laboratoire et dont le comportement est en accord avec celui prévu par la mécanique quantique (voir l'expérience d'Aspect), implique que la mécanique quantique est une théorie physique non locale. Néanmoins, il est incorrect d'assimiler ce changement d'état à une transmission d'information plus rapide que la vitesse de la lumière (et donc une violation de la théorie de la relativité). La raison est que le résultat de la mesure relatif à la première particule est toujours aléatoire, dans le cas des états intriqués comme dans le cas des états non intriqués. Il est donc impossible de « transmettre » quelque information que ce soit, puisque la modification de l'état de l'autre particule, pour immédiate qu'elle soit, conduit à un résultat de la mesure relatif à la seconde particule qui est toujours aussi aléatoire que celui relatif à la première particule. Les corrélations entre les mesures des deux particules, bien que très réelles et mises en évidence dans de nombreux laboratoires de par le monde, resteront indétectables tant que les résultats des mesures ne seront pas comparés, ce qui implique nécessairement un échange d'information classique, respectueux de la Relativité (voir aussi le Paradoxe EPR).
La téléportation quantique fait usage de l'intrication pour assurer le transfert de l'état quantique d'un système physique vers un autre système physique. Ce processus est le seul moyen connu de transférer parfaitement l'information quantique. Il ne peut dépasser la vitesse de la lumière et est également « désincarné », en ce sens qu'il n'y a pas de transfert de matière (contrairement à la téléportation fictive de Star Trek).
Cet état ne doit pas être confondu avec l'état de superposition. Un même objet quantique peut avoir deux (ou plus) états superposés. Par exemple un même photon peut être dans l'état « polarité longitudinale » et « polarité transversale » simultanément. Le chat de Schrödinger est simultanément dans l'état « mort » et « vivant ». Un photon qui passe une lame semi-réfléchissante est dans l'état superposé « photon transmis » et « photon réfléchi ». C'est uniquement lors de l'acte de mesure que l'objet quantique possédera un état déterminé.
Dans le formalisme de la physique quantique, un état d'intrication de plusieurs objets quantiques est représenté par un produit tensoriel des vecteurs d'état de chaque objet quantique. Un état de superposition ne concerne qu'un seul objet quantique (qui peut être une intrication), et est représenté par une combinaison linéaire des différentes possibilités d'états de celui-ci.
Téléportation quantique
On ne peut déterminer l'état d'un système quantique qu'en l'observant, ce qui a pour effet de détruire l'état en question. Celui-ci peut en revanche, une fois connu, être en principe recréé ailleurs. En d'autres termes, la duplication n'est pas possible dans le monde quantique, seule l'est une reconstruction en un autre endroit, voisine du concept de téléportation dans la science-fiction.
Élaborée théoriquement en 1993 par C.H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, et W. Wootters dans l'article Teleporting an unknown quantum state by dual classical and EPR channels, de la Physical Review Letter, cette reconstruction a été réalisée expérimentalement en 1997, sur des photons, par l'équipe d'Anton Zeilinger à Innsbruck, et plus récemment sur des atomes d'hydrogène.
Paradoxes
Ces « paradoxes » nous questionnent sur l'interprétation de la mécanique quantique, et révèlent dans certains cas à quel point notre intuition peut se révéler trompeuse dans ce domaine qui ne relève pas directement de l'expérience quotidienne de nos sens.
Chat de Schrödinger
Ce paradoxe (1935) met en évidence les problèmes d'interprétation du postulat de réduction du paquet d'onde.
Paradoxe EPR et expérience d'Alain Aspect
Ce paradoxe (1935) met en évidence la non-localité de la physique quantique, impliquée par les états intriqués.
Expérience de Marlan Scully
Cette expérience peut être interprétée comme une démonstration que les résultats d'une expérience enregistrée à un instant T dépendent objectivement d'une action effectuée à un temps ultérieur T+t. Selon cette interprétation, la non-localité des états intriqués ne serait pas seulement spatiale, mais également temporelle.
Toutefois, la causalité n'est pas strictement violée car il n'est pas possible — pour des raisons fondamentales — de mettre en évidence, avant l'instant T+t, que l'état enregistré à l'instant T dépend d'un évènement ultérieur. Ce phénomène ne peut donc donner aucune information sur l'avenir.
Contrafactualité
Selon la mécanique quantique, des évènements qui auraient pu se produire, mais qui ne se sont pas produits influent sur les résultats de l'expérience.
La décohérence : du monde quantique au monde classique
Alors que les principes de la mécanique quantique s'appliquent a priori à tous les objets contenus dans l'univers (nous y compris), pourquoi continuons-nous à percevoir classiquement l'essentiel du monde macroscopique ? En particulier, pourquoi les superpositions quantiques ne sont-elles pas observables dans le monde macroscopique ? La théorie de la décohérence explique leurs disparitions très rapides en raison du couplage inévitable entre le système quantique considéré et son environnement.
Cette théorie a reçu une confirmation expérimentale avec les études portant sur des systèmes mésoscopiques pour lesquels le temps de décohérence n'est pas trop court pour rester mesurable, par exemple un système de quelques photons dans une cavité (Haroche et al., 1996)

 词典释义:
词典释义:
 】量子
】量子

 , 电磁
, 电磁
 ;
;
 ;
; 宙
宙 ;
; 宙
宙 ,
, 宙论;
宙论; ;
; ;
;
 ;
; ;
;
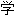
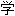
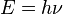
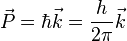

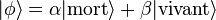
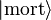 , soit dans l'état
, soit dans l'état 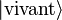 ). De façon simplifiée, il peut être dit que la règle de Born quantifie cette incertitude en stipulant que la probabilité de trouver le chat mort est égale au carré du module de
). De façon simplifiée, il peut être dit que la règle de Born quantifie cette incertitude en stipulant que la probabilité de trouver le chat mort est égale au carré du module de 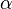 , divisé par la somme des carrés des modules de
, divisé par la somme des carrés des modules de 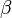 .
.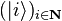 , la probabilité pour que le résultat de la mesure définissant la distinguabilité soit le même que si le système avait été dans l'état
, la probabilité pour que le résultat de la mesure définissant la distinguabilité soit le même que si le système avait été dans l'état 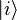 est
est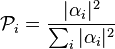 ,
,
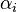 sont les coefficients linéaires du vecteur d'état.
sont les coefficients linéaires du vecteur d'état. ,
,
 , où le coefficient de proportionnalité est sous-tendu par la relation de normalisation
, où le coefficient de proportionnalité est sous-tendu par la relation de normalisation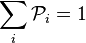 ,
,
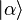 . Ceci ne signifie pas pour autant qu'on connait avec certitude le résultat d'une mesure effectuée avec un dispositif expérimental différent. En d'autres termes, la connaissance même totale de l'état d'un système ne garantit pas la connaissance parfaite de résultats de toute expérience faite sur lui.
. Ceci ne signifie pas pour autant qu'on connait avec certitude le résultat d'une mesure effectuée avec un dispositif expérimental différent. En d'autres termes, la connaissance même totale de l'état d'un système ne garantit pas la connaissance parfaite de résultats de toute expérience faite sur lui.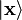 , on est sûr qu'on obtiendra
, on est sûr qu'on obtiendra 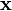 , mais par contre il n'est a priori pas possible de savoir avec certitude ce que donnera le résultat de mesure d'impulsion, car sinon la particule serait aussi dans l'état
, mais par contre il n'est a priori pas possible de savoir avec certitude ce que donnera le résultat de mesure d'impulsion, car sinon la particule serait aussi dans l'état 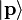 , ce qui n'est pas le cas général et constitue donc une hypothèse ad-hoc.
, ce qui n'est pas le cas général et constitue donc une hypothèse ad-hoc.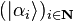 tous les états de résultat de mesure parfaitement déterminés, alors en vertu du principe de superposition, toutes les combinaisons linéaires possibles sont aussi des états possibles pour certains systèmes
tous les états de résultat de mesure parfaitement déterminés, alors en vertu du principe de superposition, toutes les combinaisons linéaires possibles sont aussi des états possibles pour certains systèmes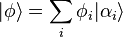
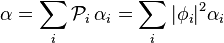
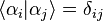
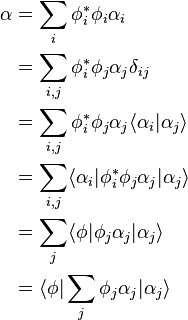

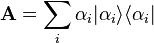

 en un espace
en un espace 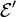 physiquement indiscernable car donnant exactement les mêmes probabilités de mesure. Inversement, s'il existe un opérateur qui transforme
physiquement indiscernable car donnant exactement les mêmes probabilités de mesure. Inversement, s'il existe un opérateur qui transforme 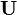 au premier ordre en μ
au premier ordre en μ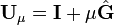
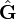 est un opérateur linéaire a priori quelconque qui peut, sans perdre en généralité, être écrit sous la forme
est un opérateur linéaire a priori quelconque qui peut, sans perdre en généralité, être écrit sous la forme 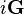 .
.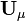 , il vient, en restant au premier ordre
, il vient, en restant au premier ordre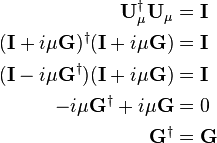
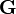 est auto-adjoint.
est auto-adjoint.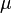 qui transforme
qui transforme  physiquement indiscernable, alors il existe un opérateur unitaire
physiquement indiscernable, alors il existe un opérateur unitaire 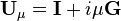
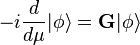
 en
en 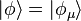 ).
).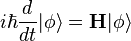
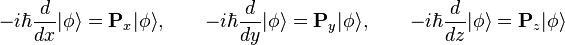
![[A, B] = AB - BA](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/161b8209ebbef19abbef34c502deb03f.png)
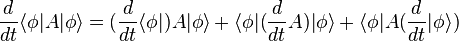
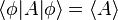
![\frac{d}{dt}\langle A\rangle =
\langle\frac{\partial}{\partial t}A\rangle + \frac{1}{i\hbar}\langle[A,\mathcal H]\rangle](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/dfbc49c8545a7007b0d481ffae33bd11.png)
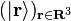 d'états de position spatiale parfaitement déterminée
d'états de position spatiale parfaitement déterminée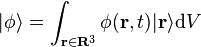
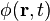 est appelée fonction d'onde et c'est sur elle que se font l'essentiel des calculs obtenus à partir de l'équation de Schrödinger.
est appelée fonction d'onde et c'est sur elle que se font l'essentiel des calculs obtenus à partir de l'équation de Schrödinger.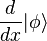 s'écrit comme vu plus haut
s'écrit comme vu plus haut 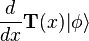 où T(x) est l'opérateur unitaire de translation de longueur x dans l'espace, c'est-à-dire tel que
où T(x) est l'opérateur unitaire de translation de longueur x dans l'espace, c'est-à-dire tel que .
.
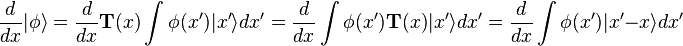
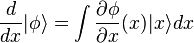
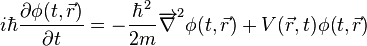
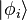 , même si l'état exact est inconnu, il est tout de même possible de lui attributer une distribution de probabilités
, même si l'état exact est inconnu, il est tout de même possible de lui attributer une distribution de probabilités 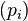 , où
, où 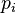 est la probabilité pour le système d'être dans l'état quantique
est la probabilité pour le système d'être dans l'état quantique 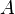 et si le système est dans l'état
et si le système est dans l'état 
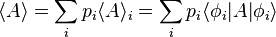
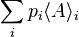 est quant à elle une espérance mathématique associée à une distribution de probabilité traduisant une ignorance vis-à-vis de l'état réel du système, c'est-à-dire une distribution de probabilité classique.
est quant à elle une espérance mathématique associée à une distribution de probabilité traduisant une ignorance vis-à-vis de l'état réel du système, c'est-à-dire une distribution de probabilité classique.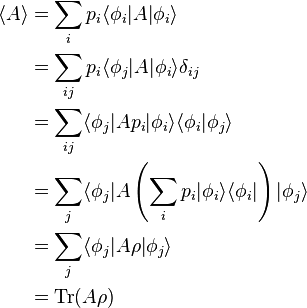
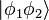 et
et 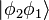 . Ces deux systèmes étant parfaitement analogues, lorsque les particules sont considérées indiscernables, elles doivent se comporter de la même façon. Leur répartition de probabilité est donc la même et elles sont donc reliées par un scalaire
. Ces deux systèmes étant parfaitement analogues, lorsque les particules sont considérées indiscernables, elles doivent se comporter de la même façon. Leur répartition de probabilité est donc la même et elles sont donc reliées par un scalaire 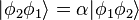
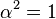
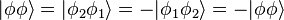 et donc
et donc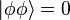
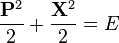
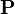 et
et  sont respectivement l'impulsion et la position du mobile.
sont respectivement l'impulsion et la position du mobile.![\left[\mathbf{X}, \mathbf{P}\right] = i](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/d07738709d8b57bdfe384763e6ec6b03.png)

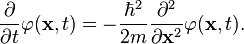
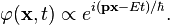
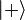 et
et 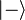 . Ces états dépendent d'un axe d'observation particulier, traditionnellement placé verticalement, c'est-à-dire selon l'axe
. Ces états dépendent d'un axe d'observation particulier, traditionnellement placé verticalement, c'est-à-dire selon l'axe 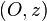 .
.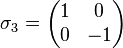
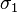 et
et 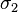
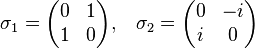
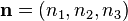 et de l'observable
et de l'observable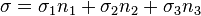 permet alors de faire apparaître la valeur moyenne suivante de
permet alors de faire apparaître la valeur moyenne suivante de 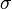 pour l'état
pour l'état 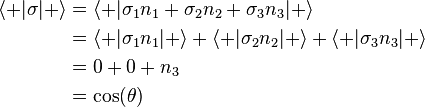
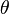 est l'angle éloignant
est l'angle éloignant 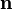 de l'axe
de l'axe 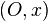 et
et 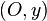 , alors les règles de trigonométries apparaissent, mais avec une signification probabiliste. C'est là un résultat typique de la mécanique quantique.
, alors les règles de trigonométries apparaissent, mais avec une signification probabiliste. C'est là un résultat typique de la mécanique quantique.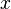 et l'impulsion
et l'impulsion 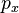 d'une particule. En utilisant les règles de la quantification canonique, il est facile de vérifier que les opérateurs de position et d'impulsion vérifient
d'une particule. En utilisant les règles de la quantification canonique, il est facile de vérifier que les opérateurs de position et d'impulsion vérifient![\left[ \hat{x}^i , \hat{p}_j \right] f( \vec{r} ) \ = \ \left( \hat{x}^i \hat{p}_j - \hat{p}_j \hat{x}^i \right) f( \vec{r} ) \ = \ i \hbar \ \delta^i_j \ f( \vec{r} )](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/62362cb0af883942cfabebfe7554c591.png)
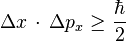
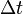 nécessaire à la détection d'une particule d'énergie
nécessaire à la détection d'une particule d'énergie 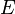 à
à 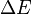 près vérifie la relation
près vérifie la relation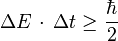
![\left[ \hat{H} , \hat{T} \right] \ = \ i \hbar \ \hat{1}](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/3a765ef8f1a765c0c92401c2bf39d3f8.png)
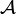 et
et 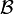 sont considérés dans leur ensemble comme formant un seul et unique système
sont considérés dans leur ensemble comme formant un seul et unique système 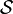 . Cette assertion peut être vérifiée par exemple dans le cas simple où les espaces d'état de
. Cette assertion peut être vérifiée par exemple dans le cas simple où les espaces d'état de  et
et 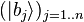 de deux observables
de deux observables 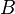 agissant respectivement sur
agissant respectivement sur 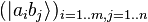 le vecteur d'état de
le vecteur d'état de 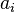 et la mesure de
et la mesure de 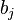 .
.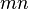 tels vecteurs, et donc l'espace vectoriel qu'ils engendrent est au moins de dimension
tels vecteurs, et donc l'espace vectoriel qu'ils engendrent est au moins de dimension 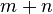 , c'est-à-dire au nombre de degrés de libertés nécessaires pour décrire les systèmes
, c'est-à-dire au nombre de degrés de libertés nécessaires pour décrire les systèmes