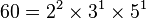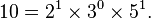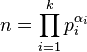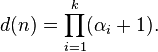Les diviseurs de 10 représentés à l'aide de réglettes Cuisenaire: 1, 2, 5 et 10
En arithmétique, un diviseur d'un entier n est un entier qui, multiplié par un autre entier judicieusement choisi, donne n. Plus formellement, si d et n sont deux entiers, d est un diviseur de n seulement s'il existe un entier k tel que dk = n. Ainsi 2 est un diviseur de 10 car 2 × 5 = 10.
La notion de diviseur est liée à celle de multiple, car si d divise n alors n est un multiple de d, et à la notion de divisibilité.
Le nom vient de l'opération arithmétique de division : si a, b sont des entiers avec b non nul, et si c = a/b est un entier, alors a est le dividende, b le diviseur et c le quotient.
Ensemble des diviseurs d'un entier
Si l'entier n est nul, tout entier divise n.
Si l'entier n est non nul, il possède des diviseurs positifs et négatifs, mais pas de diviseur nul. Si d est un diviseur de n alors –d est aussi un diviseur de n. Ces observations expliquent pourquoi on ne s’intéresse souvent qu'aux diviseurs positifs d'un entier positif. Par la suite, on se placera dans cette situation.
Diagramme de Hasse des diviseurs de 60 : une arête entre deux sommets indique que l'élément le plus bas est un diviseur de l'élément le plus haut.
Ainsi l'ensemble des diviseurs (positifs) de 10 est {1, 2, 5, 10} et celui de 60 est {1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60}.
Si d est un diviseur de n, tout diviseur de d est aussi un diviseur de n. Cette propriété induit une sorte de hiérarchie parmi les diviseurs d'un entier qui peut être visualisée sous forme d'un diagramme de Hasse.
Si n est égal à 1, n ne possède qu'un seul diviseur : 1.
Tout entier n strictement supérieur à 1 possède au moins deux diviseurs 1 et n qui sont appelés ses diviseurs triviaux. Un diviseur de n différent de n est un diviseur strict de n (ou partie aliquote — le terme diviseur propre est utilisé comme synonyme tantôt de diviseur strict, tantôt de diviseur non trivial). Un entier n qui possède exactement deux diviseurs est appelé un nombre premier. Un nombre premier diviseur de n est appelé un diviseur premier de n.
Le théorème fondamental de l'arithmétique énonce que tout entier strictement supérieur à 1 s'écrit de manière unique sous forme d'un produit de puissances de nombres premiers qui sont ses diviseurs premiers. Cette décomposition en facteurs premiers permet d'énumérer tous les diviseurs de l'entier. Si où les pi sont des nombres premiers distincts et les αi des exposants entiers strictement positifs, alors, d est un diviseur de n si et seulement si il existe des entiers βi compris au sens large entre 0 et αi tels que
Ainsi la décomposition de 60 est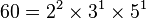 
et 10 est un diviseur de 60 car il peut s'écrire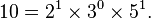 
Fonctions liées à l'ensemble des diviseurs
Il existe des fonctions d'un entier n créées à partir de l'ensemble de ses diviseurs. Les plus classiques sont les fonctions « nombre de diviseurs » et « somme des diviseurs ».
La fonction « nombre de diviseurs » donne le nombre d(n) des diviseurs de n. Ainsi d(10) = 4, d(36) = 9 et d(60) = 12. La décomposition en facteurs premiers de n permet de donner une valeur explicite à cette fonction. Si la décomposition de n est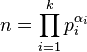 
alors 
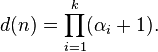
Les fonctions « somme des diviseurs » et « somme des diviseurs stricts » interviennent dans l'étude des nombres parfaits, nombres abondants, nombres déficients ou nombres amiables, ainsi que dans les suites aliquotes.
Elles font partie de la grande famille des fonctions diviseur.
Diviseur dans un anneau
La définition de diviseur se généralise à un anneau commutatif : si a et b sont deux éléments d'un anneau A, b divise a si et seulement si il existe un élément c de A tel que a = bc.
Une attention spéciale doit être portée sur la notion de diviseur de zéro. Selon la définition précédente, tout élément de A divise 0A (élément neutre de l'addition dans l'anneau A) car a × 0A = 0A. Cependant, dans un anneau non intègre, il existe des éléments de A, non nuls, b et c tels que bc = 0A. Ces éléments sont appelés des diviseurs de zéro dans A.
Note et référence
↑ Aviva Szpirglas, Algèbre L3 : Cours complet avec 400 tests et exercices corrigés [détail de l’édition], partie IV, chap.9, I.5, p. 462.
词典释义：
学】除
;因
, 因子
, 公因子
度仪, 
度头
度头
压器
裂
, 离间
, 
母;
离器;
，
开，划
;
;
;