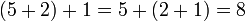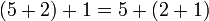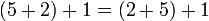En mathématiques, et plus précisément en algèbre générale, une loi de composition interne ou loi interne sur un ensemble S est dite associative si pour tous x, y et z dans S, .

Des exemples de lois associatives incluent les lois d'addition et de multiplication des nombres réels, des nombres complexes et des matrices carrées, l'addition des vecteurs, et l'intersection, la réunion d'ensembles. Aussi, si M est un ensemble quelconque et S désigne l'ensemble de toutes les fonctions de M vers M, alors l'opération de composition des fonctions sur S est associative. Un exemple de loi non associative est donné par le produit vectoriel sur un espace euclidien orienté de dimension 3. Un autre est la soustraction des nombres réels.

En effet :

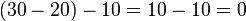
et

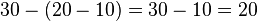
donc,

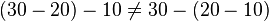
Un ensemble muni d'une loi interne associative et unifère est appelé un monoïde.

在数学中，结合律是二元运算可以有的一个性质，意指在一个包含有二个以上的可结合运算子的表达式，只要算子的位置没有改变，其运算的顺序就不会对运算出来的值有影响。亦即，重新排列表达式中的括号并不会改变其值。例如：

上式中的括号虽然重新排列了，但表达式的值依然不变。当这在任何实数的加法上都成立时，我们说「实数的加法是一个可结合的运算」。

结合律不应该和交换律相混淆。交换律会改变表达式中算子的位置，而结合律则不会。例如：

是一个结合律的例子，因为其中的括号改变了（且因此运算子在运算中的顺序也改变了），而算子5、2、1则在原来的位置中。再来，

则不是一个结合律的例子，因为算子2和5的位置互换了。

可结合的运算在数学中是很常见的，且事实上，大多数的代数结构确实会需要它们的二元运算是可结合的。不过，也有许多重要且有趣的运算是不可结合的；其中一个简单的例子为矢量积。

定义

形式上，一个在集合S上的二元运算被称之为可结合的若其满足下面的结合律： 。 运算的顺序并不会影响到表达式的值，且可证明这在含有「任意」多个运算的表达式之下也依然是成立的。因此，当是可结合的时，运算的顺序可以不需要去规范而不会使其意义不清，所以可以省略掉括号而简单写成： 不过，需要记住的是，改变运算的顺序并不包含或允许以移动表达式中的算子来改变其真实的运算。

例子

在算术中，实数的加法和乘法都是可结合的，即：

复数和四元数的加法与乘法是可结合的。八元数的加法也是可结合的，但其乘法则是不可结合的。

最大公因数和最小公倍数的运算都是可结合的。

因为线性变换是个可表示成矩阵的函数，其中的函数复合则可以用矩阵乘法来表示，立即可知矩阵乘法为可结合的。

集合的交集和联集为可结合的：

若M是某个集合且S为所有从M映射至M的函数所组成的集合，则在S上的函数复合的运算是可结合的：

更一般性地，给定四个集合M、N、P和Q，且h: M → N, g: N → P、f: P → Q，则

给定一个有三个元素A、B和C的集合，其运算如下：

不可结合性

(0.1+0.2)+0.3

0.1+(0.2+0.3)