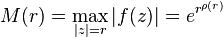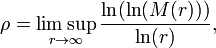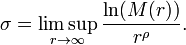La fonction associant à chaque nombre réel sa partie entière est traitée à l'article Partie entière. Voir aussi la page Entier.
En analyse complexe, une fonction entière est une fonction holomorphe définie sur tout le plan complexe. C'est le cas notamment de la fonction exponentielle complexe, des fonctions polynômes et de leurs combinaisons par composition, somme et produit, telles que sinus, cosinus et les fonctions hyperboliques.
Le quotient de deux fonctions entières est une fonction méromorphe.
Considérée comme un cas particulier de la théorie des fonctions analytiques, la théorie élémentaire des fonctions entières ne fait que tirer les conséquences de la théorie générale. C'est celle que l'on voit essentiellement dans un premier cours sur la théorie des fonctions complexes (souvent enrichi du théorème de factorisation de Weierstrass). Mais l'étude, commencée depuis le milieu du XIX siècle, par Cauchy, Laguerre, Weierstrass... s'est considérablement enrichie sous l'impulsion de Borel, Hadamard, Montel, Valiron, Blumenthal... (sans oublier Nevanlinna) et constitue maintenant une imposante théorie.
La théorie des fonctions entières se fixe comme buts de classifier les fonctions entières selon leurs croissances, de préciser le lien entre les coefficients de Taylor de la fonction et la croissance, le lien entre les zéros éventuels et le comportement de la fonction, et les relations entre la fonction et ses dérivées sur ces questions.
Ces aspects de la théorie des fonctions entières ont été étendus aux fonctions méromorphes.
Les fonctions entières dans la théorie des fonctions analytiques
On classe habituellement les fonctions analytiques complexes selon leur complexité, et cette complexité est celle de leurs singularités. Hormis les fonctions polynômes, apparaissent ainsi les fonctions entières qui sont l'objet de cet article, les fonctions méromorphes qui sont des quotients de fonctions entières et dont les seules singularités sont polaires, les fonctions présentant des singularités essentielles ou des points de branchement formant ainsi les fonctions les plus compliquées parmi les fonctions analytiques d'une seule variable complexe.
Les fonctions entières apparaissent comme des généralisations des fonctions polynômes : elles se comportent comme des "polynômes de degré infini". Ce sont ainsi les fonctions analytiques les plus simples en dehors des polynômes, n'ayant aucune singularité à distance finie et une seule singularité à l'infini, comme on le verra. Cependant l'étude de ces fonctions est difficile et il reste encore de très nombreuses questions ouvertes bien que cette étude soit commencée depuis près de deux cents ans.
Théorie élémentaire
Soit f une fonction analytique complexe holomorphe en z. Elle est développable en série entière autour du point z selon la formule de Taylor-MacLaurin
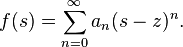
La théorie des séries entières montre que la série précédente converge absolument et uniformément dans le disque ouvert de centre z et de rayon R donné par le théorème de Cauchy-Hadamard :
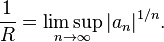
Le principal résultat de la théorie des fonctions analytiques complexes est que le rayon de convergence est déterminé par la distance 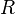 entre le point
entre le point 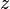 et la singularité la plus proche.
et la singularité la plus proche.
On dit d'une fonction analytique complexe qu'elle est entière lorsqu'elle est holomorphe en tout point du plan complexe. Elle n'a donc pas de singularité à distance finie.
Rappelons qu'une fonction holomorphe en un point y est indéfiniment dérivable.
Soit f une fonction entière. Comme toute fonction analytique holomorphe en un point, elle est développable en série entière convergente de la forme
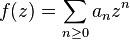
et, comme elle n'a d'autre singularité que le point à l'infini, le rayon de convergence est infini. Autrement dit, la série converge quelle que soit la valeur de z.
On a donc
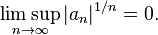
Et il en est de même de chacune de ses dérivées qui sont entières également.
La formule intégrale de Cauchy
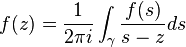
permet, en développant la fraction 1/(s-z) en série entière, d'identifier les coefficients de Taylor à des intégrales :
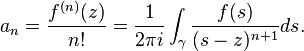
Dans les deux cas est un chemin fermé (un lacet) sans boucle entourant z.
Les inégalités de Cauchy
Dans la formule intégrale donnant les coefficients, en appelant le maximum du module de la fonction sur le disque de centre z et de rayon R, une majoration simple donne les inestimables inégalités de Cauchy
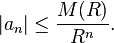
Le théorème de Liouville
Un résultat important sur les fonctions entières est le théorème de Liouville:
Théorème de Liouville — Si une fonction entière est bornée, alors elle est constante.
Une démonstration possible est l'application des inégalités de Cauchy en remarquant que 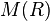 est alors borné quel que soit
est alors borné quel que soit 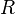 . Il suffit donc de faire tendre
. Il suffit donc de faire tendre 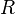 vers l'infini pour avoir le résultat.
vers l'infini pour avoir le résultat.
Cela peut être utilisé pour fournir une démonstration élégante, par l'absurde, du théorème de d'Alembert-Gauss :
Théorème de d'Alembert-Gauss — Tout polynôme de degré n admet exactement n racines complexes comptées avec leur multiplicité.
Le petit théorème de Picard renforce considérablement le théorème de Liouville
Petit théorème de Picard — Toute fonction entière non constante prend, sur le plan complexe, toutes les valeurs sauf une au plus.
Dans un certain sens, qui sera précisé plus tard, la théorie des fonctions entières tourne entièrement autour du petit théorème de Picard.
Propriétés algébriques
Une fonction holomorphe définie sur un domaine – c'est-à-dire un ouvert connexe – s'étend en une fonction entière si et seulement si le rayon de convergence de sa série de Taylor est infini en un point quelconque de son domaine.
L'ensemble des fonctions entières est stable par composition et forme une sous-algèbre complexe de l'espace des fonctions continues du plan complexe dans lui-même.
Le point à l'infini
Comme une fonction entière est constante si elle est bornée, et qu'elle ne peut avoir aucun autre point singulier que l'infini, le point à l'infini est un point singulier pour toute fonction entière non constante. Il ne peut s'agir que d'un pôle ou d'une singularité essentielle. Dans le premier cas (le pôle à l'infini), la fonction entière est un polynôme. Dans le second cas (singularité essentielle en l'infini), on dit que la fonction est transcendante.
Le principe des zéros isolés
Soit f une fonction analytique dans un domaine U, s'annulant en a. Alors, ou f est identiquement nulle, ou il existe un disque D de centre a, pour lequel f(s) est non nul, quel que soit s dans D autre que a.
Ceci se déduit du principe du prolongement analytique.
Le théorème de l'image ouverte
Si f est une fonction analytique non constante sur un ouvert U, alors f(U) est un ouvert.
On peut le démontrer à partir du principe des zéros isolés.
Le principe du maximum
Soit f une fonction analytique non constante sur un domaine D. Du théorème de l'image ouverte on déduit immédiatement :
le module de f ne possède pas de maximum local dans D (donc, si D est borné, le maximum de |f| se trouve sur la frontière de D) ;
si f ne s'annule pas sur D alors |f| ne possède pas non plus de minimum local dans D ;
la partie réelle de f ne possède dans D ni maximum local, ni minimum local.
On en déduit notamment le lemme de Schwarz.
Plus généralement, toute fonction sous-harmonique (comme |f| et, si f ne s'annule pas, 1/|f|) vérifie le principe du maximum, donc toute fonction harmonique (comme Re(f)) vérifie le principe du maximum et du minimum.
Les théorèmes de Phragmén-Lindelöf
Le principe de Phragmén-Lindelöf (en) est une généralisation du principe du module maximum à des domaines non bornés.
La croissance des fonctions entières
Le module maximum des fonctions entières
On dit d'une fonction analytique complexe qu'elle est entière lorsqu'elle est définie sur le plan complexe tout entier et holomorphe en chaque point. Elle ne présente donc que le point à l'infini pour seule singularité.
On pose
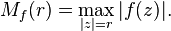
Cette fonction croît monotonement, par suite du principe du maximum. Et, en corollaire du théorème de Liouville, elle n'est pas bornée pour les fonctions entières non constantes.
Elle est appelée module maximum de la fonction 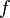 .
.
La fonction ln 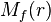 est une fonction convexe de ln r. (Hadamard)
est une fonction convexe de ln r. (Hadamard)
La fonction ln 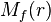 est continue et analytique par intervalles. (Blumenthal)
est continue et analytique par intervalles. (Blumenthal)
En conséquence de la convexité, ln 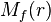 admet une dérivée à droite et à gauche, et ces dérivées sont croissantes. Il existe une fonction
admet une dérivée à droite et à gauche, et ces dérivées sont croissantes. Il existe une fonction 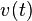 croissante (mais pas nécessairement continue) telle que
croissante (mais pas nécessairement continue) telle que
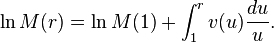
L'ordre des fonctions entières
Si pour une valeur quelconque 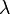 , on a
, on a
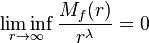
la fonction f est un polynôme de degré au plus égal à 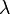 .
.
Lorsque l'égalité précédente n'a lieu pour aucune valeur de 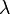 , on compare la croissance de
, on compare la croissance de 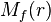 à
à 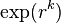 . Si l'on a, à partir d'une valeur
. Si l'on a, à partir d'une valeur 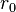 de
de  , l'inégalité
, l'inégalité
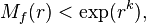
on dit que la fonction est d'ordre fini. L'ordre (supérieur) de croissance de 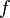 est donné par la formule
est donné par la formule
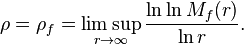
On distingue, parmi les fonctions entières de même ordre 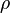 , les fonctions de type
, les fonctions de type 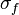 défini par la formule
défini par la formule
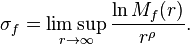
Selon la valeur de 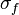 , on distingue le type minimal (
, on distingue le type minimal (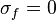 ), normal (
), normal (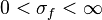 ) ou maximal (
) ou maximal ( ).
).
On montre les résultats suivants :
Exemples
La fonction 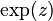 est d'ordre 1 ainsi que les fonctions
est d'ordre 1 ainsi que les fonctions 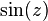 et
et 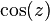 .
.
La fonction de Mittag-Leffler
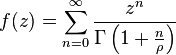
est d'ordre 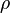 .
.
Il en est de même de la fonction de Lindelöf définie par
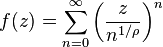
Relation entre les coefficients et la croissance
Si la fonction entière est telle que
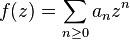
et que
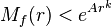
pour  suffisamment grand,
suffisamment grand,
alors on a
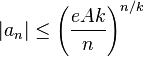
pour 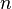 suffisamment grand.
suffisamment grand.
Réciproquement, si l'on a
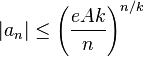
pour 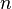 suffisamment grand, alors, pour tout
suffisamment grand, alors, pour tout 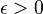 ,
,
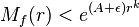
pour  suffisamment grand.
suffisamment grand.
De ce résultat on déduit
L'ordre de la fonction entière est déterminé par la formule
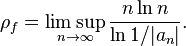
Le type de la fonction entière est déterminé par la formule
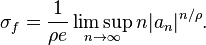
Le lemme de Borel-Carathéodory
On a vu que le maximum sur un cercle est en rapport avec les coefficients de la fonction développée en série entière. On peut se demander s'il en est de même, par exemple, avec seulement la partie réelle de la fonction. Ce lien est fourni de manière générale par le lemme de Borel-Carathéodory, qui donne de plus une estimation concernant les dérivées :
Soit f(z) une fonction analytique dans la boule fermée B(0,R) de centre 0 et de rayon R, et A(r) le maximum de sa partie réelle prise sur le cercle de rayon r.
Alors on a l'inégalité suivante, pour tout r compris dans ]0,R[:
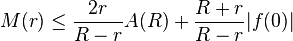
et, si 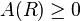
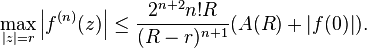
L'ordre de la dérivée d'une fonction entière
La dérivée d'une fonction entière est obtenue par dérivation formelle de sa série entière. En appliquant la formule de Cauchy-Hadamard, on voit que la dérivée d'une fonction entière est elle-même entière. La question de l'ordre de la dérivée se pose donc naturellement. Le calcul de l'ordre par la formule précédemment donnée montre que
L'ordre de la dérivée d'une fonction entière est égal à l'ordre de cette fonction.
Et, comme une fonction entière est indéfiniment dérivable, il en est de même de toutes ses dérivées.
Ordre inférieur et ordre précisé L
Pour comparer plus finement la croissance des fonctions entières, on est amené à regarder l'ordre inférieur de croissance, défini par la quantité
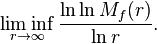
On montre que
L'ordre inférieur de la dérivée d'une fonction entière est égal à l'ordre inférieur de cette fonction.
Mais cela ne suffit pas. On montre l'existence, pour une fonction entière 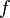 d'ordre fini
d'ordre fini 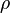 , d'une fonction
, d'une fonction 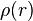 ayant les propriétés suivantes :
ayant les propriétés suivantes :
est définie et continue, dérivable à droite et à gauche en chaque point.
On a ainsi défini un ordre précisé L de 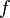 .
.
Les fonctions entières à croissance régulière
Dans ses études sur les fonctions entières, Émile Borel a défini les fonctions entières à croissance régulière en supposant que l'ordre de la fonction entière est
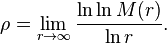
Il résulte de la définition que les ordres supérieur et inférieur sont égaux. C'est en ce sens que la fonction est à croissance régulière.
Une condition nécessaire et suffisante pour qu'une fonction entière d'ordre 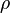 soit une fonction à croissance régulière est
soit une fonction à croissance régulière est
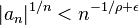
pour tout entier 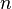 assez grand et tout
assez grand et tout 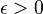 et qu'il existe une suite d'entiers
et qu'il existe une suite d'entiers 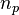 telle que
telle que
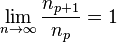
et pour laquelle on a
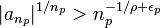
avec
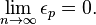
Factorisation des fonctions entières d'ordre fini
Le théorème de factorisation de Weierstrass
Cette importante propriété de factorisation (et sa généralisation par Hadamard) : fait l'objet d'un article à part entière : théorème de factorisation de Weierstrass.
Estimations sur le produit canonique
Le théorème de Boutroux-Cartan énonce un résultat fréquemment utilisé dans les recherches sur les fonctions entières. Le problème est d'estimer le produit 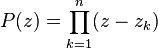 en dehors du voisinage des zéros. On suppose que l'on connaît
en dehors du voisinage des zéros. On suppose que l'on connaît 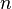 .
.
Le terme maximum de la série de Taylor
Soit 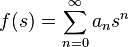 une fonction entière. La série
une fonction entière. La série 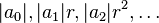 est une série décroissante à partir d'un certain rang et tendant vers 0, quel que soit
est une série décroissante à partir d'un certain rang et tendant vers 0, quel que soit  . Il y a donc, pour chaque
. Il y a donc, pour chaque  un terme supérieur ou égal à tous les autres. Soit
un terme supérieur ou égal à tous les autres. Soit 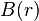 la valeur de ce terme et soit
la valeur de ce terme et soit 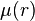 le rang (le plus grand, s'ils sont plusieurs) de ce terme.
le rang (le plus grand, s'ils sont plusieurs) de ce terme. 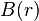 est une fonction croissante de
est une fonction croissante de  qui tend vers l'infini. D'après l'inégalité de Cauchy, on a
qui tend vers l'infini. D'après l'inégalité de Cauchy, on a 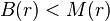 .
.
Le rang 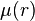 est une fonction non-décroissante de
est une fonction non-décroissante de  qui tend vers l'infini avec
qui tend vers l'infini avec  .
.
Entre les fonctions 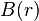 ,
, 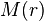 et
et 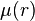 existe une double inégalité:
existe une double inégalité:
![B(r) < M(r) < B(r)\left[2\mu\left(r+ \frac{r}{\mu(r)}\right)+1\right]](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/2868115584202f7f78432a9791aa8064.png)
et de cette double inégalité on déduit
Pour une fonction d'ordre fini, les fonctions 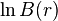 et
et 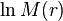 sont asymptotiquement égales.
sont asymptotiquement égales.
On en déduit ensuite une relation sur 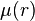 :
:
Pour une fonction entière parfaitement régulière d'ordre fini 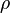 et d'ordre précisé
et d'ordre précisé 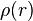 , on a
, on a 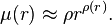
De manière générale, on a la formule
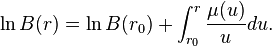
La distribution des valeurs des fonctions entières
Soit une fonction 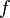 de la variable complexe définie par la série
de la variable complexe définie par la série
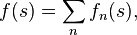 la série des modules étant convergente. Si R est une région du plan complexe où la variation de l'argument de
la série des modules étant convergente. Si R est une région du plan complexe où la variation de l'argument de 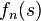 est inférieure à
est inférieure à 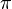 lorsque
lorsque 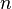 varie, la fonction
varie, la fonction 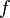 ne peut s'annuler qu'en dehors de cette région.
ne peut s'annuler qu'en dehors de cette région.
Les zéros des fonctions entières
Par suite du théorème fondamental de l'algèbre, un polynôme de degré n admet n racines dans 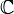 . Donc, plus un polynôme admet de zéros, plus il croît rapidement.
. Donc, plus un polynôme admet de zéros, plus il croît rapidement.
Ceci est aussi le cas des fonctions entières mais d'une manière plus complexe. La relation entre la croissance des fonctions entières et la répartition de ses zéros constitue l'un des thèmes principaux de la théorie de ces fonctions.
La formule de Jensen et l'exposant de convergence des zéros
Cette formule est fondamentale dans la suite de la théorie, même si elle n'intervient pas explicitement. On la démontre par exemple par l'emploi de la formule de Green.
On a, pour une fonction ayant des zéros aux points 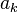 , ne présentant aucun pôle dans le disque
, ne présentant aucun pôle dans le disque 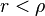 et en posant
et en posant 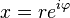
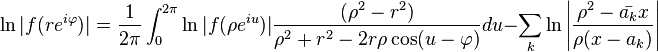
Cette formule est la formule de Poisson-Jensen.
On en déduit la formule de Jensen:
Soit f une fonction analytique dans le disque 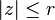 contenant les zéros
contenant les zéros 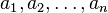 . Alors
. Alors
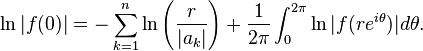
Cette formule permet de lier le nombre des zéros à la croissance de la fonction. Soit 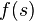 une fonction entière ayant tous ses zéros
une fonction entière ayant tous ses zéros 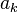 dans le disque de rayon
dans le disque de rayon  . On appelle
. On appelle 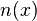 le nombre de zéros de modules inférieurs ou égaux à
le nombre de zéros de modules inférieurs ou égaux à 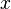 .
.
On a alors
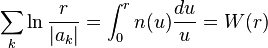
et ainsi, pour une fonction non nulle en 0, on trouve la forme suivante de la formule de Jensen:
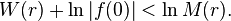
Pour une fonction entière d'ordre 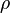 fini, on voit que
fini, on voit que 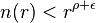 .
.
On en déduit que la série
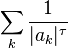
est convergente pour 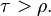
On appelle ainsi ordre réel (Borel) ou exposant de convergence de la suite des zéros la valeur de 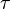 la plus petite pour laquelle la série converge. On en déduit donc ce théorème de Borel :
la plus petite pour laquelle la série converge. On en déduit donc ce théorème de Borel :
L'exposant de convergence de la suite des zéros est au plus égal à l'ordre.
Le genre
On dit que la fonction entière f est de genre p, d'après Laguerre, lorsque l'on peut la mettre sous la forme 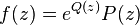 ou
ou 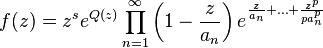 sans que cette décomposition puisse se faire pour p-1, où Q est un polynôme de degré p au plus, P, un polynôme quelconque et le produit infini le produit de Weierstrass.
sans que cette décomposition puisse se faire pour p-1, où Q est un polynôme de degré p au plus, P, un polynôme quelconque et le produit infini le produit de Weierstrass.
Le plus petit entier qui majore l'exposant de convergence est aussi le genre de la fonction.
Le genre se détermine par la formule de Laguerre :
Une fonction entière 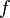 est de genre
est de genre 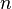 si et seulement si
si et seulement si 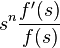 tend vers 0 uniformément quand
tend vers 0 uniformément quand 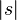 tend vers l'infini.
tend vers l'infini.
On ne saurait être trop prudent avec la notion de genre. Lindelöf a montré que la fonction
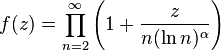
où 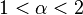 est d'ordre 1, et de genre 0 mais
est d'ordre 1, et de genre 0 mais 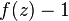 est de genre 1. De même
est de genre 1. De même 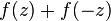 est de genre 1 mais
est de genre 1 mais 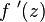 est de genre 0.
est de genre 0.
Valiron a montré cependant le théorème suivant :
Si f est une fonction de genre n, les fonctions f-a sont de genre n également sauf pour une valeur de a au plus.
Un théorème de Laguerre
Dans ses investigations sur les fonctions entières à la suite du mémoire fondateur de Weierstrass, Laguerre démontra que
Si une fonction entière f admet des zéros tous réels, il en est de même de sa dérivée pourvu que le genre de f soit égal à 0 ou à 1.
Le lien entre la croissance et la distribution des zéros
Le résultat le plus profond est le petit théorème de Picard qu'on énonce ainsi
Toute fonction entière prend toutes les valeurs complexes sauf une au plus.
La valeur non prise éventuelle est appelée valeur exceptionnelle de Picard.
Soit une fonction d'ordre fini 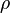 , d'ordre précisé L
, d'ordre précisé L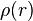 et
et 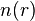 le nombre des zéros de module inférieur ou égal à
le nombre des zéros de module inférieur ou égal à  . On a l'inégalité
. On a l'inégalité
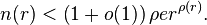
Les fonctions entières d'ordre non-entier
Dans le cas des fonctions entières d'ordre non entier, celles-ci n'admettent aucune valeur exceptionnelle au sens du théorème de Picard. Ces fonctions ont donc une infinité de solutions à l'équation 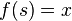 , quelle que soit la valeur de
, quelle que soit la valeur de 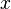 et en particulier
et en particulier
Toute fonction entière d'ordre non entier admet une infinité de zéros.
Les fonctions entières d'ordre entier
Si l'ordre est entier, le cas d'exception du théorème de Picard est possible. Dans ce cas, on a la précision suivante apportée par Émile Borel :
Le nombre 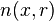 des racines de l'équation
des racines de l'équation 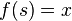 de module inférieur à
de module inférieur à  ne peut être d'un ordre de grandeur inférieur à
ne peut être d'un ordre de grandeur inférieur à 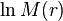 que pour une seule valeur de
que pour une seule valeur de 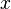 au plus.
au plus.
On montre qu'il existe des fonctions entières d'ordre entier n'ayant qu'un nombre fini de zéros et qui ne se réduisent pas à un polynôme. Mais cela ne peut être le cas des fonctions entières paires dont l'ordre est un entier impair.
Les fonctions entières et les angles
Une fonction entière d'ordre 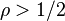 est d'ordre
est d'ordre 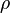 dans tout angle de mesure supérieure à
dans tout angle de mesure supérieure à 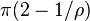 .
.
Les cercles de remplissage
Le mathématicien français Milloux, dans sa thèse soutenue en 1924, a défini des cercles particuliers, appelés par lui cercles de remplissages et dont le rayon augmente indéfiniment, dans lesquels la fonction entière prend toutes les valeurs en dessous d'un nombre A(r) tendant vers l'infini avec r sauf peut-être dans un cercle dont le rayon tend vers 0 avec 1/r. Il a démontré le résultat suivant :
Dans la couronne circulaire d'épaisseur , dont la circonférence médiane est la circonférence , on a l'inégalité
Il existe au moins un cercle C(r), appelé cercle de remplissage, dont le centre est sur le circonférence et de rayon dans lequel la fonction f(z) prend toutes les valeurs inférieures en module à A(r), sauf peut-être dans un voisinage d'une valeur a(r), ce voisinage étant inclus dans le cercle de centre a(r) et de rayon 2/A(r).
Les cercles de remplissage sont utiles pour préciser les solutions de l'équation f(z)=a.
Les valeurs asymptotiques
On peut se demander si une fonction entière non constante peut, dans certaines régions, avoir une valeur asymptotique finie ou si elles ont toujours une limite finie. On sait qu'elles ne peuvent pas avoir de valeurs asymptotiques finies dans toutes les directions par suite du théorème de Liouville. On dit que f admet la valeur asymptotique a s'il existe un chemin, appelé chemin de détermination a pour lequel f(s) tend vers a quand s tend vers l'infini en restant sur le chemin.
Donc pour toute fonction entière non constante, il existe au moins un chemin de détermination 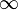 .
.
Pour une fonction d'ordre inférieur à 1/2, il existe une infinité de cercles de centre l'origine et de rayon indéfiniment croissant sur lesquels le module minimum tend vers l'infini. Il n'existe donc pas de valeur asymptotique finie pour les fonctions entières d'ordre inférieur à 1/2. En fait, Wiman a montré le théorème suivant :
Pour une fonction 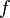 d'ordre
d'ordre 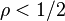 et d'ordre précisé L
et d'ordre précisé L 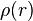 , on a, pour tout
, on a, pour tout 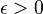 , l'inégalité
, l'inégalité
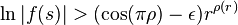
sur une infinité de cercles de rayons tendant vers l'infini.
On a donc sur ces cercles
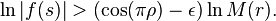
Supposons maintenant qu'une fonction entière possède deux chemins de déterminations a et b. Alors, dans le domaine défini entre les deux chemins de détermination soit il existe un chemin de détermination 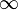 , soit les valeurs a et b sont égales et tout chemin vers l'infini inclus entre les deux chemins de détermination est un chemin de détermination a (=b).
, soit les valeurs a et b sont égales et tout chemin vers l'infini inclus entre les deux chemins de détermination est un chemin de détermination a (=b).
La conjecture de Denjoy
Il a été conjecturé par Denjoy qu'une fonction entière d'ordre fini a au plus valeurs asymptotiques. Cette conjecture est devenue le théorème de Ahlfors (en).
Il ne peut ainsi y avoir qu'au plus 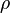 lignes droites allant de 0 à l'infini et menant à des valeurs asymptotiques différentes. De ce fait, l'angle entre deux telles lignes est au moins
lignes droites allant de 0 à l'infini et menant à des valeurs asymptotiques différentes. De ce fait, l'angle entre deux telles lignes est au moins 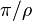 .
.
La fonction indicatrice de Phragmén-Lindelöf
La définition de l'ordre 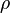 d'une fonction entière d'ordre fini et les théorèmes de Phragmén-Lindelöf suggèrent l'intérêt qu'il y aurait à étudier la fonction
d'une fonction entière d'ordre fini et les théorèmes de Phragmén-Lindelöf suggèrent l'intérêt qu'il y aurait à étudier la fonction
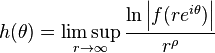
en fonction de ![\theta \in [-\pi,\pi]](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/87349317c914d3839f7ad62d8091edab.png) puisque la croissance sur une demi-ligne se répercute sur les lignes voisines.
puisque la croissance sur une demi-ligne se répercute sur les lignes voisines.
Par définition, 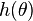 est l'indicatrice de de Phragmén-Lindelöf. C'est une fonction périodique de période
est l'indicatrice de de Phragmén-Lindelöf. C'est une fonction périodique de période 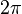 qui peut prendre des valeurs réelles, mais peut être
qui peut prendre des valeurs réelles, mais peut être 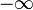 ou
ou 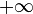 .
.
On a alors :
Soit f une fonction entière d'ordre 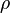 et d'indicatrice
et d'indicatrice 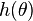 . Si h est finie dans l'intervalle [a,b] alors, quel que soit
. Si h est finie dans l'intervalle [a,b] alors, quel que soit 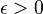 , il existe
, il existe 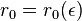 tel que pour tout
tel que pour tout 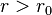 , on ait
, on ait
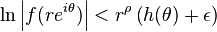
uniformément dans tout sous-intervalle de ]a,b[.
dont on déduit :
Sous les conditions du théorème précédent, tout sous-intervalle dans lequel 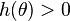 est de longueur supérieure à
est de longueur supérieure à 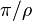 . Tout sous-intervalle dans lequel
. Tout sous-intervalle dans lequel 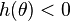 est de longueur inférieure ou égale à
est de longueur inférieure ou égale à 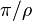 . De plus tout sous-intervalle où
. De plus tout sous-intervalle où 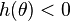 est suivi d'un point où
est suivi d'un point où 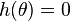 et d'un intervalle où
et d'un intervalle où 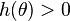 .
.
Le théorème de Carlson
On peut se demander s'il existe des conditions assurant qu'une fonction entière soit définie de manière unique par les valeurs qu'elle prend sur un ensemble dénombrable. Posé de cette manière, sans restriction sur l'ensemble, il semble que la réponse soit négative a priori. En fait, il n'en est rien et dans ce genre de question, le résultat de Carlson est à l'origine de tout un pan de recherche. On peut l'exprimer de la manière suivante :
Soit f une fonction entière d'ordre 1 et de type 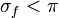 . La fonction f est entièrement déterminée par les valeurs f(n), pour n=1, 2, … De plus, si le type est strictement inférieur à ln 2, alors
. La fonction f est entièrement déterminée par les valeurs f(n), pour n=1, 2, … De plus, si le type est strictement inférieur à ln 2, alors
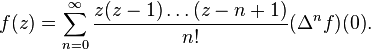
Sa démonstration utilise l'indicatrice de Phragmén-Lindelöf.
Le théorème de Pólya
Les valeurs entières prises sur un ensemble par une fonction entière imposent des restrictions sur sa croissance. Pólya, en 1915, a par exemple démontré le théorème suivant
Soit 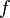 une fonction entière prenant des valeurs entières sur l'ensemble des entiers non négatifs. Si
une fonction entière prenant des valeurs entières sur l'ensemble des entiers non négatifs. Si
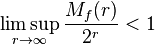 alors
alors 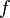 est un polynôme.
est un polynôme.
Autrement dit, la plus petite (au sens de la croissance) fonction entière non polynomiale qui prend des valeurs entières sur les entiers naturels est la fonction 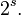
Ces résultats ont été généralisés aux fonctions entières prenant des valeurs entières sur une suite géométrique...
La théorie des fonctions entières d'ordre infini de Kraft-Blumenthal
Une fonction entière est d'ordre infini lorsqu'elle n'est pas d'ordre fini. Il avait été remarqué très tôt par Emile Borel que, dans le cas des fonctions entières d'ordre fini 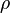 , s'il existait une infinité de cercles de rayon r sur lesquels la croissance était de l'ordre de
, s'il existait une infinité de cercles de rayon r sur lesquels la croissance était de l'ordre de 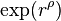 , il était possible que la croissance soit d'un ordre sensiblement inférieur sur une infinité d'autres cercles. Ces fonctions sont dites à croissance irrégulière. Le même phénomène existe pour les fonctions d'ordre infini.
, il était possible que la croissance soit d'un ordre sensiblement inférieur sur une infinité d'autres cercles. Ces fonctions sont dites à croissance irrégulière. Le même phénomène existe pour les fonctions d'ordre infini.
La théorie repose sur l'existence de fonctions types et sur la définition de l'ordre 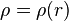 selon la formule
selon la formule
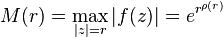
Applications de la théorie des fonctions entières
La théorie des fonctions entière permet, par le théorème de Liouville, de démontrer de manière simple et élégante le théorème fondamental de l'algèbre.
Cette théorie apparaît aussi dans la démonstration de l'existence d'une infinité de zéros de la fonction zêta de Riemann dans la bande par la propriété que les fonctions entières d'ordre non entier ont une infinité de zéros.
La théorie permet aussi l'étude des fonctions méromorphes comme quotients de deux fonctions entières. Les fonctions méromorphes apparaissant naturellement dans nombre de problèmes d'équations différentielles.
Ces méthodes restent aussi une source d'inspiration importante pour l'étude des fonctions analytiques plus compliquées, avec plusieurs variables...
Bibliographie
Barnes, A memoir on integral functions, philosophical transactions of the royal society of London, série A, Volume 199, 1902, p. 411-500
Boas, entire functions, Dover, 1954,
Borel, les fonctions entières, Gauthier-Villars, 1928 (deuxième édition)
Blumenthal, Les fonctions entières d'ordre infini, Cahiers scientifiques, 1914
Levin, Lectures on entire functions, AMS,1996
Nevanlinna, Le théorème de Picard-Borel et la théorie des fonctions méromorphes, Monographies sur la théorie des fonctions, Gauthier-Villars, 1929
Valiron, Fonctions convexes et fonctions entières, Bulletin de la SMF, T60, 1932
Valiron, Les fonctions entières d'ordre nul et d'ordre fini, thèse, 1914
Valiron, Fonctions entières d'ordre fini et fonctions méromorphes,
Valiron, Lectures on the general theory of integral functions, Chelsea Publishing, 1949
Valiron, Fonctions entières et fonctions méromorphes d'une variable, mémorial des sciences mathématiques, Gauthier-Villars, 1925.

 词典释义:
词典释义:
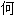 ,
,
 个;
个;
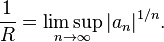
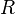 entre le point
entre le point 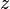 et la singularité la plus proche.
et la singularité la plus proche.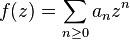
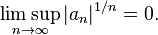
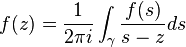
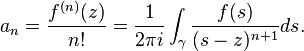
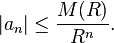
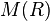 est alors borné quel que soit
est alors borné quel que soit 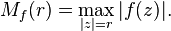
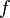 .
.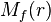 est une fonction convexe de ln r. (Hadamard)
est une fonction convexe de ln r. (Hadamard)
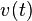 croissante (mais pas nécessairement continue) telle que
croissante (mais pas nécessairement continue) telle que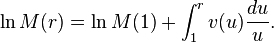
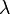 , on a
, on a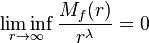
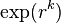 . Si l'on a, à partir d'une valeur
. Si l'on a, à partir d'une valeur 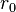 de
de  , l'inégalité
, l'inégalité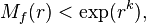
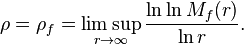
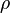 , les fonctions de type
, les fonctions de type 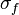 défini par la formule
défini par la formule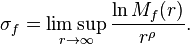
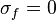 ), normal (
), normal (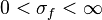 ) ou maximal (
) ou maximal ( ).
).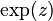 est d'ordre 1 ainsi que les fonctions
est d'ordre 1 ainsi que les fonctions 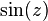 et
et 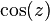 .
.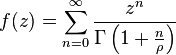
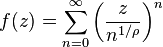
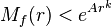
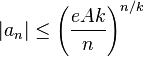
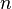 suffisamment grand.
suffisamment grand.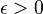 ,
,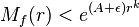
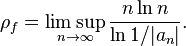
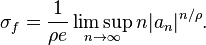
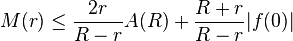
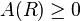
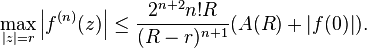
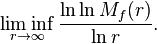
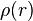 ayant les propriétés suivantes
ayant les propriétés suivantes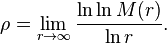
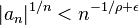
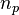 telle que
telle que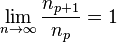
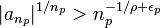
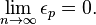
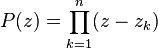 en dehors du voisinage des zéros. On suppose que l'on connaît
en dehors du voisinage des zéros. On suppose que l'on connaît 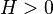 , on a
, on a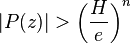
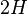 .
.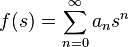 une fonction entière. La série
une fonction entière. La série 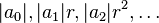 est une série décroissante à partir d'un certain rang et tendant vers 0, quel que soit
est une série décroissante à partir d'un certain rang et tendant vers 0, quel que soit 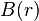 la valeur de ce terme et soit
la valeur de ce terme et soit 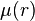 le rang (le plus grand, s'ils sont plusieurs) de ce terme.
le rang (le plus grand, s'ils sont plusieurs) de ce terme. 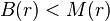 .
.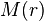 et
et ![B(r) < M(r) < B(r)\left[2\mu\left(r+ \frac{r}{\mu(r)}\right)+1\right]](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/2868115584202f7f78432a9791aa8064.png)
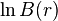 et
et 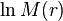 sont asymptotiquement égales.
sont asymptotiquement égales.
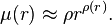
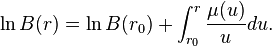
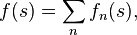
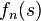 est inférieure à
est inférieure à 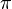 lorsque
lorsque 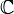 . Donc, plus un polynôme admet de zéros, plus il croît rapidement.
. Donc, plus un polynôme admet de zéros, plus il croît rapidement.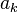 , ne présentant aucun pôle dans le disque
, ne présentant aucun pôle dans le disque 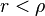 et en posant
et en posant 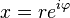
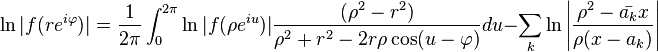
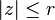 contenant les zéros
contenant les zéros 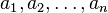 . Alors
. Alors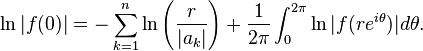
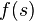 une fonction entière ayant tous ses zéros
une fonction entière ayant tous ses zéros 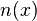 le nombre de zéros de modules inférieurs ou égaux à
le nombre de zéros de modules inférieurs ou égaux à 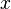 .
.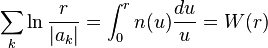
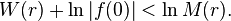
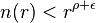 .
.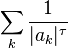
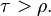
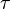 la plus petite pour laquelle la série converge. On en déduit donc ce théorème de Borel
la plus petite pour laquelle la série converge. On en déduit donc ce théorème de Borel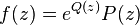 ou
ou 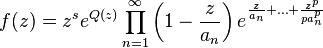 sans que cette décomposition puisse se faire pour p-1, où Q est un polynôme de degré p au plus, P, un polynôme quelconque et le produit infini le produit de Weierstrass.
sans que cette décomposition puisse se faire pour p-1, où Q est un polynôme de degré p au plus, P, un polynôme quelconque et le produit infini le produit de Weierstrass.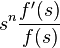 tend vers 0 uniformément quand
tend vers 0 uniformément quand 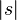 tend vers l'infini.
tend vers l'infini.
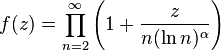
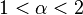 est d'ordre 1, et de genre 0 mais
est d'ordre 1, et de genre 0 mais 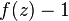 est de genre 1. De même
est de genre 1. De même 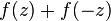 est de genre 1 mais
est de genre 1 mais 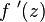 est de genre 0.
est de genre 0.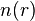 le nombre des zéros de module inférieur ou égal à
le nombre des zéros de module inférieur ou égal à 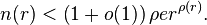
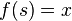 , quelle que soit la valeur de
, quelle que soit la valeur de 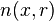 des racines de l'équation
des racines de l'équation 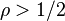 est d'ordre
est d'ordre 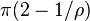 .
.
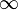 .
.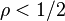 et d'ordre précisé L
et d'ordre précisé L 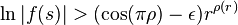
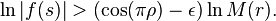
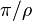 .
.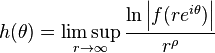
![\theta \in [-\pi,\pi]](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/87349317c914d3839f7ad62d8091edab.png) puisque la croissance sur une demi-ligne se répercute sur les lignes voisines.
puisque la croissance sur une demi-ligne se répercute sur les lignes voisines.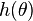 est l'indicatrice de de Phragmén-Lindelöf. C'est une fonction périodique de période
est l'indicatrice de de Phragmén-Lindelöf. C'est une fonction périodique de période 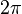 qui peut prendre des valeurs réelles, mais peut être
qui peut prendre des valeurs réelles, mais peut être 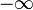 ou
ou 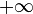 .
.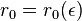 tel que pour tout
tel que pour tout 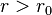 , on ait
, on ait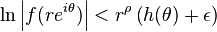
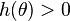 est de longueur supérieure à
est de longueur supérieure à 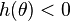 est de longueur inférieure ou égale à
est de longueur inférieure ou égale à 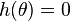 et d'un intervalle où
et d'un intervalle où 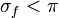 . La fonction f est entièrement déterminée par les valeurs f(n), pour n=1, 2, … De plus, si le type est strictement inférieur à ln 2, alors
. La fonction f est entièrement déterminée par les valeurs f(n), pour n=1, 2, … De plus, si le type est strictement inférieur à ln 2, alors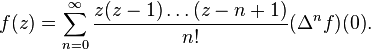
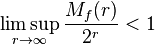
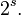
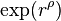 , il était possible que la croissance soit d'un ordre sensiblement inférieur sur une infinité d'autres cercles. Ces fonctions sont dites à croissance irrégulière. Le même phénomène existe pour les fonctions d'ordre infini.
, il était possible que la croissance soit d'un ordre sensiblement inférieur sur une infinité d'autres cercles. Ces fonctions sont dites à croissance irrégulière. Le même phénomène existe pour les fonctions d'ordre infini.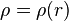 selon la formule
selon la formule