En analyse fonctionnelle et vectorielle, on appelle différentielle d'ordre 1 d'une fonction en un point a (ou dérivée de cette fonction au point a) la partie linéaire de l'accroissement de cette fonction entre a et a + h lorsque h tend vers 0. Elle généralise aux fonctions de plusieurs variables la notion de nombre dérivé d'une fonction d'une variable réelle, et permet ainsi d'étendre celle de développements limités. Cette différentielle n'existe pas toujours, et une fonction possédant une différentielle est appelée une fonction différentiable. On peut ensuite calculer des différentielles d'ordre supérieur à 1.
On utilise la notation différentielle avec beaucoup d'efficacité dans le cadre du calcul d'approximations et du calcul de dérivées. Elle facilite la formule de la dérivée de la composée. Elle se révèle très pratique dans le changement de variable en calcul intégral.
Dans l'approche de Leibniz, la différentielle d'une fonction est son « accroissement infinitésimal », qui s'écrit comme une combinaison des accroissements infinitésimaux des différentes variables. Ainsi pour une fonction f des variables x et y, son accroissement infinitésimal df s'exprime sous la forme :
-
où ∂ f ∂ x {\displaystyle {\frac {\partial f}{\partial x}}} et ∂ f ∂ y {\displaystyle {\frac {\partial f}{\partial y}}} sont les dérivées partielles de f.
Le calcul différentiel ainsi conçu, s'il était un outil de calcul efficace, manquait d'un fondement rigoureux, en particulier en ce qui concerne la notion de quantité infinitésimale. La notion moderne de différentielle est l'outil algébrique qui permet de passer des accroissements finis δx, δy des variables à l'accroissement δf de la fonction, en se limitant au premier ordre d'approximation. Mathématiquement, il n'est plus question de petite variation mais de calcul au premier ordre, dont la définition s'exprime sous forme d'une limite.
Il convient cependant de ne pas négliger la puissance d'évocation et l'efficacité dans les calculs du point de vue original de Leibniz. C'est ce qui explique qu'il reste massivement utilisé, notamment par les physiciens. En introduisant la notion avancée de calcul tensoriel sur les variétés, les mathématiciens ont pu assurer un statut précis aux notations différentielles de tous ordres.
Première approche
Fonction d'une seule variable
Le calcul différentiel, pour les fonctions d'une seule variable, se confond avec la dérivation. Soit f une fonction d'une variable réelle, à valeurs réelles ; on notera y = f(x) le résultat de l'application de f. Elle est dite dérivable en a lorsqu'il existe un réel, noté f'(a), tel que pour tout réel h on ait :
-
où ε est une fonction ayant une limite nulle en 0. f'(a) est alors appelé nombre dérivé de f en a. On résume souvent cela par la notation (dite notation de Landau)
-
Intuitivement ce calcul de limite, qui porte le nom de développement limité à l'ordre 1 pour la fonction f en a, signifie qu'en première approximation, pour h proche de 0, la valeur de f(a + h) est peu différente de celle de f ( a ) + f ′ ( a ) h {\displaystyle f(a)+f'(a)h} . Notamment parmi les expressions affines (i. e. de la forme α + βh), c'est celle-ci qui donne la meilleure approximation de f(a + h).
Introduction intuitive des notations du calcul infinitésimal
Dans de nombreuses applications, des notations parlantes sont employées pour décrire cette situation. On convient de noter le nombre h par dx pour indiquer qu'il représente une très petite variation de x par rapport à la valeur de référence a. On note dy la variation de l'image par rapport à la valeur de référence :
-
Le point de vue couramment adopté (surtout en physique), abusif en toute rigueur, est que pour des variations suffisamment petites, on peut écrire
. Cette présentation escamote en effet la nécessité d'utiliser un calcul de limite, car même pour des variations très petites, le terme d'erreur noté o(h) ci-dessus n'a pas de raison d'être nul. Mathématiquement parlant il serait plus juste de noter cela
-
car les mathématiciens prouvent la formule exacte
, en donnant aux notations dx et dy un sens précis qui n'est pas celui de petites variations et qui sera détaillé plus bas.
Fonction de deux variables
Soit f une fonction des deux variables x et y ; on notera z = f(x, y) le résultat de l'application de f.
Valeur attendue pour la différentielle
De nouveau, la question posée peut être formulée ainsi : lorsque, par rapport à des valeurs de référence a et b, on augmente les variables x et y des quantités dx et dy, quel est l'effet (au premier ordre) sur la variable z ?
Les dérivées partielles permettent de répondre à la question lorsqu'une des deux variations est nulle. Ainsi, parce que c'est un simple calcul de dérivée de fonction d'une variable, il est possible d'écrire
-
et de même en inversant les rôles : si dx est nul, dz se calcule à l'aide de la deuxième dérivée partielle.
Il semblerait naturel que lorsqu'on augmente x et y respectivement des quantités dx et dy, l'augmentation totale soit obtenue en superposant les deux cas précédents
-
ce qu'en physique on énonce en général sous la forme : la différentielle totale est la somme des différentielles partielles.
-
On écrira par exemple : si
alors
De fait, cette formule sera vérifiée dans de très nombreux calculs explicites ; mais elle n'est pas vraie en toute généralité.
Le problème de la différentiabilité
Il faut détailler le raisonnement pour voir où il pèche : on peut faire subir d'abord une augmentation de dx à la seule variable x, ce qui la fait passer de la valeur a à a + dx, tandis que y reste égal à b. Puis, en maintenant x = a + dx constant, on fait passer y de b à b + dy. Les accroissements de z résultants sont donc plus précisément
-
et encore si cette deuxième quantité existe effectivement.
L'existence de dérivées partielles au seul point (a, b) est a priori insuffisant pour écrire une formule générale de calcul de dz. En revanche, si l'on suppose que les dérivées partielles sont définies et continues sur un voisinage de (a, b), on pourra effectivement affirmer que dz a la valeur attendue.
Définition de la différentielle
En termes généraux, la différentiabilité est l'existence d'un développement limité à l'ordre 1 en un point, et la différentielle est la partie d'ordre 1 (donc linéaire) exactement.
Pour une fonction réelle à deux variables
Étudions en premier lieu une fonction de deux variables, à valeurs réelles : on notera z = f(x, y). Cette fonction sera dite différentiable au point a de coordonnées (x, y) s'il existe une formule de développement limité d'ordre 1 pour la fonction en ce point, c'est-à-dire
-
avec α et β des coefficients réels, ou encore
-
La limite est à prendre au sens des limites de fonctions de deux variables.
Si la fonction est différentiable, on montre que les coefficients α et β sont bien les dérivées partielles de f. On peut alors écrire
-
avec l'expression suivante qui est linéaire en
-
L'application linéaire L est appelée différentielle de f au point a et notée
.
On peut reprendre l'interprétation intuitive de L. Si les variables subissent une petite modification
, l'effet sur la fonction est une modification
, à condition de s'empresser d'ajouter : du moins au premier ordre.
Généralisations en dimension finie
Cette première notion se généralise aux fonctions de
dans
, en changeant simplement le nombre de variables, puis aux fonctions de
dans
en admettant des coefficients vectoriels pour le développement limité. Une fonction
de
dans
sera dite différentiable en a s'il existe un développement de la forme
-
avec ∥ h → ∥ {\displaystyle \|{\vec {h}}\|} qui désigne la norme du vecteur de composantes ( h 1 , . . . , h n ) {\displaystyle (h_{1},...,h_{n})} . Cette condition peut aussi s'écrire comme
-
La limite est à prendre au sens des limites de fonctions de n variables. De nouveau, si la fonction est différentiable, on montre que les coefficients
apparaissant dans ce développement sont les dérivées partielles de
. On notera donc
-
Pour effectuer ce calcul il est judicieux d'introduire des représentations matricielles pour le vecteur h → {\displaystyle {\vec {h}}} et l'application linéaire d f → ( a ) {\displaystyle \mathrm {d} {\vec {f}}(a)} : c'est ce que l'on appelle la matrice jacobienne de l'application. C'est une matrice de dimension (n, p). Le calcul de d f → ( a ) ( h → ) {\displaystyle \mathrm {d} {\vec {f}}(a)({\vec {h}})} peut aussi être présenté comme un calcul de produit scalaire du vecteur h → {\displaystyle {\vec {h}}} avec le vecteur gradient de f au point a.
La différentiabilité de la fonction assure l'existence de dérivées partielles ; la réciproque est fausse : l'existence de dérivées partielles n'assure pas la différentiabilité de la fonction, ni même sa continuité.
Il existe cependant un résultat positif : si les dérivées partielles de f existent et sont continues, alors f est différentiable.
Si l'application f est linéaire, alors elle est différentiable en tout point a et df(a) = f. Ceci s'applique en particulier à chaque fonction coordonnée ℝ → ℝ, x ↦ xk — dont la dérivée en tout point a, dxk(a) : h ↦ hk, est simplement notée dxk — et justifie la réécriture suivante de la différentielle de
en a :
-
Différentiabilité au sens de Fréchet
Plus généralement, il est possible de définir la notion de différentiabilité et de différentielle sans avoir recours à des bases.
Soient E un espace vectoriel normé, F un espace vectoriel topologique séparé, f une application de E dans F et a un point de E. On abandonne la notation des vecteurs par des flèches dans ce paragraphe.
On dit que f est différentiable en a (au sens de Fréchet) s'il existe une application linéaire continue L : E → F telle que :
-
ou, de manière équivalente :
-
Une telle application linéaire L est alors unique. Elle est appelée différentielle de f en a et se note
. De plus, sa continuité assure la continuité en a de f.
Démonstration de l'unicité
Soit L' une application linéaire vérifiant également la définition de la différentielle de f en a. Posons u = L – L' et montrons que u = 0 (sans même utiliser l'hypothèse que L et L' sont continues). Soient s un vecteur de norme 1 dans E et V un voisinage de 0F. Puisque
, il existe un rayon α > 0 tel que
. Or par linéarité de u,
. Ainsi u(s) est dans tous les voisinages de 0F et donc u(s) = 0F par séparation de F. Par suite, u = 0 et L = L'.
La différentiabilité dépend de la norme choisie sur E ; on retrouve, ceci dit, la définition usuelle en dimension finie puisque toutes les normes y sont équivalentes.
On peut remarquer le changement sémantique entre la première définition, celle de Leibniz – un accroissement très petit –, et celle formalisée de nos jours – une application linéaire. Ce changement est l'aboutissement d'une évolution de plus de trois siècles entre une idée intuitive du calcul infinitésimal et sa formalisation.
Différentielle d'ordre supérieur
Cas de la fonction réelle
Si y = f(x), si f est dérivable sur I, alors d f = f ′ ( x ) d x {\displaystyle \mathrm {d} f=f'(x)\mathrm {d} x} . Si de plus, f' est dérivable, df est différentiable et
-
. Cette quantité s'appelle la différentielle d'ordre 2 de f.
Plus généralement, si f est n fois dérivable sur I, on appelle différentielle d'ordre n sur I, l'expression
-
Cas de la fonction réelle à deux variables
Si f est une fonction différentiable sur I (ouvert de R 2 {\displaystyle \mathbb {R} ^{2}} ), alors d f = ∂ f ∂ x d x + ∂ f ∂ y d y {\displaystyle \mathrm {d} f={\tfrac {\partial f}{\partial x}}\mathrm {d} x+{\tfrac {\partial f}{\partial y}}\mathrm {d} y} , chacune des fonctions ∂ f ∂ x {\displaystyle {\tfrac {\partial f}{\partial x}}} et ∂ f ∂ y {\displaystyle {\tfrac {\partial f}{\partial y}}} est elle-même une fonction de R 2 {\displaystyle \mathbb {R} ^{2}} dans R {\displaystyle \mathbb {R} } . Si elles sont de classe C (c'est-à-dire différentiables de différentielle continue) alors df est aussi différentiable et
-
Comme les différentielles sont continues, le théorème de Schwarz permet de dire que :
-
ce qui permet d'écrire la différentielle d'ordre 2 de f sous la forme suivante :
-
où
devient un opérateur agissant sur f.
Plus généralement, si f est de classe C alors (formellement, dans l'algèbre des opérateurs)
-
Cas général
On considère deux espaces vectoriels normés E et F, U un ouvert de E et f : U → F.
On dit que f est deux fois différentiable en
si :
f est différentiable en a (de différentielle f ′ ( a ) ∈ L ( E , F ) {\displaystyle f'(a)\in {\mathcal {L}}(E,F)} )
l'application f ′ : U → L ( E , F ) {\displaystyle f':U\to {\mathcal {L}}(E,F)} est différentiable en a (au sens de la métrique induite sur L ( E , F ) {\displaystyle {\mathcal {L}}(E,F)} ).
L'application dérivée seconde est donc une fonction
et la différentielle seconde en a est l'application
. Mais intéressons-nous de plus près à
. Il s'agit d'une fonction
linéaire. De même, une fois choisi
l'application
est linéaire
L'application f ″ ( a ) {\displaystyle f''(a)} peut donc être interprétée comme une application bilinéaire f ″ ( a ) : E × E → F {\displaystyle f''(a):E\times E\to F} associant ∀ ( x , y ) ∈ E × E , f ″ ( a ) ( x , y ) := ( ( f ′ ) ′ ( a ) x ) y . {\displaystyle \forall (x,y)\in E\times E,f''(a)(x,y):=((f')'(a)x)y.}
De manière générale, on définit la différentielle d'ordre n de f en a comme l'application n-linéaire f ( n ) ( a ) : E n → F , ( x 1 , . . . , x n ) ↦ ( . . . ( ( f ( n ) ( a ) x 1 ) x 2 ) . . . ) x n . {\displaystyle f^{(n)}(a):E^{n}\to F,(x_{1},...,x_{n})\mapsto (...((f^{(n)}(a)x_{1})x_{2})...)x_{n}.}
Note
1 2 Il est cependant possible de réintroduire de manière rigoureuse la notion d’infiniment petit ; voir l'article Analyse non standard

 词典释义:
词典释义:
 择吸附
择吸附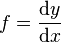 。
。