Une planche de l'Encyclopédie de Diderot et d'Alembert illustrant l'article « Carreleur ».
En mathématiques, la combinatoire, appelée aussi analyse combinatoire, étudie les configurations de collections finies d'objets ou les combinaisons d'ensembles finis, et les dénombrements.
Généralités et historique
La combinatoire remonte à l'Antiquité : Plutarque rapporte ainsi une assertion de Chrysippe « contredite par tous les mathématiciens, et entre autres par Hipparque », sur le nombre de façons de combiner dix propositions. Hipparque savait que le nombre de « propositions composées positives » que l'on peut former à partir de dix propositions simples est 103 049, et que le nombre de propositions négatives est 310 952. Cet affirmation est restée inexpliquée jusqu'en 1994, quand David Hough, un étudiant de l'université George Washington, observe qu'il y a 103 049 façons de parenthéser une suite de dix éléments. Une explication semblable peut être donnée pour le deu**ème nombre : il est très proche de (103 049 + 518 859)/2 = 310 954, qui est la moyenne des di**ème et onzième nombres de Schröder-Hipparque, et qui compte le nombre de parenthésages de dix termes avec un signe.
Parmi les autres précurseurs, on peut citer Bhāskara II au **I siècle (nombre de choix de p éléments parmi n), Raymond Lulle au **II siècle, Gersonide au début du **V siècle (rapport entre le nombre d'arrangements et le nombre de combinaisons), Michael Stifel au XVI siècle (première approche du triangle de Pascal). Elle se développe de façon significative à partir du XVII siècle, en même temps que le calcul des probabilités, avec Blaise Pascal et Pierre de Fermat. Initialement, elle avait pour objet la résolution des problèmes de dénombrement, provenant de l'étude des jeux de hasard. Plus tard, elle se lia à la théorie des nombres et à la théorie des graphes.
En particulier, la combinatoire s'intéresse aux méthodes permettant de compter les éléments dans des ensembles finis (combinatoire énumérative) et à la recherche des optima dans les configurations ainsi qu'à leur e**stence (combinatoire extrémale).
Voici quelques exemples de situations donnant lieu à des questions d'analyse combinatoire :
les rangements de livres sur une étagère ;
les dispositions de personnes autour d'une table ronde ;
les tirages avec remise d'un certain nombre de boules numérotées dans une urne ;
les placements de jetons sur un damier ;
le nombre d'ordonnancements possibles des cartes d'un jeu de 52 cartes. Dans ce dernier exemple, le nombre est égal à 52! (le « ! » dénotant la factorielle). Il peut sembler étonnant que ce nombre, environ 8,065 817 517 094 ×10, soit si grand. C'est environ 8 suivi de 67 zéros. Il est, par exemple, beaucoup plus grand que le nombre d'Avogadro, égal à 6,022 ×10.
Domaines de la combinatoire
Combinatoire énumérative
Cinq arbres binaires à trois sommets, un exemple de nombre de Catalan.
La combinatoire énumérative est le domaine le plus classique de la combinatoire, et s'intéresse au dénombrement de certains objets combinatoires. Même si le dénombrement des éléments d'un ensemble est un problème mathématique plutôt vaste, de nombreux problèmes qui se présentent dans diverses applications ont des descriptions combinatoires plutôt simples. La suite des nombres de Fibonacci est un exemple de base d'un problème de combinatoire énumérative. Il e**ste un modèle appelé en anglais Twelvefold way (en) qui constitue un cadre unifié pour les problèmes de dénombrement des permutations, combinaisons et partitions.
La combinatoire moderne comporte de nombreux champs très développés, et utilise des outils puissants empruntés à des branches mathématiques parfois inattendues ; on distingue ainsi :
Théorie combinatoire des nombres
La combinatoire arithmétique (en) s'occupe des problèmes de théorie des nombres qui impliquent les idées combinatoires dans leurs formulations ou leurs solutions. Paul Erdős est le principal fondateur de cette branche de la théorie des nombres. Les sujets caractéristiques incluent les systèmes couvrants, les problèmes à somme zéro, diverses sommes d'ensembles restreintes et des progressions arithmétiques dans l'ensemble des entiers. Les méthodes algébriques ou analytiques sont puissantes dans ce champ d'étude.
Combinatoire des mots
Construction de la suite de Prouhet-Thue-Morse.
La combinatoire des mots applique l'analyse combinatoire aux mots finis ou infinis. Cette branche s'est développée à partir de plusieurs branches des mathématiques : la théorie des nombres, la théorie des groupes, les probabilités et bien sûr la combinatoire. Elle a des liens avec divers thèmes informatiques, comme la recherche de motifs dans un texte ou la compression de textes.
Combinatoire algébrique
La combinatoire algébrique est une discipline qui traite de l'étude des structures algébriques par des techniques algorithmiques et combinatoires, comme notamment illustré par les travaux de Marcel-Paul Schützenberger, Alain Lascoux, Dominique Foata et Richard Stanley. L'intérêt de la combinatoire algébrique vient du fait que la plupart des structures en algèbre abstraite sont soit finies, soit engendrées par un ensemble fini d'éléments, ce qui rend possible leur manipulation de manière algorithmique.
Combinatoire analytique
La combinatoire analytique (en anglais : analytic combinatorics) est un ensemble de techniques décrivant des problèmes combinatoires dans le langage des séries génératrices, et s'appuyant en particulier sur l'analyse complexe pour obtenir des résultats asymptotiques sur les objets combinatoires initiaux. Les résultats de combinatoire analytique permettent notamment une analyse fine de la ** de certains algorithmes.
Combinatoire probabiliste

Chemin sans contact dans une grille.
La combinatoire probabiliste ou méthode probabiliste est une méthode non constructive, initialement utilisée en combinatoire et lancée par Paul Erdős, pour démontrer l'e**stence d'un type donné d'objet mathématique. Cette méthode a été appliquée à d'autres domaines des mathématiques tels que la théorie des nombres, l'algèbre linéaire et l'analyse réelle. Son principe est de montrer que si l'on choisit au hasard des objets d'une catégorie, la probabilité que le résultat soit d'un certain type est plus que zéro. Bien que la démonstration utilise la théorie des probabilités, la conclusion finale est déterminée de façon certaine.
Combinatoire topologique
Partage de collier (en) avec deux coupes.
En combinatoire topologique, on utilise des concepts et méthodes de la topologie dans l'étude de problèmes comme la coloration de graphe, le partage équitable, la partition d'un ensemble, les posets (ensembles partiellement ordonnés), les arbres de décision, le problème du partage de collier (en) ou la théorie de Morse discrète (en). Ne pas confondre avec la topologie combinatoire qui est une ancienne dénomination pour topologie algébrique.
Combinatoire géométrique
Icosaèdre.
La combinatoire géométrique inclut un certain nombre de thèmes comme la combinatoire des polyèdres (étude des faces de polyèdres convexes), la géométrie convexe (étude des ensembles convexes, en particulier la combinatoire de leurs intersections), et la géométrie discrète, qui à son tour a de nombreuses applications en géométrie algorithmique. D'autres domaines important sont la géométrie métrique des polyèdres, tels que le théorème de Cauchy sur la rigidité des polytopes convexes. L'étude des polytopes réguliers, des solides d'Archimède, ou des Kissing number (en)s font également partie de la combinatoire géométrique. Des polytopes particulier sont aussi considérés, comme le permutoèdre, l'associaèdre et le polytope de Birkhoff (en) (sur les matrices bistochastiques).
Combinatoire extrémale et Théorie de Ramsey
La théorie de Ramsey, nommée d'après Frank Ramsey, tente typiquement de répondre à des questions de la forme : « combien d'éléments d'une certaine structure doivent être considérés pour qu'une propriété particulière se vérifie ? » Un exemple type est le théorème de Ramsey qui affirme que, pour tout entier n, tout graphe complet suffisamment grand dont les arêtes sont colorées contient des sous-graphes complets de taille n d'une seule couleur.
Domaines connexes
De plus, on rencontre des outils combinatoires dans les domaines suivants :
Théorie des graphes
Graphe de Petersen.
La théorie des graphes est une théorie informatique et mathématique. Les algorithmes élaborés pour résoudre des problèmes concernant les objets de cette théorie ont de nombreuses applications dans tous les domaines liés à la notion de réseau et dans bien d'autres domaines, tant le concept de graphe est général. De grands théorèmes difficiles, comme le théorème des quatre couleurs, le théorème des graphes parfaits, ou encore le théorème de Robertson-Seymour, ont contribué à asseoir cette matière auprès des mathématiciens, et les questions qu'elle laisse ouvertes, comme la conjecture d'Hadwiger, en font une branche vivace des mathématiques discrètes.
Théorie des partitions
Diagrammes de Ferrers des partitions des entiers jusqu'à 8.
La théorie des partitions étudie divers problèmes d'énumération et de comportement asymptotique liés aux partitions d'un entier, et a des relations étroites avec les q-analogues, les fonctions spéciales et les polynômes orthogonaux. Au départ, elle fait partie de la théorie des nombres et de l'analyse. Elle est considérée maintenant comme une partie de la combinatoire, ou comme un domaine indépendant. Elle utilise l'approche par preuve bijective et employe divers outils d'analyse, de théorie analytique des nombres, et a des conne**ons avec la physique statistique.
Théorie des matroïdes
Un matroïde est un objet mathématiques introduit en 1935 par Whitney, qui a pour vocation initiale de saisir l'essence du concept d'indépendance linéaire. Elle est donc naturellement liée à l'algèbre linéaire et aussi à la théorie des graphes et à la géométrie.
Théorie des ordres
Hypercube.
Un poset (de l'anglais partially ordered set, en français "ensemble partiellement ordonné") formalise et généralise la notion intuitive d'ordre ou d'arrangement entre les éléments d'un ensemble. Un poset est un ensemble muni d'une relation d'ordre qui indique que pour certains couples d'éléments, l'un est plus petit que l'autre. Tous les éléments ne sont pas forcément comparables, contrairement au cas d'un ensemble muni d'un ordre total. Si l'ensemble est fini, on dispose d'une représentation graphique du poset, qui est diagramme de Hasse.
Block design
Un 'block design est formé d'un ensemble muni et d'une famille de sous-ensembles (distincts ou non selon les cas). Ces sous-ensembles sont choisis de manière à satisfaire certaines propriétés correspondant à une application particulière. Les applications viennent de domaines varies, y compris plan d'expérience, géométrie finie, test de logiciel, cryptographie, et géométrie algébrique. De nombreuses variantes ont été étudiées, les plus considérés sont les block designs équilibrés incomplets.
Séries génératrices
Une série génératrice est une série formelle dont les coefficients codent une suite de nombres (ou plus généralement de polynômes, etc.). Il e**ste plusieurs sortes de séries génératrices, comme les séries génératrices exponentielles, les séries de Lambert, les séries de Dirichlet, etc. On peut associer à toute suite une série génératrice de chaque type, mais la facilité de manipulation de la série dépend considérablement de la nature de la suite associée, et du problème qu'on cherche à étudier. L'intérêt des séries est qu'il est souvent possible d'étudier une suite donnée à l'aide de manipulations formelles de la série génératrice associée, ainsi qu'en utilisant les propriétés analytiques de la fonction somme de la série.
Permutations (dispositions, ordonnancements)
Permutations sans répétition d'objets discernables
Les permutations sans répétition d'un ensemble fini E sont les bijections de E sur lui-même.
Comme exemple d'introduction, considérons le nombre de dispositions de six objets discernables dans six cases consécutives numérotées avec un et un seul objet par case. Chacun des objets peut être placé dans la première case, ce qui donne six possibilités d'occuper la première place. Une fois la première place occupée par l'un des objets, il reste encore cinq candidats pour la deu**ème place, la deu**ème place étant attribuée, il reste seulement quatre candidats pour la troisième place, et ainsi de suite. Pour l'avant-dernière place, il ne reste plus que deux objets, et une fois l'un des deux placé, la dernière place doit être occupée par le dernier objet.
Il y a ainsi 6 × 5 × 4 × 3 × 2 × 1 ou 6! = 720 possibilités de disposer six objets discernables.
-
Généralisation
Nous allons voir que le nombre de dispositions de n éléments discernables est égal à n!
Une disposition des objets d'un ensemble E de cardinal n, dans n cases avec un et un seul objet par case, ou un ordonnancement des éléments de E se représente par une bijection de {1, 2, …, n} dans E ou une permutation de E. Il est commode de représenter une telle bijection par un n-uplet (ou n-liste) d'éléments de E, (x1, x2, …, xn).
Théorème — Il y a n! permutations (sans répétition) de n éléments.
En effet, pour former un n-uplet d'éléments de E, nous devons choisir un élément de E pour la première place du n-uplet et il y a n possibilités, il y a n - 1 choix possibles d'un élément de E pour la deu**ème place, n - 2 pour la troisième etc. Il n'y a plus qu'un seul choix d'élément pour la dernière place. Donc au total n × (n-1) × (n-2) × … × 2 × 1 permutations.
Cette propriété se démontre par récurrence sur n.
Permutations avec répétition d'objets discernables
Pour déterminer le nombre des dispositions possibles d'objets de plusieurs classes et mutuellement indiscernables dans chaque classe, il est utile de considérer le nombre de dispositions possibles de ces objets en les supposant tous discernables, et ensuite de trouver combien de ces dispositions sont indiscernables. Le nombre des dispositions possibles de ces objets est égal au nombre de dispositions possibles des objets considérés comme discernables divisé par le nombre des dispositions indiscernables.
Par exemple, si nous devons déterminer le nombre total de dispositions d'objets dont deux sont d'une première classe, trois d'une deu**ème classe et cinq d'une troisième classe, alors nous calculons le nombre total de dispositions de ces objets considérés comme discernables, ce qui donne (2 + 3 + 5)!, soit 3 628 800 dispositions possibles. Mais certaines dispositions restent inchangées lorsque les objets indiscernables d'une même classe sont échangés mutuellement, et il y a 2! × 3! × 5! soit 1 440 façons de permuter les objets de chacune de ces classes.
Nous obtenons au total 3 628 800 ÷ 1 440 = 2 520 dispositions différentes. Il s'agit aussi du nombre de permutations avec répétition de 10 éléments avec 2, 3 et 5 répétitions.
-
Généralisation
Théorème — Le nombre de permutations de n éléments, répartis dans k classes dont n1 sont de classe 1, n2 sont de classe 2, …, nk sont de classe k, indiscernables dans chaque classe, ou le nombre de permutations de n éléments avec n1, n2, …, nk répétitions, avec 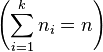 , est égal à :
, est égal à : 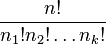 .
.
Arrangements (choix en tenant compte de l'ordre)
Arrangements sans répétition
Nous disposons de n objets discernables et nous voulons en placer k, en tenant compte de l'ordre, dans k cases numérotées de 1 à k avec un et un seul objet par case. Le nombre de dispositions est alors égal au nombre de k-listes distinctes formées à partir de ces objets. Au lieu de constituer un n-uplet, à partir de n objets discernables, nous formons ici des k-uplets avec à partir de ces n objets tels que pour , on ait . Un tel k-uplet s'appelle un arrangement sans répétition de n éléments pris k à k.
Théorème — Le nombre d'arrangements sans répétition de n éléments pris k à k est égal à  (égal à
(égal à 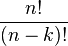 si k≤n et à 0 sinon).
si k≤n et à 0 sinon).
En effet, Il y a n choix possibles de l'objet qui occupe la première place du k-uplet, n-1 choix pour l'objet de la 2 place ; pour la k, il ne reste plus que n-(k-1) objets et donc n-k+1 choix possibles. Le produit s'écrit bien sous la forme : . C'est juste le nombre des injections de l'ensemble {1,2, ..., k} dans l'ensemble {1,2, ..., n}.
Le cas n = k nous oblige alors à diviser par (0)! (rappelons que (0)! vaut 1).
Arrangements avec répétition
Lorsque nous voulons placer des objets pris parmi n objets discernables dans k emplacements en tenant compte de l'ordre, ces objets pouvant apparaître plusieurs fois, le nombre de dispositions est alors égal au nombre de k-uplets formés à partir de ces n objets. Un tel k-uplet, avec k≤n, (x1, x2, …, xk) formé à partir de ces n objets s'appelle un arrangement avec répétition de n éléments pris k à k.
Comme chaque emplacement peut être occupé indifféremment par l'un quelconque de ces n objets, il y en a au total n.
Quand nous tirons 11 fois l'un de 3 numéros en tenant compte de l'ordre d'apparition nous obtenons au total 3 = 177 147 tirages différents. Comme exemple tiré de la génétique, nous pouvons donner le nombre total de codons de base (triplets formés de quatre codes) : 4= **.
Combinaisons (choix sans tenir compte de l'ordre)
Contrairement aux arrangements, les combinaisons sont des dispositions d'objets qui ne tiennent pas compte de l'ordre de placement de ces objets. Par exemple, si a, b et c sont des boules tirées d'une urne, abc et acb correspondent au même tirage. Il y a donc moins de combinaisons que d'arrangements.
Combinaisons sans répétition
Si nous tirons sans remise k objets parmi n objets discernables, et nous les disposons sans tenir compte de l'ordre d'apparition, nous pouvons représenter ces k objets par une partie à k éléments d'un ensemble à n éléments. Ce sont des combinaisons sans répétition de n éléments pris k à k.
Pour déterminer le nombre de ces dispositions, nous pouvons déterminer le nombre d'arrangements de k objets et diviser par le nombre de dispositions obtenues les unes à partir des autres par une permutation. Il y en a (pour la notation, voir aussi l'article sur le coefficient binomial).
Par exemple le jeu Euromillions demande de choisir 5 nombres différents entre 1 et 50 et 2 nombres entre 1 et 11, soit possibilités.
Combinaisons avec répétition
Si nous tirons avec remise k objets parmi n objets discernables, et nous les disposons sans tenir compte de l'ordre d'apparition, ces objets peuvent apparaître plusieurs fois et nous ne pouvons les représenter ni avec une partie à k éléments, ni avec un k-uplet puisque leur ordre de placement n'intervient pas. Il est cependant possible de représenter de telles dispositions avec des applications appelées combinaisons avec répétition.
Théorème — Le nombre de combinaisons avec répétition de n éléments pris k à k est égal à : 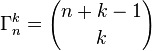 .
.
Donnons l'exemple du jeu de domino. Les pièces sont fabriquées en disposant côte à côte deux éléments de l'ensemble {blanc, 1, 2, 3, 4, 5, 6}. Si nous retournons un domino, nous changeons l'ordre des deux éléments, mais le domino reste identique. Nous avons une combinaison avec répétition de 7 éléments pris 2 à 2, et au total il y a : 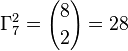 dominos dans un jeu.
dominos dans un jeu.
Fonction de comptage
Soit Sn l'ensemble des permutations de {1, 2, …, n}. Nous pouvons considérer la fonction qui à n associe le nombre de permutations. Cette fonction est la fonction factorielle et sert à compter les permutations.
Étant donnée une collection infinie d'ensembles finis 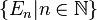 indexée par l'ensemble des entiers naturels, une fonction de comptage est une fonction qui à un entier n associe le nombre d'éléments de En. Une fonction de comptage f permet donc de compter les objets de En pour n'importe quel n. Les éléments de En ont habituellement une description combinatoire relativement simple et une structure additionnelle, permettant souvent de déterminer f.
indexée par l'ensemble des entiers naturels, une fonction de comptage est une fonction qui à un entier n associe le nombre d'éléments de En. Une fonction de comptage f permet donc de compter les objets de En pour n'importe quel n. Les éléments de En ont habituellement une description combinatoire relativement simple et une structure additionnelle, permettant souvent de déterminer f.
Certaines fonctions de comptage, sont données par des formules « fermées », et peuvent être exprimées comme composées de fonctions élémentaires telles que des factorielles, des puissances, et ainsi de suite.
Cette approche peut ne pas être entièrement satisfaisante (ou pratique) pour certains problèmes combinatoires. Par exemple, soit f(n) le nombre de sous-ensembles distincts de nombres entiers dans l'intervalle [1, n] qui ne contiennent pas deux nombres entiers consécutifs. Par exemple, avec n = 4, nous obtenons ∅, { 1 }, { 2 }, { 3 }, { 4 }, { 1, 3 }, { 1, 4 }, { 2, 4 }, et donc f(4) = 8. Il s'avère que f(n) est le nème nombre de Fibonacci, qui peut être exprimé sous la forme « fermée » suivante :
-
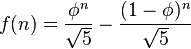
où Φ = (1 + √5)/2, est le nombre d'or. Cependant, étant donné que nous considérons des ensembles de nombres entiers, la présence du √5 dans le résultat peut être considérée comme inesthétique d'un point de vue combinatoire. Aussi f(n) peut-il être exprimé par une relation de récurrence :
-
f(n) = f(n - 1) + f (n - 2)
ce qui peut être plus satisfaisant (d'un point de vue purement combinatoire), puisque la relation montre plus clairement comment le résultat a été trouvé.
Dans certains cas, un équivalent asymptotique g de f,
-
f(n)~g(n) quand n tend vers l'infini
où g est une fonction « familière », permet d'obtenir une bonne appro**mation de f. Une fonction asymptotique simple peut être préférable à une formule « fermée » extrêmement compliquée et qui informe peu sur le comportement du nombre d'objets. Dans l'exemple ci-dessus, un équivalent asymptotique serait :
-

quand n devient grand.
Une autre approche est celle des séries entières. f(n) peut être exprimé par une série entière formelle, appelée fonction génératrice de f, qui peut être le plus couramment :
la fonction génératrice ordinaire
-
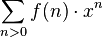
ou la fonction génératrice exponentielle
-
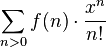
Une fois déterminée, la fonction génératrice peut permettre d'obtenir toutes les informations fournies par les approches précédentes. En outre, les diverses opérations usuelles comme l'addition, la multiplication, la dérivation, etc., ont une signification combinatoire ; et ceci permet de prolonger des résultats d'un problème combinatoire afin de résoudre d'autres problèmes.
Quelques résultats
Un théorème, dû à Franck P. Ramsey, donne un résultat surprenant. À une soirée à laquelle se rendent au moins six personnes, il y a au moins trois personnes qui se connaissent mutuellement ou au moins trois qui sont étrangères les unes aux autres.
-
Démonstration
soit 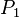 une personne quelconque présente à la soirée. Sur les n-1 autres, soit elle en connaît au plus deux, soit elle en connaît au moins trois. Supposons que l’on est dans le second cas, et soient
une personne quelconque présente à la soirée. Sur les n-1 autres, soit elle en connaît au plus deux, soit elle en connaît au moins trois. Supposons que l’on est dans le second cas, et soient 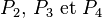 trois personnes connues de
trois personnes connues de 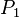 . Si deux d’entre elles se connaissent, mettons
. Si deux d’entre elles se connaissent, mettons 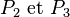 , alors
, alors 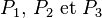 se connaissent toutes trois. Sinon,
se connaissent toutes trois. Sinon, 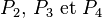 ne se connaissent pas du tout, et le résultat annoncé est encore juste. Dans l’autre cas de figure (
ne se connaissent pas du tout, et le résultat annoncé est encore juste. Dans l’autre cas de figure (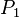 connaît au plus deux personnes du groupe), le même raisonnement, inversé, fonctionne avec les trois personnes que
connaît au plus deux personnes du groupe), le même raisonnement, inversé, fonctionne avec les trois personnes que 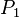 ne connaît pas.
ne connaît pas.
(C'est un cas particulier du théorème de Ramsey.)
L'idée de trouver un ordre dans des configurations aléatoires mène à la théorie de Ramsey. Essentiellement, cette théorie indique que n'importe quelle configuration suffisamment grande contiendra au moins un autre type de configuration.

 词典释义:
词典释义:
 词:
词:
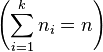 , est égal à
, est égal à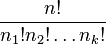 .
. (égal à
(égal à 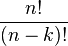 si k≤n et à 0 sinon).
si k≤n et à 0 sinon).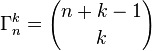 .
.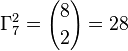 dominos dans un jeu.
dominos dans un jeu.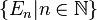 indexée par l'ensemble des entiers naturels, une fonction de comptage est une fonction qui à un entier n associe le nombre d'éléments de En. Une fonction de comptage f permet donc de compter les objets de En pour n'importe quel n. Les éléments de En ont habituellement une description combinatoire relativement simple et une structure additionnelle, permettant souvent de déterminer f.
indexée par l'ensemble des entiers naturels, une fonction de comptage est une fonction qui à un entier n associe le nombre d'éléments de En. Une fonction de comptage f permet donc de compter les objets de En pour n'importe quel n. Les éléments de En ont habituellement une description combinatoire relativement simple et une structure additionnelle, permettant souvent de déterminer f.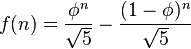

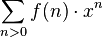
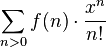
 une personne quelconque présente à la soirée. Sur les n-1 autres, soit elle en connaît au plus deux, soit elle en connaît au moins trois. Supposons que l’on est dans le second cas, et soient
une personne quelconque présente à la soirée. Sur les n-1 autres, soit elle en connaît au plus deux, soit elle en connaît au moins trois. Supposons que l’on est dans le second cas, et soient 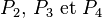 trois personnes connues de
trois personnes connues de 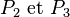 , alors
, alors 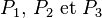 se connaissent toutes trois. Sinon,
se connaissent toutes trois. Sinon,