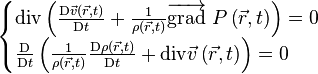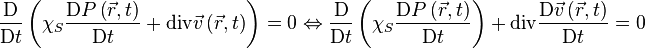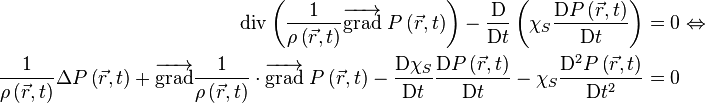Source sonore omni-directionnelle dans une chambre anéchoïque (Czech Technical Univerzity, Prague).
L’acoustique est la science du son, ce qui inclut sa production, son contrôle, sa transmission, sa réception et ses effets. Elle fait notamment appel à des notions de mécanique des fluides, de mécanique vibratoire, de mécanique du solide déformable et de thermodynamique.
Le terme acoustique fut introduit par Joseph Sauveur (1653-1716) : il est construit à partir du terme ἀκουστικός [akoustikos] provenant du grec ancien signifiant « de l'ouïe », lui-même provenant de ἀκούειν [akouein], signifiant « entendre ». Depuis, le mot acoustique englobe en physique toutes les ondes mécaniques au sein des gaz, des liquides, mais également au sein des solides, et ce quelle que soit la plage de fréquences considérée (les infrasons, les sons et les ultrasons).
L'acoustique comprend de nombreuses ramifications parmi lesquelles on rencontre l'électroacoustique (microphones, haut-parleurs), l'audition, l’acoustique musicale, etc.
L'acoustique a des applications dans les domaines des sciences de la terre et de l'atmosphère, des sciences de l'ingénieur, des sciences de la vie et de la santé, ainsi que dans les sciences humaines et sociales.
Histoire
Les principes de l'acoustique sont appliqués dès l'antiquité : Théâtre romain de Bosra, Syrie.
Science dont les bases remontent à l'Antiquité, Pythagore étudie au VI siècle av. J.-C. l'acoustique musicale, notamment les intervalles. Le théâtre d'Épidaure témoigne que dès le IV siècle av. J.-C. les grecs maîtrisaient les propriétés sonores des matériaux pour construire des amphithéâtres : l'agencement périodique des rangées de sièges du théâtre d'Épidaure permet de filtrer les basses fréquences (inférieures à 500 Hz) du bruit de fond (bruissement des arbres, auditoire).
Acoustique empirique
L'origine de l'acoustique est attribuée à Pythagore (VI siècle av. J.-C.), qui étudia le fonctionnement des cordes vibrantes produisant des intervalles musicaux plaisants à l'oreille. Ces intervalles sont à l'origine de l'accord pythagoricien portant aujourd'hui son nom. Aristote (IV siècle av. J.-C.) anticipa correctement que le son se générait de la mise en mouvement de l'air par une source « poussant vers l'avant l'air contigu de telle manière que le son voyage ». Son hypothèse était basée sur la philosophie plus que sur la physique expérimentale. D'ailleurs, il suggéra de manière erronée que les hautes fréquences se propageaient plus rapidement que les basses fréquences, erreur qui perdura plusieurs siècles.
La spéculation que le son est un phénomène ondulatoire doit son origine à l'observation des ondes à la surface de l'eau. En effet, la notion d'onde peut être considérée, de manière rudimentaire, comme une perturbation oscillatoire qui se propage à partir d'une source et ne transporte pas de matière sur des grandes distances de propagation. La possibilité que le son présente un comportement analogue fut notamment soulignée par le philosophe grec Chrysippe (III siècle av. J.-C.) et l'architecte et ingénieur romain Vitruve (environ 25 av. J.-C.), qui contribua par ailleurs à la conception de l'acoustique de théâtres antiques. Le philosophe romain Boèce (470-525 ap. J.-C.) formula aussi l'hypothèse d'un comportement similaire, de même qu'il suggéra que la pe****tion humaine de la hauteur était liée à la propriété physique de la fréquence.
Acoustique expérimentale, mesures et instrumentation acoustiques
Un premier résultat expérimental important fut obtenu au début du XVII siècle, dont la découverte est due principalement à Marin Mersenne et Galileo Galilei : le mouvement de l'air généré par un corps vibrant à une certaine fréquence est aussi un mouvement vibratoire de fréquence identique à la fréquence de vibration du corps vibrant. Dans l'Harmonie Universelle (1637), Mersenne décrivit la première détermination absolue de la fréquence d'un son audible (à 84 Hz). Cette description impliquait que Mersenne avait déjà démontré que le rapport de fréquences absolues de deux cordes vibrantes, l'une créant une première note musicale et l'autre la même note une octave au-dessus, était de 1/2. La consonance harmonique qui était perçue par l'oreille à l'écoute de ces deux notes ne pouvait s'expliquer que si le rapport des fréquences d'oscillation de l'air était lui aussi de 1/2. L'histoire de cette découverte, qui est le fruit des réflexions antérieures menées sur le sujet, dont certaines remontent à Pythagore (550 av. J.-C.), s'entrelace donc avec le développement des lois de fréquences naturelles des cordes vibrantes et de l'interprétation physique des consonances musicales. Galiléi, dans ses discours mathématiques concernant deux sciences nouvelles (1638), dévoile les discussions et les explications les plus lucides données jusque là sur la notion de fréquence.
Domaines de l'acoustique
Acoustique physique
L'acoustique physique (encore appelée acoustique fondamentale ou bien acoustique théorique) détermine les principes de la génération et de la propagation des sons et en développe le formalisme mathématique. Son domaine n'est pas nécessairement limité par la pe****tion humaine ; elle s'intéresse aussi bien aux ultrasons et infrasons, qui obéissent aux mêmes lois physiques.
L'acoustique théorique a de nombreux domaines d'application spécialisés.
L'acoustique architecturale étudie la propagation des sons dans les salles et les bâtiments y compris l'isolation phonique.
L'électroacoustique étudie spécialement les transducteurs électroacoustiques (microphones, haut-parleurs, hydrophones).
La vibroacoustique (encore appelée acoustique des structures) étudie les ondes mécaniques dans les structures et comment celles-ci interagissent et rayonnent dans les fluides environnants.
La thermoacoustique, se basant sur l'effet thermoacoustique, étudie la conversion de chaleur en énergie acoustique et vice-versa.
L'imagerie médicale utilise pour les échographies, les échographies Doppler, les techniques chirurgicales par ultrasons focalisés de haute intensité, des applications acoustiques des ultrasons.
L'acoustique non linéaire étudie les cas où les écarts à la linéarité postulée dans les équations de l'acoustique générale sont trop importants pour qu'on puisse, comme dans le cas général, les négliger.
Le contrôle non destructif utilise les résultats de l'acoustique non linéaire pour caractériser l'état d'intégrité et la « santé » de structures ou de matériaux, sans les dégrader, soit au cours de la production, soit en cours d'utilisation, soit dans le cadre de maintenance.
L'acoustique sous-marine étudie la propagation du son dans l'eau et l'interaction des ondes mécaniques constituant le son avec l'eau et les frontières avec d'autres milieux.
L'aéroacoustique étudie la génération d'un bruit par un écoulement turbulent (ex : turbulence d’un jet libre), ou interagissant avec une surface (profil d’aile, pales de rotor d’un hélicoptère, roues de compresseur ou de turbine, cavité, ...).
Acoustique humaine
L'audition détaille la physiologie de l'oreille (oreille externe, moyenne et interne) et explique les mécanismes de la pe****tion des sons par l'ouïe, et mesure la sensibilité acoustique des individus.
La psychoacoustique étudie comment les sons captés par le système auditif sont interprétés par le cerveau humain.
La phonétique acoustique se consacre notamment à l’aspect physique des sons produits par l'appareil phonatoire humain, débouchant sur les systèmes de reconnaissance automatique de la parole et de synthèse vocale.
Domaines transversaux

L’acoustique musicale s'intéresse à la production et à la pe****tion des sons musicaux.
L'instrumentation et la métrologie acoustiques.
L’acoustique environnementale se préoccupe des nuisances sonores. L'acoustique des transports (maritime, ferroviaire, aérien et automobile) s'intéresse aux questions relatives au domaine de l'acoustique intérieure des véhicules ainsi que la réduction des bruits extérieurs dus à leur circulation. L'acoustique industrielle regroupe l'ensemble des techniques servant à modifier la production et la transmission des sons et des bruits propres à l'industrie, ainsi que les techniques qui utilisent les vibrations sonores et ultrasonores à des fins d'applications mécaniques. Le contrôle du bruit s'intéresse aux solutions actives ou passives permettant d'éviter la propagation du bruit.
L'acoustique des transports (maritime, ferroviaire, aérien et automobile) s'intéresse aux questions relatives au domaine de l'acoustique intérieure des véhicules ainsi que la réduction des bruits extérieurs dus à leur circulation.
L'acoustique industrielle regroupe l'ensemble des techniques servant à modifier la production et la transmission des sons et des bruits propres à l'industrie, ainsi que les techniques qui utilisent les vibrations sonores et ultrasonores à des fins d'applications mécaniques.
Le contrôle du bruit s'intéresse aux solutions actives ou passives permettant d'éviter la propagation du bruit.
Acoustique théorique
Domaine d'étude
L'acoustique théorique détermine les principes de la génération et de la propagation des sons et en développe le formalisme mathématique. Comme la physique théorique, elle constitue un champ d'études intermédiaire entre l'acoustique expérimentale et les mathématiques, au développement desquelles elle a également contribué.
La théorie ondulatoire des phénomènes acoustiques constitue la pierre angulaire de l'acoustique théorique. Elle démontre notamment que la propagation des sons satisfait l'équation des ondes, et s'intéresse aux hypothèses effectuées afin de délimiter son domaine de validité : on distingue par exemple l'acoustique linéaire d'un fluide parfait, de l'acoustique linéaire d'un fluide dissipatif, de l'acoustique linéaire d'un solide ou encore de l'acoustique non linéaire qui s'attache à étudier les effets non linéaires dans la propagation des sons.
L'acoustique théorique s'intéresse aussi à l'étude d'autres phénomènes en relation avec la propagation des ondes acoustiques, tels que la réflexion, la transmission, la diffusion et la diffraction de celles-ci. D'autres thématiques étudiées dans le cadre de l'acoustique théorique sont les sources acoustiques (type, directivité), l'étude des fonctions de Green associées à un problème acoustique déterminé, la formulation intégrale des champs acoustiques (intégrale de Kirchhoff-Helmholtz, extension du principe de Huygens pour les ondes acoustiques, intégrale de Rayleigh), les circuits acoustiques et les guides d'onde acoustiques.
Lois fondamentales de l'acoustique
Milieu fluide
Les trois lois fondamentales de l'acoustique en milieu fluide sont l'équation d'Euler, l'équation de conservation de la masse et l'équation d'état (thermodynamique) du fluide. Ce système d'équations met en relation les paramètres caractérisant le fluide, tels que la pression, la masse volumique et la vitesse. Lorsque ce système d'équation est manipulé afin d'éliminer deux des trois paramètres mentionnés précédemment, on aboutit à l'équation des ondes, qui régit la propagation du son en milieu fluide.
Équation d'Euler
L'équation d'Euler s'obtient en appliquant le principe fondamental de la dynamique à un volume élémentaire de fluide. Son expression est la suivante (en l'absence de sources de force extérieure) :
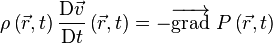
Dans cette équation, , et désignent respectivement les champs de la masse volumique, de la vitesse et de la pression associées au fluide, à la position repérée par le vecteur position , à l'instant . Il est à noter que ces grandeurs dénotent les grandeurs totales considérées : par exemple est la somme de la pression qui existerait sans l'existence d'une onde acoustique (qui est généralement prise égale à la pression statique ) et d'une fluctuation de pression due à l'onde acoustique : . L'équation d'Euler utilise une description eulérienne pour le fluide, utilisant des variables et attachées au point géométrique du référentiel considéré ; elle n'utilise pas la description lagrangienne, utilisant des variables liées à une particule du fluide suivie dans son mouvement. La notation désigne la dérivée particulaire ou dérivée totale, attachée à une particule suivie dans son mouvement, par opposition à la dérivée en un point géométrique fixe du référentiel ou dérivée locale, notée .
Conservation de la masse
L'équation de conservation de la masse s'écrit (équation valide en l'absence de sources de débit) :
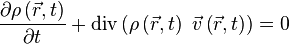 ou encore
ou encore 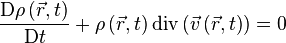
Loi de compressibilité du fluide
Quatre variables thermodynamiques permettent de caractériser le fluide : la pression , la température , le volume (ou bien la masse volumique ) et l'entropie . Les différentielles associées à ces grandeurs sont respectivement notées , , ( ou bien ), et .
Il est possible de démontrer l'identité thermodynamique suivante :
![\mathrm dS = \frac{c_V}{Tp\beta} \left[ \mathrm dP - \frac{1}{\rho \chi_S} \mathrm d \rho \right]](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/8536d4a579842bfc94e6aebb445ffb88.png)
où désigne la capacité calorifique massique à volume constant, le coefficient d'augmentation de pression isochore ()et le coefficient de compressibilité adiabatique ().
Les transformations acoustiques peuvent généralement être considérées comme adiabatiques ( dans l'équation précédente) dans le cas où le fluide est supposé ne pas être le siège d'effets dissipatifs (viscosité, transferts thermiques et phénomènes de relaxation moléculaire négligeables). Cela conduit à la loi suivante caractérisant la compressibilité du fluide (valide uniquement en l'absence de sources de chaleur) :
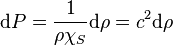 avec
avec 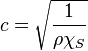
La grandeur  est homogène à une vitesse.
est homogène à une vitesse.
Équation de propagation
Il est possible de manipuler le système d'équations précédent (équation d'Euler, équation de conservation de la masse, et loi de compressibilité du fluide) afin d'obtenir une équation ne faisant intervenir que la pression . Les autres paramètres (vitesse et masse volumique) peuvent être obtenus en reportant la pression dans l'une quelconque des équations précédentes. L'équation suivante est obtenue pour la pression :
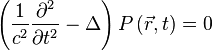
Cette équation est appelée équation d'onde, équation de d'Alembert, ou encore parfois équation de propagation. Elle est valide en dehors des sources, dans l'hypothèse où le fluide est homogène (ses caractéristiques thermodynamiques sont indépendantes du point considéré) et invariant (ses caractéristiques thermodynamiques sont indépendantes du temps).
En appliquant l'opérateur divergence sur l'équation d'Euler et l'opérateur de dérivée totale sur l'équation de conservation de la masse, après avoir divisé préalablement ces deux équations par la masse volumique, les équations suivantes sont obtenues :
En utilisant la loi de compressibilité du fluide, et en tenant compte du fait que les opérateurs divergence et dérivée totale sont commutables, la deuxième équation devient :
Finalement, en retranchant la première équation de la deuxième équation modifiée, il s'ensuit que :
Si le fluide est supposé homogène et invariant, les termes en 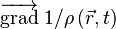 et en
et en 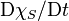 peuvent être considérés comme négligeables dans l'équation précédente. L'équation de propagation obtenue pour la pression est donc :
peuvent être considérés comme négligeables dans l'équation précédente. L'équation de propagation obtenue pour la pression est donc :
-
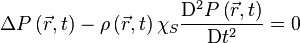 , soit finalement :
, soit finalement :
-
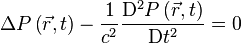 où
où 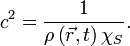
Milieu solide
La loi fondamentale caractérisant le déplacement au sein d'un solide est donnée par l'équation de Navier :
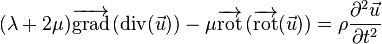
où et sont les coefficients de Lamé et le champ des déformations. Via le théorème de Helmholtz-Hodge, il est alors possible de décomposer cette équation en deux équations d'ondes :
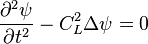
correspondant à la propagation des ondes longitudinales et
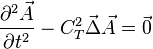
correspondant à la propagation des ondes transversales.
Dans les deux équations ci-dessus, 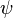 représente le potentiel scalaire de la déformation due à l'onde longitudinale et
représente le potentiel scalaire de la déformation due à l'onde longitudinale et 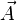 le vecteur potentiel de la déformation due à l'onde transversale. Donc contrairement au cas du fluide, il existe deux types d'ondes acoustiques pour un matériau solide. Ces deux ondes se propagent à des vitesses distinctes, ce phénomène s'expliquant par la différence entre les interactions des atomes du solide pour une onde de cisaillement et pour une onde de compression-traction. Ces ondes sont plus connues sous le nom d'onde élastiques.
le vecteur potentiel de la déformation due à l'onde transversale. Donc contrairement au cas du fluide, il existe deux types d'ondes acoustiques pour un matériau solide. Ces deux ondes se propagent à des vitesses distinctes, ce phénomène s'expliquant par la différence entre les interactions des atomes du solide pour une onde de cisaillement et pour une onde de compression-traction. Ces ondes sont plus connues sous le nom d'onde élastiques.
Démonstration En posant la vitesse de propagation des ondes longitudinales et la vitesse de propagation des ondes transversales, l'équation devient : Utilisons maintenant le théorème de Helmholtz-Hodge, on peut alors décomposer le champ des déformations : avec et . Nous avons ainsi séparé la déformation due à l'onde longitudinale () de celle due à l'onde transversale (). Il vient alors et , avec le potentiel scalaire de la déformation due à l'onde longitudinale et le vecteur potentiel de la déformation due à l'onde transversale. Comme seul le rotationnel de nous intéresse, nous fixerons arbitrairement . En réinjectant la décomposition du champ des déformations dans l'équation de Navier, on obtient : En utilisant les propriétés des composantes du champ des déformations : L'unicité de la décomposition d'Helmholtz nous donne : donc donc Les solutions recherchées ne dépendent pas des fonctions et , nous les fixerons donc à 0. Et finalement nous obtenons les équations des ondes régissant les propagations des ondes longitudinale et transversale dans un solide isotrope :
Anatomie - physiologie
L'oreille est un organe très particulier, et l'ouïe est considérée comme le plus fin des sens. L'acoustique explore donc la physiologie, qui va du pavillon de l'oreille jusqu'aux corrélations synaptiques dans le cerveau, et la psychoacoustique les interprétations de ces pe****tions au niveau cortical et cérébral. On peut définir l'acoustique par la propagation dans l'air d'un son constitué par un mouvement d'air rapide qui vient à l'oreille humaine.
Propagation - Acoustique des salles
En appliquant la théorie de la propagation des ondes aux vibrations sonores, on touche à un domaine déjà fort bien maîtrisé depuis l'Antiquité, celui de l'acoustique des salles. Pour amplifier un son, les Grecs se servaient des propriétés physiques des matériaux, de la connaissance qu'ils avaient acquise sur les phénomènes de résorption et de réfraction des sons, et construisaient des amphithéâtres en leur donnant une forme particulière. Ainsi, les constructions où devaient se produire des orateurs ou des musiciens avaient une acoustique très étudiée. Le théâtre d'Épidaure en Grèce est le témoin de l'avancement des connaissances en acoustique dès l'Antiquité.
Les connaissances en acoustique des salles au temps de la Grèce antique étaient cependant avant tout empiriques. Ce domaine de connaissance restera très longtemps presque entièrement basée sur l'expérience, se développant par suite d'essais aboutissant parfois à des échecs, parfois à de grandes réussites pouvant ensuite servir de modèle pour les salles suivantes. Le physicien américain Wallace Clement Sabine est généralement considéré comme le père de l'acoustique des salles en tant que domaine scientifique. C'est en 1900 qu'il publie l'article Reverberation qui pose les bases de cette science toute jeune.
Nuisances et pollution sonores
Nuisances : Les phénomènes de couplage vibro-acoustique sont très présents dans les industries aéronautiques, automobiles, ferroviaires et dans les industries mécaniques en général. Les problèmes liés à l'amélioration du confort intérieur et à la réduction des nuisances externes s'y posent de façon cruciale. Des problèmes similaires se posent aussi dans l'industrie du bâtiment où les cloisons et les façades d'immeuble doivent être convenablement dimensionnées de façon à réduire la transmission du bruit. L'ingénieur acousticien doit être capable d'appréhender et de modéliser les phénomènes physiques mis en jeu. Il doit acquérir les connaissances nécessaires pour mettre en œuvre à la fois des méthodes analytiques et des outils numériques pour rechercher des solutions d'amélioration des produits en termes de réduction des nuisances sonores.
Pollutions : Selon le dictionnaire français du vocabulaire normalisé de l'environnement, on peut parler de « pollution » sonore quand les conséquences du son propagé dans l'environnement génèrent une « altération » du fonctionnement de l'écosystème, généralement à la suite de la disparition ou du recul de certaines espèces, qui ne remplissent donc plus leurs fonctions écosystémiques.
Voir aussi : Isolation phonique
Facture instrumentale
Jusqu'au dix-neuvième siècle, la fabrication des instruments de musique est l'affaire d'artisans qui font appel à un savoir faire qui doit peu aux modèles scientifiques, bien que les théoriciens de la musique rattachent les principes de leur art à ceux de la physique.
Les sons instrumentaux, stables et répétables, se prêtant le mieux aux expériences scientifiques, les instruments qui les produisent, soit à partir de la vibration de cordes, soit à partir de celle d'une colonne d'air, vont servir à l'établissement des modèles physiques sur lesquels se construit l'acoustique.
De l'étude des modes de vibration des cordes et colonnes d'air qui donnent la note, l'acoustique musicale est passée à celle des couplages qui transmettent l'énergie emmagasinée dans la partie vibrante à l'air, afin de créer le son. Le volume sonore de l'instrument dépend de ce couplage. Pour des instruments à cordes frappées ou pincées, ce couplage détermine la durée pendant laquelle une note peut tenir. L'énergie est emmagasinée dans la corde au moment de l'attaque, et plus on transfère de puissance à l'air, plus la vibration faiblit vite. On étudie donc l'impédance acoustique des éléments et les transferts d'énergie entre eux. Pour les instruments à cordes : violon, guitare, piano..., ce sont principalement les caisses de résonance ; pour les instruments à vent : flûte, pipeau, trompette ... ce sont les extrémités libres des tuyaux. Ces couplages ont aussi un rôle important dans la compréhension des caractéristiques du timbre des instruments.
Enfin, la qualité musicale des instruments attire l'attention de chercheurs, qui à partir de modèles de préférences de musiciens, examinent les possibilités d'utiliser de nouveaux matériaux et de nouvelles technologies pour la fabrication d'instruments et la synthèse de leur son.
Institutions
La Société Française d'Acoustique (SFA), association de type "loi de 1901" fondée en 1948 par Yves Rocard, regroupe des acousticiens francophones, praticiens et universitaires. Son but est de favoriser la circulation des informations scientifiques et techniques entre les différents acteurs de l'acoustique ainsi que les contacts entre les laboratoires de recherche et les industriels. Elle est structurée en deux sections régionales et neuf groupes spécialisés. Elle organise tous les deux ans un Congrès Français d'Acoustique.
声学是研究媒质中机械波(包括声波、超声波和次声波)的科学,研究范围包括声波的产生,接收,转换和声波的各种效应。同时声学测量技术是一种重要的测量技术,有着广泛的应用。
最简单的声学就是声音的产生和传播,这也是声学研究的基础。
声音是由物体振动产生的。
声音的传播需要介质,它可在气体、液体和固体中传播,但真空不能传声。声音在不同物质中的传播速度也是不同的,一般在固体中传播的速度最快,液体次之,在气体中传播得最慢。并且,在气体中传播的速度还与气体的温度和压强有关。
有规律的悦耳声音叫乐音,没有规律的刺耳声音叫噪音。 响度、音调和音色是决定乐音特征的三个因素。
响度。物理学中把人耳能感觉到的声音的强弱称为响度。声音的响度大小一般与声源振动的幅度有关,振动幅度越大,响度越大。分贝(dB)则长用来表示声音的强弱。
音调。物理学中把声音的高、低称为音调。声音的音调高低一般与发生体振动快慢有关,物体振动频率越大,音调就越高。
音色。音色又叫音品,它反映了声音的品质和特色。不同物体发出的声音,其音色是不同的,因此我们才能分辨不同人讲话的声音、不同乐器演奏的声音等。
另外,有许多声音是正常人的耳朵听不到的。因为声波的频率范围很宽,由10Hz到10Hz,但正常人的耳朵只能听到20Hz到20000Hz之间的声音。通常把高于20000Hz的声音称为超声波,低于20Hz的声音称为次声波,在20Hz到20000Hz之间的声音称为可闻声。
声学分支
依据研究方法可分为: 物理声学(波动声学) 几何声学(射线声学) 统计声学
物理声学(波动声学)
几何声学(射线声学)
统计声学
依据研究对象可分为: 电声学 次声学 超声学 噪声学 量子声学 非线性声学
电声学
次声学
超声学
噪声学
量子声学
非线性声学
依据应用范围: 大气声学 水声学 生物声学(医疗声学) 语言声学 心理声学
大气声学
水声学
生物声学(医疗声学)
语言声学
心理声学

 词典释义:
词典释义:
 工作者,声
工作者,声

 〉助听器技师
〉助听器技师
 调整助听器。(《世界报》)
调整助听器。(《世界报》) 〉演出场所音响专
〉演出场所音响专

 靠音响专
靠音响专 的建议与研究建起来的。(《快报》)
的建议与研究建起来的。(《快报》) ;
; ,作曲
,作曲 ;
; 者,物理
者,物理
 ;
;
 ;
; ;
; ;
; ,行
,行 ,能手;
,能手;