En mathématiques, et plus précisément en logique mathématique, le forcing est une technique inventée par Paul Cohen pour prouver des résultats de cohérence et d'indépendance en théorie des ensembles. Elle a été utilisée pour la première fois en 1962 pour prouver l'indépendance de l'hypothèse du continu vis-à-vis de la théorie ZFC. Combinée avec la technique des modèles de permutation de Fraenkel-Mostowski-Specker (de), elle a permis également d'établir l'indépendance de l'axiome du choix relativement à ZF. Le forcing a été notablement remanié et simplifié dans les années soixante et s'est révélé être une technique extrêmement puissante, à la fois en théorie des ensembles et dans d'autres branches de la logique mathématique, comme la théorie des modèles ou la logique intuitionniste.

Motivations intuitives

Le forcing est équivalent à la méthode des modèles à valeurs booléennes (en), qui est parfois ressentie comme plus naturelle et intuitive, mais qui est en général plus difficile à appliquer.

Intuitivement, le forcing consiste à étendre l'univers V. Dans cet univers plus large, V*, on pourra par exemple avoir de nombreux nouveaux sous-ensembles de ω = {0,1,2,…} qui n'existaient pas dans l'univers V, violant ainsi l'hypothèse du continu. A priori impossible, cette construction ne fait que refléter l'un des « paradoxes » de Cantor concernant l'infini, et en particulier le fait qu'il existe des modèles dénombrables de ZFC, contenant pourtant des ensembles non dénombrables (au sens du modèle), d'après le théorème de Löwenheim-Skolem. En principe, on pourrait par exemple considérer V ∗ = V × { 0 , 1 } {\displaystyle V^{*}=V\times \{0,1\}} , identifier x ∈ V {\displaystyle x\in V} avec ( x , 0 ) {\displaystyle (x,0)} , et introduire une relation d'appartenance étendue mettant en jeu les « nouveaux » ensembles de la forme ( x , 1 ) {\displaystyle (x,1)} . Le forcing est une version élaborée de cette idée, réduisant l'expansion à l'existence d'un nouvel ensemble, et permettant un contrôle fin des propriétés de l'univers ainsi étendu.

La technique initialement définie par Cohen, connue à présent sous le nom de forcing ramifié (en), est légèrement différente du forcing non ramifié qui sera exposé ici.

Ensembles de conditions de forcing

Un ensemble partiellement ordonné de conditions de forcing, abrégé ici en ensemble de conditions, est un triplet (P, ≤, 1), où « ≤ » est un préordre sur P, et où 1 est un élément maximal, c'est-à-dire que p ≤ 1 pour tous les p de P. Les éléments de P sont appelés des conditions. On lit p ≤ q comme « p est plus forte que q » (ou encore « p raffine q »).

Intuitivement, les conditions « plus petites » fournissent davantage d'informations, tout comme l'intervalle plus étroit [3.1415926,3.1415927] fournit davantage d'informations sur le nombre π que ne le fait l'intervalle [3.1,3.2].

Associés à un ensemble de conditions donné P, on définit les P-noms, qui sont les ensembles de la forme {(u,p):u est un P-nom et p ∈ {\displaystyle \in } P}. Cette définition est circulaire, ce qui, dans ce contexte, veut dire qu'il s'agit en réalité d'une définition par récurrence transfinie ; une formulation rigoureuse consisterait par exemple à définir :

Nom(0) = {};

Nom(α + 1) = l'ensemble des sous-ensembles de (Nom(α) × P);

Nom(λ) = ∪ {\displaystyle \cup } {Nom(α) : α < λ}, si λ est un ordinal limite,

et alors la classe des P-noms est définie comme étant

V = ${\displaystyle \cup }$ {Nom(α) : α est un ordinal}.

Les P-noms constituent une extension de l'univers : étant donné x dans V, on définit xˇ comme étant le P-nom {(yˇ,1) : y ${\displaystyle \in }$ x}. Là encore, il s'agit en fait d'une définition par récurrence transfinie.

Ėtant donné un sous-ensemble quelconque G de P, on définit ensuite, toujours par récurrence transfinie, l'application d'interprétation (ou de valuation) sur les noms par val(u, G) = {val(v, G) : ∃ p ∈ G , (v, p) ∈ u}. Remarquons que si 1 est dans G, alors val(xˇ, G) = x. On définit enfin G = {(pˇ, p) : p ∈ G}, et alors val(G,G) = G.

Un bon exemple d'ensemble de conditions de forcing est (Bor(I) , ⊆ , I ), où I = [0,1] et Bor(I) sont les sous-ensembles boréliens de I de mesure de Lebesgue non nulle. Dans ce cas, on peut interpréter les conditions comme étant des probabilités, et un Bor(I)-nom définit l'appartenance en un sens probabiliste. Cet exemple permettant une visualisation assez intuitive, le langage des probabilités est parfois utilisé également avec d'autres ensembles de conditions de forcing.

Modèles transitifs dénombrables et filtres génériques

L'étape clé de la technique du forcing est, étant donné un univers V de ZFC, de déterminer un G approprié qui ne soit pas dans V. La classe de toutes les interprétations des P-noms s'avèrera être un modèle de ZFC, et une extension propre du V initial, puisque G∉V.

Plutôt que de travailler avec V, on considère un modèle transitif dénombrable M, avec (P,≤,1) ∈ M. M est ici un modèle de la théorie des ensembles, soit de tout ZFC, soit d'un sous-ensemble fini des axiomes de ZFC, ou encore d'une variante. La transitivité signifie que si x ∈ y ∈ M, alors x ∈ M ; le lemme de contraction de Mostowski dit qu'on peut supposer la transitivité de M si la relation d'appartenance est bien fondée. La transitivité permet de traiter l'appartenance et les autres propriétés élémentaires des ensembles de manière intuitive dans M. Enfin, il est toujours possible de prendre des modèles dénombrables, grâce au théorème de Löwenheim-Skolem.

M étant un ensemble, il y a des ensembles non dans M (c'est le paradoxe de Russell). L'ensemble G approprié, qu'on choisit d'adjoindre à M, doit être un filtre générique sur P, c'est-à-dire un sous-ensemble de P tel que

1 ∈ G ;

si p ≥ q ∈ G, alors p ∈ G ;

si p,q ∈ G, alors ∃r ∈ G, r ≤ p et r ≤ q ;

ce qui fait de G un filtre ; la condition pour que G soit générique est

si D ∈ M est un sous-ensemble dense de P (c'est-à-dire, si p ∈ P implique ∃q ∈ D, q ≤ p) alors G∩D ≠ 0 .

L'existence d'un filtre générique G non dans M découle du lemme de Rasiowa-Sikorski (en). En fait, on a un résultat légèrement plus fort : étant donnée une condition p ∈ P, il existe un filtre générique G tel que p ∈ G.

Si P n'a qu'un ensemble dénombrable de sous-ensembles denses, on peut en fait choisir G ∈ M ; c'est le cas trivial. Les éléments minimaux de P donnent aussi des G triviaux ; en effet si D est dense et si p est minimal, alors, comme le seul element q ≤ p est p lui-même, p ∈ D. Ainsi, tout filtre contenant un élément minimal est générique, et l'on peut encore choisir G ∈ M.

Forcing

Étant donné un filtre générique G⊆P, la construction du nouveau modèle par forcing est la suivante. La sous-classe des P-noms dans M est notée M. Soit M[G]={val(u,G):u∈M}. Pour ramener l'étude de la théorie des ensembles de M[G] à celle de M, on travaille dans le langage du forcing, qui est celui du calcul des prédicats du premier ordre avec l'appartenance comme relation binaire et tous les noms comme constantes.

Définissons alors p ${\displaystyle \Vdash }$ φ(u₁,…,u_n) (qui se lit « p force φ ») où p est une condition, φ est une formule du langage du forcing, et les u_i sont des noms, comme signifiant que si G est un filtre générique contenant p, alors M[G] ⊨ φ(val(u₁,G),…,val(u_n,G)). Le cas particulier 1 ${\displaystyle \Vdash }$ φ est souvent noté P ${\displaystyle \Vdash }$ φ ou ${\displaystyle \Vdash }$ φ. Ces assertions sont vraies dans M[G] quel que soit le choix de G.

L'important est que cette définition « externe » de la relation de forcing p ${\displaystyle \Vdash }$ φ est équivalente à une définition « interne », par récurrence transfinie sur les noms pour les occurrences de u ∈ v et de u = v, suivie d'une récurrence ordinaire sur la complexité des formules. Cela a pour conséquence que toutes les propriétés de M[G] sont en fait des propriétés de M, et la vérification dans M[G] des axiomes de ZFC en devient élémentaire. On résume généralement cela par les trois propriétés suivantes :

Vérité : M[G] ⊨ φ(val(u1,G),…,val(un,G)) si et seulement si pour une certaine condition p ∈ G, p ⊩ {\displaystyle \Vdash } φ(u1,…,un) (la formule φ est forcée par G).

Définissabilité : L'assertion « p ⊩ {\displaystyle \Vdash } φ(u1,…,un) » est définissable dans M.

Cohérence : si p ⊩ {\displaystyle \Vdash } φ(u1,…,un) et q ≤ p, alors q ⊩ {\displaystyle \Vdash } φ(u1,…,un).

On peut résumer ce qui précède en disant que le résultat fondamental de cohérence est qu'étant donné un ensemble de conditions P, on peut supposer qu'il existe un filtre générique G, non dans l'univers V, tel que V[G] est encore un univers, donc un modèle de ZFC. De plus, les assertions vraies dans V[G] se ramènent à des assertions vraies dans V par rapport à la relation de forcing.

Les deux styles, soit l'adjonction de G à un modèle transitif dénombrable M, soit à l'univers entier V, sont fréquemment employés. On rencontre moins souvent l'approche utilisant la définition « interne » du forcing, sans mentionner de modèles. Cette dernière méthode est celle qu'avait utilisée Cohen initialement, et qui est devenue la méthode de l'analyse des valeurs booléennes.

Le forcing de Cohen

L'ensemble de conditions (non trivial) le plus simple est (Fin(ω,2), ⊇, 0), l'ensemble des fonctions définies sur une partie finie de ω à valeur dans 2={0,1}, ordonné par l'inclusion inverse, c'est-à-dire qu'une condition p peut être vue comme formée de deux sous-ensembles finis disjoints de ω, p[1] et p[0], que l'on peut voir comme les parties « oui » et « non » de p, aucune information n'étant donnée sur le complémentaire de ces sous-ensembles. Dire que q est plus forte que p signifie que q ⊇ p, autrement dit que les parties « oui » et « non » de q contiennent celles de p, donc donnent à ce sens davantage d'informations.

Soit G un filtre générique pour cet ensemble de conditions. Si p et q appartiennent à G, p∪q est également une condition, puisque G est un filtre. Cela veut dire que g=⋃G est fonctionnelle, car deux conditions de G ont les mêmes valeurs sur l'intersection de leurs domaines.

g est en fait une fonction partout définie sur ω : étant donné n ∈ ω, soit D_n={ p : p(n) est défini }, alors D_n est dense (car pour un p tel que n ne soit pas dans le domaine de p, en adjoignant une valeur quelconque pour n, le résultat sera dans D_n). Une condition p ∈ G∩D_n a n dans son domaine, et comme p ⊆ g, g(n) est défini.

Soit X=g[1], l'ensemble des réponses « oui » des conditions génériques. On peut déterminer un nom pour X directement. Soit X = { (nˇ, p) : p(n)=1 } ; on a donc val(X, G) = X. Supposons alors que A⊆ω soit dans V. Nous allons montrer que X≠A. Soit D_A = { p : ∃n, n∈dom(p) et p(n)=1 si et seulement si n∉A }. D_A est dense (en effet, étant donné p, si n n'est pas dans le domaine de p, il suffit d'adjoindre pour n une valeur opposée à celle de « n∈A »). Ainsi, tout p∈G∩D_A force X≠A. En résumé, X est un nouveau sous-ensemble de ω, nécessairement infini.

La même construction, où ω est remplacé par ω×ω₂, c'est-à-dire qu'on considère des fonctions définies sur un sous-ensemble fini de couples de la forme (n,α), avec n<ω et α<ω₂, et ayant pour valeurs 0 ou 1, aboutit à créer ω₂ nouveaux sous-ensembles de ω. Ces sous-ensembles sont tous distincts, par un argument de densité : étant donné α<β<ω₂, soit D_α,β={p:∃n, p(n,α)≠p(n,β)} ; alors chaque D_α,β est dense, et une condition générique dans cet ensemble prouve qu'il y a un entier qui distingue le α-ème nouvel ensemble du β-ème, c'est-à-dire qu'il appartient à l'un des deux, mais pas à l'autre.

Ceci ne suffit pas à falsifier l'hypothèse du continu, car il faut encore montrer qu'on n'a pas créé de nouvelles applications qui seraient des bijections entre ω et ω₁, ou entre ω₁ et ω₂. Ainsi, si l'on avait pris comme ensemble de conditions Fin(ω,ω₁) (les applications allant des parties finies de ω vers ω₁), on aurait dans V[G] une bijection de ω vers ω₁, et donc ω₁ serait devenu un ordinal dénombrable dans V[G] (on dit dans ce cas que ω₁ s'est effondré).

C'est pourquoi la dernière étape dans la démonstration de l'indépendance de l'hypothèse du continu est de montrer que le forcing de Cohen n'effondre pas les cardinaux. Cette démonstration utilise une propriété combinatoire pour montrer que toutes les antichaînes de cet ensemble de conditions sont dénombrables, comme on le verra dans la section suivante.

La condition de chaîne dénombrable

Deux éléments p et q de P sont dits incompatibles (ce qu'on note p ⊥ q) s'il n'y a pas de r dans P tel que r ≤ p et r ≤ q (en particulier, on n'a ni p ≤ q, ni q ≤ p).

Une antichaîne forte (en) de P (appelée simplement antichaîne dans ce contexte) est un sous-ensemble A dont toutes les paires sont incompatibles (en particulier, A est une antichaîne au sens faible). Dans l'exemple des ensembles boréliens, l'incompatibilité de p et q signifie que p∩q est de mesure nulle. Dans l'exemple des applications de domaine fini, l'incompatibilité signifie que p∪q n'est pas une fonction, c'est-à-dire que p et q prennent deux valeurs différentes au même point.

On dit que P satisfait à la condition de chaîne dénombrable si toute antichaîne de P est dénombrable. On voit facilement que Bor(I) satisfait la condition de chaîne dénombrable, parce que la somme des mesures ne peut dépasser 1. Il en est de même de Fin(E,2) pour tout ensemble E infini, mais la démonstration en est plus difficile.

Ce qui justifie l'importance des antichaînes dans le forcing, c'est que pour la plupart des applications, ensembles denses et antichaînes maximales sont équivalents. Une antichaîne maximale A (pour l'inclusion) est une antichaîne telle que tout élément p ∈ P est compatible avec au moins un élément de A (toute antichaîne est contenue dans une antichaîne maximale, d'après le lemme de Zorn). Étant donnée une antichaîne maximale A, soit D = {p : il existe q∈A, p≤q}. D est dense, et G∩D≠0 si et seulement si G∩A≠0. Réciproquement, étant donné un sous-ensemble dense D, le lemme de Zorn montre qu'il existe une antichaîne maximale A⊆D, et alors G∩D≠0 si et seulement si G∩A≠0.

Supposons alors que P satisfasse la condition de chaîne dénombrable. Étant donnés x et y ∈ V, avec f:x→y dans V[G], on peut approximer f dans V de la manière suivante : soit u un P-nom pour f (il en existe un par définition de V[G]) et p une condition qui force u à être une fonction de x vers y. On définit une fonction F dont le domaine est x par F(a) = { b : ∃ q ≤ p, q force u(aˇ) = bˇ }. D'après la propriété de définissabilité, cette définition a un sens dans V. Par cohérence du forcing, des b différents viennent de p incompatibles. D'après la condition de chaîne dénombrable, F(a) est donc dénombrable.

En résumé, f est « inconnue » dans V, puisqu'elle dépend de G, mais pas complètement pour un forcing satisfaisant à la condition de chaîne dénombrable : en effet, on peut alors identifier un ensemble dénombrable d'hypothèses sur la valeur de f en n'importe quelle entrée, indépendamment de G.

Il en découle la très importante conséquence suivante : si dans V[G], f:α→β est une surjection d'un ordinal infini vers un autre, une surjection analogue existe dans V. En particulier, les cardinaux ne peuvent s'effondrer ; la conclusion est que 2 ≥ ℵ₂ dans V[G] ; la même construction permet en fait d'affecter à 2 « presque » n'importe quelle valeur comme on le verra dans la section suivante.

Le forcing d'Easton

La valeur exacte de 2 dans le modèle de Cohen, ainsi que dans des variantes telles que Fin(ω × κ , 2) pour des cardinaux κ quelconques, fut déterminée par Robert M. Solovay, qui montra également comment construire des modèles où l'hypothèse du continu généralisée est fausse pour un nombre fini de cardinaux réguliers. Ainsi, dans le modèle de Cohen, si 2 = ℵ1 est vrai dans V, alors 2 = ℵ2 est vrai dans V[G].

En 1970, William Bigelow Easton (de) montra comment violer l'hypothèse du continu généralisée pour un nombre infini, et même une classe propre, de cardinaux réguliers, démontrant que les restrictions connues sur les valeurs des puissances des cardinaux réguliers (monotonie, théorème de Cantor et théorème de König) étaient les seules prouvables dans ZFC.

Ce travail introduisit l'idée du forcing avec une classe propre de conditions. En général, cette technique échoue à construire un modèle de ZFC. Par exemple, Fin (ω × On , 2), où « On » est la classe de tous les ordinaux, fait du continu une classe propre. Fin (ω , On) permet une énumération (dénombrable) des ordinaux. Dans les deux cas, le V[G] qui en résulte n'est clairement pas un modèle de ZFC.

À cette époque, on pensait que des méthodes de forcing plus sophistiquées permettraient de même de construire des valeurs arbitraires des puissances des cardinaux singuliers. Mais le problème s'est avéré difficile, avec l'apparition de nouvelles restrictions démontrables dans ZFC, et les modèles obtenus par forcing dépendant parfois de divers axiomes de grands cardinaux ; il reste encore de nombreuses questions ouvertes.

Réels aléatoires

Dans l'exemple des ensembles boréliens (Bor(I) , ⊆ , I), un filtre générique donné converge vers un nombre réel r, dont on dit que c'est un réel aléatoire. Un P-nom pour le développement décimal de r (au sens de l'ensemble canonique d'intervalles décimaux convergeant vers r) peut être donné en posant r = { ( Eˇ , E ) : E = [ k⋅10 , (k+1)⋅10 ], 0≤k<10 }. En un sens, ceci est simplement un sous-nom de G.

Pour retrouver G à partir de r, on prend les boréliens de I « contenant » r. Comme l'ensemble de conditions est dans V, mais que ce n'est pas le cas de r, cela est à proprement parler impossible. Mais il est en un certain sens naturel de dire que l'intervalle [.5,.6] de V « contient » un réel aléatoire dont le développement décimal commence par .5. Ceci se formalise grâce à la notion de « code borélien ».

Tout borélien peut être construit en partant d'intervalles à extrémités rationnelles et en prenant les opérations de complémentaire et d'union dénombrable, ce un nombre dénombrable de fois (cette construction n'étant pas unique). La liste de ces opérations est appelé un code borélien. Étant donné un borélien B dans V, on en détermine un code, et on applique la même séquence de construction dans V[G], obtenant un borélien B*, dont on démontre qu'il ne dépend pas du code choisi, et que ses propriétés élémentaires sont les mêmes, par exemple, que si B⊆C, alors B*⊆C*, ou que si B est de mesure nulle, il en est de même de B*.

Ainsi, étant donné un réel aléatoire r, on peut montrer que G = { B (dans V) : r∈B* (dans V[G]) }. Cette équivalence amène généralement à écrire V[r] au lieu de V[G].

Une interprétation différente des réels de V[G] a été donnée par Dana Scott. Les rationnels de V[G] ont des noms qui correspondent à un ensemble dénombrable de valeurs rationnelles distinctes associées à une antichaîne de boréliens, ou, en d'autres termes, à une certaine fonction à valeurs rationnelles sur I = [0,1]. Les réels de V[G] correspondent alors à des coupures de Dedekind de telles fonctions, autrement dit, à des fonctions mesurables.

Modèles à valeurs booléennes

La méthode du forcing peut peut-être s'expliquer plus clairement en termes de modèles à valeurs booléennes. Dans ces modèles, chaque assertion se voit attribuer une valeur de vérité choisie dans une algèbre de Boole infinie, plutôt que simplement l'une des deux valeurs « vrai » ou « faux ». On choisit ensuite un ultrafiltre sur cette algèbre, le passage au quotient par cet ultrafiltre donne des valeurs vrai/faux aux assertions. La théorie résultante possède un modèle contenant cet ultrafiltre, que l'on peut interpréter comme un modèle étendant le modèle de départ. En choisissant ce dernier, et l'ultrafiltre, de manière appropriée, on peut obtenir les propriétés voulues, car en un sens, seules les assertions qui doivent être vraies (qui sont « forcées » d'être vraies) le seront, par la propriété d'extension minimale.

Une interprétation métamathématique

Par le forcing, on cherche usuellement à montrer qu'une assertion donnée est cohérente avec ZFC (ou parfois avec une certaine extension de ZFC). Une façon d'interpréter cet argument est de supposer ZFC cohérente, et de l'utiliser pour démontrer la cohérence de ZFC + cette assertion.

Chaque condition de forcing est un ensemble fini d'informations, l'idée étant que seuls ces ensembles finis sont pertinents pour des démonstrations de cohérence, puisque d'après le théorème de compacité, une théorie possède un modèle si chaque sous-ensemble fini de ses axiomes en a un. On peut donc choisir un ensemble infini de conditions pour étendre un modèle de la théorie des ensembles, il suffit de vérifier la cohérence condition par condition, puis, déduire de la cohérence de la théorie des ensembles, la cohérence de la théorie étendue par cet ensemble infini de conditions.

在数学学科集合论中，力迫是 保罗·寇恩（Paul J. Cohen）发明的一种技术，用来证明与策梅洛-弗兰克尔公理有关的一致性和独立性结果。它在1962年首次被用来证明连续统假设和选择公理对策梅洛-弗兰克尔集合论的独立性。实际上在寇恩正式引入力迫法前，它已经被广泛地应用于递归论中。寇恩的力迫法最初是创建在分歧分层（ramified hierarchy）上，难于理解。1960年代通过索罗维（Solovay）与斯科特（Scott）等人的努力力迫法被相当程度的重做和简化。

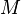力迫法大致是一种扩张模型的方法。给定一个模型以及模型内一个偏序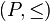，通过构造通集（generic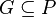）来实现模型的扩张。因为通集不在内，所以这是一个真正的扩张。记为。它有以下性质：

对于中所有元素，都可以在中找到一个对应的元素，即所谓的名（name）。

存在一个可定义的关系成为力迫()使得对于任何一个命题，满足当且仅当存在使得。即中的满足关系是可以在中定义的即使这种定义具有非常强的非一致性（它严重地依赖参数p）。

2是非常重要的一条性质。它说明力迫法对于模型的扩张是“非常小的”。扩张的模型牢牢地被原来的模型控制住，使得我们能够通过原来的模型获得扩张模型的大量的信息。在数学技巧上例如它使得我们能够对扩张模型的基数是否仍然保持住做强有力推断。

索罗维后来对力迫法进行了非常深入地研究。他（与Tennenbaum）引入了迭代力迫并用有限支撑迭代力迫证明了苏斯林猜想（Suslin hypothesis）。勒维（Laver）引入可数支撑迭代力迫证明了波雷尔猜想（Borel's conjecture），从而导致了正常力迫（proper forcing）的引入。现在力迫法已经成为集合论中不可缺少的工具。而且通过乌丁（Woodin）等人的工作，力迫的意义也远远不仅是集合论的一项工具。

选择 可数 相关

可数

相关

外延

无穷

配对

幂集

正则性

并集

马丁公理

公理模式 替代 分类

替代

分类

笛卡儿积

德摩根定律

交集

幂集

补集

对称差

并集

概念

方法

势

基数（大基数）

类

可构造全集

连续统假设

对角论证法

元素 有序对 多元组

有序对

多元组

集合族

力迫

一一对应

序数

超限归纳法

文氏图

可数集

空集

有限集合（继承有限集合）

模糊集

无限集合

递归集合

子集

传递集合

不可数集

泛集

可替代的集合论

集合论

朴素集合论

康托尔定理

策梅洛 广义

广义

数学原理 新基础

新基础

策梅洛-弗兰克 冯诺伊曼-博内斯-哥德尔 Morse–Kelley 克里普克–普拉特克 塔斯基–格罗滕迪克

冯诺伊曼-博内斯-哥德尔 Morse–Kelley

Morse–Kelley

克里普克–普拉特克

塔斯基–格罗滕迪克

悖论

问题

罗素悖论

萨斯林问题

亚伯拉罕·弗兰克尔

伯特兰·罗素

恩斯特·策梅洛

格奥尔格·康托尔

约翰·冯·诺伊曼

库尔特·哥德尔

卢菲特·泽德

保尔·贝尔奈斯

保罗·寇恩

理乍得·戴德金

托马斯·耶赫

威拉德·蒯因