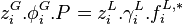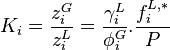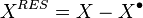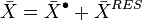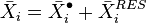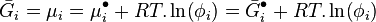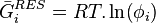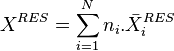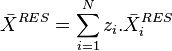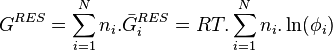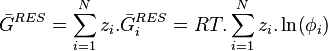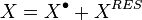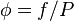En thermodynamique, la fugacité d'une espèce chimique exprime l'écart entre les propriétés de cette espèce pure ou dans un mélange réel et les propriétés de cette même espèce à l'état de gaz parfait pur. La notion de fugacité est applicable à toutes les phases (gaz, liquide, solide), elle permet notamment le calcul des équilibres de phases.
À la suite de l'apparition de l'équation d'état de van der Waals en 1873, il devenait possible de calculer les équilibres de phases gaz-liquide. En effet, cette équation novatrice pour son époque permettait de calculer aussi bien les propriétés d'un gaz que celles d'un liquide. Willard Gibbs et Pierre Duhem introduisirent peu après (1875 à 1878) la notion de potentiel chimique, notion importante dans les équilibres de phases et les équilibres chimiques. Toutefois, la notion de potentiel chimique se révéla difficile à manipuler, car un potentiel chimique ne peut être calculé qu'à une constante additive près et non de façon absolue, de plus le potentiel chimique de toute espèce tend vers moins l'infini à dilution infinie. En 1900 et 1901, Gilbert Lewis introduisit la notion de fugacité qui décrit l'écart de comportement d'un corps réel, pur ou en mélange, par rapport au même corps à l'état de gaz parfait pur. À partir de la fugacité, Lewis introduisit plus tard (1923) la notion d'activité chimique plus spécialement employée pour les phases condensées (liquide ou solide).
Les coefficients de fugacité sont calculés avec des équations d'état, ils sont également en théorie applicables à toutes les phases, mais dans la pratique leur usage est généralement restreint aux gaz ; les phases liquide et solide sont le plus souvent représentées par des activités chimiques. Les grandeurs résiduelles, calculées à partir des coefficients de fugacité, expriment l'écart entre les grandeurs extensives d'un mélange réel (gazeux, liquide ou solide) et celles d'un mélange de gaz parfaits.
Définitions
Fugacité
La variation isotherme à composition constante du potentiel chimique d'un corps i pur ou en mélange en fonction de la pression est donnée par la relation :
-
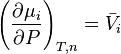
avec le volume molaire du corps pur ou le volume molaire partiel du corps i en mélange.
Pour un gaz parfait pur, le volume molaire vaut :
-
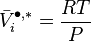
En conséquence, la variation isotherme du potentiel chimique d'un gaz parfait pur vaut :
-
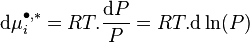
Lewis s'inspira de cette relation pour introduire la notion de fugacité d'un corps i, notée 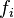 , qu'il définit ainsi :
, qu'il définit ainsi :
Variation isotherme du potentiel chimique : 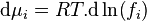 |
La fugacité a la dimension d'une pression.
Pour un corps à l'état de gaz parfait en mélange la fugacité est égale à la pression partielle de ce corps : . Pour un gaz parfait pur, la fugacité est bien entendu égale à la pression : .
En revanche pour un mélange réel la fugacité d'un corps présent dans ce mélange n'est pas égale à sa pression partielle : 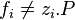 . Pour un corps pur la fugacité n'est pas égale à la pression :
. Pour un corps pur la fugacité n'est pas égale à la pression : 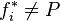 .
.
La fugacité se définit pour n'importe quelle phase, aussi bien pour un gaz que pour un liquide, un solide ou un fluide supercritique.
Coefficient de fugacité
L'intégration à pression et température constantes de l'expression définissant la fugacité donne la relation entre le potentiel chimique 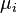 du corps i dans un mélange réel et le potentiel chimique
du corps i dans un mélange réel et le potentiel chimique 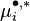 du même corps i pur à l'état de gaz parfait aux mêmes pression et température :
du même corps i pur à l'état de gaz parfait aux mêmes pression et température :
-
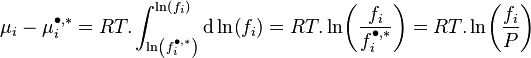
Le théorème de Gibbs conduit à la relation suivante :
-
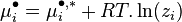
entre le potentiel chimique 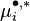 du corps i pur à l'état de gaz parfait et le potentiel chimique
du corps i pur à l'état de gaz parfait et le potentiel chimique 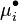 du même corps dans un mélange de gaz parfaits à la même composition que le mélange réel,
du même corps dans un mélange de gaz parfaits à la même composition que le mélange réel, 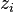 étant la fraction molaire du corps i dans le mélange réel, les deux potentiels étant définis aux mêmes pression et température que le mélange réel. Nous avons donc la relation :
étant la fraction molaire du corps i dans le mélange réel, les deux potentiels étant définis aux mêmes pression et température que le mélange réel. Nous avons donc la relation :
-
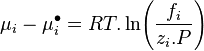
dans laquelle les deux potentiels chimiques sont définis aux mêmes pression, température et composition. Cette relation montre que le potentiel chimique d'un corps i dans un mélange de gaz parfaits est égale à la pression partielle de ce corps :
-
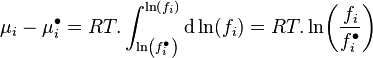
-
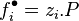
Pour tout corps i du mélange, le rapport entre la fugacité réelle et la fugacité du gaz parfait en mélange aux mêmes pression, température et composition est appelé coefficient de fugacité, il est noté 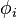 :
:
Coefficient de fugacité : 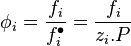 |
Le coefficient de fugacité est adimensionnel.
Le coefficient de fugacité exprime l'écart entre le potentiel chimique 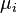 d'un corps i dans un mélange réel et le potentiel chimique
d'un corps i dans un mélange réel et le potentiel chimique 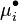 de ce même corps i en mélange de gaz parfaits aux mêmes pression, température et composition que le mélange réel :
de ce même corps i en mélange de gaz parfaits aux mêmes pression, température et composition que le mélange réel :
-
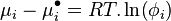
Le coefficient de fugacité exprime également l'écart entre le potentiel chimique 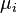 d'un corps i dans un mélange réel et le potentiel chimique
d'un corps i dans un mélange réel et le potentiel chimique 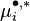 de ce même corps i à l'état de gaz parfait pur, aux mêmes pression et température :
de ce même corps i à l'état de gaz parfait pur, aux mêmes pression et température :
-
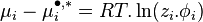
Par définition, le coefficient de fugacité d'un gaz parfait en mélange est donc égal à 1 :
Pour un gaz parfait : 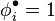 et
et 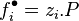
A fortiori pour un gaz parfait pur :
Pour un gaz parfait pur : 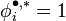 et
et 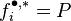
Le gaz parfait correspond au cas idéal dans lequel les molécules n'ont aucune interaction entre elles hormis des chocs élastiques.
Lorsque les molécules s'attirent, la pression réelle est inférieure à celle du gaz parfait correspondant de même composition, à la même température et dans le même volume : dans ce cas 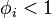 et
et 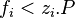 .
.
Inversement, lorsque les molécules se repoussent, la pression réelle est supérieure à celle du gaz parfait correspondant de même composition, à la même température et dans le même volume : dans ce cas 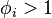 et
et 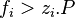 .
.
Calcul du coefficient de fugacité
Contrairement au potentiel chimique qui n'est toujours défini qu'à une constante additive près, le coefficient de fugacité peut être calculé de façon absolue, ce qui le rend particulièrement intéressant dans le calcul des propriétés des mélanges réels. Si ce calcul est en théorie possible pour toutes les phases (gaz, liquide, solide), il est en pratique utilisé pour les phases gazeuses à toutes les pressions et pour les phases liquides aux hautes pressions (plus de 10 atm) : il nécessite en effet une équation d'état, or il n'en existe pas à l'heure actuelle représentant convenablement les phases condensées, du moins à basse pression (moins de 10 atm).
Avec une équation d'état explicite en pression
Avec une équation d'état dans laquelle la pression P est exprimée explicitement en fonction du volume V, de la température T et de la composition (nombre de moles ), , telle que les (en)équations d'état de van der Waals, Soave-Redlich-Kwong, Peng-Robinson, le coefficient de fugacité se calcule selon :
![RT.\ln \! \left( \phi_i \right) = - \int_{+\infty}^{V} \left[ \left( \frac{\partial P}{\partial n_i} \right)_{V,T,n_{j \neq i}} - \frac{RT}{V} \right]. \mathrm dV - RT . \ln Z](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/82c91e79c0905fdf335ed00bd414aea8.png)
![\ln \! \left( \phi_i \right) = - \int_{+\infty}^{V} \left[ n.\left( \frac{\partial Z}{\partial n_i} \right)_{V,T,n_{j \neq i}} + Z - 1 \right]. \frac{\mathrm dV}{V} - \ln Z](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/8965c39dfcea06e9055e6a84110ab733.png)
avec :
, dérivée partielle de la pression par rapport à la quantité du corps i, à volume, température et quantités des corps j autres que i constants ;
, le nombre de moles du corps i dans le mélange ;
, nombre de moles total dans le mélange ;
, volume molaire du mélange réel ;
, facteur de compressibilité du mélange réel.
On vérifie que pour un gaz parfait, le volume molaire valant 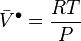 , le facteur de compressibilité est constant
, le facteur de compressibilité est constant 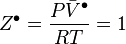 , d'où
, d'où 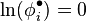 et le coefficient de fugacité
et le coefficient de fugacité 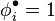 .
.
Démonstration
Soit un mélange de 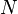 constituants à pression P, température T et volume V, chaque constituant i étant représenté par
constituants à pression P, température T et volume V, chaque constituant i étant représenté par 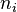 moles, le mélange étant en une seule phase (gaz, liquide ou solide).
moles, le mélange étant en une seule phase (gaz, liquide ou solide).
Le coefficient de fugacité de tout constituant i est défini par la relation :
-
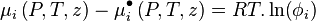
Pour le mélange réel, le potentiel chimique peut indifféremment s'écrire en fonction des variables réelles :
-
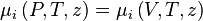
Pour le mélange de gaz parfaits correspondant, il n'en va pas de même, car à P, T et composition du mélange réel le volume correspondant est calculé selon :
-
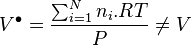
d'où la relation :
-
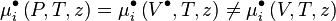
La variation isotherme du potentiel chimique de tout constituant i en fonction du volume est donnée par :
-
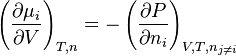
En intégrant cette relation entre un volume 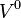 quelconque et le volume
quelconque et le volume 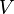 du mélange, à température et composition constantes, on obtient :
du mélange, à température et composition constantes, on obtient :
-
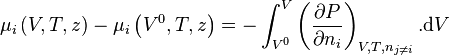
Pour un mélange de gaz parfaits en particulier, pour tout corps i, on a :
-
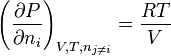
d'où les relations entre potentiels chimiques du constituant i à l'état de gaz parfait :
-
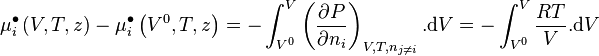
-
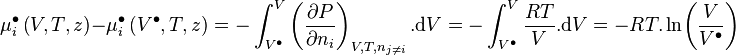
Dans cette dernière relation on identifie :
-
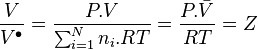
avec 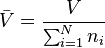 le volume molaire du mélange réel et
le volume molaire du mélange réel et 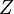 le facteur de compressibilité du mélange réel.
le facteur de compressibilité du mélange réel.
Nous pouvons écrire :
-
![\mu_i \left( V,T,z \right) - \mu_i \left( V^0,T,z \right)
+ \mu_i^{\bullet} \left( V^0,T,z \right) \underbrace{- \mu_i^{\bullet} \left( V,T,z \right)
+ \mu_i^{\bullet} \left( V,T,z \right)}_{=0} - \mu_i^{\bullet} \left( V^{\bullet},T,z \right)
= - \int_{V^0}^{V} \left[ \left( \frac{\partial P}{\partial n_i} \right)_{V,T,n_{j \neq i}} - \frac{RT}{V} \right]. \mathrm d V - RT.\ln Z](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/bc6ae456ad7be5fa9e8ba900b6122c34.png)
Lorsque le volume tend vers l'infini (lorsque la pression tend vers 0), le comportement du mélange réel à température et composition (nombre de moles) constantes tend vers celui du mélange de gaz parfaits, aussi peut-on écrire :
-
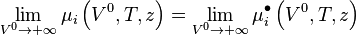
d'où :
-
![\mu_i \left( V,T,z \right) - \mu_i^{\bullet} \left( V^{\bullet},T,z \right)
= - \int_{+\infty}^{V} \left[ \left( \frac{\partial P}{\partial n_i} \right)_{V,T,n_{j \neq i}} - \frac{RT}{V} \right]. \mathrm d V - RT.\ln Z](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/1f3486fcc6397f3ddabbea3c5efe6bbb.png)
or par définition :
-
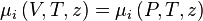
-
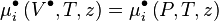
-
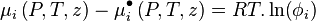
d'où :
![RT.\ln \! \left( \phi_i \right) = - \int_{+\infty}^{V} \left[ \left( \frac{\partial P}{\partial n_i} \right)_{V,T,n_{j \neq i}} - \frac{RT}{V} \right]. \mathrm dV - RT . \ln Z](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/82c91e79c0905fdf335ed00bd414aea8.png)
En divisant les expressions par 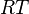 (il est possible de l'extraire de l'intégrale puisque la température est constante dans toutes les expressions) et dans l'intégrale en factorisant par
(il est possible de l'extraire de l'intégrale puisque la température est constante dans toutes les expressions) et dans l'intégrale en factorisant par 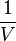 :
:
-
![\ln \! \left( \phi_i \right) = - \int_{+\infty}^{V} \left[ \left( \frac{\partial P}{\partial n_i} \right)_{V,T,n_{j \neq i}}.\frac{V}{RT} - 1 \right]. \frac{\mathrm dV}{V} - \ln Z](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/114f0e4135018bde6417b50344571ae0.png)
Étant donné que la dérivée partielle de la pression est considérée à volume et température constants, on peut écrire :
-
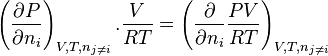
Avec 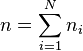 la quantité de matière totale dans le mélange, et
la quantité de matière totale dans le mélange, et 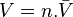 , on a :
, on a :
-
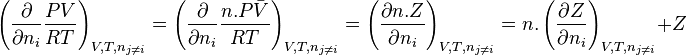
d'où :
![\ln \! \left( \phi_i \right) = - \int_{+\infty}^{V} \left[ n.\left( \frac{\partial Z}{\partial n_i} \right)_{V,T,n_{j \neq i}} + Z - 1 \right]. \frac{\mathrm dV}{V} - \ln Z](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/8965c39dfcea06e9055e6a84110ab733.png)
Avec une équation d'état explicite en volume
Avec une équation d'état dans laquelle le volume V est exprimé explicitement en fonction de la pression P, de la température T et de la composition (nombre de moles ), , comme pour certaines formes de l'équation du viriel, le coefficient de fugacité se calcule selon :
![RT.\ln \! \left( \phi_i \right) = \int_{0}^{P} \left[ \bar V_i - \frac{RT}{P} \right]. \mathrm dP](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/b9939c4c55a13fe08f8589601e78ac2c.png)
![\ln \! \left( \phi_i \right) = \int_{0}^{P} \left[ n . \left( \frac{\partial Z}{\partial n_i} \right)_{P,T,n_{j \neq i}} + Z - 1 \right]. \frac{\mathrm dP}{P}](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/ac7f81f1bbc5980d30415766c2515dfe.png)
avec :
, volume molaire partiel du corps i dans le mélange réel ;
, le nombre de moles du corps i dans le mélange ;
, nombre de moles total dans le mélange ;
, volume molaire du mélange réel ;
, facteur de compressibilité du mélange réel.
On vérifie que pour un gaz parfait, le volume molaire valant 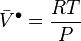 , le facteur de compressibilité est constant
, le facteur de compressibilité est constant 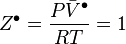 , d'où
, d'où 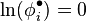 et le coefficient de fugacité
et le coefficient de fugacité 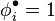 .
.
Démonstration
Soit un mélange de 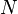 constituants à pression P, température T et volume V, chaque constituant i étant représenté par
constituants à pression P, température T et volume V, chaque constituant i étant représenté par 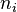 moles, le mélange étant en une seule phase (gaz, liquide ou solide).
moles, le mélange étant en une seule phase (gaz, liquide ou solide).
La variation isotherme du potentiel chimique de tout constituant i en fonction de la pression est donnée par :
-
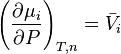
avec le volume molaire partiel du constituant i :
-
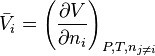
En intégrant cette relation entre une pression 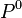 quelconque et la pression
quelconque et la pression 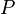 du mélange, à température et composition constantes, on obtient :
du mélange, à température et composition constantes, on obtient :
-
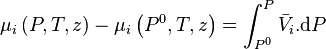
Pour un mélange de gaz parfaits en particulier, le volume molaire partiel de tout corps i vaut :
-
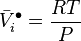
d'où la relation entre potentiels chimiques du constituant i à l'état de gaz parfait :
-
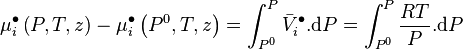
En soustrayant l'expression obtenue pour les gaz parfaits à l'expression générale obtenue précédemment, nous avons :
-
![\mu_i \left( P,T,z \right) - \mu_i \left( P^0,T,z \right) + \mu_i^{\bullet} \left( P^0,T,z \right) - \mu_i^{\bullet} \left( P,T,z \right) = \int_{P^0}^{P} \left[ \bar V_i - \frac{RT}{P} \right]. \mathrm d P](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/878272cc3d530b33ecc85ebbd9b638fb.png)
Lorsque la pression tend vers 0, le comportement du mélange réel à température et composition constantes tend vers celui du mélange de gaz parfaits, aussi peut-on écrire :
-
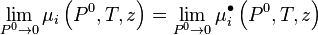
d'où :
-
![\mu_i \left( P,T,z \right) - \mu_i^{\bullet} \left( P,T,z \right) = \int_{0}^{P} \left[ \bar V_i - \frac{RT}{P} \right]. \mathrm d P](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/5e6fbf811e3761f98bec0626ed46019d.png)
or par définition :
-
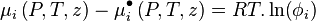
d'où :
![RT.\ln \! \left( \phi_i \right) = \int_{0}^{P} \left[ \bar V_i - \frac{RT}{P} \right]. \mathrm dP](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/b9939c4c55a13fe08f8589601e78ac2c.png)
En divisant les expressions par 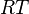 (il est possible de l'extraire de l'intégrale puisque la température est constante dans toutes les expressions) et dans l'intégrale en factorisant par
(il est possible de l'extraire de l'intégrale puisque la température est constante dans toutes les expressions) et dans l'intégrale en factorisant par 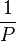 :
:
-
![\ln \! \left( \phi_i \right) = \int_{0}^{P} \left[ \bar V_i .\frac{P}{RT} - 1 \right]. \frac{\mathrm dP}{P}](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/9368c26ce5f51bef7f9a48ea12b92f8c.png)
Étant donné que la dérivée partielle du volume est considérée à pression et température constantes, on peut écrire :
-
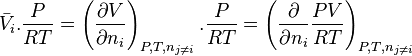
Avec 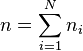 la quantité de matière totale dans le mélange, et
la quantité de matière totale dans le mélange, et 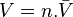 , on a :
, on a :
-
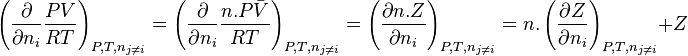
d'où :
![\ln \! \left( \phi_i \right) = \int_{0}^{P} \left[ n . \left( \frac{\partial Z}{\partial n_i} \right)_{P,T,n_{j \neq i}} + Z - 1 \right]. \frac{\mathrm dP}{P}](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/ac7f81f1bbc5980d30415766c2515dfe.png)
Équilibre de phases
Relation générale
Lorsque deux phases ou plus (gaz, liquide, solide) sont en équilibre, les potentiels chimiques de chacun des corps en présence sont homogènes sur l'ensemble des phases. Autrement dit, s'il existe à l'équilibre les phases , les potentiels chimiques de tout corps i présent répondent à l'égalité :
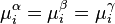
En introduisant les fugacités respectives 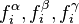 de tout corps i dans chacune de ces phases, on peut écrire pour chacun des potentiels chimiques :
de tout corps i dans chacune de ces phases, on peut écrire pour chacun des potentiels chimiques :
-
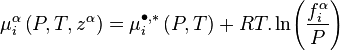
-
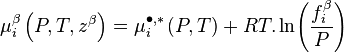
-
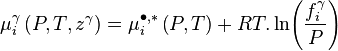
Le potentiel chimique du corps pur à l'état de gaz parfait 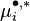 est le même dans toutes ces expressions, puisque la pression et la température sont les mêmes dans toutes les phases à l'équilibre. L'égalité des potentiels chimiques du corps i dans l'ensemble des phases à l'équilibre conduit à la condition d'équilibre des phases :
est le même dans toutes ces expressions, puisque la pression et la température sont les mêmes dans toutes les phases à l'équilibre. L'égalité des potentiels chimiques du corps i dans l'ensemble des phases à l'équilibre conduit à la condition d'équilibre des phases :
Condition d'équilibre des phases : 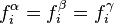 |
En termes de condition d'équilibre des phases, l'égalité des fugacités est tout à fait équivalente à l'égalité des potentiels chimiques : si l'une est vérifiée, l'autre est aussi vérifiée.
Les équilibre de phases sont le plus souvent calculées selon deux approches : l'approche 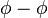 (phi-phi) et l'approche
(phi-phi) et l'approche 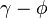 (gamma-phi). L'approche
(gamma-phi). L'approche 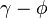 nécessite deux modèles distincts : une équation d'état pour la phase vapeur et un modèle de coefficient d'activité pour la phase liquide ; elle est recommandée pour des pressions inférieures à 10 bar. Au-delà, l'approche
nécessite deux modèles distincts : une équation d'état pour la phase vapeur et un modèle de coefficient d'activité pour la phase liquide ; elle est recommandée pour des pressions inférieures à 10 bar. Au-delà, l'approche 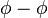 est recommandée car elle ne nécessite qu'une seule et même équation d'état pour représenter les deux phases, ce qui rend le calcul cohérent à l'approche du point critique où les deux phases doivent se rejoindre. Les deux modèles de l'approche
est recommandée car elle ne nécessite qu'une seule et même équation d'état pour représenter les deux phases, ce qui rend le calcul cohérent à l'approche du point critique où les deux phases doivent se rejoindre. Les deux modèles de l'approche 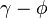 posent des problèmes de convergence numérique autour du point critique.
posent des problèmes de convergence numérique autour du point critique.
Approche ϕ - ϕ
Dans un équilibre liquide-vapeur, les fugacités des deux phases 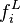 et
et 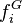 peuvent être calculées à partir d'une même équation d'état (par exemple l'équation d'état cubique de Soave-Redlich-Kwong ou Peng-Robinson) : cette approche est alors appelée « approche
peuvent être calculées à partir d'une même équation d'état (par exemple l'équation d'état cubique de Soave-Redlich-Kwong ou Peng-Robinson) : cette approche est alors appelée « approche 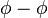 » (phi-phi). En introduisant les fractions molaires respectives
» (phi-phi). En introduisant les fractions molaires respectives 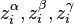 et les coefficients de fugacité respectifs
et les coefficients de fugacité respectifs 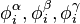 de tout corps i dans chacune des phases à l'équilibre, on peut écrire pour chacune des fugacités :
de tout corps i dans chacune des phases à l'équilibre, on peut écrire pour chacune des fugacités :
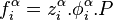
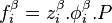
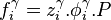
L'égalité des fugacités du corps i dans l'ensemble des phases à l'équilibre conduit à l'expression de l'approche 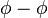 (phi-phi) :
(phi-phi) :
Approche 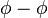 : : 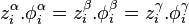 |
On déduit également de cette expression le coefficient de partage, noté , du corps i entre les phases et :
Coefficient de partage : 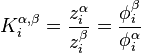
On peut de même établir des coefficients de partage entre toutes les autres phases.
Approche γ - ϕ
Comme évoqué plus haut, il n'existe pas à l'heure actuelle d'équation d'état représentant convenablement les phases liquides, notamment aux basses pressions (moins de 10 atm) : il est alors préférable pour calculer les fugacités des phases liquides d'employer un modèle de coefficient d'activité et l'approche dite « approche » (gamma-phi) pour le calcul de l'équilibre de phases.
Pour la phase vapeur, en introduisant le coefficient de fugacité en phase vapeur, l'expression de la fugacité en phase vapeur est :
Fugacité en phase vapeur : 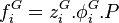
Pour la phase liquide, en introduisant le coefficient d'activité 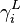 en phase liquide et la fugacité
en phase liquide et la fugacité 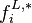 du corps pur en phase liquide, l'expression de la fugacité en phase liquide est :
du corps pur en phase liquide, l'expression de la fugacité en phase liquide est :
Fugacité en phase liquide : 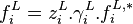
L'égalité des fugacités à l'équilibre des phases 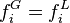 induit l'expression de l'approche
induit l'expression de l'approche 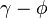 (gamma-phi) :
(gamma-phi) :
Approche 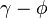 : : 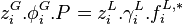 |
On déduit également de cette expression le coefficient de partage du corps i entre les deux phases, noté :
Coefficient de partage : 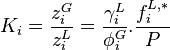
Cette approche est développée dans l'article Activité chimique. Elle conduit, pour des solutions idéales :
à la loi de Raoult par la convention symétrique ;
à la loi de Henry par la convention dissymétrique.
Grandeurs extensives des solutions réelles
Grandeurs résiduelles
Une grandeur résiduelle exprime l'écart entre une grandeur thermodynamique extensive d'un mélange réel et la même grandeur thermodynamique extensive d'un mélange de gaz parfaits aux mêmes pression, température et composition :
Grandeur résiduelle : 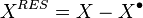 |
Une grandeur résiduelle est par construction également une grandeur extensive, il est donc possible de définir une grandeur molaire résiduelle pour le mélange et une grandeur molaire partielle résiduelle pour chacun des corps présents dans le mélange.
Les relations suivantes sont également vraies entre grandeurs molaires et grandeurs molaires partielles, respectivement réelles, du gaz parfait et résiduelles :
-
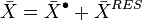
-
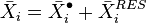
Calcul des grandeurs résiduelles
À partir des coefficients de fugacité
Pour l'enthalpie libre , l'identité des potentiels chimiques et des enthalpies libres molaires partielles permet d'écrire :
-
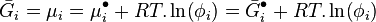
Le deuxième terme est donc l'enthalpie libre molaire partielle résiduelle :
Enthalpie libre molaire partielle résiduelle : 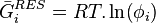
À partir de l'enthalpie libre résiduelle, toutes les autres grandeurs résiduelles peuvent être calculées :
, entropie molaire partielle résiduelle, calculée par l'une des relations de Maxwell ;
, enthalpie molaire partielle résiduelle ;
, volume molaire partiel résiduel, calculé par l'une des relations de Maxwell ;
, énergie interne molaire partielle résiduelle ;
, énergie libre molaire partielle résiduelle.
Le théorème d'Euler sur les fonctions homogènes du premier ordre s'applique aux grandeurs résiduelles puisque ce sont des grandeurs extensives, avec nombre de moles et fraction molaire de chacun des corps présents dans le mélange :
Grandeur résiduelle : 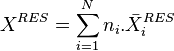 Grandeur molaire résiduelle :
Grandeur molaire résiduelle : 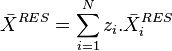
On a donc en particulier pour l'enthalpie libre :
Enthalpie libre résiduelle : 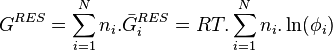 Enthalpie libre molaire résiduelle :
Enthalpie libre molaire résiduelle : 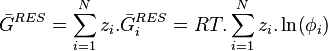
Avec une équation d'état explicite en pression
Avec une équation d'état dans laquelle la pression P est exprimée explicitement en fonction du volume V, de la température T et de la composition (nombre de moles ), , telle que les (en)équations d'état de van der Waals, Soave-Redlich-Kwong, Peng-Robinson, les grandeurs molaires résiduelles se calculent selon :
, énergie libre molaire résiduelle ;
, énergie interne molaire résiduelle ;
, entropie molaire résiduelle ;
, volume molaire résiduel ;
, enthalpie libre molaire résiduelle ;
, enthalpie molaire résiduelle ;
avec :
, volume molaire du mélange réel ;
, volume molaire du mélange de gaz parfaits aux mêmes pression, température et composition que le mélange réel, ;
, facteur de compressibilité du mélange réel.
On vérifie que pour un gaz parfait, le facteur de compressibilité étant constant 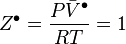 , toutes les grandeurs résiduelles sont nulles.
, toutes les grandeurs résiduelles sont nulles.
Avec une équation d'état explicite en volume
Avec une équation d'état dans laquelle le volume V est exprimé explicitement en fonction de la pression P, de la température T et de la composition (nombre de moles ), , comme pour certaines formes de l'équation du viriel, les grandeurs molaires résiduelles se calculent selon :
, enthalpie libre molaire résiduelle ;
, enthalpie molaire résiduelle ;
, entropie molaire résiduelle ;
, volume molaire résiduel ;
, énergie libre molaire résiduelle ;
, énergie interne molaire résiduelle ;
avec :
, volume molaire du mélange réel ;
, volume molaire du mélange de gaz parfaits aux mêmes pression, température et composition que le mélange réel, ;
, facteur de compressibilité du mélange réel.
On vérifie que pour un gaz parfait, le facteur de compressibilité étant constant 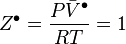 , toutes les grandeurs résiduelles sont nulles.
, toutes les grandeurs résiduelles sont nulles.
Calcul des grandeurs extensives réelles
Les grandeurs extensives du mélange de gaz parfaits peuvent être calculées facilement à l'aide des propriétés des corps purs à l'état de gaz parfait puisque selon le théorème de Gibbs le mélange de gaz parfaits est une solution idéale.
Les grandeurs extensives du mélange réel se calculent donc en appliquant la définition des grandeurs résiduelles :
Propriétés d'un mélange réel : 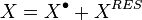 |
Rappelons que ceci est valable pour toutes les phases (gaz, liquide ou solide) pour peu que l'on dispose d'une équation d'état permettant de calculer les grandeurs résiduelles de cette phase, donc les écarts de cette phase au mélange de gaz parfaits correspondant. Dans la pratique, ceci est surtout appliqué au calcul des propriétés des gaz ; pour les phases condensées, liquide ou solide, une autre approche est préférée : la solution idéale choisie est le mélange des corps purs dans la même phase et aux mêmes pression et température que le mélange réel, les propriétés sont calculées à l'aide d'un modèle de coefficients d'activité et de grandeurs d'excès.

 词典释义:
词典释义:
 即逝
即逝


 即逝
即逝 消失
消失 , 繁
, 繁 , 大量,
, 大量,  样性;
样性; 性;
性;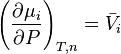
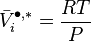
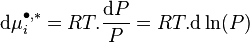
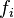 , qu'il définit ainsi
, qu'il définit ainsi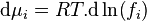
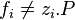 . Pour un corps pur la fugacité n'est pas égale à la pression
. Pour un corps pur la fugacité n'est pas égale à la pression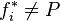 .
.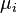 du corps
du corps 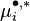 du même corps
du même corps 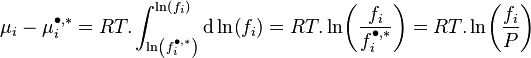
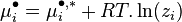
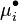 du même corps dans un mélange de gaz parfaits à la même composition que le mélange réel,
du même corps dans un mélange de gaz parfaits à la même composition que le mélange réel, 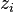 étant la fraction molaire du corps
étant la fraction molaire du corps 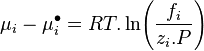
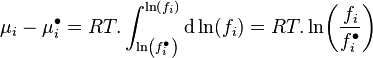
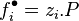
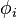
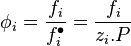
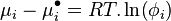
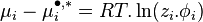
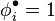 et
et 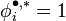 et
et 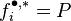
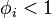 et
et 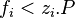 .
.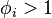 et
et 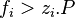 .
.![RT.\ln \! \left( \phi_i \right) = - \int_{+\infty}^{V} \left[ \left( \frac{\partial P}{\partial n_i} \right)_{V,T,n_{j \neq i}} - \frac{RT}{V} \right]. \mathrm dV - RT . \ln Z](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/82c91e79c0905fdf335ed00bd414aea8.png)
![\ln \! \left( \phi_i \right) = - \int_{+\infty}^{V} \left[ n.\left( \frac{\partial Z}{\partial n_i} \right)_{V,T,n_{j \neq i}} + Z - 1 \right]. \frac{\mathrm dV}{V} - \ln Z](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/8965c39dfcea06e9055e6a84110ab733.png)
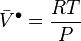 , le facteur de compressibilité est constant
, le facteur de compressibilité est constant 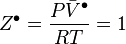 , d'où
, d'où 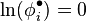 et le coefficient de fugacité
et le coefficient de fugacité 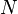 constituants à pression
constituants à pression 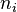 moles, le mélange étant en une seule phase (gaz, liquide ou solide).
moles, le mélange étant en une seule phase (gaz, liquide ou solide).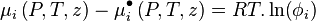
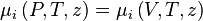
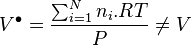
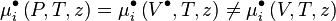
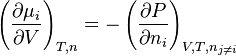
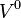 quelconque et le volume
quelconque et le volume 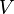 du mélange, à température et composition constantes, on obtient
du mélange, à température et composition constantes, on obtient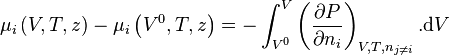
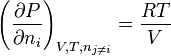
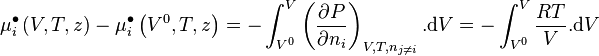
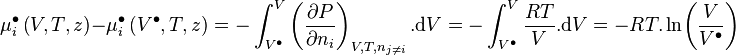
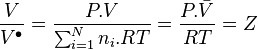
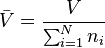 le volume molaire du mélange réel et
le volume molaire du mélange réel et 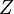 le facteur de compressibilité du mélange réel.
le facteur de compressibilité du mélange réel.![\mu_i \left( V,T,z \right) - \mu_i \left( V^0,T,z \right)
+ \mu_i^{\bullet} \left( V^0,T,z \right) \underbrace{- \mu_i^{\bullet} \left( V,T,z \right)
+ \mu_i^{\bullet} \left( V,T,z \right)}_{=0} - \mu_i^{\bullet} \left( V^{\bullet},T,z \right)
= - \int_{V^0}^{V} \left[ \left( \frac{\partial P}{\partial n_i} \right)_{V,T,n_{j \neq i}} - \frac{RT}{V} \right]. \mathrm d V - RT.\ln Z](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/bc6ae456ad7be5fa9e8ba900b6122c34.png)
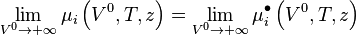
![\mu_i \left( V,T,z \right) - \mu_i^{\bullet} \left( V^{\bullet},T,z \right)
= - \int_{+\infty}^{V} \left[ \left( \frac{\partial P}{\partial n_i} \right)_{V,T,n_{j \neq i}} - \frac{RT}{V} \right]. \mathrm d V - RT.\ln Z](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/1f3486fcc6397f3ddabbea3c5efe6bbb.png)
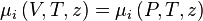
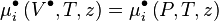
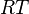 (il est possible de l'extraire de l'intégrale puisque la température est constante dans toutes les expressions) et dans l'intégrale en factorisant par
(il est possible de l'extraire de l'intégrale puisque la température est constante dans toutes les expressions) et dans l'intégrale en factorisant par 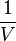
![\ln \! \left( \phi_i \right) = - \int_{+\infty}^{V} \left[ \left( \frac{\partial P}{\partial n_i} \right)_{V,T,n_{j \neq i}}.\frac{V}{RT} - 1 \right]. \frac{\mathrm dV}{V} - \ln Z](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/114f0e4135018bde6417b50344571ae0.png)
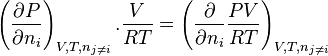
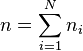 la quantité de matière totale dans le mélange, et
la quantité de matière totale dans le mélange, et 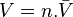 , on a
, on a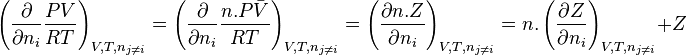
![RT.\ln \! \left( \phi_i \right) = \int_{0}^{P} \left[ \bar V_i - \frac{RT}{P} \right]. \mathrm dP](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/b9939c4c55a13fe08f8589601e78ac2c.png)
![\ln \! \left( \phi_i \right) = \int_{0}^{P} \left[ n . \left( \frac{\partial Z}{\partial n_i} \right)_{P,T,n_{j \neq i}} + Z - 1 \right]. \frac{\mathrm dP}{P}](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/ac7f81f1bbc5980d30415766c2515dfe.png)
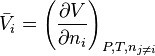
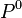 quelconque et la pression
quelconque et la pression 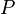 du mélange, à température et composition constantes, on obtient
du mélange, à température et composition constantes, on obtient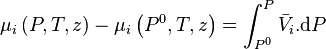
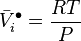
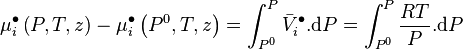
![\mu_i \left( P,T,z \right) - \mu_i \left( P^0,T,z \right) + \mu_i^{\bullet} \left( P^0,T,z \right) - \mu_i^{\bullet} \left( P,T,z \right) = \int_{P^0}^{P} \left[ \bar V_i - \frac{RT}{P} \right]. \mathrm d P](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/878272cc3d530b33ecc85ebbd9b638fb.png)
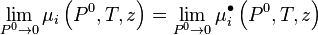
![\mu_i \left( P,T,z \right) - \mu_i^{\bullet} \left( P,T,z \right) = \int_{0}^{P} \left[ \bar V_i - \frac{RT}{P} \right]. \mathrm d P](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/5e6fbf811e3761f98bec0626ed46019d.png)
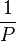
![\ln \! \left( \phi_i \right) = \int_{0}^{P} \left[ \bar V_i .\frac{P}{RT} - 1 \right]. \frac{\mathrm dP}{P}](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/9368c26ce5f51bef7f9a48ea12b92f8c.png)
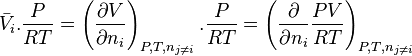
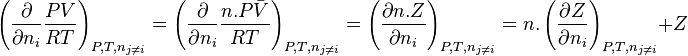
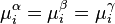
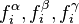 de tout corps
de tout corps 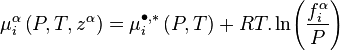
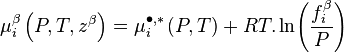
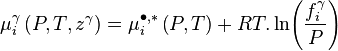
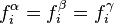
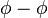 (phi-phi) et l'approche
(phi-phi) et l'approche 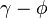 (gamma-phi). L'approche
(gamma-phi). L'approche 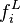 et
et 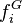 peuvent être calculées à partir d'une même équation d'état (par exemple l'équation d'état cubique de Soave-Redlich-Kwong ou Peng-Robinson)
peuvent être calculées à partir d'une même équation d'état (par exemple l'équation d'état cubique de Soave-Redlich-Kwong ou Peng-Robinson)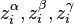 et les coefficients de fugacité respectifs
et les coefficients de fugacité respectifs 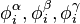 de tout corps
de tout corps 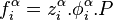
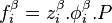
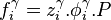
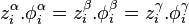
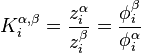
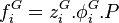
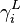 en phase liquide et la fugacité
en phase liquide et la fugacité 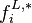 du corps pur en phase liquide, l'expression de la fugacité en phase liquide est
du corps pur en phase liquide, l'expression de la fugacité en phase liquide est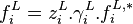
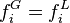 induit l'expression de l'
induit l'expression de l'