La tautologie (du grec ταὐτολογία, composé de ταὐτό, « la même chose », et λέγω, « dire » : le fait de redire la même chose) est une phrase ou un effet de style ainsi tourné que sa formulation ne puisse être que vraie. La tautologie peut aussi s'apparenter au truisme ou « lapalissade ». En logique mathématique, le mot « tautologie » désigne une proposition toujours vraie selon les règles du calcul propositionnel. On utilise aussi l'adjectif tautologique en mathématiques pour désigner des structures qui émergent naturellement de la définition de certains objets.
En logique, une tautologie est une formule valide pour toutes les assignations possibles et appartient au métalangage.
Utilisation (tautologies intentionnelles) en rhétorique
La tautologie (comme ses divers effets voisins), lorsqu'elle est intentionnelle, utilisée comme un slogan ou effet de rhétorique, vise à renforcer l'expression de la pensée. C'est le cas de beaucoup de celles qui précèdent, qu'il s'agisse de renforcer le propos (« vu, de mes yeux vu ») ou de faire rire (« Mais le mal que j'y trouve, c'est que votre père est votre père »).
C'est ainsi qu'une tautologie, parce qu'elle est vraie, peut servir à faire passer de fausses idées, en profitant de l'impression de vérité et d'évidence qu'elle dégage.
Eugène Ionesco, dans sa pièce Rhinocéros, montre ce procédé en bafouant les lois de la logique par le biais de tautologies et syllogismes fumeux mais corrects du point de vue grammatical et "mécanique" ; Jean : « J'ai de la force parce que j'ai de la force. »
Karl Marx, dans Le Capital, Livre I, « Le prix est le nom monétaire du travail réalisé dans la marchandise. L'équivalence de la marchandise et de la somme d'argent, exprimée dans son prix, est donc une tautologie, comme en général l'expression relative de valeur d'une marchandise est toujours l'expression de l'équivalence de deux marchandises. Mais si le prix comme exposant de la grandeur de valeur de la marchandise est l'exposant de son rapport d'échange avec la monnaie, il ne s'ensuit pas inversement que l'exposant de son rapport d'échange avec la monnaie soit nécessairement l'exposant de sa grandeur de valeur. »
En fait, elle peut tout aussi bien servir de mode de manipulation qu'être utilisée au second degré, comme un clin d'œil.
Exemple politique : « Votez pour le parti gagnant ! » Les slogans de ce type font omission du fait que l'on part en principe de zéro et que l'on a besoin des électeurs pour parvenir à un résultat.
Tautologies en logique mathématique
En logique mathématique, le terme a pris un sens technique qui peut s'écarter du sens commun. En calcul propositionnel, à la suite du Tractatus logico-philosophicus de Wittgenstein paru en 1921, on appelle tautologie (du calcul propositionnel) une proposition (ou énoncé) toujours vraie, c'est-à-dire vraie quelle que soit la valeur de vérité, vraie ou fausse, de ses constituants élémentaires. Dit autrement, la table de vérité de cet énoncé prend toujours la valeur vrai. Par exemple « s'il fait beau, alors il fait beau » qui est de la forme « si A, alors A » (ou « A implique A ») est une tautologie. Les tautologies ainsi définies peuvent paraître sans réelle signification, n'apporter aucune information. Si c'est bien le cas de celle précitée, les tautologies propositionnelles peuvent tout de même être bien plus complexes. Affirmer que « de A1, … , An on déduit B », revient à affirmer que la proposition « si A1, … , si An alors B » est une tautologie. Or, comme le remarque Kleene le raisonnement logique ordinaire revient à manier de telles relations de déduction (pas forcément dans le cadre du calcul propositionnel).
Il reste qu'en calcul propositionnel classique, la question de savoir si un énoncé donné est une tautologie est décidable, c'est-à-dire que cette question peut être théoriquement résolue de façon purement mécanique, par exemple par les tables de vérité. Cependant, ce problème est co-NP-complet, le temps de calcul devient rapidement prohibitif (du moins dans l'état actuel des connaissances).
En calcul des prédicats, on appelle universellement valide un énoncé (formule close) qui est vrai dans tous les modèles (où elle a un sens). Cette notion n'est pas en général décidable, la vérité ne se définit pas de façon mécanique, les modèles pouvant être infinis.
Aussi, un usage courant en logique mathématique est d'appeler tautologie du calcul des prédicats une formule close obtenue à partir d'une tautologie du calcul propositionnel en substituant aux variables propositionnelles des formules du calcul des prédicats. Par exemple, P étant un prédicat à une place, « Pour tout x P(x) implique Pour tout x P(x) » est une tautologie obtenue à partir de la tautologie propositionnelle précédente. Une telle formule est bien universellement valide, mais une formule peut être universellement valide sans être une tautologie. Par exemple « Pour tout x P(x) implique Il existe x P(x) » est universellement valide (les modèles sont supposés toujours avoir au moins un élément), mais n'est pas une tautologie. Comme les tautologies sont décidables, cela a un sens de formaliser la déduction en prenant pour axiomes toutes les tautologies du calcul des prédicats.
Objets tautologiques en mathématiques
En mathématiques, on utilise l'adjectif « tautologique » pour désigner des structures qui émergent naturellement de la définition de certains objets. Par exemple :
le fibré cotangent d'une variété différentielle se distingue de son fibré tangent en ce qu'il est naturellement muni d'une forme différentielle tautologique, dite forme de Liouville. Loin d'être anodine, l'existence d'une telle structure tautologique est très riche de conséquences, puisqu'elle est à l'origine de la formulation hamiltonienne de la mécanique classique et plus généralement de la géométrie symplectique.
le fibré tautologique (en) sur une grassmannienne G est le fibré vectoriel dont la fibre au-dessus d'un point V de G est l'espace vectoriel V. Son universalité le rend important dans l'étude des classes caractéristiques. Le fibré en droites (en) tautologique sur un espace projectif intervient en géométrie algébrique et en K-théorie.
Exemples
Tautologies qui cherchent à démontrer un autre fait non dit (implicite par la forme de phrase employée) et non vérifié, souvent pour en faire un slogan :
« La fin n'a jamais été aussi près » (si le temps possède une fin, chaque seconde qui s'écoule nous en rapproche forcément)
« 100 % de nos clients achètent nos produits. » (c'est parce qu'ils achètent les produits qu'on peut les qualifier de clients)
« 100 % des gagnants ont tenté leur chance. » (célèbre slogan publicitaire de la Française des jeux : sauf cas de fraude, chaque participant doit bien acheter un ticket pour participer au tirage)
Tautologies souvent jugées superfétatoires, qui n’apportent en fait aucune précision supplémentaire. D'un point de vue lexical, les tautologies ci-dessous sont des pléonasmes, c’est-à-dire qu'il y a redondance de l'information (emphase) :
« Monter en haut »
« Descendre en bas »
« Tourner sur le côté »
« C’est mon livre à moi. »
« Tu le lui diras toi-même. »
Tautologies involontaires, voire insoupçonnées. Ce sont des tautologies par oubli ou méconnaissance de sens ou d'origine des mots :
« Au jour d'aujourd'hui » (pour signifier « à ce jour »), « hui » venant du latin : hodie se traduisant par « ce jour », l'expression signifie finalement « au jour du jour de ce jour ». Le terme « aujourd'hui » est déjà tautologique en soi, signifiant « Au jour de ce jour ».
« Incessamment sous peu », l'adverbe « Incessamment » comme l'expression « sous peu » étant synonymes de « bientôt ».
« Huile d'olive », olive provient d'oliva, fruit de l'olivier et huile provient du latin ŏlĕum, provenant lui-même de olea venant du grec ἐλαία, elaía (« olivier, olive »).
Ces tautologies par oubli de sens sont fréquentes en toponymie. Le nom d’un lieu peut exprimer une idée dans une langue oubliée, les nouveaux locuteurs introduiront une répétition alors dans le nouveau nom :
Mont Ventoux : Ventoux veut dire « mont » dans une langue préceltique. Ce sens ayant été oublié, on a ensuite ajouté mont devant, pour bien préciser à quoi s’appliquait le terme, ce qui aboutit à une tautologie : le mont mont.
La Balme-les-Grottes : balme signifie « grotte » en vieux français.
Le mont Fujiyama : yama (kanji : 山) signifie « montagne » en japonais. L'appellation correcte est donc "le Mont Fuji" ou "le Fujisan" (kanji : 富士山) directement.
Le val d'Aran : Aran signifiait « vallée » en aquitain. Tandis que val signifie aujourd'hui également « vallée » en occitan.
Le lac de Grand-Lieu : Lieu dériverait, selon certains étymologistes, d'un mot gaulois équivalant au loc'h breton signifiant « étang côtier, lagune ».
Le lac Léman : Léman voulant dire « lac ».
Le désert de Gobi : Gobi signifie en mongol « semi-désert ».
Le désert du Sahara : Sah'ra signifie « désert » en arabe.
Le golfe du Morbihan : Mor-bihan signifie en breton « petite mer » = golfe.
Le pont d'Alcantara : Sud d'Espagne. Alcantara signifie "Le pont" en arabe.
La fête de l'Haïd : Haïd signifie "fête" en arabe.
La porte Tian'anmen : men (门/門) signifie « porte » en Chinois, ce qui signifierai la porte de la porte de la paix céleste.
Les Col de Cou : cou étant dérivé du mot col.
Expressions consacrées courantes ou proverbiales :
« Je l’ai vu de mes propres yeux. »
« Donner c'est donner reprendre c'est voler. »
« C’est la vérité pleine et entière. »
« C'est la vérité vraie ! »
«Dura lex, sed lex », c'est-à-dire « La loi est dure, mais c'est la loi ».
« Quand on voit ce qu'on voit, on a raison de penser ce qu'on pense. »
« C’est sûr et certain ! »
« Une promesse est une promesse ! »
« Un sou est un sou ! »
« Concurrence pure et parfaite » (structure de marché qui satisfait 5 conditions particulières. L'expression se justifie dans la conception classique en tant que réunion de la concurrence pure de Knight et de la concurrence parfaite d'Arrow)
« Je me présente face à vous en personne. » (Quoique le sens signifie souvent ici qu’on ne se fait pas représenter par quelqu'un d'autre ni par le truchement d'un support électronique...)
« La raison du plus fort est toujours la meilleure. » (la plus forte sous-entendant que la force prime le droit) ce qui est également une tautologie selon Pascal et Jean-Jacques Rousseau, Du Droit du plus fort.
Tautologies prononcées par des personnes célèbres :
« Lui, c'est lui, et moi c'est moi. » (dixit Laurent Fabius - à propos de François Mitterrand - lors de sa prise de fonction de Premier ministre en 1984).
« Ce qui est intolérable ne sera pas toléré. La place des délinquants n'est pas dans la rue, elle est en prison. » (Brice Hortefeux, alors ministre de l'Intérieur, vis-à-vis de faits d'insécurité ayant lieu à Grenoble en 2010).
« Appelez-ça comme vous voulez, une défaite, c'est une défaite. » (Jean-François Copé, répondant au journal télévisé à Laurence Ferrari qui cherche à faire reconnaître à l'homme politique l'échec de l'UMP aux élections sénatoriales de 2011).
« Si on n’avait pas perdu une heure et quart, on serait là depuis une heure et quart. » (Johnny Hallyday, s'adressant à son équipier lors de l'édition 2002 du Dakar).
Tautologies dans la littérature :
« Quand je danse, je danse ; quand je dors, je dors. » (Montaigne, Essais)
« Mais le mal que j'y trouve, c'est que votre père est votre père. » (Molière, L'Avare - Acte IV, Scène 1)
词典释义：
，荒唐
，荒诞
;
;
子，语
;
。
、
、
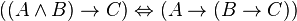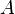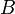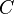分别以真或假代入，然后根据规则算出各子式的真假值，最后算出整个式子真假值：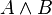
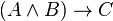
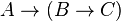
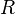为真的命题赋值情况下
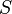也都会为真，则称
，这相当于恒真式
。
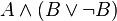，而
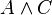。此时