Un autre, Tore and the Town in Thin Ice, est en préparation.
另外一本出版物《托尔和薄冰上的城镇》正在编写。
 词典释义:
词典释义:
n.m.1. 【建筑】状半圆线脚装饰, 柱脚圆盘线脚2. 【数学】形圆纹, 3. 【计算机】单孔铁芯
 状半圆线脚装饰, 柱脚圆盘线脚
状半圆线脚装饰, 柱脚圆盘线脚
 形圆纹
形圆纹
 ,
, 

tore m. 管 ; 圆
; 圆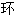

tore d'eau 给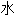
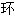
tore magnétique 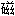 心
心
tore magnétique〔电〕磁心,磁环
tore magnétique磁心
mémoire à tores磁心存储器
tore d'eau给水环
Un autre, Tore and the Town in Thin Ice, est en préparation.
另外一本出版物《托尔和薄冰上的城镇》正在编写。

Un tore est un solide géométrique représentant un tube courbé refermé sur lui-même. Le terme « tore » comporte différentes acceptions plus spécifiques selon le contexte :
En ingénierie ou en géométrie élémentaire, un tore désigne un solide de révolution de l'espace obtenu à partir d'un cercle, ou bien sa surface. Une chambre à air, une bouée, certains joints d'étanchéité ou encore certains beignets (les donuts nord-américains) ont ainsi une forme plus ou moins torique ; En architecture, un tore correspond à une moulure ronde, semi-cylindrique, entourant le pied d'une colonne ou d'un pilier ; En mathématiques, plus particulièrement en topologie, un tore est un quotient d'un espace vectoriel réel de dimension finie par un réseau, ou tout espace topologique qui lui est homéomorphe. La surface du solide de révolution décrit ci-dessus est généralement homéomorphe à (R/Z)×(R/Z), exception faite des cas dégénérés.
Le solide de révolution en géométrie euclidienne
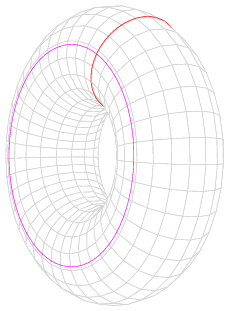
Un tore désigne le volume de l'espace euclidien R engendré par la rotation d'un cercle C de rayon r autour d'une droite affine D située dans son plan à une distance R de son centre. Dans cette acception, certains auteurs désignent par tore plein le solide obtenu, réservant le terme tore pour la surface correspondante. À l'action d'une isométrie affine directe près, le tore (plein) est uniquement déterminé par les deux paramètres réels R et r.
La forme du tore (plein) dépend du signe de R-r :
Pour R = 0, alors le tore (plein) correspondant est une boule (solide obtenu par la rotation d'un disque autour de l'un de ses diamètres). Certains auteurs réservent la dénomination tore pour R-r positif, voire strictement positif.
Si R < r, le tore est dit « croisé » et ressemble visuellement à une citrouille ; le solide est topologiquement une boule fermée de l'espace tridimensionnel, et sa surface une sphère.
Si R = r, le tore est dit « à collier nul ».
si R > r, le tore est dit « ouvert » et ressemble à une chambre à air ou encore à un beignet (donut nord-américain).
Un tore peut être défini paramétriquement par:
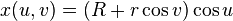
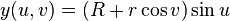
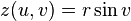
où
En sommant les carrés
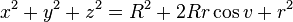
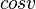 et on élève à nouveau au carré
et on élève à nouveau au carré

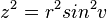 Pour obtenir finalement :
Pour obtenir finalement :

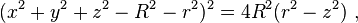
Une autre équation cartésienne pour un tore symétrique par rapport à l'axe z est
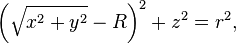
En éliminant algébriquement la racine carrée, on obtient une équation du 4 degré.
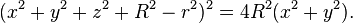

Pour R-r positif ou nul, on a :
Aire du tore :
Volume intérieur du tore :
Les théorèmes de Guldin permettent d'obtenir ces résultats, et aussi de déterminer les formules de l'aire et du volume du tore croisé (pour R Pour R>0, parmi les isométries remarquables du tore, on distingue : Les rotations ru d'axe (supposé orienté) D et d'angle u ; Le retournement a par rapport au plan affine P orthogonal à D passant par le centre de C ; Le retournement bQ par rapport à tout plan affine Q contenant D ; La symétrie centrale s par rapport au projeté orthogonal O de C sur D ; Les symétries axiales par rapport à toute droite passant par O et contenue dans P ; Les composées d'une rotation ru par le retournement a. Évidemment, la symétrie centrale et les symétries axiales s'obtiennent comme composées des retournements décrits. Le groupe G des isométries du tore est isomorphe au produit direct de Z/2Z par le produit semi-direct de S par Z/2Z : Un isomorphe naturel est décrit comme suit : ru correspond à (0,u,0) ; a correspond à (1,0,0) ; Pour un plan Q fixé arbitraire, bQ correspond à (0,0,1). En particulier, bru(Q)=rubQr-u correspond à (0,u,1) ; s correspond à (1,π,0) ; …... Le théorème des quatre couleurs ne s'applique pas pour un tore : il est possible de diviser la surface d'un tore en 7 zones de couleurs différentes (maximum) de sorte que chacune touche les 6 autres. La caractéristique d'Euler d'un tore est égale à 0 : il est possible de mailler le tore sans introduire de singularité. En recherche nucléaire pour la production d'énergie par fusion, dans les réacteurs de type tokamak, le plasma est contenu par de forts champs magnétiques dans une chambre de forme torique. L'un de ces réacteurs porte d'ailleurs le nom de Tore Supra. C'est aussi la forme des chambres à vide des accélérateurs de particules du type synchrotron (en négligeant les canaux d'entrée et de sortie). En électricité, la forme idéale du circuit magnétique d'un transformateur est celle du tore. En topologie, le terme tore est réservé pour désigner des espaces topologiques (ou des variétés). Il existe plusieurs présentations, toutes équivalentes à homéomorphisme (ou difféomorphisme) près. On appelle tore de dimension n ou n-tore, et l'on note T, l'espace topologique défini comme : produit de n copies du cercle unité S ; quotient de R par Z ; plus généralement, quotient d'un espace vectoriel réel E de dimension finie n par un réseau G ; Le tore de dimension n est une variété topologique compacte et connexe de dimension n. Obtenu comme quotient E/G, T est une variété différentielle et même un groupe de Lie abélien ; l'atlas maximal correspondant ne dépend ni du réseau, ni de l'espace vectoriel. Si E est un espace vectoriel euclidien, le quotient T = E/G se présente naturellement comme une variété plate. Pour construire un cercle, on peut joindre les extrémités d'un segment en le courbant dans un plan. De même, pour construire un 2-tore, on peut joindre deux à deux les côtés opposés d'un carré en le courbant dans une troisième dimension et plus généralement, pour construire un n-tore, on peut joindre deux à deux les faces (n – 1)-dimensionnelles opposées d'un hypercube de dimension n en courbant cet hypercube dans une nouvelle dimension n + 1. Ainsi, un 3-tore est le recollement des 3 paires de faces opposées d'un cube, dans une quatrième dimension. Le groupe fondamental de T est le groupe abélien libre à n générateurs, soit Z. Les tores sont les seuls groupes de Lie abéliens compacts connexes. L'introduction des tores maximaux (sous-groupes compacts abéliens connexes maximaux) est d'une importance capitale dans l'étude des groupes de Lie compacts. Des réservoirs toroïdes ou toriques (en forme de tore) sont présents dans plusieurs modèles de centrales nucléaires dont le récent AP 1000, ou les réacteurs de la série Mark. En cas de séisme important avec déplacement latéral du sol, d'explosion ou choc ayant les mêmes conséquences, le flushing (les ondes et vagues induites et leur effet de Ballottement) peut être une source de contraintes inhabituelles et différentiées dans le tore. Comprendre le flushing est donc un enjeu pour certaines technologies utilisant des réservoirs toriques, de même que pour les réservoirs circulaire ou toroïde dans un véhicule en déplacement, y compris avion, fusée ou véhicule spatial . La physique des plasmas formés dans les tores fait également l'objet de nombreuses études, dans le cadre du développement des Tokamaks et de la fusion nucléaire.Groupe des isométries
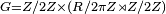 .
.
Cercles de Villarceau
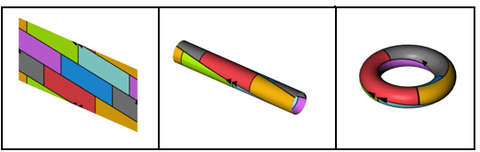
Colorier un tore
Caractéristique d'Euler d'un tore
Applications
Le tore de dimension n
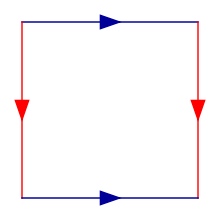
Dynamique d'un plasma ou d'un fluide dans un tore

在几何上,一个环面是一个冬甩形状的旋转曲面,由一个圆绕一个和该圆共面的一个轴回转所生成。球面可以视为环面的特殊情况,也就是旋转轴是该圆的直径时。若转轴和圆不相交,圆面中间有一个洞,就像一个甜甜圈,一个呼啦圈,或者一个充了气的轮胎。另一个情况,也就是轴是圆的一根弦的时候,就产生一个挤扁了的球面,就像一个圆的座垫那样。英文Torus曾是拉丁文的这种形状的座垫。 圆环面可以参数式地定义为: 其中 u, v ∈ [0, 2π], R是管子的中心到画面的中心的距离, r是圆管的半径。 直角坐标系中的关于z-轴方位角对称的环面方程是 该圆环面的表面积和内部体积如下 根据更一般的定义,环面的生成元不必是圆,而可以是椭圆或任何圆锥曲线。
一个环面是两个圆的乘积。 将一个有小洞的环面翻转。 拓扑学上,一个环面是一个定义为两个圆的积的闭合曲面:S × S。 上述曲面,若采用R诱导的相对拓扑,则同胚于一个拓扑环面,只要它不和自己的轴相交。 该环面也可用欧几里得平面的一个商空间来表述,这是通过如下的等价关系来完成的 (x,y) ~ (x+1,y) ~ (x,y+1) 或者等价地说,作为单位正方形将对边粘合的商空间,表述为基本多边形 。 环面的基本群是圆的基本群和自身的直积: 直观地讲,这意味着一个先绕着环面的“洞”(譬如,沿着某个纬度方向的圆)然后绕着环面“实体”(譬如,沿着特定经度方向的圆)的闭路径可以变形成为先绕实体后绕空心的路径。所以,严格的经度方向和严格的纬度方向的路径是可交换的。这可以想象成为两个鞋带互相穿过然后解开再系上。 环面的第一同调群和基本群同构(因为基本群是交换群)。
环面很容易推广到任意维。n维环面可以定义为n个圆的乘积: 上面所述的环面就是2维环面。1维环面就是圆。3维环面很难描述。和2维环面一样,n维环面可以表述为R在各个坐标方向整数平移下的商空间。也即,n维环面是R模(modulo)整数格点Z的群作用(该作用就是矢量和)。等价地说,n维环面是n维立方体把相对的面两两粘合起来得到的空间。 n维环是n维紧致流形的一个例子。它也是紧致可交换李群的一个例子。这是因为单位圆是一个紧致可交换李群(如果把它作为定义了乘法的单位长度复数来看)。环面上的群乘法可以定义为各坐标分别相乘。 环面群在紧致李群理论中有重要的作用。部分原因在于所有紧致李群中总是存在一个极大环面;也就是最大可能维度的闭子群环面。 n维环面的基本群是一个n阶自由可交换群。n维环面的k阶同调群是n取k阶的自由可交换群。因此可以推出n维环面的欧拉示性数 是0。上同调环H(T,Z)可以等同为Z-模 Z上的外代数,其生成元为n非平凡闭链的对偶。
如果把环面分成若干区域,那幺总是可以用最多7种颜色来着色,使得每对相邻区域有不同的颜色。(这和四色问题不同。)在下面的例子中,环面被分为7个区域,两两相邻,说明7色是必须的:
tore nom commun - masculin ( tores )