Les infinitésimaux (ou infiniment petits) ont été utilisés pour exprimer l'idée d'objets si petits qu'il n'y a pas moyen de les voir ou de les mesurer. Le mot « infinitésimal » vient de infinitesimus (latin du XVII siècle), ce qui signifiait à l'origine l'élément « infini-ème » dans une série. Selon la notation de Leibniz, si x est une quantité, dx et Δx peuvent représenter une quantité infinitésimale de x.
Historique
Dans le langage courant, un objet infiniment petit est un objet qui est plus petit que toute mesure possible, donc non pas d'une taille zéro, mais si petit qu'il ne peut être distingué de zéro par aucun moyen disponible. Par conséquent, lorsqu'il est utilisé en tant qu'adjectif, «infinitésimal» dans le langage vernaculaire signifie « extrêmement faible ».
Archimède exploita les infinitésimaux dans La Méthode pour trouver des aires des régions et des volumes de solides. Les auteurs classiques avaient tendance à chercher à remplacer les arguments infinitésimaux par des arguments utilisant la méthode d'exhaustion, qu'ils jugeaient plus fiable. Le XV siècle a vu le travail pionnier de Nicolas de Cues, développé au XVII siècle par Johannes Kepler, en particulier le calcul de l'aire d'un cercle en représentant celui-ci comme un polygone d'un nombre infini de côtés. Simon Stevin élabora un continu de décimaux au XVI siècle. La méthode des indivisibles de Bonaventura Cavalieri conduit à une extension des résultats des auteurs classiques. La méthode des indivisibles traitait des figures géométriques comme étant composés d'entités de codimension 1. Les infinitésimaux de John Wallis diffèrent des indivisibles en ce sens que des figures géométriques se décomposeraient en des parties infiniment minces de la même dimension que la figure, préparant le terrain pour des méthodes générales du calcul intégral. Il exploita un infinitésimal notée 1 ∞ / 0 {\displaystyle {\frac {1}{\infty /0}}} dans les calculs de superficie.
Pierre de Fermat, inspiré par Diophante, développa le concept d'adégalité, c'est-à-dire égalité « adéquate » ou égalité approximative (avec une erreur infime), qui a fini par jouer un rôle clé dans une mise en œuvre mathématique moderne des définitions infinitésimales de la dérivée et l'intégrale. L'utilisation des infinitésimaux chez Leibniz s'appuya sur un principe heuristique appelé la loi de continuité : ce qui réussit pour les nombres finis réussit aussi pour les nombres infinis, et vice versa. Le XVIII siècle a vu l'utilisation systématique des infiniment petits par les plus grands tels que Leonhard Euler et Joseph Lagrange. Augustin-Louis Cauchy exploita les infinitésimaux dans sa définition de la continuité et dans une forme préliminaire d'une fonction delta de Dirac. Lorsque Georg Cantor et Dedekind développaient des versions plus abstraites du continu de Stevin, Paul du Bois-Reymond a écrit une série d'articles sur des continus enrichis d'infinitésimaux sur la base des taux de croissance des fonctions. L'œuvre de du Bois-Reymond a inspiré à la fois Émile Borel et Thoralf Skolem. Skolem développa les premiers modèles non standard de l'arithmétique en 1934. Une mise en œuvre mathématique à la fois de la loi de continuité et des infinitésimaux a été réalisée par Abraham Robinson en 1961, qui a développé l'analyse non standard basée sur des travaux antérieurs de Edwin Hewitt en 1948 et Jerzy Łoś (de) en 1955. Les hyperréels constituent un continu enrichi d'infinitésimaux, tandis que le principe du transfert (en) met en œuvre la loi de continuité de Leibniz.
En analyse mathématique
En mathématiques, le terme infiniment petit peut s'appliquer :
à une quantité négligeable dans le cadre de méthodes d'étude du comportement d'une fonction au voisinage d'un point (ou de l'infini), en regard du comportement d'une autre fonction, souvent choisie sur une échelle de référence.
à une notion historique de nombre infinitésimal, abandonnée par les élèves de Karl Weierstrass, qui donna un fondement rigoureux à la notion de limite. Cette notion avait déjà été entrevue mais jamais explicitée, en particulier parce que les représentations et la définition des nombres réels avaient demandé une longue maturation.
à un nombre hyperréel plus petit en valeur absolue que tout inverse d’un entier, dans le cadre de l'analyse non standard de Robinson qui formalisa les infinitésimaux de Leibniz ;
de façon plus classique, en analyse réelle, dans l'expression « infiniment petits équivalents » : deux fonctions f {\displaystyle f} et g {\displaystyle g} sont des infiniment petits équivalents au voisinage de a si, f ( x ) {\displaystyle f(x)} et g ( x ) {\displaystyle g(x)} tendant tous deux vers zéro quand x tend vers a, le rapport f ( x ) / g ( x ) {\displaystyle f(x)/g(x)} tend vers 1 : lim x → a f ( x ) g ( x ) = 1. {\displaystyle \lim _{x\to a}{\frac {f(x)}{g(x)}}=1.}
Ainsi, la longueur d'un arc de cercle et celle de sa corde, en tant que fonctions de l'angle au centre associé, sont des infiniment petits équivalents au voisinage de l'angle nul.
Infiniment grands
De même, deux fonctions
et
sont des infiniment grands équivalents au voisinage de a si,
et
tendant tous deux vers l'infini quand x tend vers a, le rapport
tend vers 1. En analyse non standard, les infiniment grands sont des hyperréels qui sont les inverses des infiniment petits.
Médias
Les expressions « infiniment petit » et « infiniment grand » sont très notoires et presque jamais utilisées dans leur sens premier, mais pour parler de sujets tels que les galaxies, les quarks, et les nanotechnologies.
Littérature
Dans le fragment 199 des Pensées, Blaise Pascal écrit que « l’homme est infiniment éloigné de comprendre les extrêmes », coincé entre l'infiniment petit et l'infiniment grand, « incapable de voir […] l’infini où il est englouti ». Il imagine des mondes homothétiquement réduits, de plus en plus petits : « Qu'un ciron lui offre dans la petitesse de son corps des parties incomparablement plus petites, des jambes avec des jointures, des veines dans ces jambes, du sang dans ces veines, des humeurs dans ce sang, des gouttes dans ces humeurs, des vapeurs dans ces gouttes ; que, divisant encore ces dernières choses, il épuise ses forces en ces conceptions, et que le dernier objet où il peut arriver soit maintenant celui de notre discours ; il pensera peut-être que c'est là l'extrême petitesse de la nature. Je veux lui faire voir là dedans un abîme nouveau. Je lui veux peindre non seulement l'univers visible, mais l'immensité qu'on peut concevoir de la nature, dans l'enceinte de ce raccourci d'atome. Qu'il y voie une infinité d'univers, dont chacun a son firmament, ses planètes, sa terre, en la même proportion que le monde visible; dans cette terre, des animaux, et enfin des cirons, dans lesquels il retrouvera ce que les premiers ont donné… »
Dans le même ouvrage, Pascal invoque la « sphère dont le centre est partout, la circonférence nulle part » , ce qui est une image traditionnelle dans la pensée occidentale, on la retrouve chez Nicolas de Cues, Giordano Bruno, Maître Eckhart, Boèce, elle a été attribuée à Empédocle.

 词典释义:
词典释义:
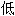 的,最少的;
的,最少的;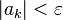
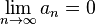
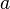 被称为
被称为 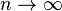 时的无穷小量。
时的无穷小量。