Le spin est, en physique quantique, une des propriétés des particules, au même titre que la masse ou la charge électrique. Comme d'autres observables quantiques, sa mesure donne des valeurs discrètes et est soumise au principe d'incertitude. C'est la seule observable quantique qui ne présente pas d'équivalent classique, contrairement, par exemple, à la position, l'impulsion ou l'énergie d'une particule.
Le spin a d'importantes implications théoriques et pratiques. Il influence pratiquement tout le monde physique. Il est responsable du moment magnétique de spin et donc de l'effet Zeeman anomal (parfois incorrectement appelé « anormal ») qui en découle. Les particules sont classées selon la valeur de leur nombre quantique de spin (aussi appelé communément, le spin) : les bosons de spin entier ou nul et les fermions de spin demi-entier. Fermions et bosons se comportent différemment dans des systèmes comprenant plusieurs particules identiques ; le comportement fermionique de l'électron est ainsi la cause du principe d'exclusion de Pauli et des irrégularités de la table périodique des éléments. L'interaction spin-orbite conduit à la structure fine du spectre atomique. Le spin de l'électron joue un rôle important dans le magnétisme, et la manipulation des courants de spins dans des nano-circuits conduit à un nouveau champ de recherche : la spintronique. La manipulation des spins nucléaires par résonance magnétique nucléaire est importante dans la spectroscopie RMN et l'imagerie médicale (IRM). Le spin du photon – ou plus exactement son hélicité – est associé à la polarisation de la lumière.
Historique
La genèse du concept de spin fut l'une des plus difficiles de l'histoire de la physique quantique au début du XX siècle. L'effet Zeeman anomal, la structure hyperfine des raies spectrales ou encore l'expérience de Stern et Gerlach (1922) posaient à cette époque de grosses difficultés d'interprétation. La découverte du spin par Samuel Goudsmit et George Uhlenbeck en septembre 1925 a été révolutionnaire. Immédiatement après la publication de ce concept, un problème de facteur 2 dans la structure fine du spectre de l'hydrogène, identifié par Heisenberg, fut résolu par les deux physiciens et publié en décembre 1925. Leur interprétation incorporait la nouvelle notion de spin.
Le spin a d'abord été interprété comme un degré de liberté supplémentaire, s'ajoutant aux trois degrés de liberté de translation de l'électron : son moment cinétique intrinsèque (ou propre). En d'autres termes, l'électron ponctuel était vu comme tournant sur lui-même — d'où le nom de « spin », en anglais « tourner rapidement ». Cependant, il est vite apparu que cette « rotation » est purement quantique, et n'a pas d'équivalent en mécanique classique. La représentation du spin en termes de simple rotation est donc abandonnée. Wolfgang Pauli avait déjà montré en 1924 que, compte tenu des dimensions connues de l'électron, une rotation de l'électron nécessiterait une vitesse tangentielle de rotation à son équateur qui serait supérieure à la vitesse de la lumière, vitesse en principe infranchissable selon la théorie de la relativité restreinte.
La notion théorique de spin a été introduite par Pauli en décembre 1924 pour l'électron, afin d'expliquer un résultat expérimental qui restait incompréhensible dans le cadre naissant de la mécanique quantique non-relativiste : l'effet Zeeman anomal. L'approche développée par Pauli consistait à introduire de façon ad hoc le spin en ajoutant un postulat supplémentaire aux autres postulats de la mécanique quantique non-relativiste (équation de Schrödinger, etc.).
En 1927, Wolfgang Pauli a proposé la modélisation du spin en termes de matrices, ce qui correspond à une écriture en termes d'opérateurs sur la fonction d'onde intervenants dans l'équation de Schrödinger : l'équation de Pauli. En 1928, à partir de l'équation de Klein-Gordon, Paul Dirac démontra qu'une particule ayant un spin non nul vérifie une équation relativiste, appelée aujourd'hui équation de Dirac.
Enfin, c'est en théorie quantique des champs que le spin montre son caractère le plus fondamental. L'analyse du groupe de Poincaré effectuée par Wigner en 1939 montra en effet qu'une particule est associée à un champ quantique, opérateur qui se transforme comme une représentation irréductible du groupe de Poincaré. Ces représentations irréductibles se classent par deux nombres réels positifs : la masse et le spin.
Le spin du photon a été mis en évidence expérimentalement par Râman et Bhagavantam en 1931.
Le moment cinétique de spin
Le spin est le moment cinétique intrinsèque des particules quantiques. Il est donc soumis aux mêmes lois générales qui régissent tout autre moment cinétique quantique, tel que, par exemple, le moment cinétique orbital.
Le spin est donc un opérateur vectoriel hermitien comportant trois composantes, notées usuellement et par référence aux trois axes de coordonnées cartésiennes de l'espace physique. Ces composantes sont des observables vérifiant les relations de commutations caractéristiques d'un moment cinétique:
-
![\left[ \, \hat{S}_i \, , \ \hat{S}_j \, \right] \ = \ i \ \hbar \ \epsilon_{ijk} \ \hat{S}_k](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/5166781c**e62f3f9145f53e8a8d4d88.png)
où est le symbole de Levi-Civita et
-
![\left [\hat S^2, \hat S_i \right ]=0](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/6f88f511ea9510cbb28f230aaa7efb50.png) .
.
Ces relations de commutations sont analogues à celles découvertes en novembre 1925 par Born, Heisenberg et Jordan pour les composantes du moment cinétique orbital. Ces relations de commutations impliquent que le principe d'incertitude s'applique aux mesures du spin faites dans les différentes directions de l'espace : on peut en effet mesurer très exactement la norme du vecteur et une projection sur un axe de coordonnées, mais les deux autres projections sur les deux autres axes orthogonaux ne sont plus alors mesurables précisément.
Par analogie avec les résultats obtenus pour le moment cinétique orbital (ou plus généralement pour un moment cinétique quantique), il e**ste pour l'opérateur spin une base de vecteurs propres notés , où est entier ou demi-entier, et est un entier ou demi-entier prenant l'une des valeurs , tels que :
-

-

Le nombre est un nombre quantique qui est aussi appelé le spin (de manière impropre toutefois).
Les valeurs propres des opérateurs  et
et  représentent l'ensemble des mesures possibles pour les deux observables, c'est-à-dire respectivement le carré de la norme, et la projection sur un axe
représentent l'ensemble des mesures possibles pour les deux observables, c'est-à-dire respectivement le carré de la norme, et la projection sur un axe 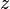 arbitraire dans l'espace.
arbitraire dans l'espace.
Spin des particules élémentaires et composites
La totalité des particules connues ou d'e**stence fortement suspectée a un nombre quantique de spin compris entre 0 et 2. En particulier pour les particules élémentaires.
Spin 0 : le boson de Higgs ;
Spin 1/2 : l'électron, le positron, les neutrinos, les quarks, etc.;
Spin 1 : le photon, le gluon vecteur de l'interaction forte, les bosons W et Z vecteurs de l'interaction faible ;
Spin 2 : le graviton, particule hypothétique vecteur de la gravitation.
Il n'e**ste pas de particule élémentaire connue de spin 3/2, mais la supersymétrie, si elle e**ste, en prédit une, le gravitino.
Le spin (à l'état fondamental) des particules composées de plusieurs particules élémentaires, comme le proton, le neutron, tout noyau atomique ou atome, est constitué des spins des particules qui les composent auquel s'ajoute le moment cinétique orbital des différentes particules élémentaires :
Spin 0 : noyaux atomiques tels que C, O, Si… et de manière générale les noyaux composés d'un nombre pair de protons et de neutrons ;
Spin 1/2 : le proton, le neutron, certains noyaux atomiques : ex. C, Si, etc. ;
Spin > 1/2 : 75 % des isotopes stables (voir par exemple l'article résonance magnétique nucléaire).
Il n'est pas toujours facile de déduire le spin d'une particule à partir de principes simples ; par exemple, même s'il est connu que le proton a un spin 1/2, la question de savoir comment les particules élémentaires qui le composent sont arrangées est toujours un sujet actif de recherche (voir Spin des nucléons (en)).
Pour une raison assez complexe démontrée dans le cadre de ce qui est appelé théorème spin-statistique, la valeur entière ou demi-entière du spin détermine une propriété cruciale de la particule : si son spin est entier, c'est un boson, si son spin est demi-entier, c'est un fermion.
Spin 1/2 - matrices de Pauli
Pour une particule de nombre quantique de spin  comme l'électron, le proton ou le neutron, donc
comme l'électron, le proton ou le neutron, donc  : il e**ste seulement deux états de spin distincts, caractérisés par
: il e**ste seulement deux états de spin distincts, caractérisés par  .
.
On note souvent les deux états propres correspondants : 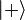 et
et 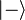 , ou encore :
, ou encore :  et
et  .
.
Pauli a introduit trois matrices 2 × 2, notées telles que l'opérateur de spin s'écrive :
-

Ces trois matrices de Pauli s'écrivent explicitement :
-

Elles satisfont les relations de commutation :
-
![\left[ \, \hat{\sigma}_i \, , \ \hat{\sigma}_j \, \right] \ = \ 2 \ i \ \epsilon_{ijk} \ \hat{\sigma}_k](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/ae7355a174a94fa7dbf4cf267bd49a61.png)
Il a été remarqué qu'il s'agit là des relations entre quaternions découvertes par William Rowan Hamilton, ce qui donne une représentation plus compacte des opérateurs de spin.
Orientation du spin
Composantes du spin et multiplicité de spin
En mécanique classique, le moment angulaire d'une particule possède non seulement une magnitude (vitesse de rotation de la particule), mais également une direction (direction de l'axe de rotation de la particule).
En mécanique quantique, le moment angulaire de spin (spin) contient également ces informations, mais dans une forme plus subtile. La mécanique quantique montre en effet, par l'intermédiaire des équations (1) et (2) ci-dessus (voir #Le moment cinétique de spin), que si l'état du moment angulaire de spin est l'un des états propres de , la composante du spin mesurée selon une direction quelconque, c'est-à-dire sa projection sur un axe quelconque (par exemple l'axe z), ne peut prendre que les valeurs quantifiées suivantes :
-

où s est le nombre quantique de spin de la particule. On peut constater qu'il e**ste 2s+1 valeurs possibles de . Le nombre 2s+1 est appelé la multiplicité de spin. Par exemple, il n'y a que deux valeurs possibles pour une particule de spin 1/2 : = +1/2 ou -1/2. Cela correspond à deux états quantiques, notés symboliquement et , pour lesquels la projection du spin pointe respectivement dans la direction +z ou -z. La valeur de la projection dans les autres directions de l'espace, x ou y par exemple, est par contre indéterminée, du fait des relations de non-commutation (ou d'« incertitude ») entre les trois composantes du spin. En d'autres termes, si on ne s'intéresse qu'à un spin individuel, il n'est pas possible de déterminer avec précision sa direction dans l'espace (c'est en quelque sorte l'équivalent du principe d'incertitude de Heisenberg en ce qui concerne la vitesse et la position d'une particule, qui ne peuvent pas être déterminées simultanément).
Représentation géométrique du spin par une sphère de Riemann

Représentation géométrique d'un état de spin 1/2 par une sphère de Riemann
Un état quantique quelconque d'une particule isolée de spin s=1/2 peut s'exprimer sous la forme générale :
-

où a et b sont deux nombres complexes. Cette formule exprime une superposition des deux états propres.
Penrose montre que l'état de spin 1/2 peut être caractérisé par le rapport des deux nombres complexes . Si cette valeur est projetée sur une sphère de Riemann, qui permet de représenter l'ensemble des nombres complexes, il est possible d'établir une correspondance entre un état de spin et une direction dans l'espace ordinaire.
Selon cette représentation, tout état quantique d'un spin s=1/2 correspond à un point sur la sphère dont la projection stéréographique sur le plan complexe (le plan équatorial de la sphère) est ce rapport u. Ce point définit un vecteur correspondant à l'orientation de la polarisation d'un ensemble de spins placés dans le même état (voir #Signification physique du vecteur d'orientation du spin).
Représentation sur une sphère de Bloch

Représentation de la direction moyenne (ou « polarisation ») du moment angulaire d'un spin s=1/2 par rapport à un axe z choisi arbitrairement comme axe de quantification
Une autre représentation est possible, celle de la sphère de Bloch.
Dans cette représentation, les coefficients a et b sont définis en utilisant des coordonnées angulaires sphériques :


Le vecteur représentant l'état  est alors représenté comme sur la figure ci-contre. Cette représentation est bien entendu parfaitement équivalente à la représentation précédente sur une sphère de Riemann, pour laquelle le rapport u vaut :
est alors représenté comme sur la figure ci-contre. Cette représentation est bien entendu parfaitement équivalente à la représentation précédente sur une sphère de Riemann, pour laquelle le rapport u vaut :

Signification physique du vecteur d'orientation du spin
Les représentations précédentes ne représentent pas la direction proprement dite du spin (laquelle est indéterminée comme il a été dit plus haut) mais la direction moyenne d'un spin préparé dans un état particulier sur lequel un grand nombre de mesures seraient réalisées, ou bien encore d'un ensemble statistiquement significatif de particules placées dans le même état sur lequel un nombre réduit de mesures (voire une seule) seraient faites. Ces deux types de mesures donnent le même résultat, d'après le principe ergodique de Gibbs.
Pour un système préparé dans un état quantique de spin quelconque, il n'est possible en effet de décrire les trois projections d'un moment angulaire spin sur trois axes orthogonaux que par des valeurs moyennes:

Le vecteur défini par les trois projections décrit une « direction » vers laquelle la direction moyenne du moment angulaire du spin pointe, et qu'il est judicieux d'appeler polarisation. C'est exactement l'orientation de ce vecteur qui a été représentée précédemment sur la sphère de Riemann ou de Bloch. Il s'avère que ce vecteur de polarisation du spin a une signification physique pratique notamment en spectroscopie de résonance magnétique nucléaire (RMN). Dans cette technique, les spins des protons (ou de tout autre noyau atomique possédant un spin non nul) peuvent être préparés dans n'importe quel état donné. Par exemple, si le système de spin est placé dans un champ magnétique homogène, la polarisation moyenne à l'équilibre thermodynamique correspond à l'état . L'application d'impulsions radiofréquence choisies permet ensuite de polariser les spins dans n'importe quelle autre direction de l'espace. Le signal RMN ma**mum est obtenu lorsque la bobine de détection est placée dans la direction de cette polarisation. Dans le cas de l'électron, la spectroscopie de résonance paramagnétique électronique (RPE) est fondée sur exactement les mêmes principes.
L'expérience de Stern et Gerlach

Différence entre le spin 1/2 de l'électron et un aimant classique, à travers l'expérience de Stern et Gerlach
Moment magnétique de spin
Définition. Facteur de Landé
Au moment cinétique orbital d'une particule de charge et de masse est associé un moment magnétique orbital :
-

Le facteur est appelé rapport gyromagnétique. De même, on associe à une particule de charge , de masse , et de spin donné un moment magnétique de spin :
-

où est un nombre sans dimension, appelé facteur de Landé (1921). Ce nombre varie selon la nature de la particule : on a appro**mativement pour l'électron, pour le proton, et pour le neutron. On trouve aussi des valeurs moitié pour le proton et le neutron qui correspondraient à un moment magnétique anomal.
Magnéton de Bohr
Pour l'électron, on a les valeurs suivantes : et ; on introduit alors le « quantum magnétique » suivant, appelé magnéton de Bohr :
Moment magnétique anomal de l'électron
L'équation de Dirac prédit pour l'électron un facteur de Landé exactement égal à :  . Or, la valeur expérimentale admise en 2005 vaut :
. Or, la valeur expérimentale admise en 2005 vaut :
-

Il e**ste donc un écart, décelé pour la première fois en 1947 dans la structure hyperfine de l'hydrogène et du deutérium : on parle alors du moment magnétique anomal de l'électron. La théorie quantique des champs du modèle standard permet de rendre compte de cette anomalie avec une très grande précision.
Spin et représentation de groupes
L'analyse du comportement des objets sous l'effet des rotations nécessite de prendre en compte la structure mathématique de groupe formé par celles-ci. À un objet se transformant sous les rotations est alors associée une représentation de groupe. Deux objets ayant des propriétés de symétrie similaires seront donc associés à des représentations équivalentes du groupe des rotations. De ce point de vue, le spin n'est rien d'autre qu'un nombre qui permet de classifier les différentes représentations irréductibles non équivalentes du groupe des rotations.
Le spin dans l'art
![Father et Mother de la série Spin Family (2009), par le physicien et sculpteur Julian Voss-Andreae. Les deux objets représentés illustrent la géométrie d’un objet de spin 5/2 (le « mâle » bleu à gauche) et d’un objet de spin 2 (la « femelle » rose à droite). L’œuvre Spin Family, présentée dans l’exposition « Quantum Objects », compare avec humour les fermions au sexe masculin et les bosons au sexe féminin. Les objets de spin 1/2, 1, 3/2, 2 et 5/2 constituent alors une famille de 5 personnes[19].](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/%22Father%22_and_%22Mother%22_of_the_series_%22Spin_Family%22.jpg)
Father et Mother de la série Spin Family (2009), par le physicien et sculpteur Julian Voss-Andreae. Les deux objets représentés illustrent la géométrie d’un objet de spin 5/2 (le « mâle » bleu à gauche) et d’un objet de spin 2 (la « femelle » rose à droite). L’œuvre Spin Family, présentée dans l’exposition « Quantum Objects », compare avec humour les fermions au sexe masculin et les bosons au sexe féminin. Les objets de spin 1/2, 1, 3/2, 2 et 5/2 constituent alors une famille de 5 personnes.

 词典释义:
词典释义:
![\left[ \, \hat{S}_i \, , \ \hat{S}_j \, \right] \ = \ i \ \hbar \ \epsilon_{ijk} \ \hat{S}_k](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/5166781c**e62f3f9145f53e8a8d4d88.png)
![\left [\hat S^2, \hat S_i \right ]=0](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/6f88f511ea9510cbb28f230aaa7efb50.png) .
.


 et
et  représentent l'ensemble des mesures possibles pour les deux observables, c'est-à-dire respectivement le carré de la norme, et la projection sur un axe
représentent l'ensemble des mesures possibles pour les deux observables, c'est-à-dire respectivement le carré de la norme, et la projection sur un axe 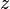 arbitraire dans l'espace.
arbitraire dans l'espace. comme l'électron, le proton ou le neutron, donc
comme l'électron, le proton ou le neutron, donc 
 .
.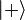 et
et 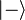 , ou encore
, ou encore et
et  .
.

![\left[ \, \hat{\sigma}_i \, , \ \hat{\sigma}_j \, \right] \ = \ 2 \ i \ \epsilon_{ijk} \ \hat{\sigma}_k](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/ae7355a174a94fa7dbf4cf267bd49a61.png)






 est alors représenté comme sur la figure ci-contre. Cette représentation est bien entendu parfaitement équivalente à la représentation précédente sur une sphère de Riemann, pour laquelle le rapport u vaut
est alors représenté comme sur la figure ci-contre. Cette représentation est bien entendu parfaitement équivalente à la représentation précédente sur une sphère de Riemann, pour laquelle le rapport u vaut




 . Or, la valeur expérimentale admise en 2005 vaut
. Or, la valeur expérimentale admise en 2005 vaut
![Father et Mother de la série Spin Family (2009), par le physicien et sculpteur Julian Voss-Andreae. Les deux objets représentés illustrent la géométrie d’un objet de spin 5/2 (le « mâle » bleu à gauche) et d’un objet de spin 2 (la « femelle » rose à droite). L’œuvre Spin Family, présentée dans l’exposition « Quantum Objects », compare avec humour les fermions au sexe masculin et les bosons au sexe féminin. Les objets de spin 1/2, 1, 3/2, 2 et 5/2 constituent alors une famille de 5 personnes[19].](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/%22Father%22_and_%22Mother%22_of_the_series_%22Spin_Family%22.jpg)