Système de coordonnées cartésiennes dans un plan
Système de coordonnées cartésiennes en 3 dimensions
En mathématiques, un système de coordonnées permet de faire correspondre à chaque point d'un espace à N dimensions, un (et un seul) N-uplet de scalaires. Dans beaucoup de cas, les scalaires considérés sont des nombres réels, mais il est possible d'utiliser des nombres complexes ou des éléments d'un corps commutatif quelconque. Plus généralement, les coordonnées peuvent provenir d'un anneau ou d'une autre structure algébrique apparentée.
On considère que l'espace existe en lui-même indépendamment du choix d'un système de coordonnées particulier.
Exemples
Le cas le plus courant est la notion de coordonnées en géométrie, voir l'article Repérage dans le plan et dans l'espace : on choisit un point de repère appelé « origine », et trois « axes » (les « règles graduées ») de directions distinctes qui ne sont pas dans le même plan (dans le plan, deux directions suffisent). Les coordonnées de ce point sont appelées « abscisse », « ordonnée » et « cote », et sont notées respectivement x, y et z. Voir aussi l'article Géométrie analytique.
En géographie, on associe une longitude et une latitude à des endroits géographiques ; c'est un système de coordonnées. Dans ce cas, la paramétrisation n'est pas unique aux pôles Nord et Sud.
Un exemple de système de coordonnées permet de décrire un point P dans l'espace euclidien par un n-uplet :
-

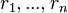 étant des nombres réels appelés coordonnées du point P.
étant des nombres réels appelés coordonnées du point P.
Si un sous-ensemble S d'un espace euclidien est appliqué de façon continue sur un autre espace topologique, cela définit les coordonnées de l'image de S. On peut parler de paramétrisation de l'image, puisque ce processus assigne des nombres aux points. La correspondance est unique seulement si l'application est bijective.
Transformations
Une transformation de coordonnées est une conversion d'un système à un autre pour décrire le même espace.
Certains choix de système de coordonnées peuvent conduire à des paradoxes, par exemple au voisinage d'un trou noir, qui peuvent être résolus en changeant de système. Cela n'est toutefois pas possible en une véritable singularité mathématique.
Systèmes courants
Quelques systèmes de coordonnées couramment utilisés :
le système de coordonnées cartésiennes utilisé dans un espace vectoriel ou un espace affine de dimension finie.
pour tout espace vectoriel de dimension finie et toute base, les coefficients des vecteurs exprimés dans cette base peuvent être utilisés comme coordonnées. Changer de base est une transformation de coordonnées, une transformation linéaire qui peut être définie par une matrice.
le système de coordonnées curvilignes est une généralisation, basée sur des intersections de courbes.
les systèmes de coordonnées polaires : le système de coordonnées cylindriques représente un point dans l'espace par un angle, une distance à l'origine et une hauteur. le système de coordonnées sphériques représente un point dans l'espace par deux angles et une distance à l'origine. Le système de coordonnées géographiques en est dérivé.
le système de coordonnées cylindriques représente un point dans l'espace par un angle, une distance à l'origine et une hauteur.
le système de coordonnées sphériques représente un point dans l'espace par deux angles et une distance à l'origine. Le système de coordonnées géographiques en est dérivé.
des systèmes de coordonnées généralisées sont utilisés en mécanique lagrangienne.
Systèmes utilisés en astronomie
L'astronomie utilise plusieurs systèmes de coordonnées pour noter la direction d'un objet céleste :
systèmes de coordonnées célestes : système de coordonnées horizontales, coordonnées locales liées à un point donné de la Terre ; système de coordonnées horaires, défini à partir du plan équatorial terrestre et de la direction du Nord géographique local ; système de coordonnées équatoriales, défini à partir du plan équatorial terrestre, et du point γ (direction correspondant au passage de la déclinaison du Soleil d'une valeur négative à une valeur positive) ; système de coordonnées écliptiques, défini à partir du plan de révolution de la Terre autour du Soleil ; ce système peut être géocentrique ou héliocentrique (ce dernier choix permet de déterminer des coordonnées non sujettes à la précession) ; système de coordonnées galactiques, défini à partir d'un plan fondamental, choisi une fois pour toutes, et situé au voisinage du plan de symétrie de notre Galaxie (contenu dans le disque, où se trouve le Soleil) ; ces coordonnées ne sont pas sujettes à la précession séculaire, dues au déplacement du système solaire (environ 250 km/s) au sein de notre Galaxie ;
système de coordonnées horizontales, coordonnées locales liées à un point donné de la Terre ;
système de coordonnées horaires, défini à partir du plan équatorial terrestre et de la direction du Nord géographique local ;
système de coordonnées équatoriales, défini à partir du plan équatorial terrestre, et du point γ (direction correspondant au passage de la déclinaison du Soleil d'une valeur négative à une valeur positive) ;
système de coordonnées écliptiques, défini à partir du plan de révolution de la Terre autour du Soleil ; ce système peut être géocentrique ou héliocentrique (ce dernier choix permet de déterminer des coordonnées non sujettes à la précession) ;
système de coordonnées galactiques, défini à partir d'un plan fondamental, choisi une fois pour toutes, et situé au voisinage du plan de symétrie de notre Galaxie (contenu dans le disque, où se trouve le Soleil) ; ces coordonnées ne sont pas sujettes à la précession séculaire, dues au déplacement du système solaire (environ 250 km/s) au sein de notre Galaxie ;
systèmes de coordonnées extragalactiques : système de coordonnées supergalactiques, basé sur le plan du superamas de galaxies local
système de coordonnées supergalactiques, basé sur le plan du superamas de galaxies local
Autres
En relativité générale, certains systèmes de coordonnées sont choisis de façon à simplifier les calculs.
Un système de coordonnées harmoniques représente un système de coordonnées qui, vues comme étant des champs vectoriels sont de laplacien nul.
Plus généralement, le système de coordonnées est essentiellement arbitraire en relativité générale, la structure des équations ne dépendant pas du choix de coordonnées. Cependant, lorsque vient la phase de résolution des équations du champ gravitationnel, certains systèmes de coordonnées s'avèrent plus commodes que d'autres, ou permettent une interprétation physique simple des résultats obtenus. Les classes de systèmes de coordonnées possédant telle ou telle propriété sont appelés jauge. Dans le domaine de la théorie des perturbations cosmologiques, le choix d'une telle jauge peut présenter des avantages.
Articles connexes
système de coordonnées (cartographie)

 词典释义:
词典释义:
 ,
, 整,一致性;
整,一致性; 定义的;
定义的;
 的,有条理的;
的,有条理的;


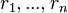 étant des nombres réels appelés coordonnées du point P.
étant des nombres réels appelés coordonnées du point P.