词典释义：
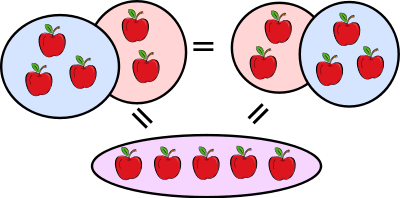
词：La multiplication de 3 par 2 donne le même résultat que la multiplication de 2 par 3.
En mathématiques, et plus précisément en algèbre générale, une loi de composition interne sur un ensemble S est dite commutative lorsque, pour tous x et y dans S,
.
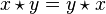Exemples
Les exemples les plus simples de lois commutatives sont sans doute l'addition et la multiplication des entiers naturels. L'addition et la multiplication des nombres réels et des nombres complexes, l'addition des vecteurs, l'intersection et la réunion des ensembles sont également des lois commutatives.
À l'inverse, la soustraction, la division, la multiplication des matrices, la composition de fonctions et la multiplication des quaternions sont des lois non commutatives.
Histoire
Certains écrits de l'Antiquité utilisent implicitement des propriétés de commutativité. Les Égyptiens utilisaient la commutativité de la multiplication pour simplifier les calculs de produits. Euclide, dans ses Éléments, avait aussi supposé la commutativité de la multiplication. La définition formelle de la commutativité a émergé à la fin du XVIII et au début du XIX siècle, lorsque les mathématiciens ont commencé à construire une théorie des fonctions. Aujourd'hui, la propriété de commutativité est considérée comme une propriété basique, utilisée dans la plupart des branches des mathématiques.
La première apparition du terme « commutatif » remonte à un article aux Annales de Gergonne écrit par François-Joseph Servois en 1814, où celui-ci étudiait les propriétés de fonctions qui commutent entre elles (par composition). L'expression commutative law (en anglais) est ensuite apparue dans les Philosophical Transactions en 1844, sous la plume de George Boole.
Structures à lois commutatives
Les structures suivantes ont pour point commun d'être décrites par la donnée d'une ou plusieurs lois internes dont on exige la commutativité :
les groupes commutatifs (on dit aussi « groupes abéliens ») ;
les anneaux commutatifs ;
les corps commutatifs.
Éléments permutables
Soit S un ensemble muni d'une loi de composition interne 
. Deux éléments x et y de S sont dits permutables lorsque :
.
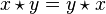On dit aussi que x et y commutent.
Ainsi, est commutative si et seulement si deux éléments quelconques de S sont toujours permutables.
交换律是被普遍使用的一个数学名词，意指能改变某物的顺序而不改变其最终结果。交换律是大多数数学分支中的基本性质，而且许多的数学证明需要倚靠交换律。简单运算的交换律许久都被假定存在，且没有给定其一特定的名称，直到19世纪，数学家开始形式化数学理论之后。
一般用法
交换律是一个和二元运算及函数有关的性质。而若交换律对一特定二元运算下的一对元素成立，则称这两个元素为在此运算下是「可交换」的。 在群论和集合论中，许多的代数结构被称做是可交换的，若其中的运算域满足交换律。在数学分析和线性代数中，一些知名的运算（如实数及复数上的加法和乘法）的交换律会经常被用于（或假定存在于）证明之中。
数学定义
一个不满足上述性质的运算则称之为「不可交换」的。
历史
对这一词第一个已知的应用是在1814年的一本法国期刊上 对交换律假定存在的应用早在很久之前便已有所记戴。埃及人用乘法的交换律来简化乘积的计算。且知欧几里得在《几何原本》中已有假定了乘法交换律的存在。对交换律形式上的应用产生于18世纪末19世纪初，那时数学家开始在研究函数的理论。今日，交换律已被普遍认知，且在大多数的数学分支中被当做基本性质来使用。交换律的简易版本通常会在初等数学教程中被教导。 第一个使用「可交换（commutative）」一词的是 Francois Servois 于1814年写下的笔记，这一词在笔记中被用来指有着现在称之为交换律的函数。这一词首次出现于英语中的是在1844年的英国皇家学会哲学汇刊中。