C'était hyper important pour moi d'avoir la symétrie pour structurer cet espace.
对我来说,这个空间结构的对称性非常重要。
[Une Fille, Un Style]
S’étendant sur 273 hectares, vous y observerez des bâtiments anciens et un parc d’une symétrie remarquable.
占地二百七十三公顷,在这里您将看到古老的建筑和轴对称的公园。
[旅行的意义]
Je sais que les mots qui portent chance doivent avoir une symétrie gauche-droite et être bien assortis.
我知道要左右对称,吉祥的文字一一对应。
[春节特辑]
L’origine des conventions de conduite est donc une parfaite opportunitée pour les mathématiques de la théorie des jeux et la rupture de symétrie.
因此,驾驶惯例的起源是博弈论数学和对称性突破的一个最好的体现机会。
[地球一分钟]
Harmonie, symétrie, stylisation Les objets et les décors japonisants sont fréquents dans les intérieurs, où ils apportent une touche d'exotisme et de rêve.
谐调,整合和风格。日本的物品和装饰经常出现在画中,笔触流露着异域风情,如梦如幻。
[巴黎奥赛博物馆]
Et quand tu te plies et te déplies par le milieu, là, suivant ton axe de symétrie, tu peux voir que tes deux parties sont égales.
当你居中对折再舒展开来时,沿着对称轴,你可以发现,自己的两部分是相等的。
[基础法语小知识]
Cette rampe a été supprimée depuis, pour la symétrie ; les chevaux crèvent de soif, mais l’œil est flatté.
为了整齐对称,这个斜坡后来被整修不存在了。马儿渴得要死,但人的眼睛是舒适了。
[悲惨世界 Les Misérables 第五部]
Voilà la grenouille coiffée de ces 2 mollusques, dans une symétrie parfaite.
这是上面有这 2 只软体动物的青蛙,完美对称。
[法国TV2台晚间电视新闻 2022年8月合集]
Et bien pas du tout : il n'y a pas de symétrie.
好吧,一点也不:没有对称性。
[Les mots de l'actualité - 2016年合集]
Symétrie du champ et contenu, Ça veut dire que le champ, il a au moins une composante suivant euro, au moins une composante suivant un fil.
[电磁学5-6]
Sous l’aspect de l’implantation, je conseille de disposer les bâtiments parallèlement au Mékong, sans effet de symétrie.
在实施方面,我建议有沿湄公河的建筑物,没有对称的效果。
À des fins de symétrie, serait-il utile d'ajouter à la fin de la phrase « non-prolifération sous tous ses aspects » comme cela est le cas plus tôt dans la phrase?
为了平衡起见,如果在句尾增加“所有方面的不扩散”,是否会有帮助? 先前曾经在句子里出现过。
En effet, le rapport affiche un remarquable dosage d'harmonie, de symétrie et d'attraits logique.
报告确实非常和谐、对称并在逻辑上具有吸引力。
Le mot «faite» a été retenu par souci de symétrie avec la définition des réserves, dans laquelle figurait la même expression.
保留的定义中也出现“所作”一词,为了彼此对称,这里也保留这一用语。
Ce qui s'impose, c'est non seulement une symétrie entre les flux de main-d'œuvre et ceux de capitaux mais aussi une politique plus active en ce qui concerne les flux migratoires, compte tenu de l'effet que la mondialisation a eu sur la répartition de l'emploi.
考虑到全球化影响就业分配的方式,不仅需要实现劳工和资金流动间的平衡,还必须在移民流动方面采取更加肯定的行动。
Quoique sensible au souci de concision dans l'élaboration des règles uniformes, le Groupe de travail a décidé que, puisque l'on définissait le terme “signataire” à l'alinéa e), il convenait de conserver la définition de “prestataire de services de certification” afin d'assurer une symétrie dans la définition des différentes parties impliquées dans le fonctionnement des mécanismes de signature électronique régis par les règles uniformes.
工作组在起草统一规则时非常注意精简词语这个目标。 然而,工作组还是决定,既然(e)款列出了“签字人”概念的定义,那么验证服务提供者的定义也应保留,以确保在统一规则中匀称整齐地列出电子签字计划在操作上所涉及的各当事方的定义。
Le Groupe de travail a été d'avis, toutefois, qu'une telle définition serait utile pour assurer une symétrie dans la définition des diverses parties impliquées dans le fonctionnement des mécanismes de signatures électroniques régis par les règles uniformes.
然而工作组认为,该定义有助于确保在统一规则中匀称整齐地列出电子签字计划在操作上所涉及的各当事方的定义。
Certes, il y a beaucoup à faire à ce niveau-là mais il convient de s'intéresser aussi à l'état de droit international pour maintenir la symétrie entre ces deux dimensions.
大量工作必须在国家一级进行是不争的事实,但需要更多地关注国际法治以维持这两个层面的对称。
De plus, l'attaque mortelle contre les bureaux des Nations Unies à Bagdad a considérablement réduit notre capacité d'action à l'intérieur de l'Iraq, et j'ai insisté pour qu'il y ait une certaine symétrie entre les risques que l'on demandait à l'ONU d'encourir et la substance du rôle qu'il nous était demandé de jouer.
此外,对联合国驻巴格达总部的致命攻击,严重地降低了我们在伊拉克境内的行动能力,因此我坚持认为,在要求联合国接受的风险,与要求我们发挥作用的实质两方面之间,必须有某种程度的相称。
Une telle proposition, injustifiable en droit, aboutirait à bafouer toute règle de symétrie et d'équilibre entre la situation faite au transporteur et au chargeur.
该建议没有任何法律根据,无视在为承运人和托运人创设的情形之间具有对称和均衡性的任何规则。
Pour que la réforme proposée du processus de surveillance du FMI soit efficace, il faudrait que tous les nouveaux mécanismes qui en feraient partie mettent l'accent sur la clarté des objectifs, la symétrie, l'objectivité, l'équité et l'impartialité.
基金组织拟议开展的监测进程改革若要生效,所有新的监测机制都应加强重点、对称、客观、公平和公允。
Pour cette raison, on peut déplorer que la CDI ait opté pour le texte proposé par le Groupe de travail car la recherche de symétrie avec l'article 3 rend l'article 17 un peu confus, en même temps qu'il s'écarte de la position adoptée par la Cour internationale de Justice dans l'affaire Barcelona Traction.
因此,她对委员会倾向于工作组提议的用语表示遗憾,因为与条款草案第3条保持一致的努力导致了第17条出现混乱,并且偏离了国际法院在巴塞罗那电车案中采取的立场。
Le mot « faite » a été retenu par souci de symétrie avec la définition des réserves, dans laquelle figure la même expression.
保留的定义中也出现“所作”一词,为了彼此对称,这里也保留这一用语。
La première de ces réunions, organisée à Arbil, sera une table ronde au cours de laquelle sera examinée la question des symétries et asymétries entre État fédéral et régions; la seconde, qui se tiendra à Bagdad, sera une conférence élargie sur le fédéralisme et la gestion des hydrocarbures.
首先将在埃尔比勒举行一个圆桌讨论会,重点讨论联邦与地区之间平衡和失衡问题,其次将在巴格达召开一个扩大会议,讨论联邦制和油气管理。
Deuxièmement, les questions à débattre ne devraient être ni exclusives, ni limitatives, mais procéder d'une logique de symétrie des préoccupations et des menaces directes ou indirectes à la sécurité tant nationale qu'internationale.
第二,将讨论的问题不应是排外的,也不应是限制性的,而应来自符合逻辑的方法,在关注以及直接或间接的对国家的和国际的安全威胁之间存在对称性。
Comme il est indiqué dans le document de réflexion proposé par la présidence grecque, une telle approche créera un exemple à suivre en termes de symétrie, de synergie et de stratégie.
正如主席国希腊提议的概念文件中所述的那样,这将树立一个对称、协同和战略的典范。
Les inspecteurs ont relevé qu'il y avait une grande symétrie entre les recommandations formulées dans le présent document et les mesures annoncées dans les rapports susmentionnés du Secrétaire général, bien que tous les aspects de ces mesures n'aient pas encore trouvé leur expression concrète.
检查专员指出,本报告所载的建议与秘书长报告所宣布的措施存在着很大的一致性,尽管不是所有的方面都完全相同。
La définition du terme “partie se fiant à la signataire ou au certificat” vise à assurer une symétrie dans la définition des diverses parties impliquées dans le fonctionnement des mécanismes de signature électronique régis par la Loi type (ibid., par. 107).
“依赖方”的定义是为了确保在示范法中匀称整齐地列出电子签字系统在操作上所涉及的各当事方的定义(同上,第107段)。
Cette formulation est symétrique de celle de l'article 62 de la Convention de Vienne sur le droit des traités, relatif au changement fondamental de circonstances, symétrie que l'on retrouve ensuite au paragraphe 1, qui pose deux conditions en l'absence desquelles l'état de nécessité ne peut être invoqué, et au paragraphe 2, qui exclut entièrement deux situations du champ de l'excuse de nécessité.
在这方面,它反映了《维也纳条约法公约》中涉及情况根本变化问题的第62条的用语。 它还反映了第1款在确定不能援引危急情况的两个条件时的用语,也反映了第2款在确定将两种情况完全排除在以危急情况为理由的范围之外时的用语。
Les prétentions à la symétrie dans son programme de travail ont eu pour effet de cimenter l'impasse.
坚持在其工作方案中保持对称的做法巩固了僵局。

 词典释义:
词典释义:
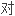 称;匀称
称;匀称 两边
两边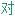 称
称 花坛
花坛
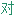 称
称 家具
家具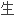 物学】
物学】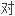 称(性)
称(性)
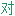 称
称
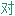 称性
称性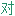 称中心 [轴, 平面]
称中心 [轴, 平面]
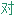 称性
称性 完美
完美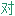 称性
称性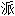
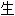 :
: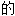 ;
;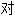 称
称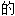 ;n.m.
;n.m.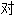 称(性)
称(性)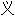 词:
词: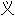 词:
词: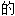 ;
;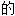 ;
;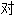 称性;
称性; 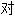 称;
称; 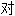
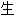
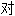 称
称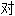 称性
称性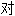 称
称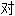 称于
称于 称放大器
称放大器 称轴
称轴 称性
称性 称线
称线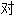 称平面
称平面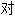 称, 假
称, 假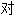 称
称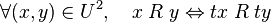
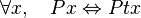
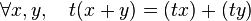
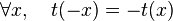
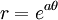
 et
et 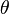 sont les coordonnées polaires d'un point P.
sont les coordonnées polaires d'un point P.
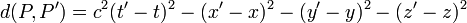
 est la vitesse de la lumière.
est la vitesse de la lumière. est une symétrie si et seulement si pour tous
est une symétrie si et seulement si pour tous 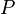 et
et 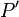

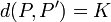 si et seulement si
si et seulement si 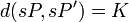 , pour toute constante réelle
, pour toute constante réelle 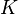 .
.